神经网络 模型表示(一)
神经网络 模型表示
模型表示一
为了构建神经网络模型,我们需要首先思考大脑中的神经网络是怎样的?每一个神经元都可以被认为是一个处理单元/神经核(processing unit/Nucleus),它含有许多输入/树突(input/Dendrite),并且有一个输出/轴突(output/Axon)。神经网络是大量神经元相互链接并通过电脉冲来交流的一个网络。
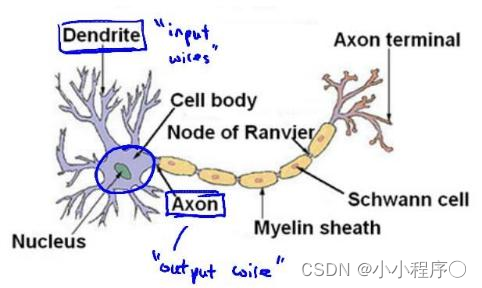
下面是一组神经元的示意图,神经元利用微弱的电流进行沟通。这些弱电流也称作动作电位,其实就是一些微弱的电流。所以如果神经元想要传递一个消息,它就会就通过它的轴突,发送一段微弱电流给其他神经元,这就是轴突。
这里是一条连接到输入神经,或者连接另一个神经元树突的神经,接下来这个神经元接收这条消息,做一些计算,它有可能会反过来将在轴突上的自己的消息传给其他神经元。这就是所有人类思考的模型:我们的神经元把自己的收到的消息进行计算,并向其他神经元传递消息。这也是我们的感觉和肌肉运转的原理。如果你想活动一块肌肉,就会触发一个神经元给你的肌肉发送脉冲,并引起你的肌肉收缩。如果一些感官:比如说眼睛想要给大脑传递一个消息,那么它就像这样发送电脉冲给大脑的。
神经网络模型建立在很多神经元之上,每一个神经元又是一个个学习模型。这些神经元(也叫激活单元,activation unit)采纳一些特征作为输出,并且根据本身的模型提供一个输出。下图是一个以逻辑回归模型作为自身学习模型的神经元示例,在神经网络中,参数又可被成为权重(weight)。

我们设计出了类似于神经元的神经网络,效果如下:
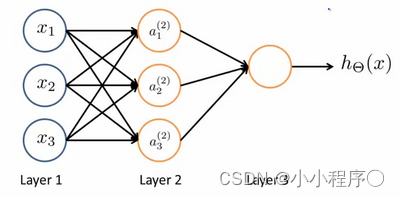
其中 x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x3是输入单元(input units),我们将原始数据输入给它们。
a 1 a_1 a1, a 2 a_2 a2, a 3 a_3 a3是中间单元,它们负责将数据进行处理,然后呈递到下一层。
最后是输出单元,它负责计算 h θ ( x ) {h_\theta}\left( x \right) hθ(x)。
神经网络模型是许多逻辑单元按照不同层级组织起来的网络,每一层的输出变量都是下一层的输入变量。下图为一个3层的神经网络,第一层成为输入层(Input Layer),最后一层称为输出层(Output Layer),中间一层成为隐藏层(Hidden Layers)。我们为每一层都增加一个偏差单位(bias unit)
下面引入一些标记法来帮助描述模型:
a i ( j ) a_{i}^{\left( j \right)} ai(j) 代表第 j j j 层的第 i i i 个激活单元。 θ ( j ) {{\theta }^{\left( j \right)}} θ(j)代表从第 j j j 层映射到第$ j+1$ 层时的权重的矩阵,例如 θ ( 1 ) {{\theta }^{\left( 1 \right)}} θ(1)代表从第一层映射到第二层的权重的矩阵。其尺寸为:以第 j + 1 j+1 j+1层的激活单元数量为行数,以第 j j j 层的激活单元数加一为列数的矩阵。例如:上图所示的神经网络中 θ ( 1 ) {{\theta }^{\left( 1 \right)}} θ(1)的尺寸为 3*4。
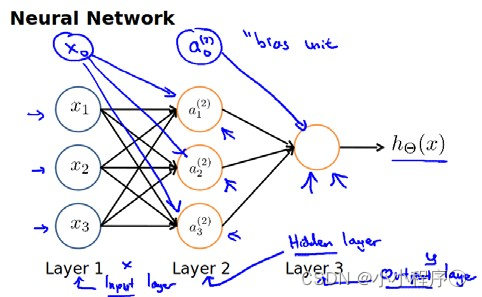
对于上图所示的模型,激活单元和输出分别表达为:
a 1 ( 2 ) = g ( Θ 10 ( 1 ) x 0 + Θ 11 ( 1 ) x 1 + Θ 12 ( 1 ) x 2 + Θ 13 ( 1 ) x 3 ) a_{1}^{(2)}=g(\Theta _{10}^{(1)}{{x}_{0}}+\Theta _{11}^{(1)}{{x}_{1}}+\Theta _{12}^{(1)}{{x}_{2}}+\Theta _{13}^{(1)}{{x}_{3}}) a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3)
a 2 ( 2 ) = g ( Θ 20 ( 1 ) x 0 + Θ 21 ( 1 ) x 1 + Θ 22 ( 1 ) x 2 + Θ 23 ( 1 ) x 3 ) a_{2}^{(2)}=g(\Theta _{20}^{(1)}{{x}_{0}}+\Theta _{21}^{(1)}{{x}_{1}}+\Theta _{22}^{(1)}{{x}_{2}}+\Theta _{23}^{(1)}{{x}_{3}}) a2(2)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3)
a 3 ( 2 ) = g ( Θ 30 ( 1 ) x 0 + Θ 31 ( 1 ) x 1 + Θ 32 ( 1 ) x 2 + Θ 33 ( 1 ) x 3 ) a_{3}^{(2)}=g(\Theta _{30}^{(1)}{{x}_{0}}+\Theta _{31}^{(1)}{{x}_{1}}+\Theta _{32}^{(1)}{{x}_{2}}+\Theta _{33}^{(1)}{{x}_{3}}) a3(2)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3)
h Θ ( x ) = g ( Θ 10 ( 2 ) a 0 ( 2 ) + Θ 11 ( 2 ) a 1 ( 2 ) + Θ 12 ( 2 ) a 2 ( 2 ) + Θ 13 ( 2 ) a 3 ( 2 ) ) {{h}_{\Theta }}(x)=g(\Theta _{10}^{(2)}a_{0}^{(2)}+\Theta _{11}^{(2)}a_{1}^{(2)}+\Theta _{12}^{(2)}a_{2}^{(2)}+\Theta _{13}^{(2)}a_{3}^{(2)}) hΘ(x)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))
上面进行的讨论中只是将特征矩阵中的一行(一个训练实例)喂给了神经网络,我们需要将整个训练集都喂给我们的神经网络算法来学习模型。
我们可以知道:每一个 a a a都是由上一层所有的 x x x和每一个 x x x所对应的决定的。
(我们把这样从左到右的算法称为前向传播算法( FORWARD PROPAGATION ))
把 x x x, θ \theta θ, a a a 分别用矩阵表示:
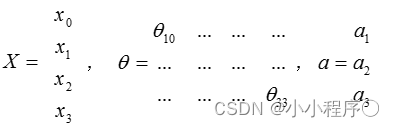
我们可以得到 θ ⋅ X = a \theta \cdot X=a θ⋅X=a 。
相关文章:

神经网络 模型表示(一)
神经网络 模型表示 模型表示一 为了构建神经网络模型,我们需要首先思考大脑中的神经网络是怎样的?每一个神经元都可以被认为是一个处理单元/神经核(processing unit/Nucleus),它含有许多输入/树突(input/…...

【漏洞复现】智跃人力资源管理系统GenerateEntityFromTable.aspx接口存在SQL注入漏洞 附POC
漏洞描述 智跃人力资源管理系统是基于B/S网页端广域网平台,一套考勤系统即可对全国各地多个分公司进行统一管控,成本更低。信息共享更快。跨平台,跨电子设备。智跃人力资源管理系统GenerateEntityFromTable.aspx接口处存在SQL注入漏洞,攻击者可通过该漏洞获取数据库中的信…...
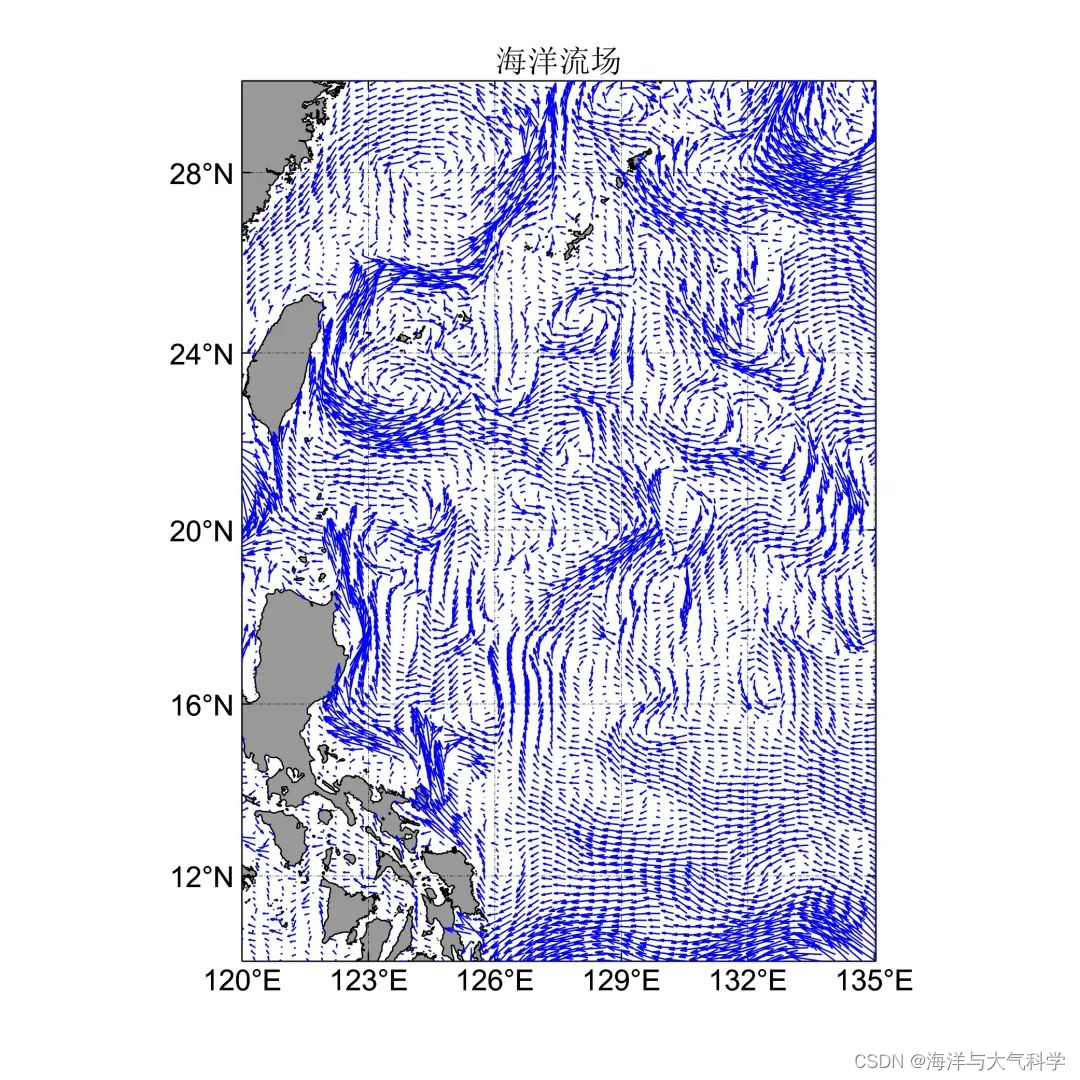
【matlab程序】画海洋流场
【matlab程序】画海洋流场 clear;clc; file ( ‘0227.nc’); latncread(file,‘latitude’); lonncread(file,‘longitude’); uncread(file,‘water_u’); vncread(file,‘water_v’); [x,y]meshgrid(lon,lat); xx’; yy’; interval4; figure (1) set(gcf,‘color’,[1 1 1…...

线性表 力扣67. 二进制求和
题目 67. 二进制求和 翻译 主要思路 核心思路是像竖式计算一样,不过需要将字符串a和b反转后逐位进行二进制计算得到字符串c,最后再将c反转就是答案 逐位计算的时候利用count,在将a和b当前位置数字相加后通过模2来决定字符串c对应位置的数…...

2312skia,13画布包入门
画矶包快速入门 CanvasKit是用比canvasAPI更高级功能集的Skia来绘画元素到canvas中的wasm模块. 最小应用 此例是个最小Canvaskit应用,它为一帧绘画一个圆角矩形.从unpkg.com中提取wasm二进制文件,但你也可自己构建和管理它. <canvas idfoo width300 height300></c…...
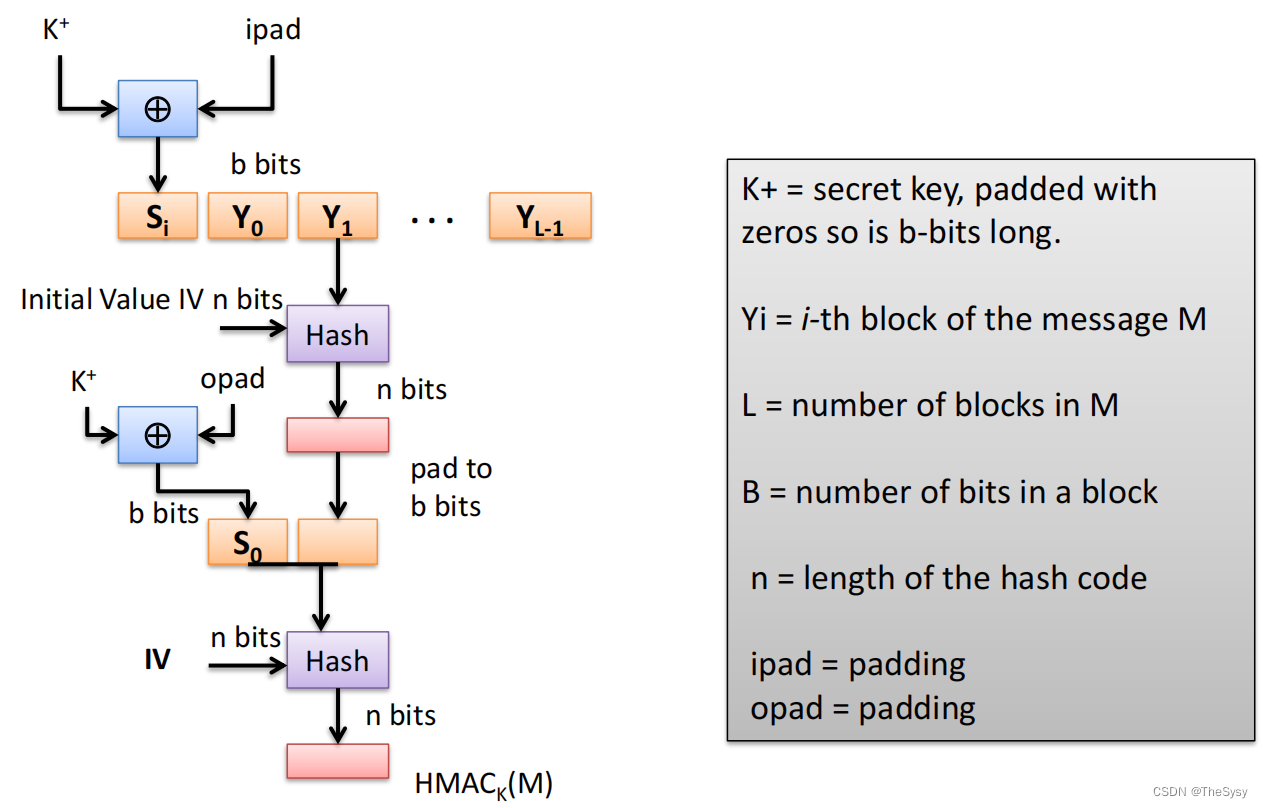
【网络安全技术】消息认证技术
一、哈希函数 1.安全性质 1)抗第一原像攻击(Preimage Resistance) 给定哈希后的值,很难找到哈希前的原消息。这很好理解,需要哈希函数具有单向性。 一个简单的例子就是密码存储系统,用户登录服务器需要…...
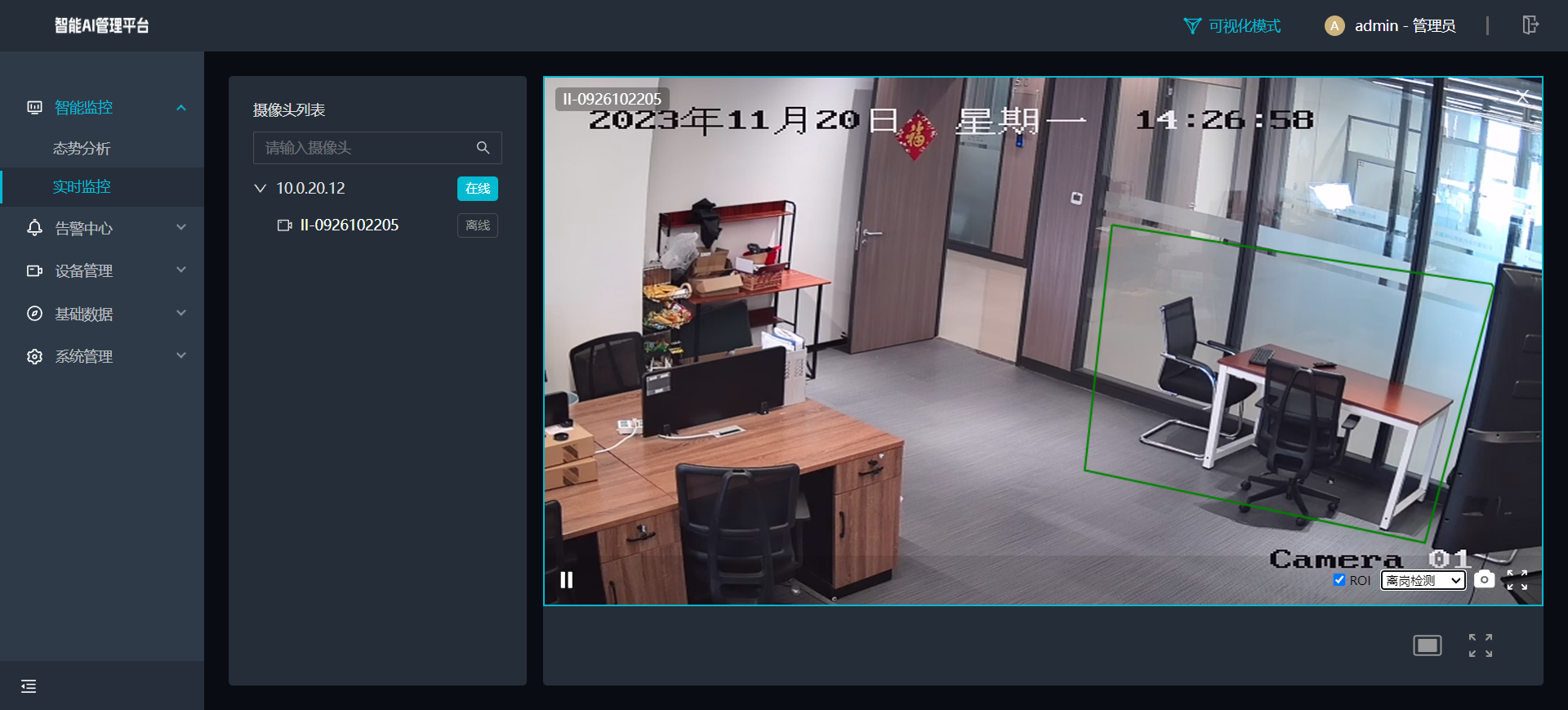
智慧安防三大信息技术:云计算、大数据及人工智能在视频监控EasyCVR中的应用
说到三大信息技术大家都很清楚,指的是云计算、大数据和人工智能,在人工智能(AI)快速发展的当下,例如常见的大数据分析、人工智能芯片生产的智能机器人等等,在工作、生活、教育、金融、科技、工业、农业、娱…...
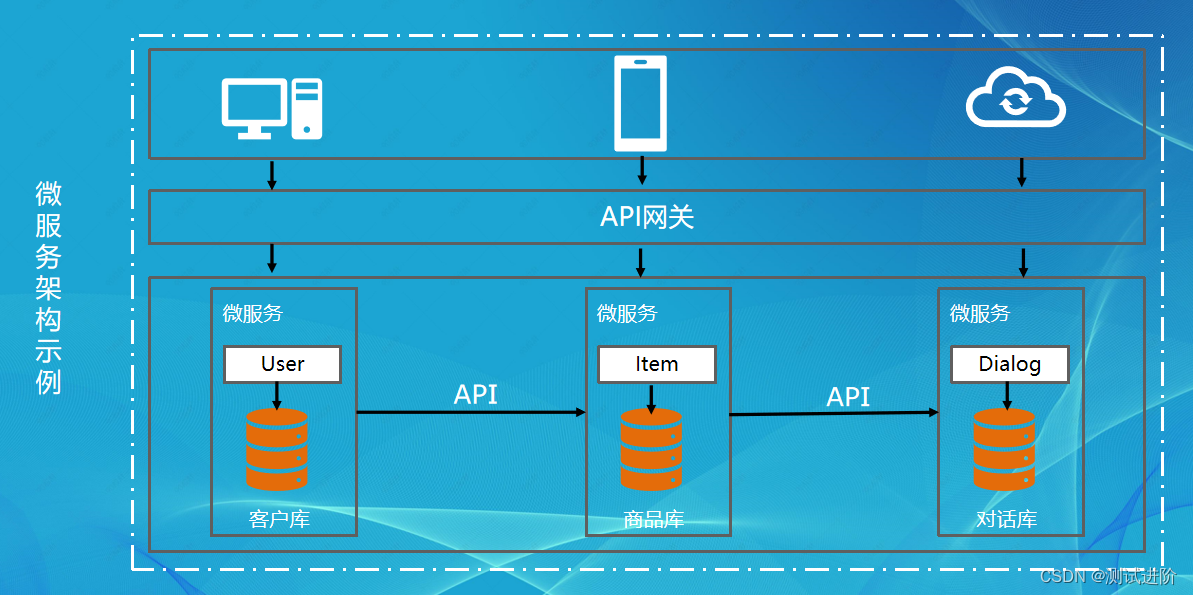
接口测试基础知识
一、接口测试简介 什么是接口测试? 接口测试是测试系统组件间接口的一种测试,主要用于检测外部系统与系统之间以及内部各个子系统之间的交互点。 测试的重点: 检查数据的交换,传递和控制管理过程;检查系统间的相互…...

C++多线程之通过成员函数作为线程入口
说明: 通过类里面的函数作为线程入口,我个人难理解的地方在于给线程传递参数的时候,怎么找到Main函数。后面会做分析。 首先创建类:创建MyThread类,其中公有函数Main作为入口。这个类的传教比较简单,成员…...
)
word、excel文件转PDF(documents4j方式,简单)
1 documents4j方式 引入pom <dependency><groupId>com.documents4j</groupId><artifactId>documents4j-local</artifactId><version>1.1.12</version></dependency><dependency><groupId>com.documents4j</g…...
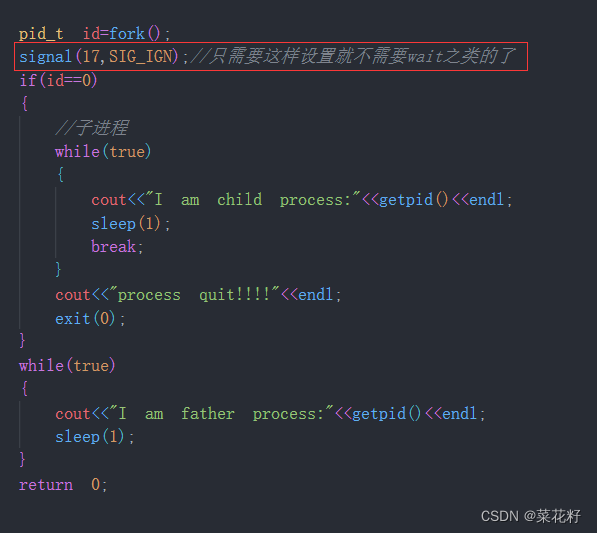
【Linux】:信号(三)捕捉
信号捕捉 一.sigaction1.基本使用2.sa_mask字段 二.可重入函数三.volatile四.SIGCHLD信号 承接上文 果信号的处理动作是用户自定义函数,在信号递达时就调用这个函数,这称为捕捉信号。由于信号处理函数的代码是在用户空间的,处理过程比较复杂,举例如下: 用户程序注册了SIGQUIT信…...
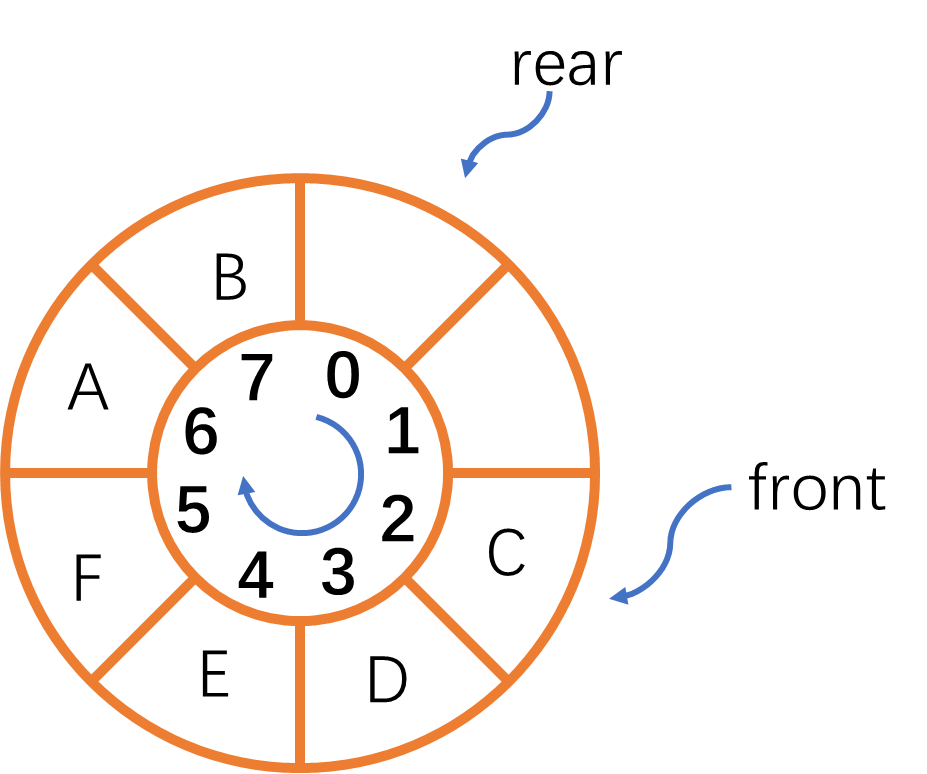
数据结构 / 队列 / 循环队列 / 概念
1. 定义 为充分利用向量空间,克服假溢出现象的方法是:将向量空间想象为一个首尾相接的圆环,并称这种向量为循环向量。存储在其中的队列称为循环队列(Circular Queue)。循环队列是把顺序队列首尾相连,把存储…...
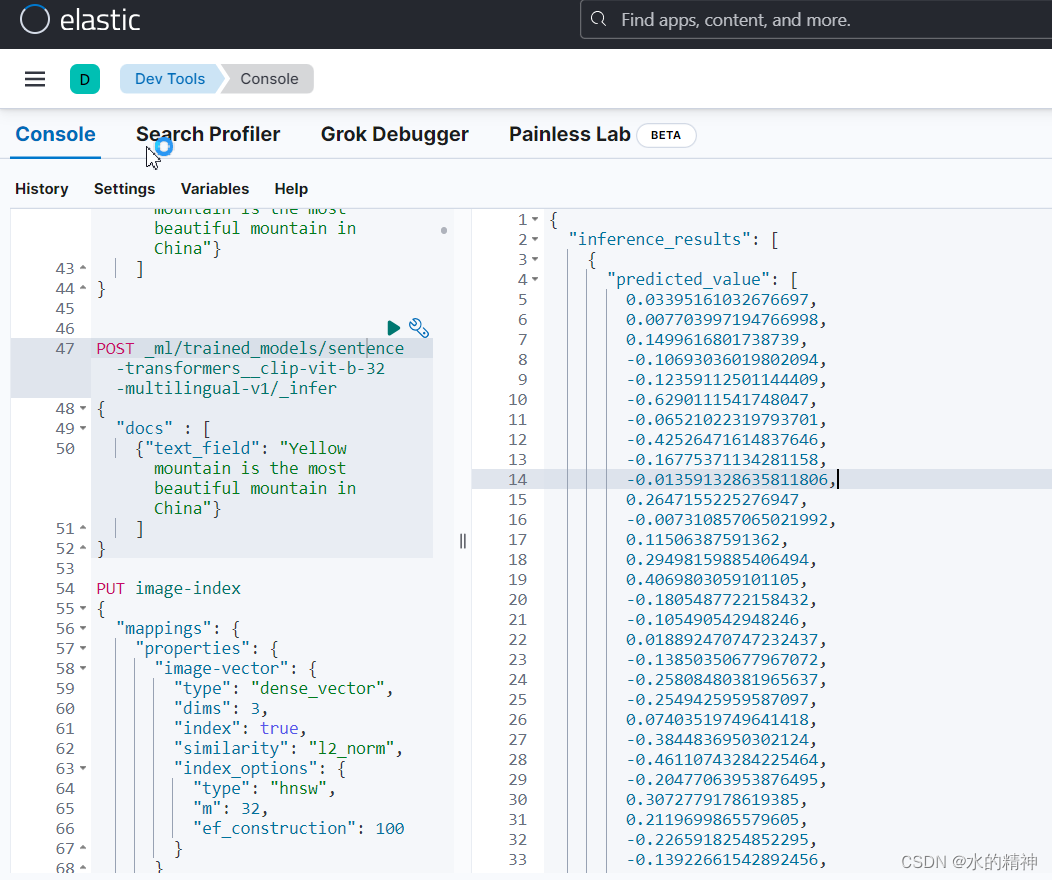
elasticsearch 内网下如何以离线的方式上传任意的huggingFace上的NLP模型(国内闭坑指南)
es自2020年的8.x版本以来,就提供了机器学习的能力。我们可以使用es官方提供的工具eland,将hugging face上的NLP模型,上传到es集群中。利用es的机器学习模块,来运维部署管理模型。配合es的管道处理,来更加便捷的处理数据…...

vue中中的动画组件使用及如何在vue中使用animate.css
“< Transition >” 是一个内置组件,这意味着它在任意别的组件中都可以被使用,无需注册。它可以将进入和离开动画应用到通过默认插槽传递给它的元素或组件上。进入或离开可以由以下的条件之一触发: 由 v-if 所触发的切换由 v-show 所触…...
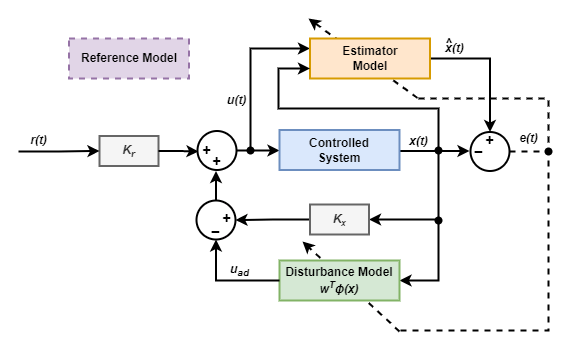
MATLAB 模型参考自适应控制 - Model Reference Adaptive Control
系列文章目录 文章目录 系列文章目录前言一、参考模型二、扰动与不确定性模型三、直接 MRAC名义模型参数更新间接 MRAC估计器模型和控制器增益参数更新学习修正参考文献 前言 模型参考自适应控制模块计算控制动作,使不确定的受控系统跟踪给定参考被控对象模型的行为…...

【如何用批处理文件实现自动编译Keil工程和C# Visual Studio工程】
如何用批处理文件实现自动编译Keil工程和C# Visual Studio工程 写个Bat 批处理文件,现自动编译Keil工程和C# Visual Studio工程。这样可以结合Python 实现复杂的操作。 编译Keil工程: echo off set UVC:\Keil_v5\UV4\UV4.exe set UV_PRO_PATHD:\worksp…...

大模型的实践应用11-“书生”通用大模型的搭建与模型代码详细介绍,以及快速使用方法
大家好,我是微学AI,今天给大家介绍一下大模型的实践应用11-“书生”通用大模型的搭建与模型代码详细介绍,以及快速使用方法。“书生” 通用大模型是上海人工智能实验室研制的大模型,并且已经开源了“书生浦语”大模型70亿参数的轻量级版本InternLM-7B。InternLM-7B模型主要…...

【开发PaaS】基于Postgresql的开发平台Supabase
Supadase是开源的。我们选择可扩展的开源工具,使其易于使用。 Supadase不是Firebase的1对1映射。虽然我们正在构建Firebase提供的许多功能,但我们不会以同样的方式进行: 我们的技术选择大不相同;我们使用的一切都是开源的&#…...

前端开启gzip优化页面加载速度
生成gizp的打包资源,可以优化页面加载速度 打包的时候开启gzip可以很大程度减少包的大小,页面大小可以变为原来的30%甚至更小,非常适合线上部署, 但还记得需要服务端支持 1、前端配置compression-webpack-plugin 先安装:npm install compres…...

用Java写一个俄罗斯方块
目录 游戏规则 小方块类:Cell 七种图形类:I、J、L、O、S、T、Z J L O S T Z 俄罗斯方块游戏主类:Tetris 效果展示 游戏规则 由小方块组成的不同形状的板块陆续从屏幕上方落下来,玩家通过调整板块的位置和方向,使它…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...
