【如何用批处理文件实现自动编译Keil工程和C# Visual Studio工程】
如何用批处理文件实现自动编译Keil工程和C# Visual Studio工程
写个Bat 批处理文件，现自动编译Keil工程和C# Visual Studio工程。这样可以结合Python 实现复杂的操作。
编译Keil工程：
@echo off
set UV=C:\Keil_v5\UV4\UV4.exe
set UV_PRO_PATH=D:\workspace\3-iot\3_iot_framework\vender\At32f403\MDK_v5\Template.uvprojx
echo Init building 3_iot_framework...
echo .>build_log.txt%UV% -r %UV_PRO_PATH% -t "3-IOT-Framework" -o .\build_log.txt
C:\Keil_v5\ARM\ARMCC\bin\fromelf.exe --bin D:\workspace\3-iot\3_iot_framework\vender\At32f403\MDK_v5\Objects\1100005070601T.axf -o D:\workspace\3-iot\3_iot_framework\vender\At32f403\Objects\1100005070601T.bintype build_log.txt
echo Done.
编译C# Visual Studio工程：
C:“/Program Files (x86)/Microsoft Visual Studio/2019/Community/MSBuild/Current/Bin/MSBuild.exe” D:\workspace\BGC_Tools\BGC_Tools\BGC_Tools.sln /p:Configuration=Debug
这样可以结合Python 实现复杂的操作。
B站视频连接：
做了个工具自动调用Python生产pubkey和.h文件和.cs的c#文件，调用keil和visual studio编译arm和c#的工程，在文件拷贝用户目录。
抖音也可以搜索柔贝特三哥看视频哦。
相关文章：
【如何用批处理文件实现自动编译Keil工程和C# Visual Studio工程】
如何用批处理文件实现自动编译Keil工程和C# Visual Studio工程 写个Bat 批处理文件，现自动编译Keil工程和C# Visual Studio工程。这样可以结合Python 实现复杂的操作。 编译Keil工程： echo off set UVC:\Keil_v5\UV4\UV4.exe set UV_PRO_PATHD:\worksp…...
大模型的实践应用11-“书生”通用大模型的搭建与模型代码详细介绍，以及快速使用方法
大家好，我是微学AI，今天给大家介绍一下大模型的实践应用11-“书生”通用大模型的搭建与模型代码详细介绍，以及快速使用方法。“书生” 通用大模型是上海人工智能实验室研制的大模型，并且已经开源了“书生浦语”大模型70亿参数的轻量级版本InternLM-7B。InternLM-7B模型主要…...
【开发PaaS】基于Postgresql的开发平台Supabase
Supadase是开源的。我们选择可扩展的开源工具，使其易于使用。 Supadase不是Firebase的1对1映射。虽然我们正在构建Firebase提供的许多功能，但我们不会以同样的方式进行： 我们的技术选择大不相同；我们使用的一切都是开源的&#…...
前端开启gzip优化页面加载速度
生成gizp的打包资源，可以优化页面加载速度 打包的时候开启gzip可以很大程度减少包的大小，页面大小可以变为原来的30%甚至更小,非常适合线上部署, 但还记得需要服务端支持 1、前端配置compression-webpack-plugin 先安装：npm install compres…...
用Java写一个俄罗斯方块
目录 游戏规则 小方块类：Cell 七种图形类：I、J、L、O、S、T、Z J L O S T Z 俄罗斯方块游戏主类：Tetris 效果展示 游戏规则 由小方块组成的不同形状的板块陆续从屏幕上方落下来，玩家通过调整板块的位置和方向，使它…...
应用于智慧金融的AI边缘计算盒子+AI算法软硬一体化方案
传统金融营业厅存在运营管理模式落后、资源投放不平衡、从业人员培训效果不达预期、客户体验割裂等普遍现象； 部署英码数字金融解决方案，将助力企业从传统金融模式快速向数字金融模式转变，可针对每一个客户定制个性化“一对一”服务ÿ…...
目标检测——Faster R-CNN算法解读
论文：Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks 作者：Shaoqing Ren, Kaiming He, Ross Girshick, and Jian Sun 链接：https://arxiv.org/abs/1506.01497 代码：https://github.com/rbgirsh…...
Wireshark （一）安装入门 —— 软件介绍
文章目录 Wireshark是什么？为什么要使用Wireshark？相关网络分析工具软件对比 Wireshark是什么？ Wireshark是一种开源网络协议分析器，它可以捕获和分析网络中传输的数据包。 用户可以使用Wireshark来诊断网络问题、了解网络协议的…...
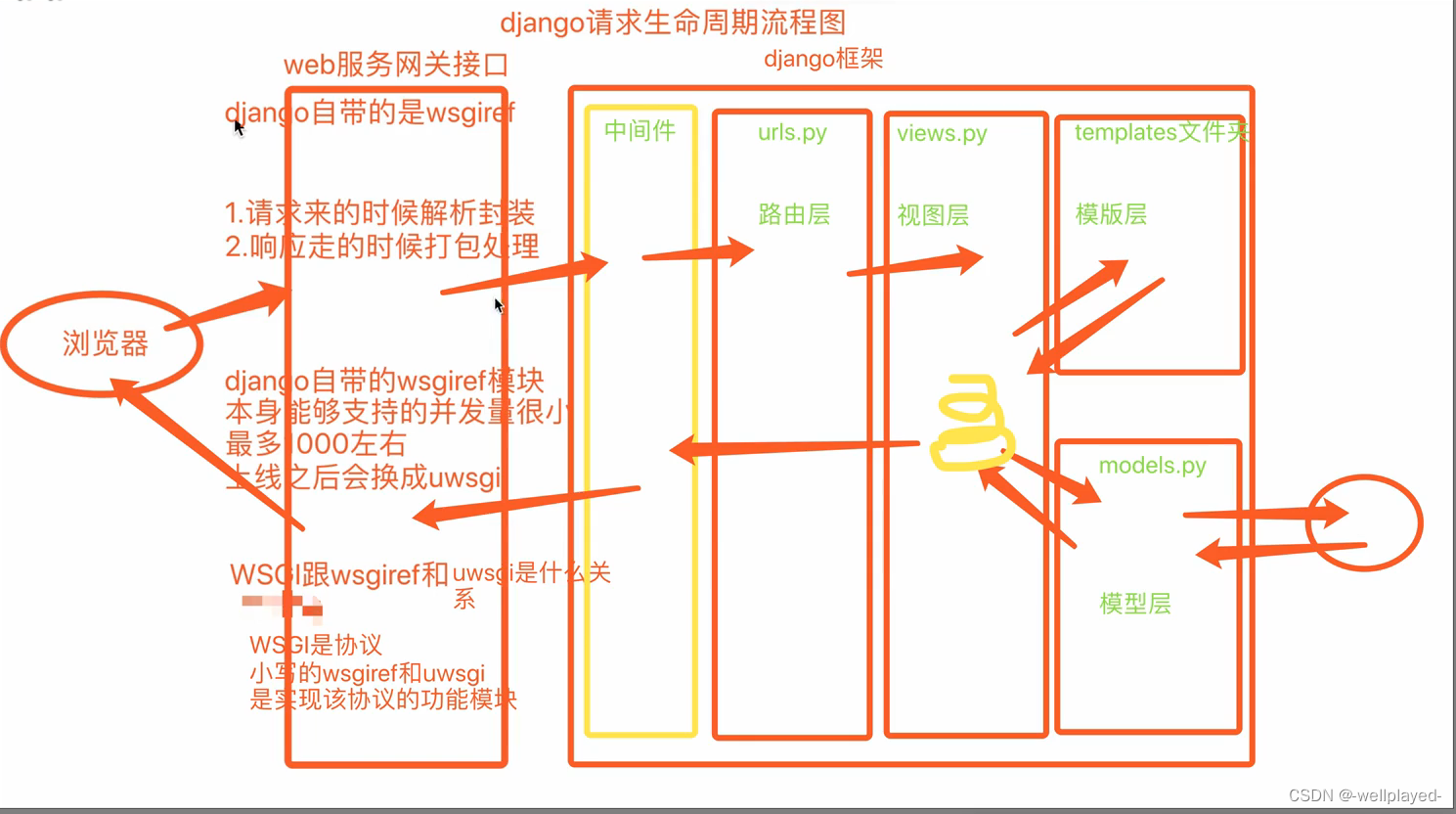
Web框架与Django路由层
Web框架 一 web框架 Web框架（Web framework）是一种开发框架，用来支持动态网站、网络应用和网络服务的开发。这大多数的web框架提供了一套开发和部署网站的方式，也为web行为提供了一套通用的方法。web框架已经实现了很多功能&…...
什么是CAS, 什么是AQS
文章目录 什么是CAS, 什么是AQSCASAQS 什么是CAS, 什么是AQS CAS AQS AQS 全称是AbstractQueuedSynchronizer， 是juc 下一个核心的抽象类，用于构建各种同步器和锁 比如我们熟悉的 ReentrantLock、ReadWriteLock、CountDownLatch等等是基于AQS. 首先在…...
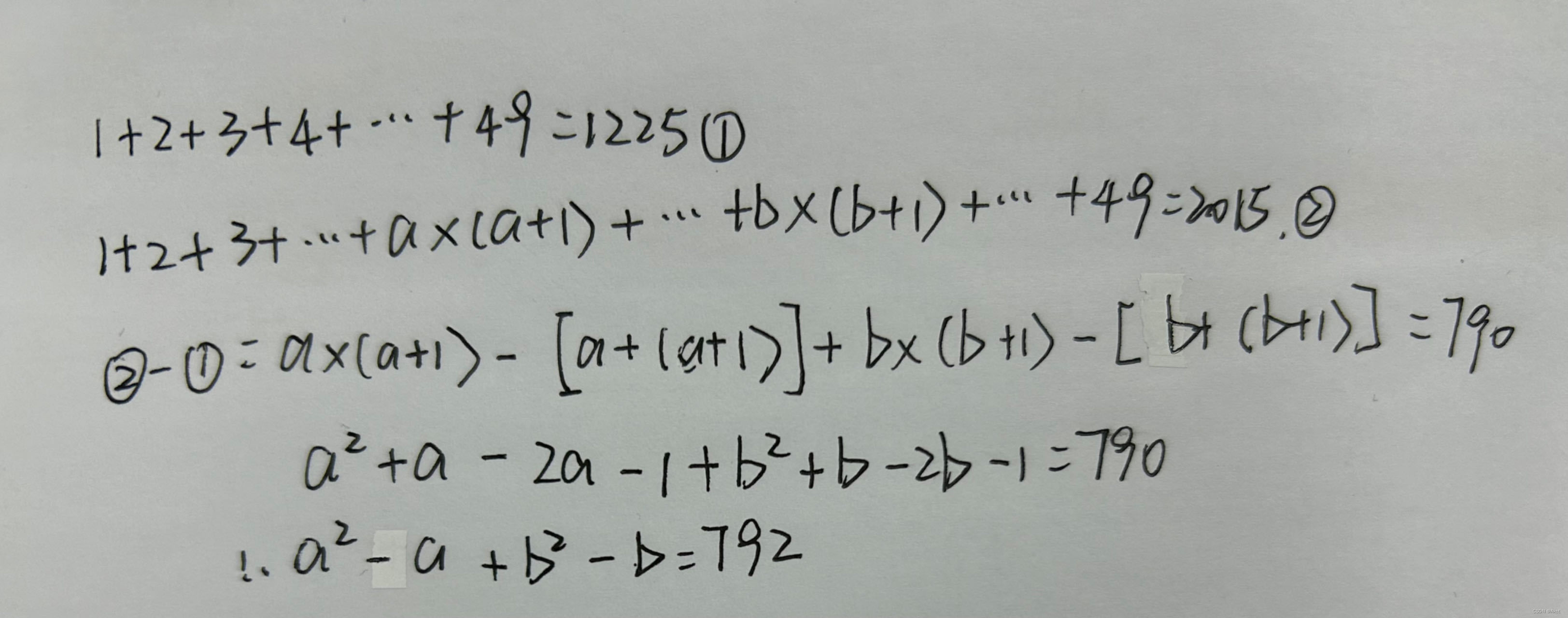
蓝桥杯每日一题2023.12.1
题目描述 蓝桥杯大赛历届真题 - C 语言 B 组 - 蓝桥云课 (lanqiao.cn) 题目分析 对于此题目而言思路较为重要，实际可以转化为求两个数字对应的操作，输出最前面的数字即可 #include<bits/stdc.h> using namespace std; int main() {for(int i 1…...
正则表达式从放弃到入门（1）：“正则表达式”是什么？
正则表达式从放弃到入门（1）：“正则表达式”是什么？ 本博文转载自 这是一篇”正则表达式”扫盲贴，如果你还不理解什么是正则表达式，看这篇文章就对了。 如果你已经掌握了”正则表达式”，就不用再…...
SQL解惑 - 谜题2
文章目录 一、谜题描述二、分析三、答案四、总结 一、谜题描述 创建一个记录雇员缺勤率的数据库。使用的表结构如下：Absenteeism 主键：PRIMARY KEY (emp_id, absent_date) 字段名字段类型字段中文名字段描述emp_idINTERGER雇员id-absent_dateSTRING缺勤…...
FWT+高维前缀和：Gym - 103202M
https://vj.imken.moe/contest/597216#problem/F 考虑两个人的集合分别为 i , j i,j i,j，那么我们令 f ( i ⊗ j ) f(i\otimes j) f(i⊗j)，其中 f ( s ) f(s) f(s) 表示两个人不同集合恰好为 s s s，显然 f ( s ) f(s) f(s) 可以FWT求…...
【C++】string类的接口综合运用
目录 介绍： 一，string对象的构建 二，string类对象的容量操作 介绍： string容器我们之前已经粗略了解了基本增添、修改、删除、插入等基本功能，这里就不再做过多说明，接下来我们全面并详细…...
分布式ID生成框架Leaf升级踩坑
背景： 在项目中需要一个统一的拿单号等唯一ID的服务，就想起了之前用到的leaf，但是因为项目要求，leaf的版本不符合，需要做一些升级 项目地址：https://github.com/Meituan-Dianping/Leaf 升级点࿱…...
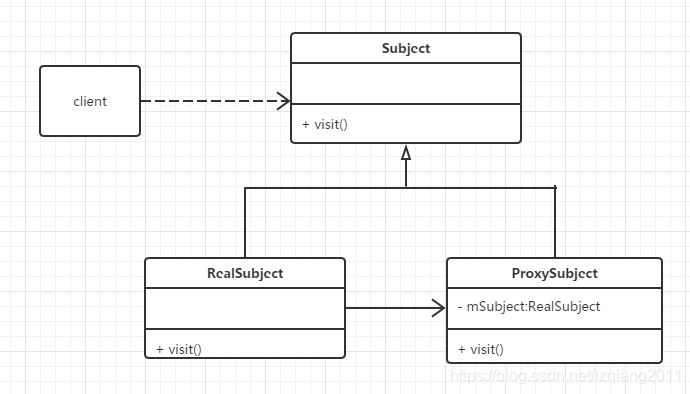
常用的设计模式
文章目录 常用的设计模式：一、单例模式3、懒汉式 - 懒汉式非线程安全4、饿汉式 - 线程安全5、懒汉式和饿汉式区别6、双重检查锁定7、应用场景 二、工厂模式1、简单工厂模式2、工厂模式3、抽象工厂4、总结 三、代理模式1、静态代理2、动态代理jdk自带动态代理 3、Cgl…...
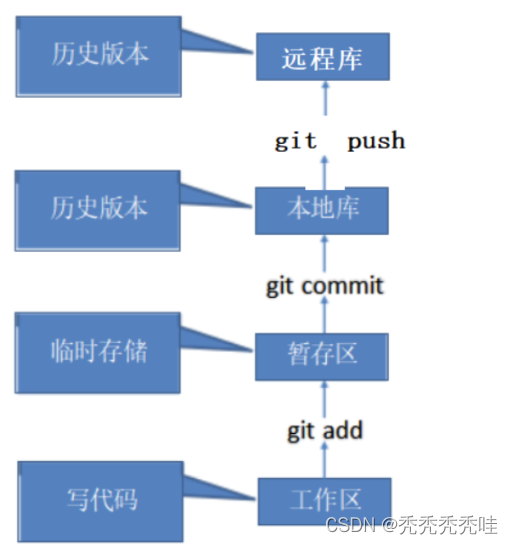
git的相关实用命令
参看文章：https://blog.csdn.net/qq_21688871/article/details/130158888 http://www.mobiletrain.org/about/BBS/159885.html 1、git commit后，但发现文件有误，不想push(提交到本地库，回退到暂存区） git reset --sof…...
【使用`model.status`来获取gurobi求解过程中的模型状态】
在Gurobi中，你可以使用model.status来获取求解过程中的模型状态。可以使用了model.status来检查模型是否找到最优解。模型状态是一个Gurobi的常量，表示了求解过程中的不同状态。 以下是一些常见的模型状态： GRB.OPTIMAL: 最优解被找到。GRB…...
【UGUI】Unity教程：实现物品的拖拽功能
大家好，今天，我们将一起学习如何在Unity中实现物品的拖拽功能。这是一个非常实用的技能，无论你是在制作RPG游戏的背包系统，还是在制作策略游戏的建筑放置功能，都会用到这个技能。那么，让我们开始吧…...
vscode里如何用git
打开vs终端执行如下： 1 初始化 Git 仓库（如果尚未初始化） git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...
MySQL 8.0 OCP 英文题库解析（十三）
Oracle 为庆祝 MySQL 30 周年，截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始，将英文题库免费公布出来，并进行解析，帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...
成都鼎讯硬核科技！雷达目标与干扰模拟器，以卓越性能制胜电磁频谱战
在现代战争中，电磁频谱已成为继陆、海、空、天之后的 “第五维战场”，雷达作为电磁频谱领域的关键装备，其干扰与抗干扰能力的较量，直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器，凭借数字射…...
【Oracle】分区表
个人主页：Guiat 归属专栏：Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
AI病理诊断七剑下天山，医疗未来触手可及
一、病理诊断困局：刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断"，医生需通过显微镜观察组织切片，在细胞迷宫中捕捉癌变信号。某省病理质控报告显示，基层医院误诊率达12%-15%，专家会诊…...
力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...
R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中，科研绘图是必不可少的，一张好看的图形会是文章很大的加分项。 为了便于使用，本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中，获取方式： R 语言科研绘图模板 --- sciRplothttps://mp.…...
Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上，对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...