FWT+高维前缀和:Gym - 103202M
https://vj.imken.moe/contest/597216#problem/F
考虑两个人的集合分别为 i , j i,j i,j,那么我们令 f ( i ⊗ j ) + + f(i\otimes j)++ f(i⊗j)++,其中 f ( s ) f(s) f(s) 表示两个人不同集合恰好为 s s s,显然 f ( s ) f(s) f(s) 可以FWT求。
假设 g ( t ) g(t) g(t) 表示选集合为 t t t 有多少个不同的对数,显然有 g ( t ) = ∑ s & j ≠ ∅ f ( s ) = n ( n − 1 ) 2 − ∑ s ⊆ U − t f ( s ) g(t)=\sum_{s\& j\neq \empty}f(s)=\frac {n(n-1)}2-\sum_{s\subseteq U-t}f(s) g(t)=∑s&j=∅f(s)=2n(n−1)−∑s⊆U−tf(s),因此我们对 f f f 做一遍高维前缀和即可。
#include<bits/stdc++.h>
using namespace std;
#ifdef LOCAL#define debug(...) fprintf(stdout, ##__VA_ARGS__)
#else#define debug(...) void(0)
#endif
#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
#define fi first
#define se second
//srand(time(0));
#define N 2000010
//#define M
//#define mo
int n, m, i, j, k, T;
int g[N], a[N], ans;
char str[N]; struct FWT {int f[N], n, o, i, j, k; void XOR(int x) {for(k=1, o=2; o<=n; o<<=1, k<<=1) {for(i=0; i<n; i+=o) for(j=0; j<k; ++j) {f[i+j]+=f[i+j+k]; f[i+j+k]=f[i+j]-2*f[i+j+k]; if(x==-1) f[i+j]/=2, f[i+j+k]/=2; }}}void Mul() {for(i=0; i<n; ++i) f[i]*=f[i]; }void work(int p) {f[0]-=p; for(i=0; i<n; ++i) f[i]/=2; }
}fwt;signed main()
{#ifdef LOCALfreopen("in.txt", "r", stdin);freopen("out.txt", "w", stdout);#endif
// T=read();
// while(T--) {
//
// }n=read(); m=read(); k=read(); fwt.n=(1<<m); for(i=1; i<=n; ++i) {scanf("%s", str+1); for(j=1; j<=m; ++j) if(str[j]=='B') a[i]|=(1<<j-1); fwt.f[a[i]]++; }fwt.XOR(1); fwt.Mul(); fwt.XOR(-1); fwt.work(n); for(i=0; i<(1<<m); ++i) g[i]=fwt.f[i]; for(i=0; i<(1<<m); ++i) debug("%lld ", g[i]); debug("\n"); for(j=0; j<m; ++j)for(i=0; i<(1<<m); ++i) if(i&(1<<j)) g[i]+=g[i-(1<<j)]; for(i=0; i<(1<<m); ++i) debug("%lld ", g[i]); debug("\n"); for(i=0; i<(1<<m); ++i) if(i<(1<<m)-i) swap(g[i], g[(1<<m)-1-i]); for(i=0; i<(1<<m); ++i) debug("%lld ", g[i]); debug("\n"); for(i=1; i<(1<<m); ++i) g[i]=n*(n-1)/2-g[i]; for(i=1; i<(1<<m); ++i) if(g[i]>=k) ++ans; printf("%lld", ans); return 0;
}相关文章:

FWT+高维前缀和:Gym - 103202M
https://vj.imken.moe/contest/597216#problem/F 考虑两个人的集合分别为 i , j i,j i,j,那么我们令 f ( i ⊗ j ) f(i\otimes j) f(i⊗j),其中 f ( s ) f(s) f(s) 表示两个人不同集合恰好为 s s s,显然 f ( s ) f(s) f(s) 可以FWT求…...

【C++】string类的接口综合运用
目录 介绍: 一,string对象的构建 二,string类对象的容量操作 介绍: string容器我们之前已经粗略了解了基本增添、修改、删除、插入等基本功能,这里就不再做过多说明,接下来我们全面并详细…...

分布式ID生成框架Leaf升级踩坑
背景: 在项目中需要一个统一的拿单号等唯一ID的服务,就想起了之前用到的leaf,但是因为项目要求,leaf的版本不符合,需要做一些升级 项目地址:https://github.com/Meituan-Dianping/Leaf 升级点࿱…...
常用的设计模式
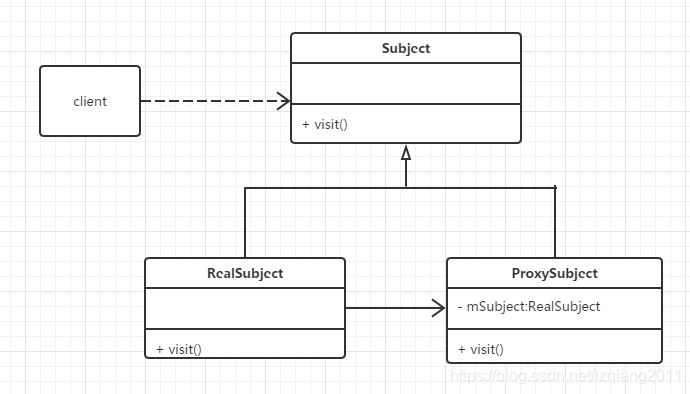
文章目录 常用的设计模式:一、单例模式3、懒汉式 - 懒汉式非线程安全4、饿汉式 - 线程安全5、懒汉式和饿汉式区别6、双重检查锁定7、应用场景 二、工厂模式1、简单工厂模式2、工厂模式3、抽象工厂4、总结 三、代理模式1、静态代理2、动态代理jdk自带动态代理 3、Cgl…...
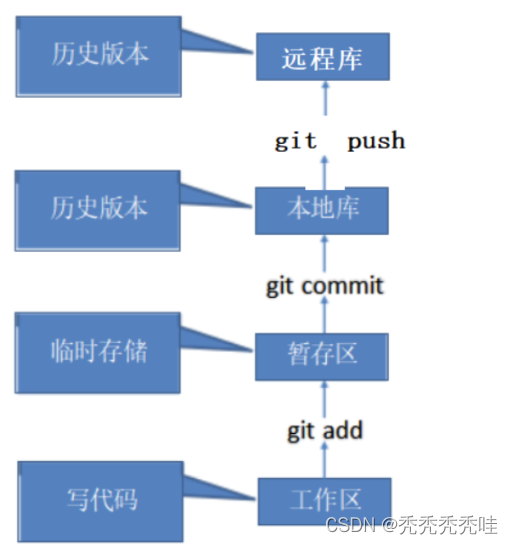
git的相关实用命令
参看文章:https://blog.csdn.net/qq_21688871/article/details/130158888 http://www.mobiletrain.org/about/BBS/159885.html 1、git commit后,但发现文件有误,不想push(提交到本地库,回退到暂存区) git reset --sof…...

【使用`model.status`来获取gurobi求解过程中的模型状态】
在Gurobi中,你可以使用model.status来获取求解过程中的模型状态。可以使用了model.status来检查模型是否找到最优解。模型状态是一个Gurobi的常量,表示了求解过程中的不同状态。 以下是一些常见的模型状态: GRB.OPTIMAL: 最优解被找到。GRB…...

【UGUI】Unity教程:实现物品的拖拽功能
大家好,今天,我们将一起学习如何在Unity中实现物品的拖拽功能。这是一个非常实用的技能,无论你是在制作RPG游戏的背包系统,还是在制作策略游戏的建筑放置功能,都会用到这个技能。那么,让我们开始吧…...

【奇淫技巧】两数交换
【奇淫技巧】两数交换 临时变量法:借助中间变量加减法:不使用中间变量异或法:不使用中间变量语法糖:某些编程语言支持交换语法糖借助函数,不交换 前提:待交换的两个元素,分别用a,b表示…...

Java核心知识点整理大全26-笔记
目录 27. Storm 7.1.1. 概念 27.1.1. 集群架构 27.1.1.1. Nimbus(master-代码分发给 Supervisor) 27.1.1.2. Supervisor(slave-管理 Worker 进程的启动和终止) 27.1.1.3. Worker(具体处理组件逻辑的进程ÿ…...

“上云”还是“下云”?探云计算的下一站未来!
引言 10 月 27 日,X(原Twitter)工程技术发布帖子称,在过去的一年里,技术团队优化了 X 的云服务使用方式,着手将更多工作负载迁往本地基础设施。这一转变使 X 每月的云成本降低了 60%。所有媒体、Blob 存储均…...

Linux中top命令输出日志分析?
以下是对输出的各部分的解释: 09:54:34:系统当前时间。up 161 days, 2:08:系统已经运行了161天2小时8分钟。5 users:有5个用户登录系统。load average: 0.13, 0.08, 0.05:系统的1分钟、5分钟、15分钟的平均负载。负载…...

执行栈和执行上下文
前端面试大全JavaScript执行栈和执行上下文 🌟经典真题 🌟执行上下文 🌟栈数据结构 🌟执行上下文生命周期 🌟真题解答 🌟总结 🌟经典真题 谈谈你对 JavaScript 执行上下文栈理解 &#…...
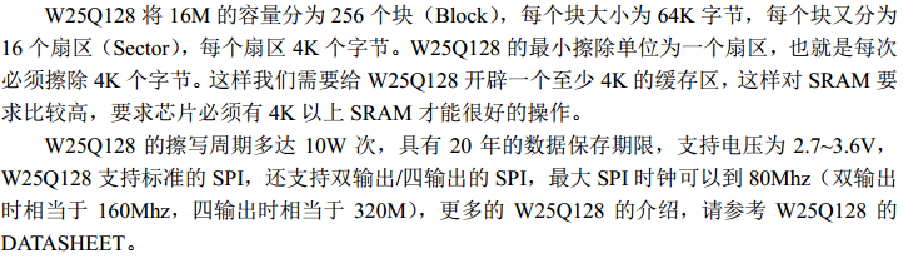
7、单片机与W25Q128(FLASH)的通讯(SPI)实验(STM32F407)
SPI接口简介 SPI 是英语Serial Peripheral interface的缩写,顾名思义就是串行外围设备接口。是Motorola首先在其MC68HCXX系列处理器上定义的。 SPI,是一种高速的,全双工,同步的通信总线,并且在芯片的管脚上只占用四根…...
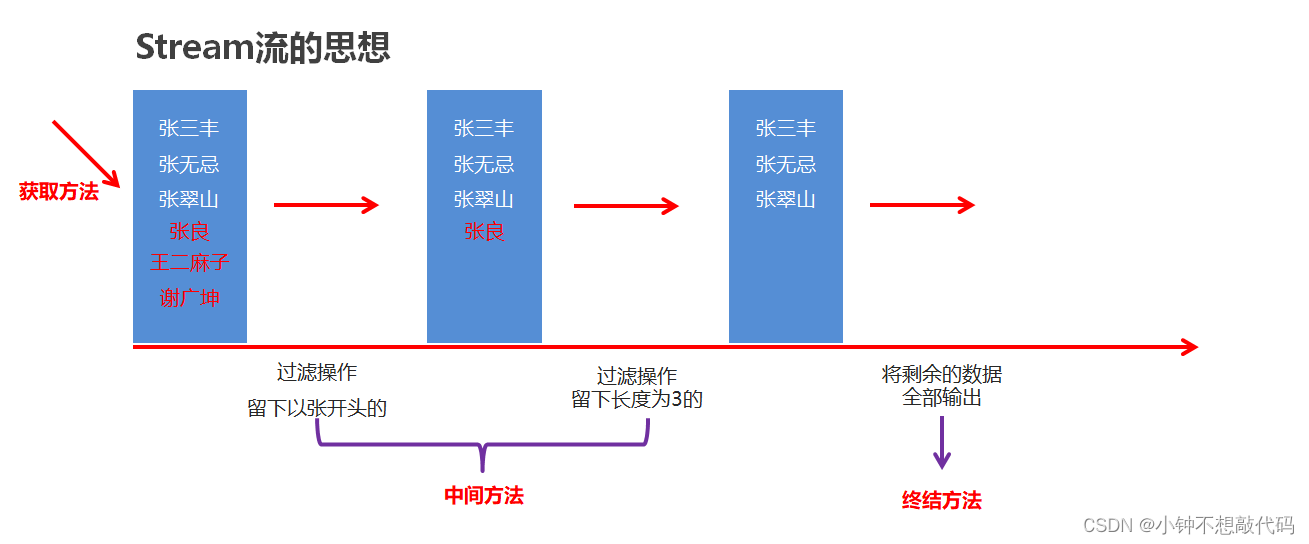
stream流和方法引用
1.Stream流 1.1体验Stream流【理解】 案例需求 按照下面的要求完成集合的创建和遍历 创建一个集合,存储多个字符串元素把集合中所有以"张"开头的元素存储到一个新的集合把"张"开头的集合中的长度为3的元素存储到一个新的集合遍历上一步得到的集…...
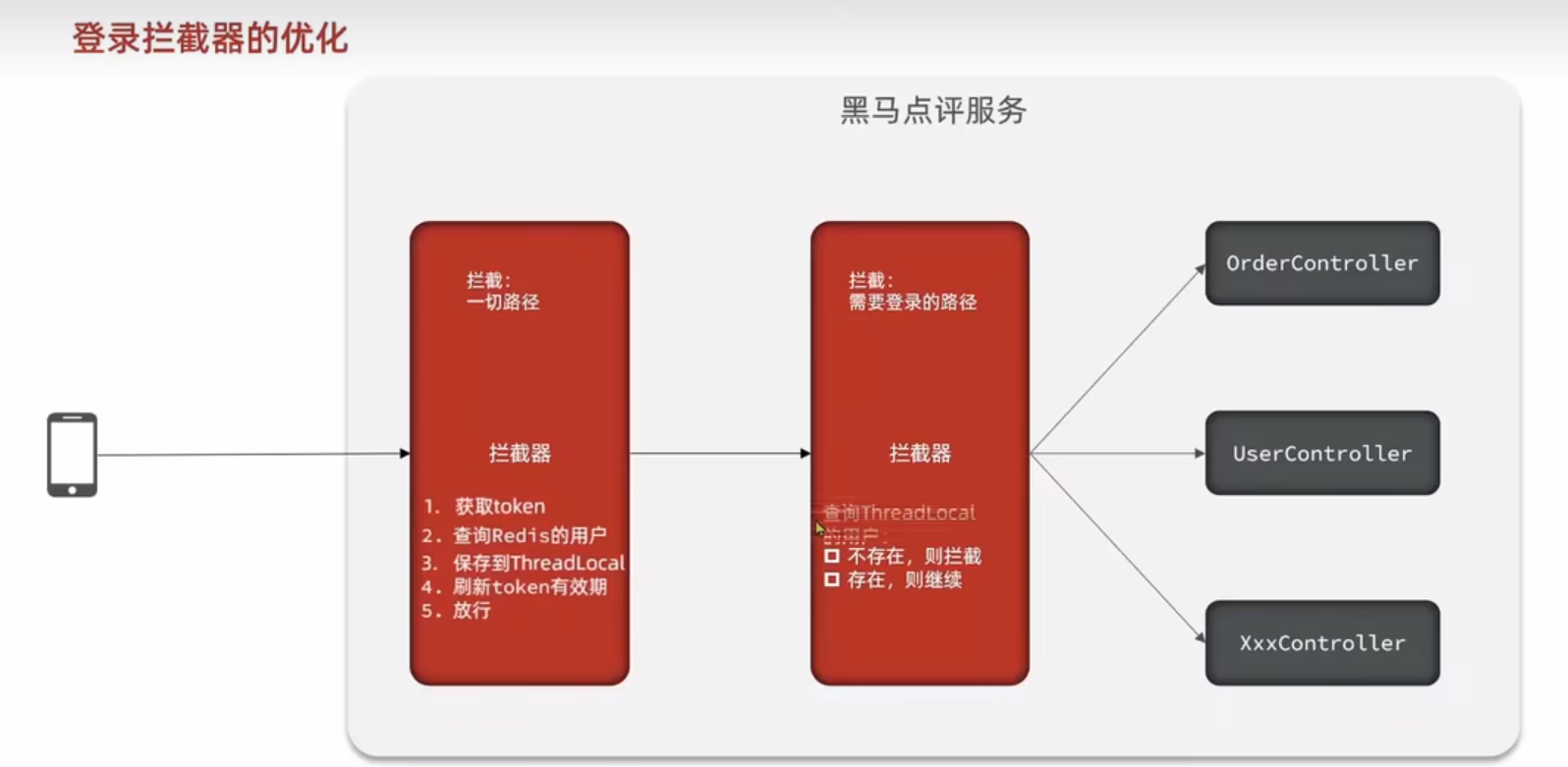
Redis——某马点评day01——短信登录
项目介绍 导入黑马点评项目 项目架构 基于Session实现登录 基本流程 实现发送短信验证码功能 controller层中 /*** 发送手机验证码*/PostMapping("code")public Result sendCode(RequestParam("phone") String phone, HttpSession session) {// 发送短信…...
AES加密技术:原理与应用
一、引言 随着信息技术的飞速发展,数据安全已成为越来越受到重视的领域。加密技术作为保障数据安全的重要手段,在信息安全领域发挥着举足轻重的作用。AES(Advanced Encryption Standard)作为一种对称加密算法,自1990年…...

Unity中PlayerPrefs在PC上存储位置总结
编辑器下和EXE存储位置是不同的,这也不难理解,是为了避免存储位置相同导致开发和测试冲突。 编辑器下位置:HKEY_CURRENT_USER\Software\Unity\UnityEditor\ExampleCompanyName\ExampleProductName EXE位置:HKEY_CURRENT_USER\Sof…...

消融实验:深度学习的关键分析工具
消融实验:深度学习的关键分析工具 在深度学习和机器学习领域,消融实验(Ablation Study)是一种重要的实验方法,用于理解和评估模型的各个组成部分对其整体性能的贡献。通过这种方法,研究人员可以更深入地了…...

Redis缓存——Spring Cache入门学习
Spring Cache 介绍 Spring Cache 是一个框架,实现了基于注解的缓存功能,只需要简单地加一个注解,就能实现缓存功能。 Spring Cache 提供了一层抽象,底层可以切换不同的缓存实现,例如: EHCacheCaffeineR…...

Python标准库copy【侯小啾python领航班系列(十五)】
Python标准库copy【侯小啾python领航班系列(十五)】 大家好,我是博主侯小啾, 🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

「全栈技术解析」推客小程序系统开发:从架构设计到裂变增长的完整解决方案
在移动互联网营销竞争白热化的当下,推客小程序系统凭借其裂变传播、精准营销等特性,成为企业抢占市场的利器。本文将深度解析推客小程序系统开发的核心技术与实现路径,助力开发者打造具有市场竞争力的营销工具。 一、系统核心功能架构&…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...
