MATLAB 模型参考自适应控制 - Model Reference Adaptive Control
系列文章目录
文章目录
- 系列文章目录
- 前言
- 一、参考模型
- 二、扰动与不确定性模型
- 三、直接 MRAC
- 名义模型
- 参数更新
- 间接 MRAC
- 估计器模型和控制器增益
- 参数更新
- 学习修正
- 参考文献
前言
模型参考自适应控制模块计算控制动作,使不确定的受控系统跟踪给定参考被控对象模型的行为。使用该程序块,可以实现以下模型参考自适应控制 (MRAC) 算法。
-
直接 MRAC - 根据被控对象与参考工厂模型状态之间的实时跟踪误差,估算反馈和前馈控制器增益。
-
间接 MRAC - 根据参考设备模型与估计系统状态之间的跟踪误差,估计被控对象系统的参数。然后,根据估计系统和参考模型的参数推导出反馈和前馈控制器增益。
直接和间接 MRAC 还能估算被控系统的外部干扰和不确定性模型。然后,控制器在计算控制动作时使用该模型对干扰和不确定性进行补偿。
在这两种情况下,控制器都会根据跟踪误差实时更新估计参数和干扰模型。
一、参考模型
对于直接和间接 MRAC 而言,以下参考被控对象模型是理想的系统,它描述了您在实践中想要实现的理想行为。
x ˙ m ( t ) = A m x m ( t ) + B m r ( t ) {\dot{x}}_{m}(t)=A_{m}x_{m}(t)+B_{m}r(t) x˙m(t)=Amxm(t)+Bmr(t)
此处
-
r(t) 是外部参考信号。
-
xm(t) 是被控对象模型的状态。由于 r(t) 已知,因此可以通过模拟参考模型得到 xm(t)。
-
Am 是恒定状态矩阵。对于一个稳定的参考模型,Am 必须是一个 Hurwitz 矩阵,其每个特征值都必须是严格的负实部。
-
Bm 是控制有效矩阵。
二、扰动与不确定性模型
模型参考自适应控制模块维护着受控系统中干扰和模型不确定性的内部模型 u a d u_{a d} uad。
u a d = w T ϕ ( x ) u_{a d}=w^{T}\phi(x) uad=wTϕ(x)
w 是控制器根据跟踪误差实时更新的自适应控制权重向量。
要定义 ϕ(x),可以使用以下特征定义之一。
-
被控对象的状态向量 - 这种方法可能无法充分反映系统的不确定性。在不了解干扰和模型不确定性的复杂性时,使用状态作为特征可能是一个有用的起点。
-
高斯径向基函数 - 当扰动和模型的不确定性是非线性的,且扰动模型的结构未知时,请使用此选项。径向基函数要求事先了解模型的运行域,这在某些情况下可能比较困难。
-
单隐层神经网络 - 当扰动和模型的不确定性是非线性的,扰动模型的结构未知,并且您没有运行域的先验知识时,请使用此选项。神经网络是一种通用函数近似器,可以近似任何连续函数。
-
提供给控制器模块的外部源 - 使用该选项可自定义特征向量。如果您知道干扰和不确定性模型的结构,则可以使用该选项。例如,您可以使用自定义特征向量来确定特定的未知被控对象参数。
三、直接 MRAC
直接 MRAC 控制器的控制结构如下
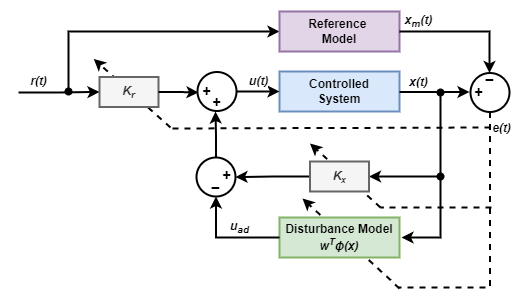
控制器计算控制输入 u(t) 的方法如下
u ( t ) = k x x ( t ) + k r r ( t ) − u a d u a d = w T ϕ ( x ) \begin{array}{c}{{u(t)=k_{x}x(t)+k_{r}r(t)-u_{a d}}}\\ {{u_{a d}=w^{T}\phi(x)}}\end{array} u(t)=kxx(t)+krr(t)−uaduad=wTϕ(x)
此处
-
x(t) 是受控系统的状态。
-
r(t) 是外部参考信号。
-
kx 和 kr 分别是反馈和前馈控制器增益。
-
u a d u_{a d} uad 是根据扰动模型得出的自适应控制分量。
ϕ ( x ) \phi(x) ϕ(x) 包含干扰模型特征。 -
w 是自适应扰动模型权重向量。
-
V 是隐藏层权重向量。
对于单隐层神经网络, u a d u_{a d} uad 为
u a d = w T σ ( V T x ) u_{a d}=w^{T}\sigma(V^{T}x) uad=wTσ(VTx)
此处
-
V 是隐层权重向量。
-
σ 是 sigmoid 激活函数。
控制器计算受控系统状态与参考模型状态之间的误差 e(t)。然后利用该误差实时调整 kx、kr 和 w 的值。
名义模型
受控系统通常具有建模不确定性和外部干扰,其标称状态方程如下。控制器在更新控制器参数时,会使用这一预期的标称被控对象行为。
x ˙ ( t ) = A x ( t ) + B ( u ( t ) + f ( x ) ) {\dot{x}}(t)=A x(t)+B(u(t)+f(x)) x˙(t)=Ax(t)+B(u(t)+f(x))
这里的
-
x(t) 是要控制系统的状态。
-
u(t) 是控制输入。
-
A 是恒定的状态转换矩阵。
-
B 是恒定的控制有效矩阵。
-
f(x) 是系统中匹配的不确定性。
参数更新
直接 MRAC 控制器使用以下公式更新状态矢量、径向基函数和外部源特征定义的控制器增益和干扰模型权重
k ˙ x = Γ x x ( t ) e T ( t ) P B k ˙ r = Γ r r ( t ) e T ( t ) P B w ˙ = Γ w ϕ ( x ) e T ( t ) P B \begin{array}{l}{{\dot{k}_{x}=\Gamma_{x}x(t)e^{T}(t)P B}}\\ {{\dot{k}_{r}=\Gamma_{r}r(t)e^{T}(t)P B}}\\ {{\dot{w}=\Gamma_{w}\phi(x)e^{T}(t)P B}}\end{array} k˙x=Γxx(t)eT(t)PBk˙r=Γrr(t)eT(t)PBw˙=Γwϕ(x)eT(t)PB
单隐层干扰模型更新方程使用相同的控制器增益更新和以下更新方程。
w ˙ = − ( σ ( V T x ) − σ ′ ( V T x ) V T x ) e T ( t ) P B Γ w V ˙ = − Γ V x e T ( t ) P B w T σ ( V T x ) \begin{array}{l}{{\dot{w}=-(\sigma(V^{T}x)-{{\sigma}}^{\prime}(V^{T}x)V^{T}x){{e}}^{T}(t){{P}}{{B}}\Gamma_{w}}}\\ {{\dot{V}=-\Gamma{{V}}{{x}}{{e}}^{T}(t){{P}}{{B}}w^{T}{{\sigma}}(V^{T}x)}}\end{array} w˙=−(σ(VTx)−σ′(VTx)VTx)eT(t)PBΓwV˙=−ΓVxeT(t)PBwTσ(VTx)
Here, P is the solution to the following Lyapunov function based on the reference model state matrix and B is the control effective matrix from the nominal plant model.
A m T P + P A m + Q = 0 A_{m}^{T}P+P A_{m}+Q=0 AmTP+PAm+Q=0
这里,Q 是大小为 N 乘 N 的正定矩阵,其中 N 是状态向量 x(t) 的大小
间接 MRAC
间接 MRAC 控制器的控制结构如下。参考模型为
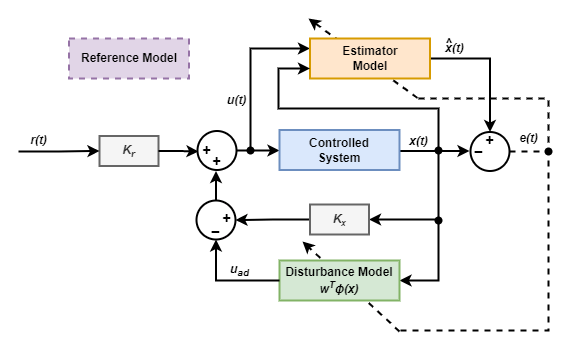
控制器计算控制输入 u(t) 的方法如下
u ( t ) = k x x ( t ) + k r r ( t ) − u a d u a d = w T ϕ ( x ) \begin{array}{c}{{u(t)=k_{x}x(t)+k_{r}r(t)-u_{a d}}}\\ {{u_{a d}=w^{T}\phi(x)}}\end{array} u(t)=kxx(t)+krr(t)−uaduad=wTϕ(x)
这里:
-
x ^ ( t ) \hat{x}(t) x^(t) 是由估计模型产生的受控系统估计状态。
-
r(t) 是外部参考信号。
-
kx 和 kr 分别是反馈和前馈控制器增益。
-
u a d u_{a d} uad 是根据扰动模型得出的自适应控制分量。
-
ϕ ( x ) \phi(x) ϕ(x) 包含干扰模型特征。
-
w 是自适应扰动模型权重向量。
控制器计算实际系统状态和估计系统状态之间的误差 e(t)。然后利用该误差实时调整 w 的值。控制器还利用 e(t) 实时更新估计模型的参数。增益 kx 和 kr 的值来自估计模型和参考模型的参数。
估计器模型和控制器增益
间接 MRAC 控制器包含以下受控系统的估计模型。
x ^ ˙ ( t ) = A ^ x ( t ) + B ^ u ( t ) \dot{\hat{x}}(t)=\hat{A}x(t)+\hat{B}u(t) x^˙(t)=A^x(t)+B^u(t)
这里:
-
x ^ ˙ ( t ) \dot{\hat{x}}(t) x^˙(t) 是估计的系统状态。
-
u ( t ) u(t) u(t) 是控制输入。
-
A ^ \hat{A} A^ 是估计器的状态转换矩阵。
-
B ^ \hat{B} B^ 是估计器的控制有效矩阵。
在运行过程中,控制器基于估计误差 e(t)更新 A ^ \hat{A} A^ 和 B ^ \hat{B} B^ 。
间接 MRAC 控制器不直接估算控制器增益,而是采用基于动态反演的方法,从参考模型和估算模型的参数中推导出反馈增益 k x k_x kx 和前馈增益 k r k_r kr,具体如下。
k r = B m B ^ k x = 1 B ^ ( A m − A ^ ) \begin{array}{c}{{k_r={\displaystyle\dfrac{B_m}{\hat{B}}}}}\\ {{k_{x}={\displaystyle\frac{1}{\hat{B}}}\left(A_m-\hat{A}\right)}}\end{array} kr=B^Bmkx=B^1(Am−A^)
这里, 1 B ^ \displaystyle\frac{1}{\hat{B}} B^1 是矩阵 B ^ \hat{B} B^ 的 Moore-Penrose 摩尔-彭罗斯伪逆。
参数更新
间接 MRAC 控制器使用以下公式更新状态矢量、径向基函数和外部源特征定义的估计模型参数和干扰模型权重
A ^ ˙ = Γ a x ( t ) e T ( t ) P B ^ ˙ = Γ b u ( t ) e T ( t ) P w ˙ = Γ w ϕ ( x ) e T ( t ) P B \begin{array}{l}{{\dot{\hat{A}}=\Gamma_{a}x(t)e^{T}(t)P}}\\ {{\dot{\hat{B}}=\Gamma_{b u(t)}e^T{(t)P}}}\\ {{\dot{w}=\Gamma_{w}\phi(x)e^T{(t)P B}}}\end{array} A^˙=Γax(t)eT(t)PB^˙=Γbu(t)eT(t)Pw˙=Γwϕ(x)eT(t)PB
单隐层干扰模型更新方程使用相同的估计模型参数更新和以下更新方程。
w ˙ = − ( σ ( V T x ) − σ ′ ( V T x ) V T x ) e T ( t ) P B Γ w V ˙ = − Γ V x e T ( t ) P B w T σ ( V T x ) \begin{array}{l}{{\dot{w}=-(\sigma(V^{T}x)-{{\sigma}}^{\prime}(V^{T}x)V^{T}x){{e}}^{T}(t){{P}}{{B}}\Gamma_{w}}}\\ {{\dot{V}=-\Gamma{{V}}{{x}}{{e}}^{T}(t){{P}}{{B}}w^{T}{{\sigma}}(V^{T}x)}}\end{array} w˙=−(σ(VTx)−σ′(VTx)VTx)eT(t)PBΓwV˙=−ΓVxeT(t)PBwTσ(VTx)
这里,P 是以下 Lyapunov 函数的解。
k τ T P + P k τ + Q = 0 k_{\tau}^{T}P+P k_{\tau}+Q=0 kτTP+Pkτ+Q=0
kτ 是估计器反馈增益。默认情况下,该值与参考模型状态转换矩阵 Am 相对应。不过,也可以指定不同的估计器反馈增益值。
学习修正
对于直接和间接 MRAC,为了在更高的学习率下增加稳健性,可以修改参数更新,加入一个可选的动量项。您可以从两种可能的学习修改方法中选择一种:sigma 和 e-modification。
对于西格玛修正,每次参数更新的动量项都是动量权重参数 σ 与当前参数值的乘积。例如,以下直接 MRAC 控制器的更新方程就包含了 σ 修正项。
k ˙ x = Γ x x ( t ) e T ( t ) P B + σ k x k ˙ r = Γ r r ( t ) e T ( t ) P B + σ k x w ˙ x = Γ w ϕ ( t ) e T ( t ) P B + σ w \begin{array}{l}{{\dot{k}_{x}=\Gamma_{x}x(t)e^{T}(t)P B+\sigma k_{x}}}\\ {{\dot{k}_{r}=\Gamma_{r}r(t)e^{T}(t)P B+\sigma k_{x}}}\\ {{\dot{w}_{x}=\Gamma_{w}\phi(t)e^{T}(t)P B+\sigma w}}\end{array} k˙x=Γxx(t)eT(t)PB+σkxk˙r=Γrr(t)eT(t)PB+σkxw˙x=Γwϕ(t)eT(t)PB+σw
对于 e-修正,控制器通过误差矢量的规范对 sigma-修正动量项进行缩放。例如,以下间接 MRAC 控制器的更新方程就包含了一个 e 修正项。
A ^ ˙ = Γ a x ( t ) e T ( t ) P + σ ∣ e ( t ) ∣ A ^ B ^ ˙ = Γ b u ( t ) e T ( t ) P + σ ∣ e ( t ) ∣ B ^ w ˙ x = Γ w ϕ ( t ) e T ( t ) P B + σ ∣ e ( t ) ∣ w \begin{array}{l}{{\dot{\hat{A}}=\Gamma_{a}x(t)e^{T}(t)P+\sigma|e(t)|\hat{A}}}\\ {{\dot{\hat{B}}=\Gamma_{b}u(t)e^{T}(t)P+\sigma|e(t)|\hat{B}}}\\ {{\dot{w}_{x}=\Gamma_{w}\phi(t)e^{T}(t)P B+\sigma|e(t)|w}}\end{array} A^˙=Γax(t)eT(t)P+σ∣e(t)∣A^B^˙=Γbu(t)eT(t)P+σ∣e(t)∣B^w˙x=Γwϕ(t)eT(t)PB+σ∣e(t)∣w
要调整这两种方法的学习修正量,可改变动量权重参数 σ 的值。
参考文献
[1] Ioannou, Petros A., and Jing Sun. Robust adaptive control, Courier Corporation, 2012.
[2] Narendra, Kumpati S, and Anuradha M Annaswamy. Stable Adaptive Systems. Courier Corporation, 2012.
[3] Narendra, Kumpati S., and Anuradha M. Annaswamy. “Robust Adaptive Control.” In 1984 American Control Conference, 333–35. San Diego, CA, USA: IEEE, 1984. https://doi.org/10.23919/ACC.1984.4788398
相关文章:

MATLAB 模型参考自适应控制 - Model Reference Adaptive Control
系列文章目录 文章目录 系列文章目录前言一、参考模型二、扰动与不确定性模型三、直接 MRAC名义模型参数更新间接 MRAC估计器模型和控制器增益参数更新学习修正参考文献 前言 模型参考自适应控制模块计算控制动作,使不确定的受控系统跟踪给定参考被控对象模型的行为…...

【如何用批处理文件实现自动编译Keil工程和C# Visual Studio工程】
如何用批处理文件实现自动编译Keil工程和C# Visual Studio工程 写个Bat 批处理文件,现自动编译Keil工程和C# Visual Studio工程。这样可以结合Python 实现复杂的操作。 编译Keil工程: echo off set UVC:\Keil_v5\UV4\UV4.exe set UV_PRO_PATHD:\worksp…...

大模型的实践应用11-“书生”通用大模型的搭建与模型代码详细介绍,以及快速使用方法
大家好,我是微学AI,今天给大家介绍一下大模型的实践应用11-“书生”通用大模型的搭建与模型代码详细介绍,以及快速使用方法。“书生” 通用大模型是上海人工智能实验室研制的大模型,并且已经开源了“书生浦语”大模型70亿参数的轻量级版本InternLM-7B。InternLM-7B模型主要…...

【开发PaaS】基于Postgresql的开发平台Supabase
Supadase是开源的。我们选择可扩展的开源工具,使其易于使用。 Supadase不是Firebase的1对1映射。虽然我们正在构建Firebase提供的许多功能,但我们不会以同样的方式进行: 我们的技术选择大不相同;我们使用的一切都是开源的&#…...

前端开启gzip优化页面加载速度
生成gizp的打包资源,可以优化页面加载速度 打包的时候开启gzip可以很大程度减少包的大小,页面大小可以变为原来的30%甚至更小,非常适合线上部署, 但还记得需要服务端支持 1、前端配置compression-webpack-plugin 先安装:npm install compres…...

用Java写一个俄罗斯方块
目录 游戏规则 小方块类:Cell 七种图形类:I、J、L、O、S、T、Z J L O S T Z 俄罗斯方块游戏主类:Tetris 效果展示 游戏规则 由小方块组成的不同形状的板块陆续从屏幕上方落下来,玩家通过调整板块的位置和方向,使它…...

应用于智慧金融的AI边缘计算盒子+AI算法软硬一体化方案
传统金融营业厅存在运营管理模式落后、资源投放不平衡、从业人员培训效果不达预期、客户体验割裂等普遍现象; 部署英码数字金融解决方案,将助力企业从传统金融模式快速向数字金融模式转变,可针对每一个客户定制个性化“一对一”服务ÿ…...

目标检测——Faster R-CNN算法解读
论文:Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks 作者:Shaoqing Ren, Kaiming He, Ross Girshick, and Jian Sun 链接:https://arxiv.org/abs/1506.01497 代码:https://github.com/rbgirsh…...
安装入门 —— 软件介绍)
Wireshark (一)安装入门 —— 软件介绍
文章目录 Wireshark是什么?为什么要使用Wireshark?相关网络分析工具软件对比 Wireshark是什么? Wireshark是一种开源网络协议分析器,它可以捕获和分析网络中传输的数据包。 用户可以使用Wireshark来诊断网络问题、了解网络协议的…...
Web框架与Django路由层
Web框架 一 web框架 Web框架(Web framework)是一种开发框架,用来支持动态网站、网络应用和网络服务的开发。这大多数的web框架提供了一套开发和部署网站的方式,也为web行为提供了一套通用的方法。web框架已经实现了很多功能&…...

什么是CAS, 什么是AQS
文章目录 什么是CAS, 什么是AQSCASAQS 什么是CAS, 什么是AQS CAS AQS AQS 全称是AbstractQueuedSynchronizer, 是juc 下一个核心的抽象类,用于构建各种同步器和锁 比如我们熟悉的 ReentrantLock、ReadWriteLock、CountDownLatch等等是基于AQS. 首先在…...
蓝桥杯每日一题2023.12.1
题目描述 蓝桥杯大赛历届真题 - C 语言 B 组 - 蓝桥云课 (lanqiao.cn) 题目分析 对于此题目而言思路较为重要,实际可以转化为求两个数字对应的操作,输出最前面的数字即可 #include<bits/stdc.h> using namespace std; int main() {for(int i 1…...

正则表达式从放弃到入门(1):“正则表达式”是什么?
正则表达式从放弃到入门(1):“正则表达式”是什么? 本博文转载自 这是一篇”正则表达式”扫盲贴,如果你还不理解什么是正则表达式,看这篇文章就对了。 如果你已经掌握了”正则表达式”,就不用再…...

SQL解惑 - 谜题2
文章目录 一、谜题描述二、分析三、答案四、总结 一、谜题描述 创建一个记录雇员缺勤率的数据库。使用的表结构如下:Absenteeism 主键:PRIMARY KEY (emp_id, absent_date) 字段名字段类型字段中文名字段描述emp_idINTERGER雇员id-absent_dateSTRING缺勤…...

FWT+高维前缀和:Gym - 103202M
https://vj.imken.moe/contest/597216#problem/F 考虑两个人的集合分别为 i , j i,j i,j,那么我们令 f ( i ⊗ j ) f(i\otimes j) f(i⊗j),其中 f ( s ) f(s) f(s) 表示两个人不同集合恰好为 s s s,显然 f ( s ) f(s) f(s) 可以FWT求…...

【C++】string类的接口综合运用
目录 介绍: 一,string对象的构建 二,string类对象的容量操作 介绍: string容器我们之前已经粗略了解了基本增添、修改、删除、插入等基本功能,这里就不再做过多说明,接下来我们全面并详细…...

分布式ID生成框架Leaf升级踩坑
背景: 在项目中需要一个统一的拿单号等唯一ID的服务,就想起了之前用到的leaf,但是因为项目要求,leaf的版本不符合,需要做一些升级 项目地址:https://github.com/Meituan-Dianping/Leaf 升级点࿱…...
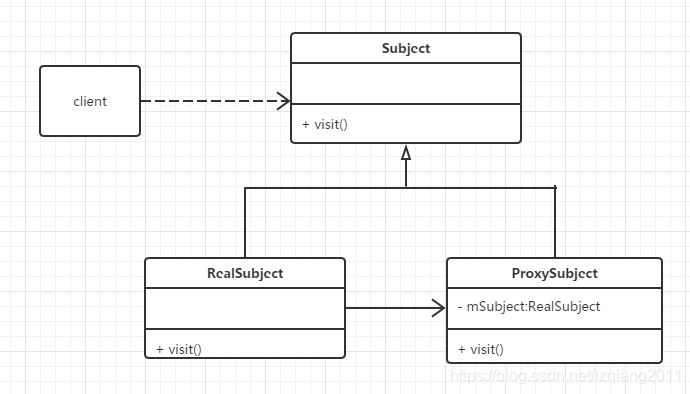
常用的设计模式
文章目录 常用的设计模式:一、单例模式3、懒汉式 - 懒汉式非线程安全4、饿汉式 - 线程安全5、懒汉式和饿汉式区别6、双重检查锁定7、应用场景 二、工厂模式1、简单工厂模式2、工厂模式3、抽象工厂4、总结 三、代理模式1、静态代理2、动态代理jdk自带动态代理 3、Cgl…...
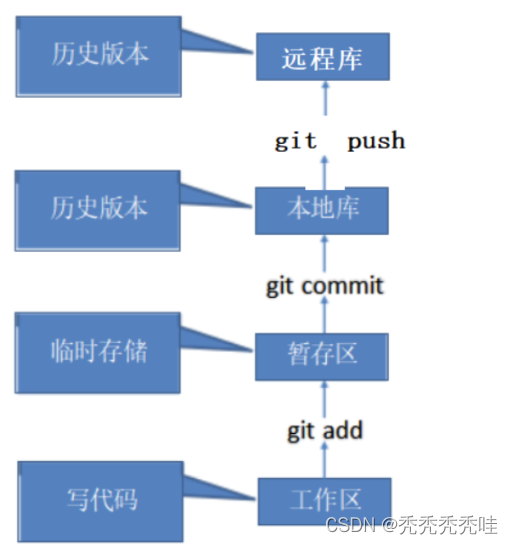
git的相关实用命令
参看文章:https://blog.csdn.net/qq_21688871/article/details/130158888 http://www.mobiletrain.org/about/BBS/159885.html 1、git commit后,但发现文件有误,不想push(提交到本地库,回退到暂存区) git reset --sof…...

【使用`model.status`来获取gurobi求解过程中的模型状态】
在Gurobi中,你可以使用model.status来获取求解过程中的模型状态。可以使用了model.status来检查模型是否找到最优解。模型状态是一个Gurobi的常量,表示了求解过程中的不同状态。 以下是一些常见的模型状态: GRB.OPTIMAL: 最优解被找到。GRB…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...
