代数学笔记9: 群的直积,可解群,自由群,群表示
群的直积
外直积
H 1 , H 2 H_1,H_2 H1,H2是两个群(固定的群), 且有 G = H 1 × H 2 G=H_1\times H_2 G=H1×H2,(构造的新群)
G = ( { ( h 1 , h 2 ) ∣ h 1 ∈ H 1 , h 2 ∈ H 2 } , ⋅ ) , G=\big(\{(h_1,h_2)|h_1\in H_1,h_2\in H_2\},\cdot\big), G=({(h1,h2)∣h1∈H1,h2∈H2},⋅),
定义运算:
( h 1 , h 2 ) ⋅ ( g 1 , g 2 ) ≜ ( h 1 g 1 , h 2 g 2 ) , ∀ h 1 , g 1 ∈ H 1 , h 2 , g 2 ∈ H 2 . (h_1,h_2)\cdot(g_1,g_2)\triangleq(h_1g_1,h_2g_2),\quad \forall h_1,g_1\in H_1,h_2,g_2\in H_2. (h1,h2)⋅(g1,g2)≜(h1g1,h2g2),∀h1,g1∈H1,h2,g2∈H2.
并且有:
H 1 × { e 2 } = { ( h 1 , e 2 ) ∣ ∀ h 1 ∈ H 1 , e 2 ∈ H 2 } ≅ H 1 ⊴ G . H_1\times\{e_2\}=\{(h_1,e_2)|\forall h_1\in H_1,e_2\in H_2\}\cong H_1\unlhd G. H1×{e2}={(h1,e2)∣∀h1∈H1,e2∈H2}≅H1⊴G.
内直积
与外直积相反, G G G是一个群, 如果 H 1 , H 2 ⊴ G H_1,H_2\unlhd G H1,H2⊴G且 H 1 ∩ H 2 = { e } H_1\cap H_2=\{e\} H1∩H2={e}, G = H 1 H 2 G=H_1H_2 G=H1H2, 则称 G ≅ H 1 × H 2 G\cong H_1\times H_2 G≅H1×H2.
证明:
∀ g ∈ G , g = h 1 h 2 \forall g\in G,g=h_1h_2 ∀g∈G,g=h1h2, 其中 h 1 ∈ H 1 , h 2 ∈ H 2 h_1\in H_1,h_2\in H_2 h1∈H1,h2∈H2;
H 1 ∩ H 2 = { e } H_1\cap H_2=\{e\} H1∩H2={e} 上面的表示方法唯一.
若不然, g = h 1 h 2 = g 1 g 2 g=h_1h_2=g_1g_2 g=h1h2=g1g2, 两边左乘 g 1 − 1 g_1^{-1} g1−1,右乘 h 2 − 1 h_2^{-1} h2−1, 得到
H 1 ∋ g 1 − 1 h 1 = g 2 h 2 − 1 ∈ H 2 , ⟺ g 1 − 1 h 1 = g 2 h 2 − 1 = e . H_1\ni g_1^{-1}h_1=g_2h_2^{-1}\in H_2,\iff g_1^{-1}h_1=g_2h_2^{-1}=e. H1∋g1−1h1=g2h2−1∈H2,⟺g1−1h1=g2h2−1=e.于是 H 1 × H 2 ⟶ G : ( h 1 , h 2 ) ⟼ h 1 h 2 H_1\times H_2\longrightarrow G:(h_1,h_2)\longmapsto h_1h_2 H1×H2⟶G:(h1,h2)⟼h1h2.
直积的意义:
G = H 1 × H 2 , G > H 1 > { i d } , ⟺ G / H 1 ≅ H 2 . G= H_1\times H_2, G>H_1>\{{\rm id}\},\iff G/H_1\cong H_2. G=H1×H2,G>H1>{id},⟺G/H1≅H2.
例子:
S 3 × S 3 \mathcal{S}_3\times \mathcal{S}_3 S3×S3,(36阶群) 则
S 3 ≅ ( { ( a , a ) ∣ a ∈ S 3 } , ⋅ ) ≅ S 3 × { ( 1 ) } = { ( 1 ) } × S 3 \mathcal{S}_3\cong\big(\{(a,a)|a\in\mathcal{S}_3\},\cdot\big)\\ \qquad\quad\cong\mathcal{S}_3\times \{(1)\}=\{(1)\}\times \mathcal{S}_3 S3≅({(a,a)∣a∈S3},⋅)≅S3×{(1)}={(1)}×S3
第一行不是 S 3 × S 3 \mathcal{S}_3\times \mathcal{S}_3 S3×S3的正规子群, 但是第二行是.
例子:(交换群, 等价于 d i d_i di阶循环群的直积)
G = C d 1 × ⋯ × C d n , C d ≅ ( Z / d Z , + ) = ⟨ g ⟩ , g d = e . G=C_{d_1}\times\cdots \times C_{d_n},\quad C_{d}\cong(\mathbb{Z}/d\mathbb{Z},+)=\langle g\rangle,\quad g^d=e. G=Cd1×⋯×Cdn,Cd≅(Z/dZ,+)=⟨g⟩,gd=e.
对于具体的例子: C 4 × C 8 C_4\times C_8 C4×C8,
有几个4阶群, 有几个8阶群?
Sol.
通过循环群的定义计算,
半直积
H 1 ⊴ G , G / H 1 ≅ H 2 H_1\unlhd G,G/H_1\cong H_2 H1⊴G,G/H1≅H2, 则 G = H 1 ⋉ H 2 G=H_1\ltimes H_2 G=H1⋉H2.
- 如果 H 1 , H 2 H_1,H_2 H1,H2为循环群, G G G称为亚循环群.
可解群
正规子群链:
G = G 0 ⊃ G 1 ⊃ ⋯ G i ⊃ G i + 1 ⊃ ⋯ ⊃ G n = { e } , G=G_0\supset G_1\supset \cdots G_i\supset G_{i+1}\supset \cdots\supset G_n=\{e\}, G=G0⊃G1⊃⋯Gi⊃Gi+1⊃⋯⊃Gn={e},
其中 G i ⊴ G i − 1 G_i\unlhd G_{i-1} Gi⊴Gi−1.
合成群链(中间的任意两个商群都是单群, 或者中间找不到子群, 使正规子群链成立)
-
循环群的合成群链:
由循环群结构定理:
G ≅ C n ≅ ( Z / n Z , + ) , ∀ m ∣ n , ( m Z / n Z , + ) , G\cong C_n\cong (\mathbb{Z}/n\mathbb{Z},+), \forall m|n, (m\mathbb{Z}/n\mathbb{Z},+), G≅Cn≅(Z/nZ,+),∀m∣n,(mZ/nZ,+),
得到: 若 n = p 1 ⋯ p s n=p_1\cdots p_s n=p1⋯ps, 则有
G = Z / n Z > p 1 Z / n Z > p 1 p 2 Z / n Z > ⋯ > p 1 ⋯ p s Z / n Z = { e } . G=\mathbb{Z}/n\mathbb{Z}>p_1\mathbb{Z}/n\mathbb{Z}>p_1p_2\mathbb{Z}/n\mathbb{Z}>\cdots>p_1\cdots p_s\mathbb{Z}/n\mathbb{Z}=\{e\}. G=Z/nZ>p1Z/nZ>p1p2Z/nZ>⋯>p1⋯psZ/nZ={e}. -
交换群的合成群链:
由交换群结构定理,
G ≅ Z / d 1 Z × Z / d 2 Z × ⋯ × Z / d n Z , d 1 ∣ d 2 , ⋯ , d n − 1 ∣ d n , G\cong \mathbb{Z}/d_1\mathbb{Z}\times \mathbb{Z}/d_2\mathbb{Z}\times\cdots\times \mathbb{Z}/d_n\mathbb{Z}, \quad d_1|d_2,\cdots,d_{n-1}|d_n, G≅Z/d1Z×Z/d2Z×⋯×Z/dnZ,d1∣d2,⋯,dn−1∣dn,
于是我们有
G > Z / d 1 Z × ⋯ × Z / d n − 1 Z × { 1 } > ⋯ > Z / d 1 Z × { 1 } × ⋯ × { 1 } ⏟ n − 1 个 > { 1 } G>\mathbb{Z}/d_1\mathbb{Z}\times\cdots\times \mathbb{Z}/d_{n-1}\mathbb{Z}\times\{1\}>\cdots>\mathbb{Z}/d_1\mathbb{Z}\times\underbrace{\{1\}\times\cdots\times\{1\}}_{n-1个}>\{1\} G>Z/d1Z×⋯×Z/dn−1Z×{1}>⋯>Z/d1Z×n−1个 {1}×⋯×{1}>{1} -
p-群的合成群链:
G G G不交换, 则 Z ( G ) ≠ { 1 } \mathbb{Z}(G)\ne\{1\} Z(G)={1},
G > Z ( G ) > { 1 } . G>\mathbb{Z}(G)>\{1\}. G>Z(G)>{1}.
即 ∣ G ∣ = p n |G|=p^n ∣G∣=pn,
G > G 1 > ⋯ > G n = { 1 } G>G_1>\cdots>G_n=\{1\} G>G1>⋯>Gn={1}
其中 ∣ G i ∣ = p n − i |G_i|=p^{n-i} ∣Gi∣=pn−i,G G G交换, 直接由上述讨论得到.
G G G可解 ⟺ G i / G i + 1 \iff G_{i}/G_{i+1} ⟺Gi/Gi+1为素数阶循环群.
应用Sylow定理:
p a q p^aq paq阶群必可解( p , q p,q p,q为素数, a ∈ Z a\in \mathbb{Z} a∈Z).
证明:
具体的例子: 56 = 2 3 ⋅ 7 56=2^3\cdot7 56=23⋅7, 只有如下几种可能.(由Sylow第三定理)
n 2 = 1 , 7 n 7 = 1 , 8 n_2=1,7\\ n_7=1,8 n2=1,7n7=1,8
如果 n 7 = 8 n_7=8 n7=8, 则有8个7阶子群, 设为 ⟨ g 1 ⟩ , ⋯ , ⟨ g 8 ⟩ \langle g_1\rangle,\cdots,\langle g_8\rangle ⟨g1⟩,⋯,⟨g8⟩, 每个7阶子群有6个7阶元(以及1个单位元)
于是 56 − 6 × 8 = 8 56-6\times8=8 56−6×8=8还剩下8个元素(减掉48个7阶元), 这8个元素构成了Sylow-2群(除单位元之外, 剩下元素都是8阶元),
- ( 8 , 7 ) = 1 (8,7)=1 (8,7)=1, 于是sylow-2群没有7阶元(由Lagrange定理), 这8个非7阶元构成唯一的Sylow-2群, 于是 n 2 = 1 n_2=1 n2=1, 设此sylow-2群为 H H H, 则
G ⊵ H > { e } , ∣ H ∣ = 8. G\unrhd H>\{e\}, |H|=8. G⊵H>{e},∣H∣=8.
于是56阶群可解.
自由群
商群表示
相关文章:

代数学笔记9: 群的直积,可解群,自由群,群表示
群的直积 外直积 H 1 , H 2 H_1,H_2 H1,H2是两个群(固定的群), 且有 G H 1 H 2 GH_1\times H_2 GH1H2,(构造的新群) G ( { ( h 1 , h 2 ) ∣ h 1 ∈ H 1 , h 2 ∈ H 2 } , ⋅ ) , G\big(\{(h_1,h_2)|h_1\in H_1,h_2\in H_2\},\cdot\big), G({(h1,h2)∣h1∈H…...
kali学习
目录 黑客法则: 一:页面使用基础 二:msf和Windows永恒之蓝漏洞 kali最强渗透工具——metasploit 介绍 使用永恒之蓝进行攻击 编辑 使用kali渗透工具生成远程控制木马 渗透测试——信息收集 域名信息收集 黑客法则: 一&…...

《论文阅读》DualGATs:用于对话中情绪识别的双图注意力网络
《论文阅读》DualGATs:用于会话中情感识别的双图注意力网络 前言摘要模型架构DisGAT图构建图关系类型图节点更新SpkGAT图构建图关系类型图节点更新交互模块情绪预测损失函数问题前言 今天为大家带来的是《DualGATs: Dual Graph Attention Networks...
【算法】单调栈题单——字典序最小⭐(一种类型的模板题)
文章目录 题目列表316. 去除重复字母⭐⭐⭐⭐⭐(类型题模板:单调栈,字典序最小)221021天池-03. 整理书架(保留数量为 limit 的字典序最小)402. 移掉 K 位数字(最多删除 k 次 前导零的处理&…...
DockerCompose修改某个服务的配置(添加或编辑端口号映射)后如何重启单个服务使其生效
场景 docker-compose入门以及部署SpringBootVueRedisMysql(前后端分离项目)以若依前后端分离版为例: docker-compose入门以及部署SpringBootVueRedisMysql(前后端分离项目)以若依前后端分离版为例_docker-compose部署java mysql redis-CSDN博客 上面讲了docker c…...

DOM 事件的传播机制
前端面试大全DOM 事件的传播机制 🌟经典真题 🌟事件与事件流 事件流 事件冒泡流 事件捕获流 标准 DOM 事件流 🌟事件委托 🌟真题解答 🌟总结 🌟经典真题 谈一谈事件委托以及冒泡原理 dz…...

(数据结构)顺序表的查找
静态分配代码: #include<stdio.h> #include<stdlib.h> #define MAX 100 typedef struct LinkList {int data[MAX];int lenth; }Link; //初始化 void CreateList(Link* L) {L->lenth 0;for (int i 0; i < MAX; i){L->data[i] 0;} } //插入 …...

vue 解决响应大数据表格渲染崩溃问题
如果可以实现记得点赞分享,谢谢老铁~ 1.场景描述 发起请求获取上万条数据,进行表格渲染,使浏览器卡顿,导致网页崩溃。 2.分析原因 1.大量数据加载,过多操作Dom,消耗性能。 2.表格中包含其他…...
Hdoop学习笔记(HDP)-Part.13 安装Ranger
目录 Part.01 关于HDP Part.02 核心组件原理 Part.03 资源规划 Part.04 基础环境配置 Part.05 Yum源配置 Part.06 安装OracleJDK Part.07 安装MySQL Part.08 部署Ambari集群 Part.09 安装OpenLDAP Part.10 创建集群 Part.11 安装Kerberos Part.12 安装HDFS Part.13 安装Ranger …...

Spring AOP记录接口访问日志
Spring AOP记录接口访问日志 介绍应用范围组成通知(Advice)连接点(JoinPoint)切点(Pointcut)切面(Aspect)引入(Introduction)织入(Weaving&#x…...

分享89个节日PPT,总有一款适合您
分享89个节日PPT,总有一款适合您 89个节日PPT下载链接:https://pan.baidu.com/s/1j6Yj-7UCcUyV4V_S_eGjpQ?pwd6666 提取码:6666 Python采集代码下载链接:采集代码.zip - 蓝奏云 学习知识费力气,收集整理更不易…...

PostgreSQL日志中的SQL记录时机 —— log_statement 和 log_min_duration_statement
最近跟朋友讨论到PostgreSQL日志中的SQL记录时机,研究了下log_statement 和 log_min_duration_statement两个参数,记录一下。 一、 参数简介 1. log_statement ① 作用 控制记录SQL的类型,可选值为: none:关闭&…...
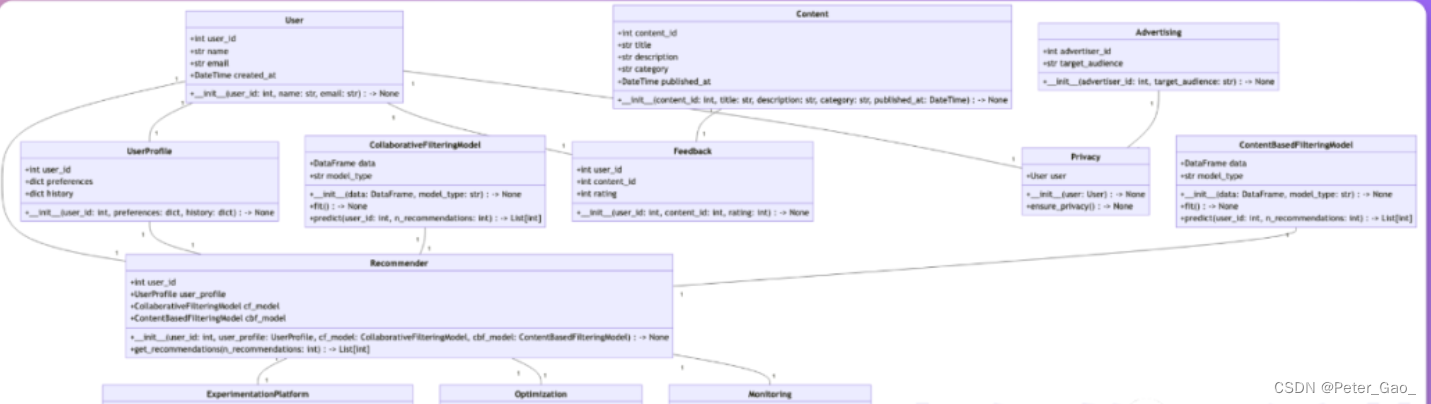
Agent举例与应用
什么是Agent OpenAI 应用研究主管 Lilian Weng 在一篇长文中提出了 Agent LLM(大型语言模型)记忆规划技能工具使用这一概念,并详细解释了Agent的每个模块的功能。她对Agent未来的应用前景充满信心,但也表明到挑战无处不在。 现…...
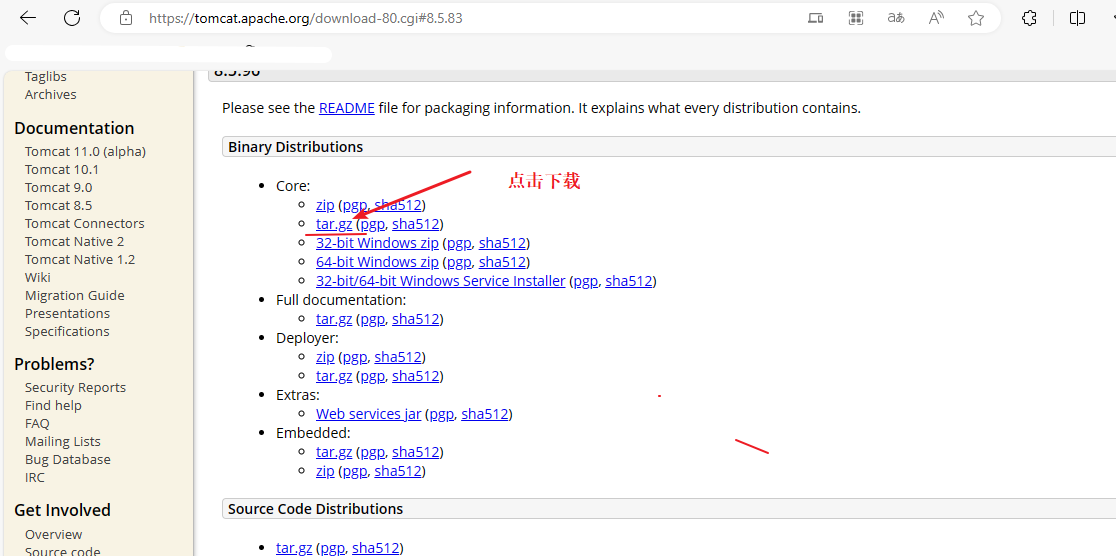
CentOS 7 配置tomcat
简介 Tomcat是一个使用Java编写的开源Web应用服务器,是由Apache Software Foundation管理的一个项目。它是一个轻量级的应用服务器,可以下载、安装和使用,而且还提供了许多高级功能,例如支持Java Servlet、JavaServer Pages (JSP)和JavaServer Faces (JSF) 等JavaEE技术,…...

如何优雅的关闭一个IIS站点
众所周知,当我们使用IIS的时候,在使用负载均衡的情况下,想停掉一个站点,通常会点击Sites(网站)中的Stop(停止)来停止一个站点。但是这样做,会带来一个问题,当…...

弱网模拟工具
一、背景 一个人晚上在家通过 Wi-Fi 上网,在线电影播放基本流畅,可一旦在晚间用网高峰期打视频电话就画面糊,这时不仅可能带宽受限了,还可能有较高的丢包率。与有线网络通信相比,无线网络通信受环境影响会更大&#x…...
)
Leetcode 第 110 场双周赛 Problem D 2809. 使数组和小于等于 x 的最少时间(DP+贪心+正难则反)
Leetcode 第 110 场双周赛 Problem D 2809. 使数组和小于等于 x 的最少时间(DP 好题)题目 给你两个长度相等下标从 0 开始的整数数组 nums1 和 nums2 。每一秒,对于所有下标 0 < i < nums1.length ,nums1[i] 的值都增加 num…...
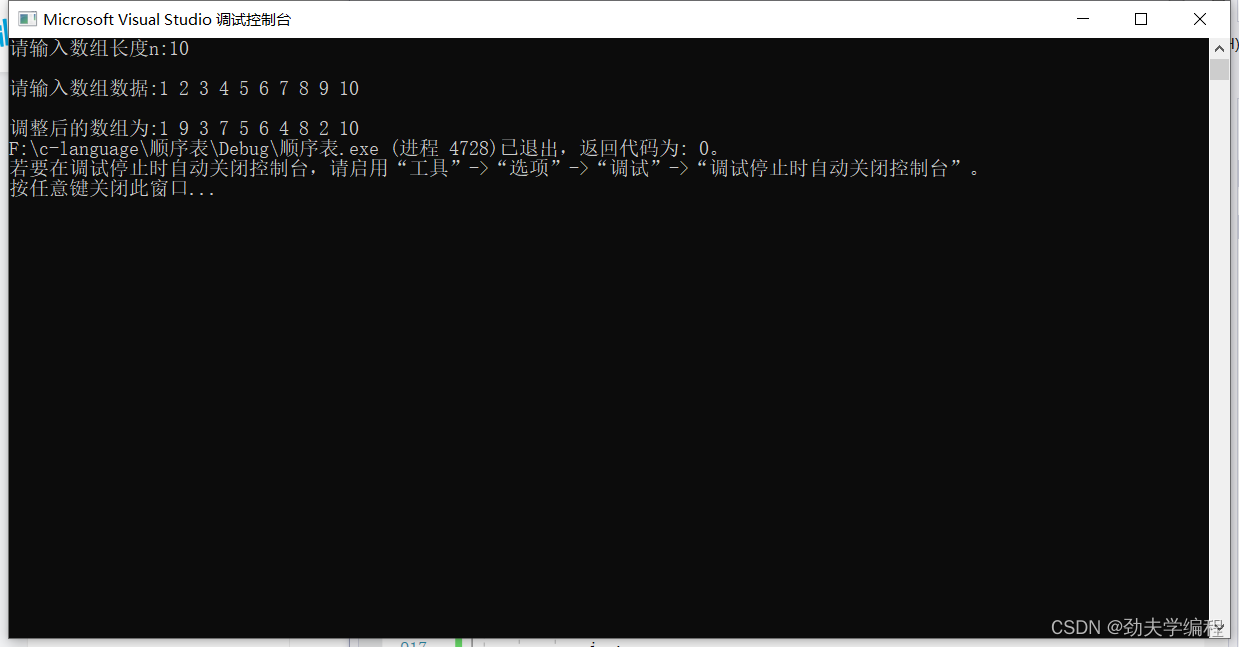
已知数组A[1..n]中元素类型为非负整数,设计算法将其调整为左右两部分,左边所有为奇数,右边所有为偶数,并要求算法的时间复杂度为O(n)
//左边奇数右边偶数 void Swap(int* a, int* b) {int tmp *b;*b *a;*a tmp; } void LeftRight(int arr[],int n) {int i 0;int j n - 1;while(i<j){if (arr[i] % 2 0 && arr[j] % 2 1) {Swap(&arr[i], &arr[j]);i;j--;}else if (arr[i] % 2 1 &…...
ssm+vue的罪犯信息管理系统(有报告)。Javaee项目,ssm vue前后端分离项目。
演示视频: ssmvue的罪犯信息管理系统(有报告)。Javaee项目,ssm vue前后端分离项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构&…...

Java/Android 各类型数据构造和各类型数据解析
Java/Android 各类型数据构造和各类型数据解析 1.如何构造/解析{"key":"value","key":"value","key":"value"}jsonString1)json解析2)fastjson解析3)Gson解析4)遍历key值解析2.如何构造/解析[{"key&q…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...
