Leetcode 第 110 场双周赛 Problem D 2809. 使数组和小于等于 x 的最少时间(DP+贪心+正难则反)
- Leetcode 第 110 场双周赛 Problem D 2809. 使数组和小于等于 x 的最少时间(DP 好题)
- 题目
- 给你两个长度相等下标从 0 开始的整数数组 nums1 和 nums2 。每一秒,对于所有下标 0 <= i < nums1.length ,nums1[i] 的值都增加 nums2[i] 。操作 完成后 ,你可以进行如下操作:
- 选择任一满足 0 <= i < nums1.length 的下标 i ,并使 nums1[i] = 0 。
- 同时给你一个整数 x 。
- 请你返回使 nums1 中所有元素之和 小于等于 x 所需要的 最少 时间,如果无法实现,那么返回 -1 。
- 1 <= nums1.length <= 10 ^ 3
- 1 <= nums1[i] <= 10 ^ 3
- 0 <= nums2[i] <= 10 ^ 3
- nums1.length == nums2.length
- 0 <= x <= 10 ^ 6
- 给你两个长度相等下标从 0 开始的整数数组 nums1 和 nums2 。每一秒,对于所有下标 0 <= i < nums1.length ,nums1[i] 的值都增加 nums2[i] 。操作 完成后 ,你可以进行如下操作:
- 解法
- DP+贪心+正难则反:
- 第 1 步:
- 每个 nums1[i] 置为 0,超过一次不如仅最后一次置为 0,
- 可知对于 nums1[i] 一样大,且不会影响其他 nums1,
- 因此时间最多就是 nums1.len、超过则无意义,
- 第 2 步:
- 问题转化为经过最少 s 秒且 s <= nums1.len,使得 nums3 = nums2[x]*(s-1) + nums2[y]*(s-2) + … + nums2[z]*0 + nums1[a] + …,nums3.len = nums1.len
- nums3 总和 sum(nums3) 小于等于 x 时,最小的 s 就是答案,否则答案就是 -1,
- 同时不可能推出 s 单调性,因此无法二分答案,
- 第 3 步:
- 正面直接求最小值无法想到什么贪心策略,如果使用 DP 则第 j+1 秒会影响前 j 秒的数据,因为每秒每个元素会加上 nums2,不满足无后效性,
- 正难则反:
- 求经过 s 秒最多可以减少多少
- 总数 sum(nums1) + s*sum(nums2) 减去即可
- 第 4 步:
- 动规状态:dp[i][j] 为前 i 个数经过 j 秒最多可以减少多少,注意 i>=j,
- 初始化 dp[i][0]=0,即前 i 个数不经过任何时间则无法减少
- 第 5 步:
- 转移方程:dp[i][j]=max(dp[i-1][j], dp[i-1][j-1] + nums1[i-1]+j*nums2[i-1]),
- 即第 i 个数经过 j 秒是否删除的最大值,取决于是否需要再第 j 秒清理掉第 i 个元素
- 此时 DP 无后效性,因为第 i+1 个数不会影响前 i 个数的更新,
- 同时需要满足减少 j 个元素的最大值、等于减少前(i-1 个元素中选 j-1 个元素)的最大值加第 i 个元素,
- 可以观察减少的是 nums1[i-1]+j*nums2[i-1],由于前 j 秒等价于选 j 个元素,此时 nums1 顺序无所谓,j 固定升序、保证 j*nums2[i-1] 最大需要使 nums2 升序(nums1 跟随排序)
- 第 6 步:
- 最后结果就是枚举秒数 j=[0,nums1.len],sum(nums1) + j * sum(nums2) - dp[nums1.len][j] <= x,找到最小的 j,没有则返回 -1
- 空间压缩:由于 dp[i][j] 仅与 dp[i-1][j]、dp[i-1][j-1] 有关,因此可以使用一维 dp[j] 倒序处理
- 时间复杂度:O(n ^ 2),空间复杂度:O(n)
- 代码
/*** DP+贪心+正难则反:** 第 1 步:* 每个 nums1[i] 置为 0,超过一次不如仅最后一次置为 0,* 可知对于 nums1[i] 一样大,且不会影响其他 nums1,* 因此时间最多就是 nums1.len、超过则无意义,** 第 2 步:* 问题转化为经过最少 s 秒且 s <= nums1.len,使得 nums3 = nums2[x]*(s-1) + nums2[y]*(s-2) + ... + nums2[z]*0 + nums1[a] + ...,nums3.len = nums1.len* nums3 总和 sum(nums3) 小于等于 x 时,最小的 s 就是答案,否则答案就是 -1,* 同时不可能推出 s 单调性,因此无法二分答案,** 第 3 步:* 正面直接求最小值无法想到什么贪心策略,如果使用 DP 则第 j+1 秒会影响前 j 秒的数据,因为每秒每个元素会加上 nums2,**不满足无后效性**,* 正难则反:* * 求经过 s 秒最多可以减少多少* * 总数 sum(nums1) + s*sum(nums2) 减去即可** 第 4 步:* 动规状态:dp[i][j] 为前 i 个数经过 j 秒最多可以减少多少,注意 i>=j,* 初始化 dp[i][0]=0,即前 i 个数不经过任何时间则无法减少** **第 5 步**:* 转移方程:dp[i][j]=max(dp[i-1][j], dp[i-1][j-1] + nums1[i-1]+j*nums2[i-1]),* * 即第 i 个数经过 j 秒是否删除的最大值,取决于是否需要再第 j 秒清理掉第 i 个元素* * **此时 DP 无后效性**,因为第 i+1 个数不会影响前 i 个数的更新,* * 同时需要满足减少 j 个元素的最大值、等于减少前(i-1 个元素中选 j-1 个元素)的最大值加第 i 个元素,* * 可以观察减少的是 nums1[i-1]+j*nums2[i-1],由于前 j 秒等价于选 j 个元素,此时 nums1 顺序无所谓,**j 固定升序、保证 j*nums2[i-1] 最大需要使 nums2 升序(nums1 跟随排序)**** 第 6 步:* 最后结果就是枚举秒数 j=[0,nums1.len],sum(nums1) + j * sum(nums2) - dp[nums1.len][j] <= x,找到最小的 j,没有则返回 -1* 空间压缩:由于 dp[i][j] 仅与 dp[i-1][j]、dp[i-1][j-1] 有关,因此可以使用一维 dp[j] 倒序处理* 时间复杂度:O(n ^ 2),空间复杂度:O(n)*/public int minimumTime(List<Integer> nums1, List<Integer> nums2, int x) {// 判空与异常if (nums1 == null || nums2 == null || nums1.size() != nums2.size() || nums1.size() <= 0) {return -1;}int n = nums1.size();// 求总和int sumNums1 = nums1.stream().mapToInt(Integer::intValue).sum();int sumNums2 = nums2.stream().mapToInt(Integer::intValue).sum();
// System.out.println(sumNums1);
// System.out.println(sumNums2);// j 固定升序、保证 j*nums2[i-1] 最大需要使 nums2 升序(nums1 跟随排序)List<Pair<Integer, Integer>> numsPair = new ArrayList<>(n);for (int i = 0; i < n; i++) {numsPair.add(new Pair<>(nums2.get(i), nums1.get(i)));}Collections.sort(numsPair, (o1, o2) -> o1.getKey() - o2.getKey());
// System.out.println(numsPair);// 动规状态:dp[i][j] 为前 i 个数经过 j 秒最多可以减少多少,注意 i>=j,初始化 dp[i][0]=0,即前 i 个数不经过任何时间则无法减少,空间压缩掉 iint[] dp = new int[n + 1];// 转移方程:dp[i][j]=max(dp[i-1][j], dp[i-1][j-1] + nums1[i-1]+j*nums2[i-1]),for (int i = 1; i < n + 1; i++) {// 空间压缩,一维 dp[j] 倒序处理for (int j = i; j >=1; j--) {dp[j] = Math.max(dp[j], dp[j-1] + numsPair.get(i-1).getValue() + j * numsPair.get(i-1).getKey());}}
// AlgorithmUtils.systemOutArray(dp);int res = -1;// 枚举秒数 j=[0,nums1.len],sum(nums1) + j * sum(nums2) - dp[nums1.len][j] <= x,找到最小的 j,没有则返回 -1for (int j = 0; j <= n; j++) {if (sumNums1 + j * sumNums2 - dp[j] <= x) {res = j;break;}}return res;}
相关文章:
)
Leetcode 第 110 场双周赛 Problem D 2809. 使数组和小于等于 x 的最少时间(DP+贪心+正难则反)
Leetcode 第 110 场双周赛 Problem D 2809. 使数组和小于等于 x 的最少时间(DP 好题)题目 给你两个长度相等下标从 0 开始的整数数组 nums1 和 nums2 。每一秒,对于所有下标 0 < i < nums1.length ,nums1[i] 的值都增加 num…...
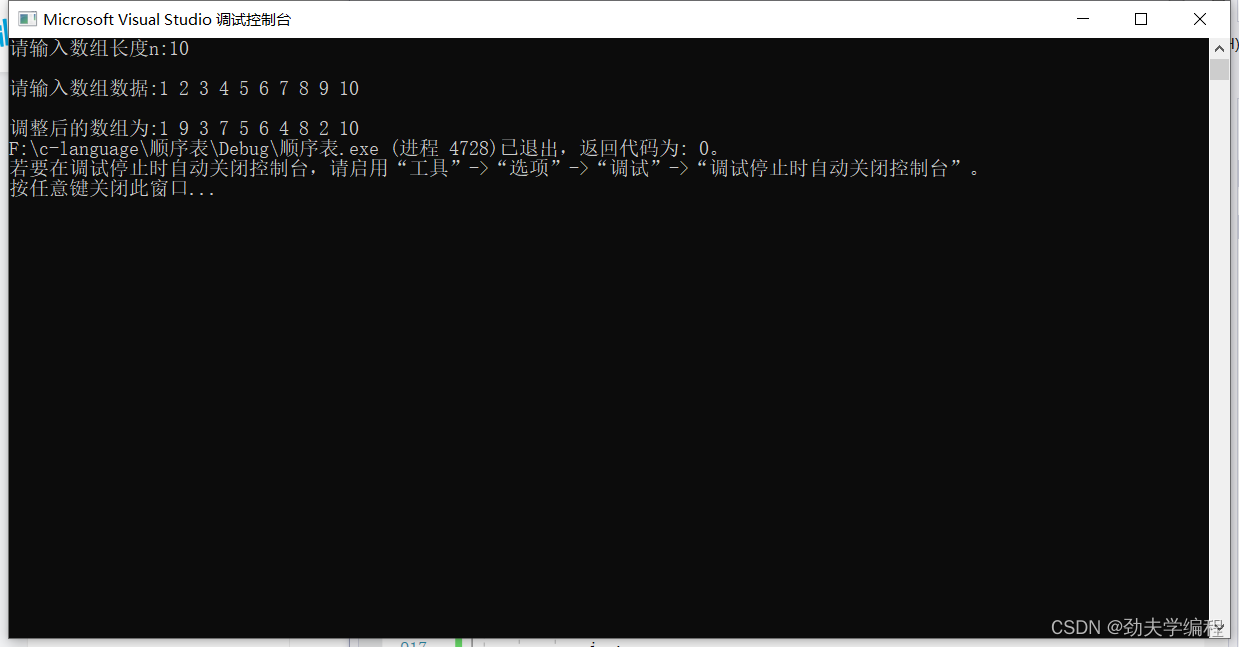
已知数组A[1..n]中元素类型为非负整数,设计算法将其调整为左右两部分,左边所有为奇数,右边所有为偶数,并要求算法的时间复杂度为O(n)
//左边奇数右边偶数 void Swap(int* a, int* b) {int tmp *b;*b *a;*a tmp; } void LeftRight(int arr[],int n) {int i 0;int j n - 1;while(i<j){if (arr[i] % 2 0 && arr[j] % 2 1) {Swap(&arr[i], &arr[j]);i;j--;}else if (arr[i] % 2 1 &…...
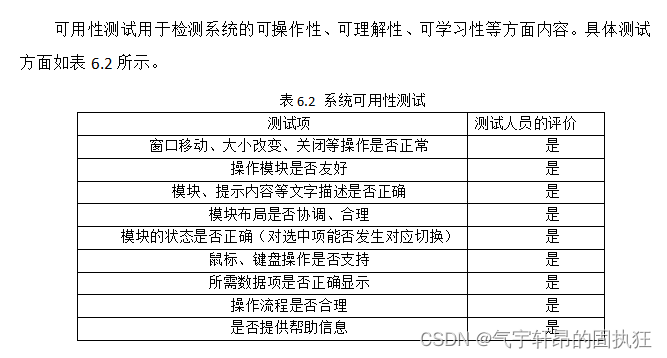
ssm+vue的罪犯信息管理系统(有报告)。Javaee项目,ssm vue前后端分离项目。
演示视频: ssmvue的罪犯信息管理系统(有报告)。Javaee项目,ssm vue前后端分离项目。 项目介绍: 采用M(model)V(view)C(controller)三层体系结构&…...

Java/Android 各类型数据构造和各类型数据解析
Java/Android 各类型数据构造和各类型数据解析 1.如何构造/解析{"key":"value","key":"value","key":"value"}jsonString1)json解析2)fastjson解析3)Gson解析4)遍历key值解析2.如何构造/解析[{"key&q…...
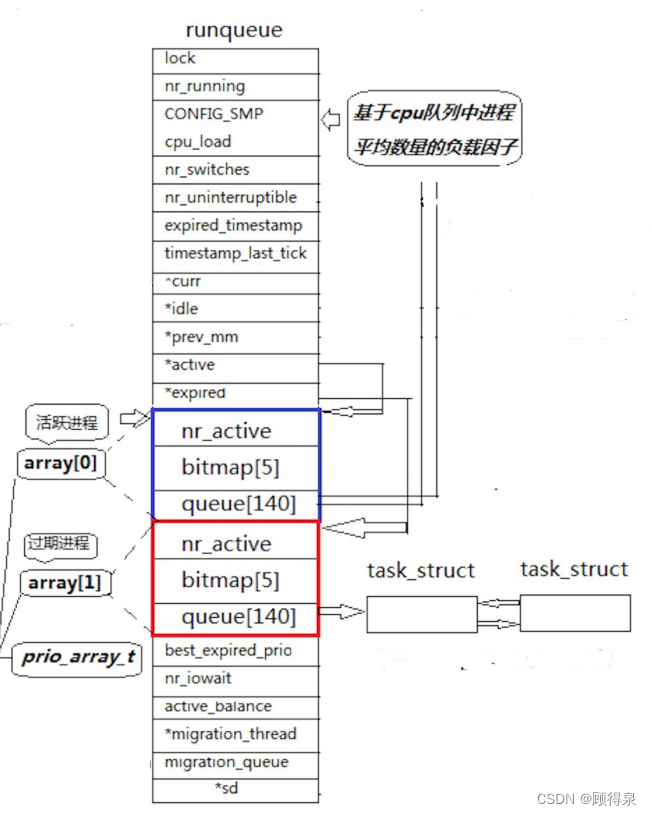
Linux系统---环境变量+内核进程调度队列(选学)
顾得泉:个人主页 个人专栏:《Linux操作系统》 《C/C》 《LeedCode刷题》 键盘敲烂,年薪百万! 一、环境变量 1.基本概念 环境变量(environment variables)一般是指在操作系统中用来指定操作系统运行环境的一些参数,…...

Kubernetes 使用插件扩展 kubectl
例子演示 编写 kubectl-foo ,拷贝至 /usr/local/bin/ #!/bin/bash# 可选的参数处理 if [[ "$1" "version" ]] thenecho "1.0.0"exit 0 fi# 可选的参数处理 if [[ "$1" "config" ]] thenecho $KUBECONFIGexit…...

前端面试题09
74、定义类的方法有哪些 在JavaScript中,定义类的方法有以下几种方式: 1.使用函数声明: function MyClass() {// constructor } MyClass.prototype.methodName function() {// method body };2.使用类的方法缩写(ES6引入&…...

网站更换IP的四大注意事项
1.对网站当中的数据进行备份 网站更换IP时可以将页面的数据库文件和站点文件通过下载工具在本地完成备份。 2.更换解析域名 从站点域名管理后台当中更换域名地址,改为新的IP地址。 3.确保IP安全 在用户更换IP前一定要确定IP是否安全,一旦IP存在不良…...
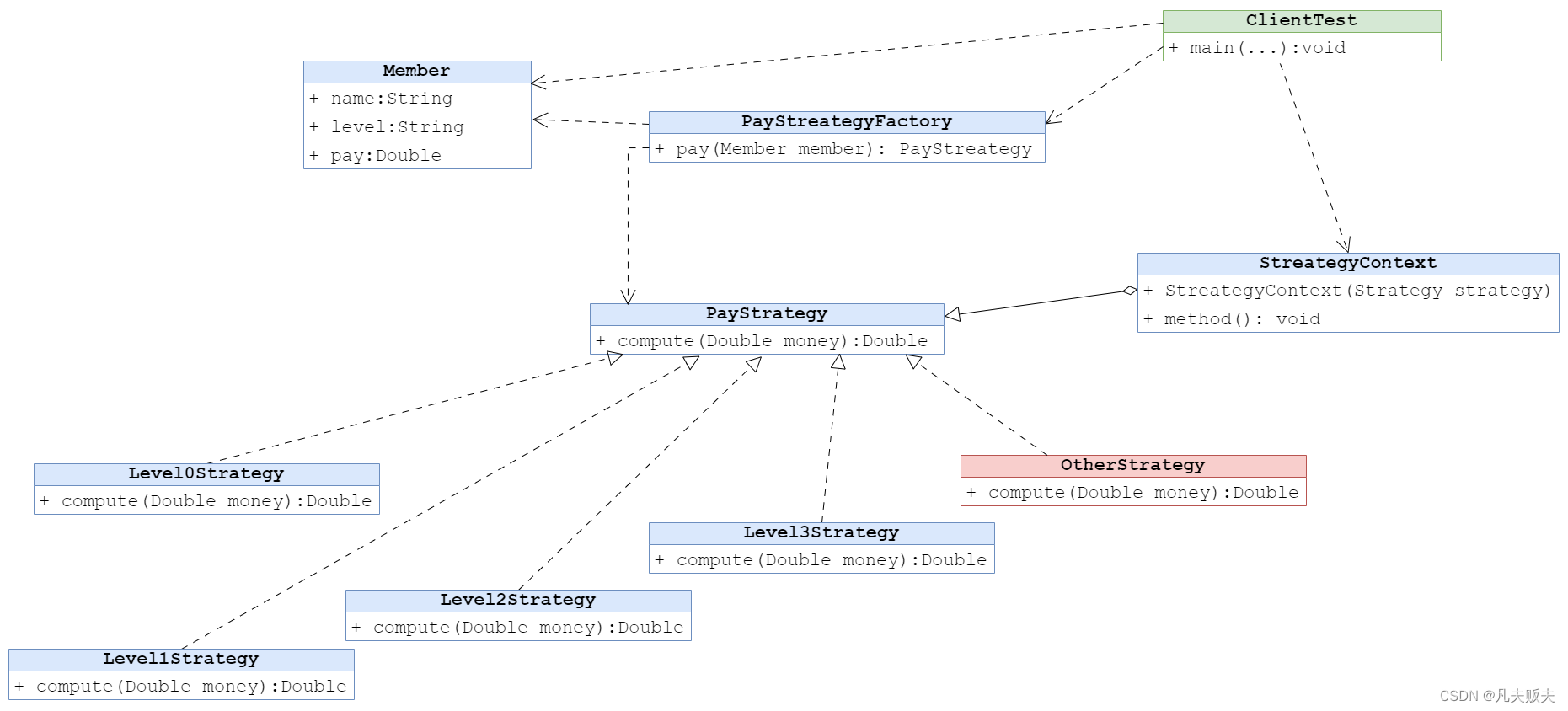
策略模式与简单工厂模式:终结if-else混乱,让代码更清爽
阅读建议 嗨,伙计!刷到这篇文章咱们就是有缘人,在阅读这篇文章前我有一些建议: 本篇文章大概4500多字,预计阅读时间长需要5分钟。本篇文章的实战性、理论性较强,是一篇质量分数较高的技术干货文章&#x…...
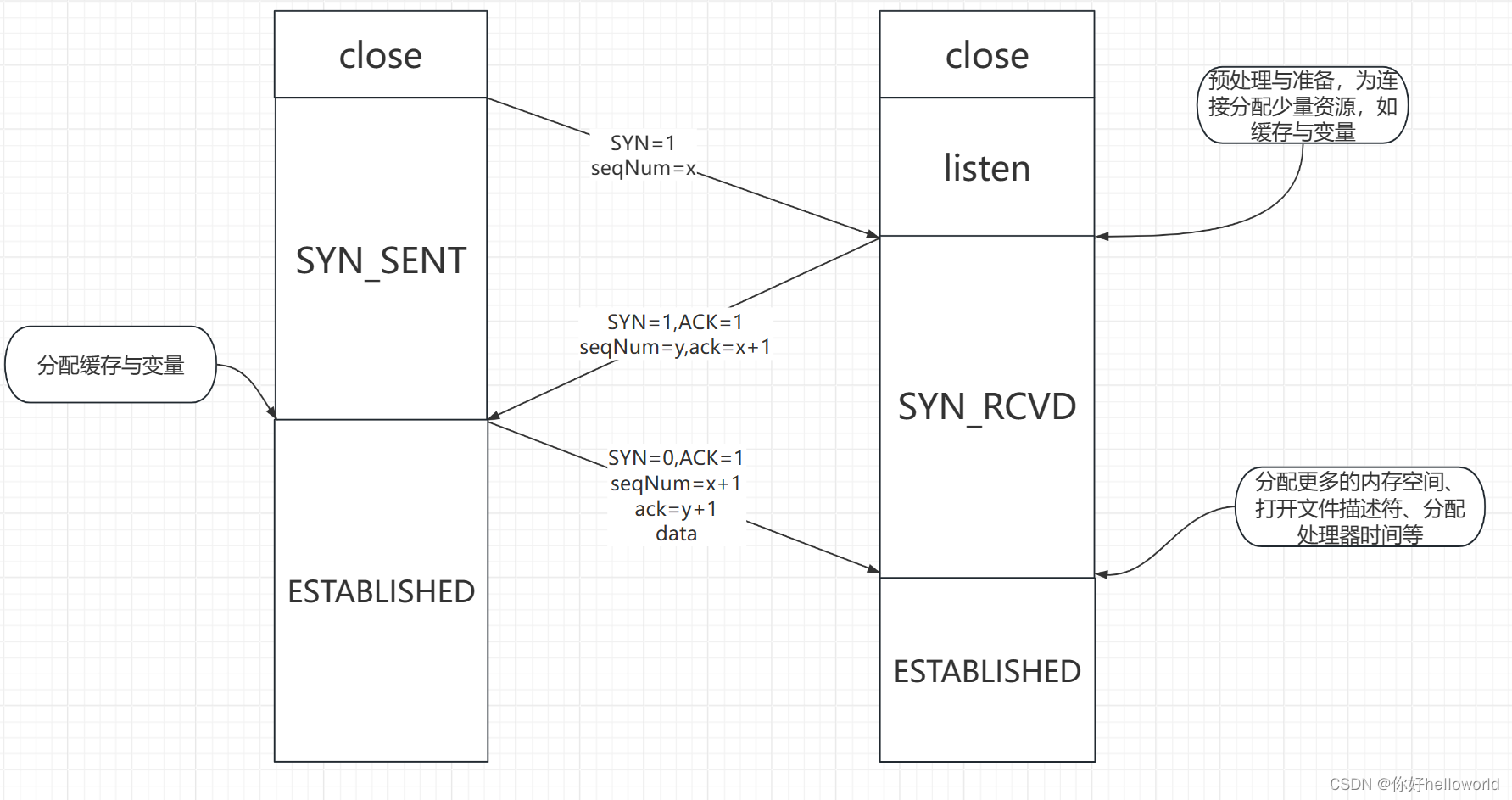
TCP三次握手过程
什么是TCP tcp是一个面向连接的、可靠的、基于字节流的传输层通信协议 面向连接:TCP连接是一对一的,不能实现一对多或多对一,TCP在通信前要首先建立连接,连接成功后才能开始进行通信可靠的:TCP连接要保证通信过程的可靠…...

04-配置远程仓库的SSH免密登陆
配置SSH免密登录 配置步骤 创建好的远程仓库也可以使用SSH的方式进行访问,但如果没有配置公钥会有警告 第一步: 删除用户家目录下的.ssh目录,如果没有该目录或者该目录下已经有密钥了就不用执行该操作 #进入当前用户的家目录,删除.ssh 目录 LayneLAPTOP-Layne MINGW64 ~ $ r…...
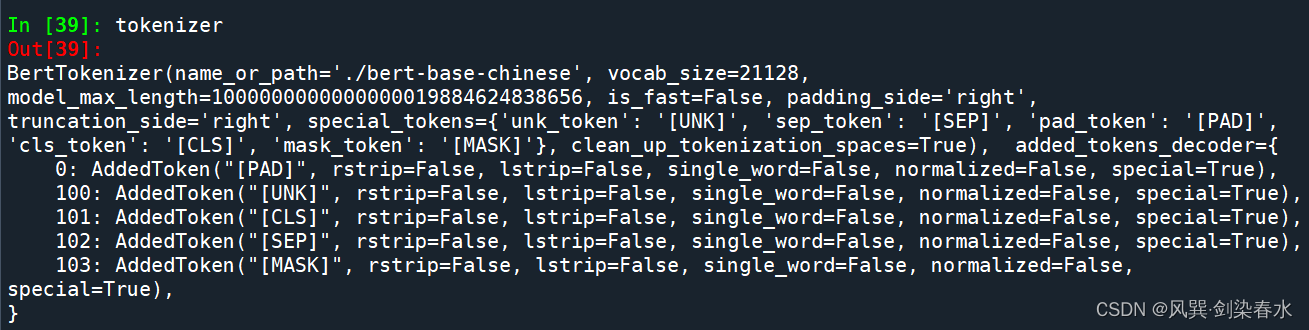
【中文编码】利用bert-base-chinese中的Tokenizer实现中文编码嵌入
最近接触文本处理,查询了一些资料,记录一下中文文本编码的处理方法吧。 先下载模型和词表:bert-base-chinese镜像下载 如下图示,下载好的以下文件均存放在 bert-base-chinese 文件夹下 1. 词编码嵌入简介 按我通俗的…...
一文解决msxml3.dll文件缺失问题,快速修复msxml3.dll
在了解问题之前,我们必须首先清楚msxml3.dll到底是什么。DLL(Dynamic Link Libraries)文件是Windows操作系统使用的一个重要组成部分,用于存储执行特定操作或任务的代码和数据。msxml3.dll为Windows系统提供处理XML文档的功能。如…...

《React 知识点》第一篇 大括号使用{}
简介 大括号 " {} "可以用于包裹JavaScript的表达式或语句。以便在jsx中动态生成内容。 插入变量与表达式 function expressionTest() {const name "变量测试";return (<p><div>{name}</div><div>表达式 210 {2 100}</div…...
: 位移提交)
kafka入门(二): 位移提交
位移提交: Kafka的每条消息都有唯一的 offset, 用来表示消息在分区中对应的位置。有的也称之为 “偏移量”。 消费者每次在 poll() 拉取消息,它要返回的是还没有消费过的消息集, 因此,需要记录上一次消费时的消费位…...

PG时间计算
PG数据库,时间计算使用场景总结 日期之差 --**获取秒差** SELECT round(date_part(epoch, TIMESTAMP 2019-05-05 12:11:20 - TIMESTAMP 2019-05-05 10:10:10)); --**获取分钟差** SELECT round(date_part(epoch, TIMESTAMP 2019-05-05 12:11:20 - TIMESTAMP 20…...
基于51单片机的交通灯_可调时间_夜间+紧急模式
51单片机交通灯 1 讲解视频:2 功能要求3 仿真图:4 原理图PCB5 实物图6 程序设计:7 设计报告8 资料清单(提供资料清单所有文件):设计资料下载链接: 51单片机简易交通灯_可调时间_夜间紧急 仿真代…...

网络通信原理,进制转化总结
来源,做个笔记,讲的还蛮清楚通信原理-2.5 数据封装与传输05_哔哩哔哩_bilibili ip地址范围...

西南科技大学(数据结构A)期末自测练习三
一、填空题(每空1分,共10分) 1、为解决计算机主机与打印机之间速度不匹配的问题,通常设置一个打印数据缓冲区。主机将要输出的数据依次写入缓冲区,打印机则依次从缓冲区中取出数据,则该换缓冲区的逻辑结构…...
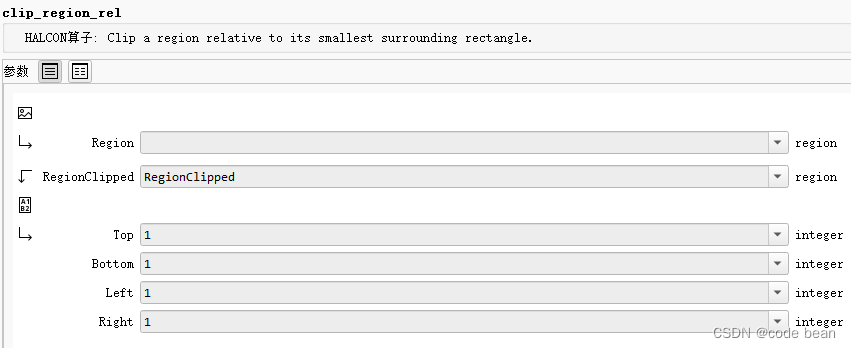
【halcon】裁剪
前言 目前我遇到的裁剪相关的函数都是以clip打头的函数。一共4个: clip_end_points_contours_xldclip_contours_xldclip_regionclip_region_rel 前面两个是对轮廓的裁剪。 后面是对区域的裁剪。 裁剪轮廓的两端 clip_end_points_contours_xld 用于实现裁剪XLD…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...

电脑桌面太单调,用Python写一个桌面小宠物应用。
下面是一个使用Python创建的简单桌面小宠物应用。这个小宠物会在桌面上游荡,可以响应鼠标点击,并且有简单的动画效果。 import tkinter as tk import random import time from PIL import Image, ImageTk import os import sysclass DesktopPet:def __i…...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...
