如何编写测试用例?
编写测试用例流程
1、确定测试目标:首先,需要明确测试目标,即测试人员需要测试什么,这有助于测试人员了解需要测试哪些方面,以及如何测试。
2、识别测试场景:在确定测试目标后,测试人员需要识别测试场景,即根据测试目标来确定哪些情况需要被测试。例如,对于一个购物网站,测试场景可能包括注册、登录、搜索、结账等。
3、定义测试用例:对于每个测试场景,测试人员需要编写一系列测试用例。测试用例应该具有清晰的目标、输入、预期输出、步骤和结果。这些测试用例可以作为测试人员在执行测试时的指导。
4、确定测试数据:对于每个测试用例,需要明确需要的测试数据,例如输入的用户名、密码等。测试人员需要准备好测试数据,以便在执行测试时使用。
5、设计测试套件:在编写测试用例后,测试人员需要将它们组合成测试套件。测试套件可以按照模块、功能或场景来组织。
6、执行测试用例:测试人员需要按照测试用例执行测试,记录测试结果。在执行测试时,需要注意记录每个测试用例的结果,以便后续进行分析和修复缺陷。
7、分析测试结果:在执行测试后,测试人员需要分析测试结果,以确定是否达到了测试目标。如果发现了缺陷,需要将其记录下来,并通知开发人员进行修复。
8、汇报测试结果:在分析测试结果后,测试人员需要汇报测试结果,包括测试的覆盖率、问题的数量和严重程度、测试的有效性等方面。测试报告应该清晰、简洁、易于理解和阅读,同时应该包含必要的统计数据和图表。
编写用例考虑要素
1、测试目标:测试用例应该明确测试的目标,包括测试的功能、特性、性能等方面。
2、测试场景:测试用例应该基于测试场景编写,测试场景是指软件系统的一个部分或功能,测试用例需要覆盖测试场景中可能出现的各种情况,例如边界情况、异常情况等。
3、测试用例的组成:测试用例应该具有清晰的目标、输入、预期输出、步骤和结果等要素。
4、测试数据:测试用例需要使用特定的测试数据,测试数据应该具有代表性,能够充分覆盖各种测试场景和测试用例。
5、测试套件:测试用例可以按照功能、模块、场景等进行分类,并组成一个测试套件,以便管理和执行测试。
6、测试的覆盖率:测试用例需要覆盖系统的不同方面和不同的场景,从而确保测试的全面性和准确性。
7、执行顺序:测试用例应该按照特定的顺序执行,以避免测试顺序对测试结果的影响。
8、测试结果:测试用例执行后应该记录测试结果,包括成功或失败的信息,以及测试用例的执行时间等。
9、可重复性:测试用例应该具有可重复性,即可以重复执行并获得相同的结果,从而确保测试的可靠性和稳定性。
10、测试环境:测试用例需要在特定的测试环境中执行,测试环境应该与实际环境尽可能接近,以确保测试的准确性和可靠性。
11、测试工具:测试用例需要使用特定的测试工具,例如自动化测试工具、性能测试工具、安全测试工具等,以提高测试效率和准确性。
12、测试人员的技能和经验:测试用例的编写需要测试人员具有一定的技能和经验,包括软件测试的基本知识和测试方法、测试工具的使用等方面。
13、测试用例的评审:测试用例编写后应该进行评审,以确保测试用例的准确性和完整性,同时评审过程也可以发现测试用例中的问题和改进点。
14、测试用例的版本管理:测试用例需要进行版本管理,以记录测试用例的变更历史和版本信息,方便管理和维护测试用例。
15、测试用例的复用性:测试用例可以被多次使用,例如在不同版本的软件中或在不同的测试场景中,测试用例的复用性可以提高测试效率和准确性。
相关文章:

如何编写测试用例?
编写测试用例流程 1、确定测试目标:首先,需要明确测试目标,即测试人员需要测试什么,这有助于测试人员了解需要测试哪些方面,以及如何测试。 2、识别测试场景:在确定测试目标后,测试人员需要识…...

5.排序算法之二:选择排序
选择排序(select sort)在无序列表中,把无序列表分成有序区(刚开始有序区元素个数为0)和无序区(刚开始无序区元素个数为n),循环n-1趟,每一趟找到最小或最大的那个元素&…...

Ubuntu18系统安装:node及node版本管理工具nvm部署前端项目
注意在安装之前先安装好Git 如何在Ubuntu 上安装Git与入门教程_ubuntu安装git_飞鹰雪菲的博客-CSDN博客 1、把nvm远程镜像克隆到指定目录 git clone https://gitee.com/mirrors/nvm 1.1在终端指定的文件夹下 drciZwz91oq31508figapkas0Z:~/qiang/tools$ git clone https://…...
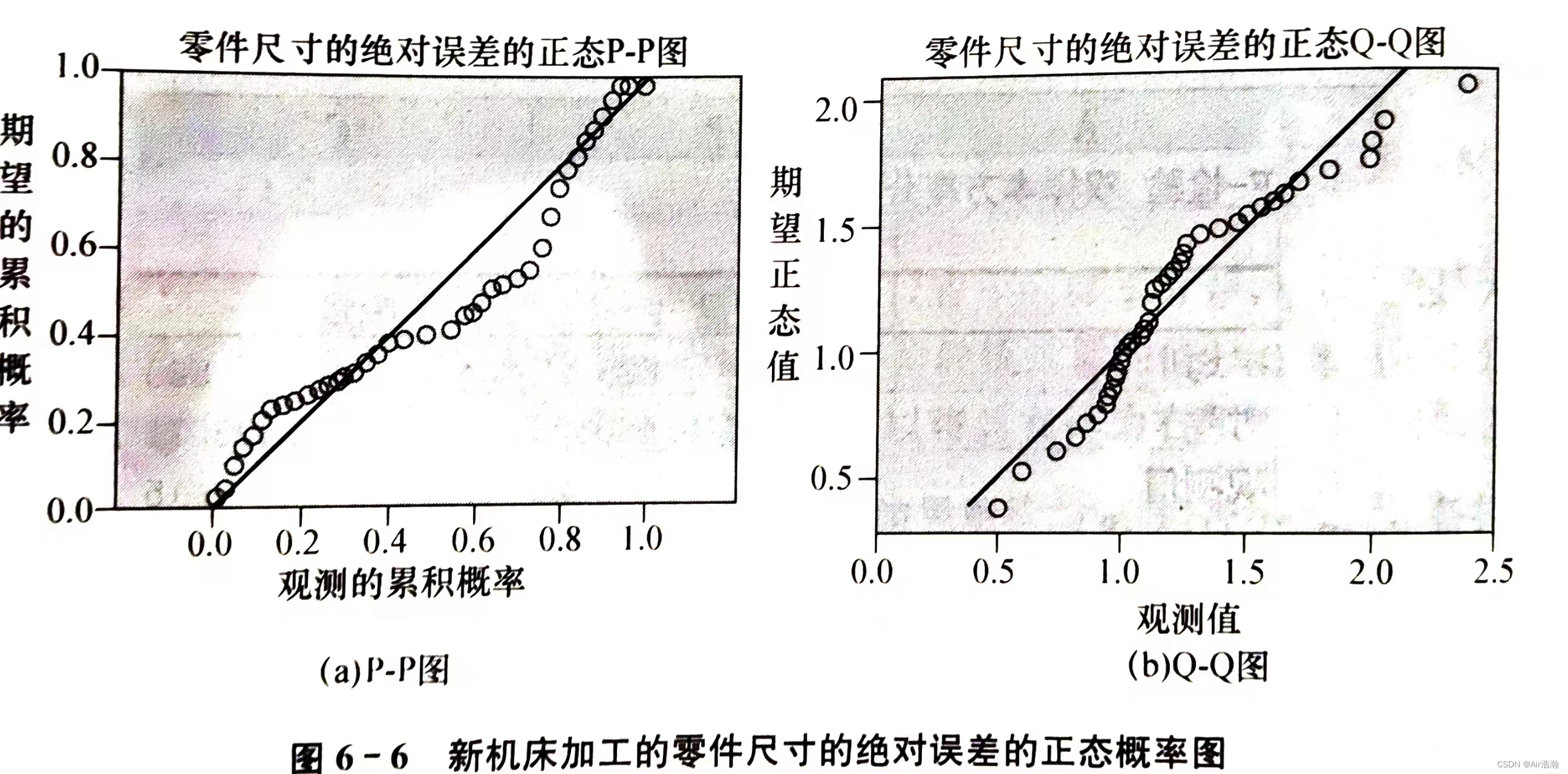
统计学 假设检验
文章目录假设检验假设检验的基本原理提出假设作出决策表述决策结果一个总体参数的检验总体均值的检验总体比例的检验总体方差的检验两个总体参数的检验两个总体均值之差的检验两个总体比例之差的检验两个总体方差比的检验总体分布的检验正态性检验的图示法Shapiro-Wilk 和 K-S …...
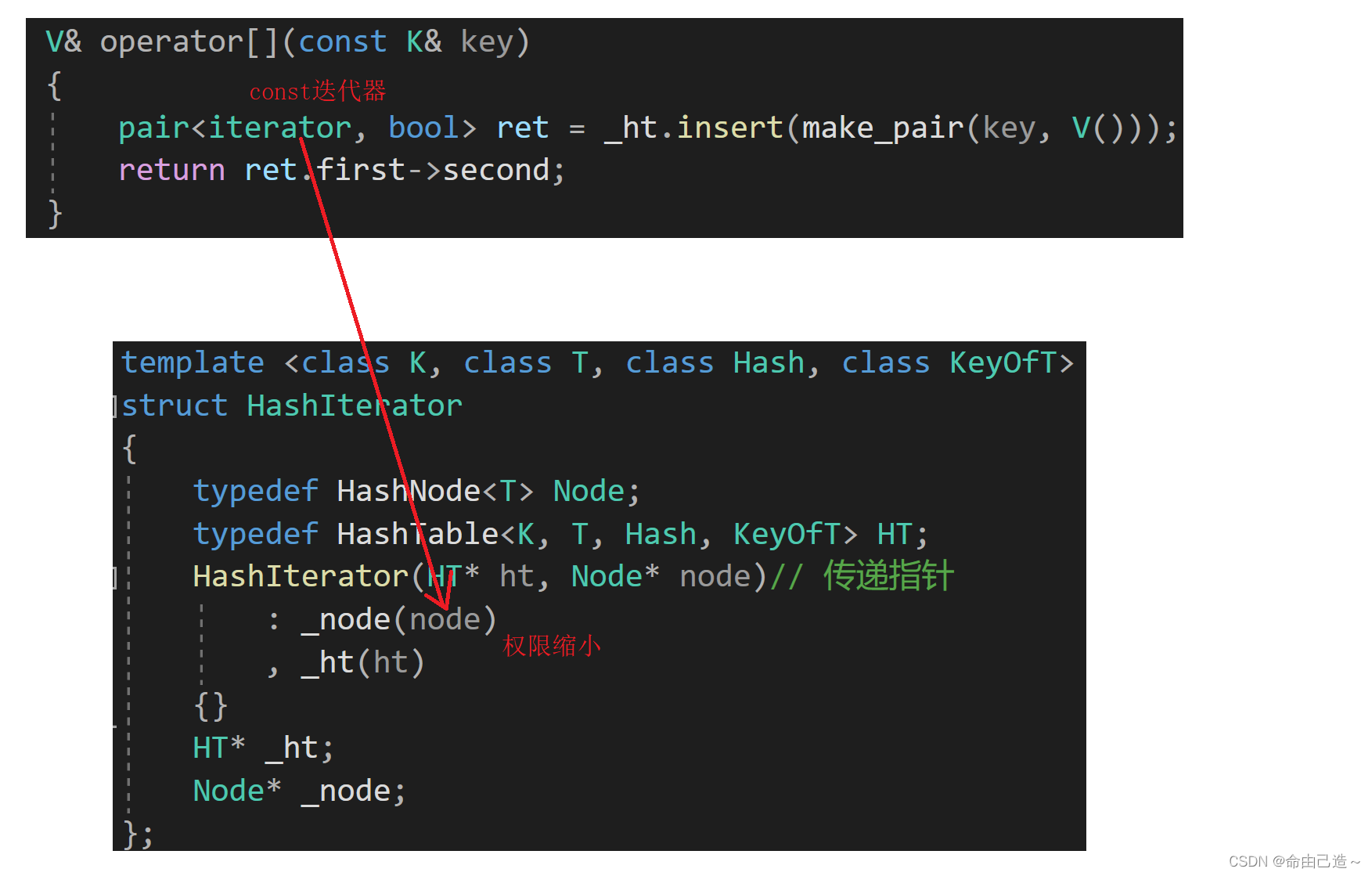
【C++】哈希
哈希一、unordered系列关联式容器二、哈希原理2.1 哈希映射2.2 哈希冲突2.2.1 闭散列—开放地址法2.2.2 代码实现2.2.3 开散列—拉链法2.2.4 代码实现三、哈希封装unordered_map/unordered_set3.1 基本框架3.2 迭代器实现3.2.3 operator*和operator->和operator!3.2.4 opera…...
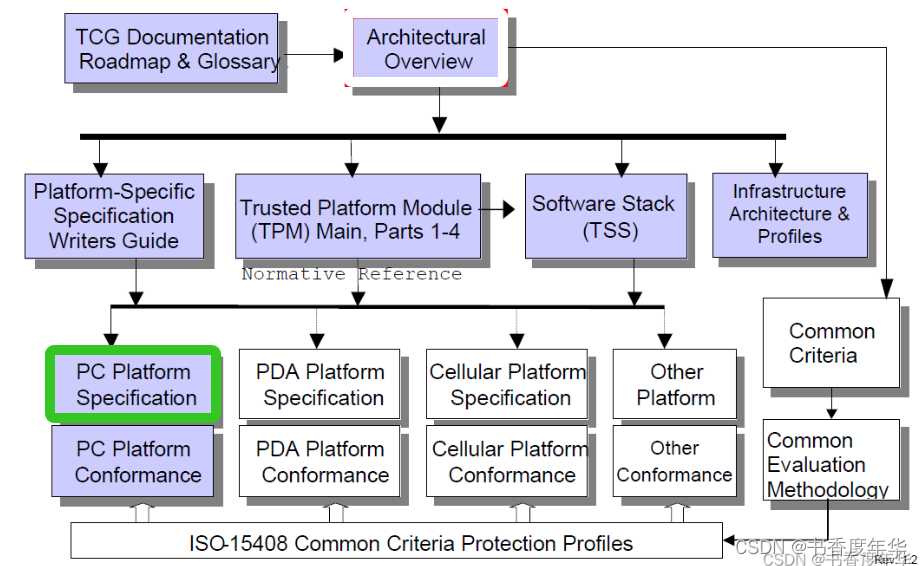
「TCG 规范解读」PC 平台相关规范(3)
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...
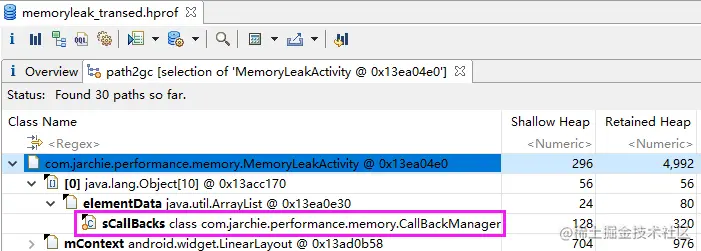
这篇教你搞定Android内存优化分析总结
一、内存优化概念1.1 为什么要做内存优化?内存优化一直是一个很重要但却缺乏关注的点,内存作为程序运行最重要的资源之一,需要运行过程中做到合理的资源分配与回收,不合理的内存占用轻则使得用户应用程序运行卡顿、ANR、黑屏&…...

概率论与数理统计期末小题狂练 11-12两套,12-13-1
11-12第一学期A1 略。2 X服从正态分布N(0,1),X^2服从卡方分布。又考查了卡方分布均值和方差公式。一开始如果对本题无从下手,大概是没看出来是什么分布。3 第二小空本身也可以作为一个结论。4 考查切比雪夫不等式&…...

golang对字符串的处理操作 如何正确理解 rune byte和string
fmt.Printf相关参数介绍 先来看代码的演示 package mainimport ("fmt""unicode/utf8" )func main() {s:"我爱中国人haha!"fmt.Println(len(s))//20个字节 一个中文三个字节 1541fmt.Print("\n echo byte \n")for k,v: range []byte(…...
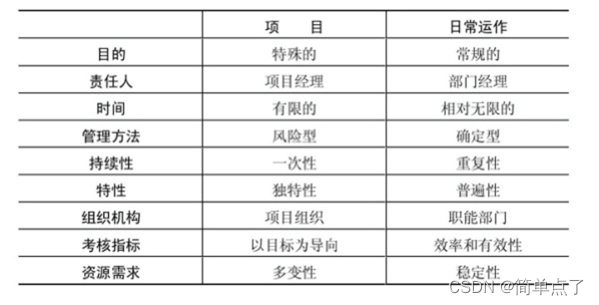
软件项目管理简答题复习(1)
1.项目:创造唯一的产品,唯一的服务临时性的努力 2.项目特征:不可见性,复杂性,一致性,变更性,特殊性 3.项目和日常活动的区别? 项目具有特殊性,负责人是项目经理&#…...
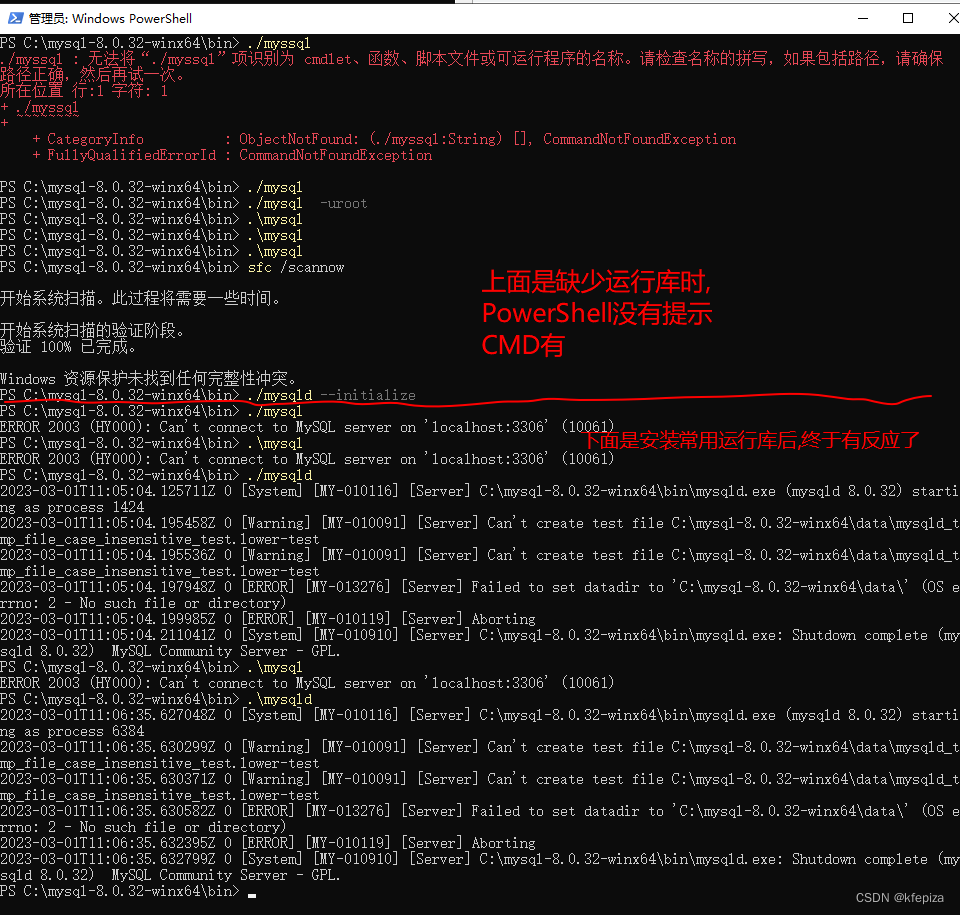
云Windows Server 2022 Datacenter 安装MySQL8解压缩版 mysql-8.0.32-winx64 230301记录
MySQL Community Downloads MySQL社区版压缩包下载地址 https://dev.mysql.com/downloads/mysql/ 解压到了C盘 没打算设置环境变量 右键点击开始 或 winx 以管理员身份打开 PowerShell 进入到安装目录下的 bin 目录 可以输入cd 后, 拖动 bin 文件夹到控制台&…...

如何使用BeaconEye监控CobaltStrike的Beacon
关于BeaconEye BeaconEye是一款针对CobaltStrike的安全工具,该工具可以扫描正在运行的主动CobaltStrike Beacon。当BeaconEye扫描到了正在运行Beacon的进程之后,BeaconEye将会监控每一个进程以查看C2活动。 工作机制 BeaconEye将会扫描活动进程或Mini…...
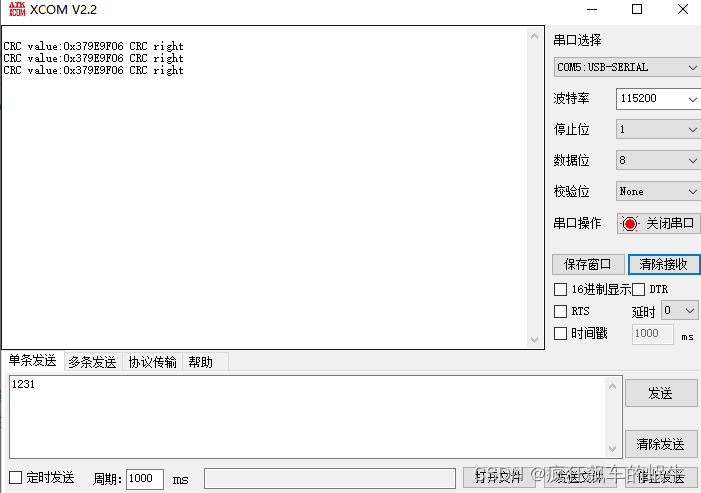
STM32开发(17)----CubeMX配置CRC
CubeMX配置CRC前言一、什么是CRC?二、实验过程1.STM32CubeMX配置2.代码实现重载printf3.实验结果总结前言 本章介绍使用STM32CubeMX对CRC进行配置的方法,CRC的目的是保证数据的完整性,所有的STM32芯片都内置了一个硬件的CRC计算模块…...
【MySQL】基础操作:登录、访问、退出和卸载
一、MySQL简介 MySQL数据库最初是由瑞典MySQL AB公司开发,2008年1月16号被Sun公司收购。2009年,SUN又被Oracle收购。MySQL是目前IT行业最流行的开放源代码的数据库管理系统,同时它也是一个支持多线程、高并发、多用户的关系型数据库管理系统。…...
)
【算法经典题集】递推(持续更新~~~)
😽PREFACE🎁欢迎各位→点赞👍 收藏⭐ 评论📝📢系列专栏:算法经典题集🔊本专栏涉及到的知识点或者题目是算法专栏的补充与应用💪种一棵树最好是十年前其次是现在递推简单的斐波那契…...

mysql兼容性验证
MySQL是一个关系型数据库管理系统。 一、安装启动 安装mysql相关软件包 yum install mysql-server 启动mysql服务 systemctl start mysqld systemctl status mysqld mysql数据库启动失败问题汇总: <问题1>、start mysqld显示失败,如下所示&…...

C++回顾(五)—— 构造函数和析构函数
5.1 构造和析构 5.1.1 构造函数 (1)定义 1)C中的类可以定义与类名相同的特殊成员函数,这种与类名相同的成员函数叫做构造函数;2)构造函数在定义时可以有参数;3)没有任何返回类型的…...

嵌入式学习笔记——概述
嵌入式系统概述前言“嵌入式系统”概念1.是个啥?2.可以干啥?3.有哪些入坑方向?4.入坑后可以有多少薪资?单片机1.什么是单片机?2.架构简介3.基于ARM架构的单片机结构简介总结前言 断更很长时间了,写博客确实…...
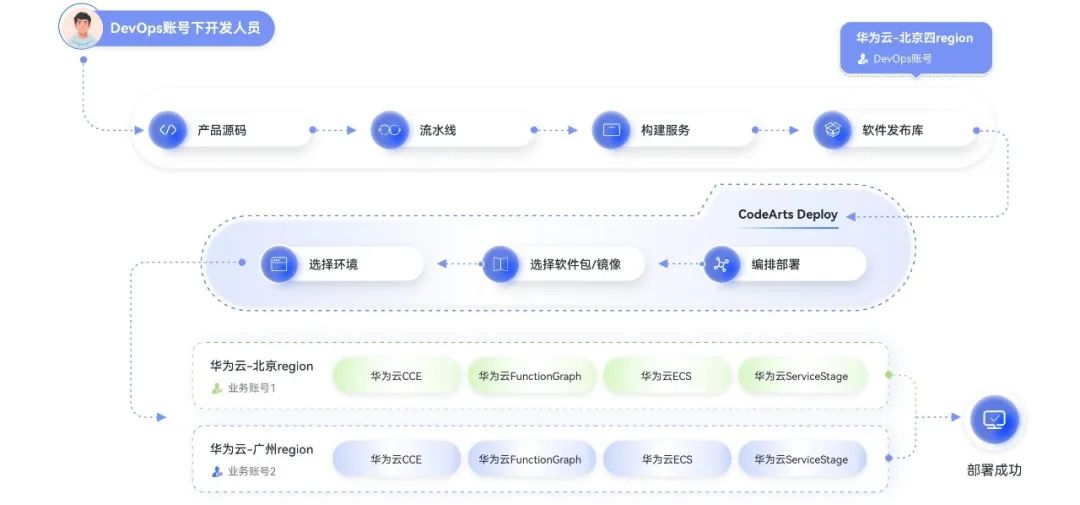
化繁为简高效部署 华为云发布部署服务CodeArts Deploy
随着互联网、数字化的发展,公司机构与各类企业往往需要进行大量频繁的软件部署,部署设备类型多样,如:本地机器、云上裸金属服务器、云上虚拟机与容器等。面对多种部署模式、分布式复杂运行环境,如何用最短时间、高质…...

注意力机制详解系列(四):混合注意力机制
👨💻作者简介: 大数据专业硕士在读,CSDN人工智能领域博客专家,阿里云专家博主,专注大数据与人工智能知识分享。 🎉专栏推荐: 目前在写CV方向专栏,更新不限于目标检测、OCR、图像分类、图像分割等方向,目前活动仅19.9,虽然付费但会长期更新,感兴趣的小伙伴可以…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...

二叉树-144.二叉树的前序遍历-力扣(LeetCode)
一、题目解析 对于递归方法的前序遍历十分简单,但对于一位合格的程序猿而言,需要掌握将递归转化为非递归的能力,毕竟递归调用的时候会调用大量的栈帧,存在栈溢出风险。 二、算法原理 递归调用本质是系统建立栈帧,而非…...
