统计学 假设检验
文章目录
- 假设检验
- 假设检验的基本原理
- 提出假设
- 作出决策
- 表述决策结果
- 一个总体参数的检验
- 总体均值的检验
- 总体比例的检验
- 总体方差的检验
- 两个总体参数的检验
- 两个总体均值之差的检验
- 两个总体比例之差的检验
- 两个总体方差比的检验
- 总体分布的检验
- 正态性检验的图示法
- Shapiro-Wilk 和 K-S 正态性检验
- 总结
假设检验
假设检验的基本原理
提出假设
假设检验:先对总体提出某种假设(例如对总参数提出一个假设值),然后利用样本信息判断这一假设是否成立
原假设:也称零假设,通常是研究者想搜集证据予以推翻的假设,记为H0H_{0}H0 ;原假设表达的含义是指参数没有变化、变量之间没有联系或总体分布与一理论分布并无差异,所以常有===。设参数的假设值为μ0\mu_{0}μ0,原假设常写成 H0:μ=μ0;H0:μ≥μ0;H0:μ≤μ0H_{0}:\,\mu=\mu_{0};\,H_{0}:\,\mu\geq\mu_{0};\,H_{0}:\,\mu\leq\mu_{0}H0:μ=μ0;H0:μ≥μ0;H0:μ≤μ0 。原假设最初被假设是成立的,之后根据样本数据确定是否有足够的证据拒绝原假设。
备则假设:通常是研究者想搜集证据予以支持的假设,记为H1H_{1}H1或HaH_{a}Ha;备则假设表达的含义是指参数有变化、变量之间有联系或总体分布与一理论分布有差异。因此备则假设常写成 H1:μ≠μ0;H1:μ>μ0;H1:μ<μ0H_{1}:\mu\not=\mu_{0};\,H_{1}:\,\mu>\mu_{0};\,H_{1}:\,\mu<\mu_{0}H1:μ=μ0;H1:μ>μ0;H1:μ<μ0。备则假设通常用于表达研究者自己倾向于支持的看法,然后就是想办法收集证据拒绝原假设,支持备则假设。
- 双侧检验:也称双尾检验,指没有特定方向性的备则假设,含有符号≠\not==
- 单侧检验:也称单尾检验,指有特定方向性的备则假设,含有符号>>>(右侧检验)或<<<(左侧检验)
(备则假设就是我们为什么要检验的理由,例如我们检验一个车间生产的零件是否符合标准,我们肯定是认为它不符合标准才需要检验,要是我们认为它标准的话就没必要检验了。因此原假设是符合标准,备择假设是不符合标准)
作出决策
两类错误:
- 第 I 类错误:也称为 α\alphaα 错误,原假设是正确的却拒绝了原假设,概率记为 α\alphaα
- 第 II 类错误:也称为 β\betaβ 错误,原假设是错误的却没有拒绝了原假设,概率记为 β\betaβ
在样本量一定的情况下,α\alphaα 与 β\betaβ 是负相关的;要是 α\alphaα 和 β\betaβ 同时减小只能增大样本量。
显著性水平:即 α\alphaα,通常是人们事先指定的犯第一类错误的概率的最大允许值;一般情况下,人们认为第一类错误的后果更严重,因此会取一个较小的 α\alphaα 值,实际中常用 α=0.01\alpha=0.01α=0.01 ,α=0.05\alpha=0.05α=0.05 和 α=0.1\alpha=0.1α=0.1
① 用统计量决策:首先要根据样本观测结果计算对原假设作出决策的检验统计量。例如要检验总体均值,则可以对样本均值标准化(标准化检验统计量);然后根据实现确定好的显著性水平 α\alphaα 划定拒绝域:
标准化检验统计量=点估计−假设值点估计量的标准差标准化检验统计量=\frac{点估计-假设值}{点估计量的标准差} 标准化检验统计量=点估计量的标准差点估计−假设值
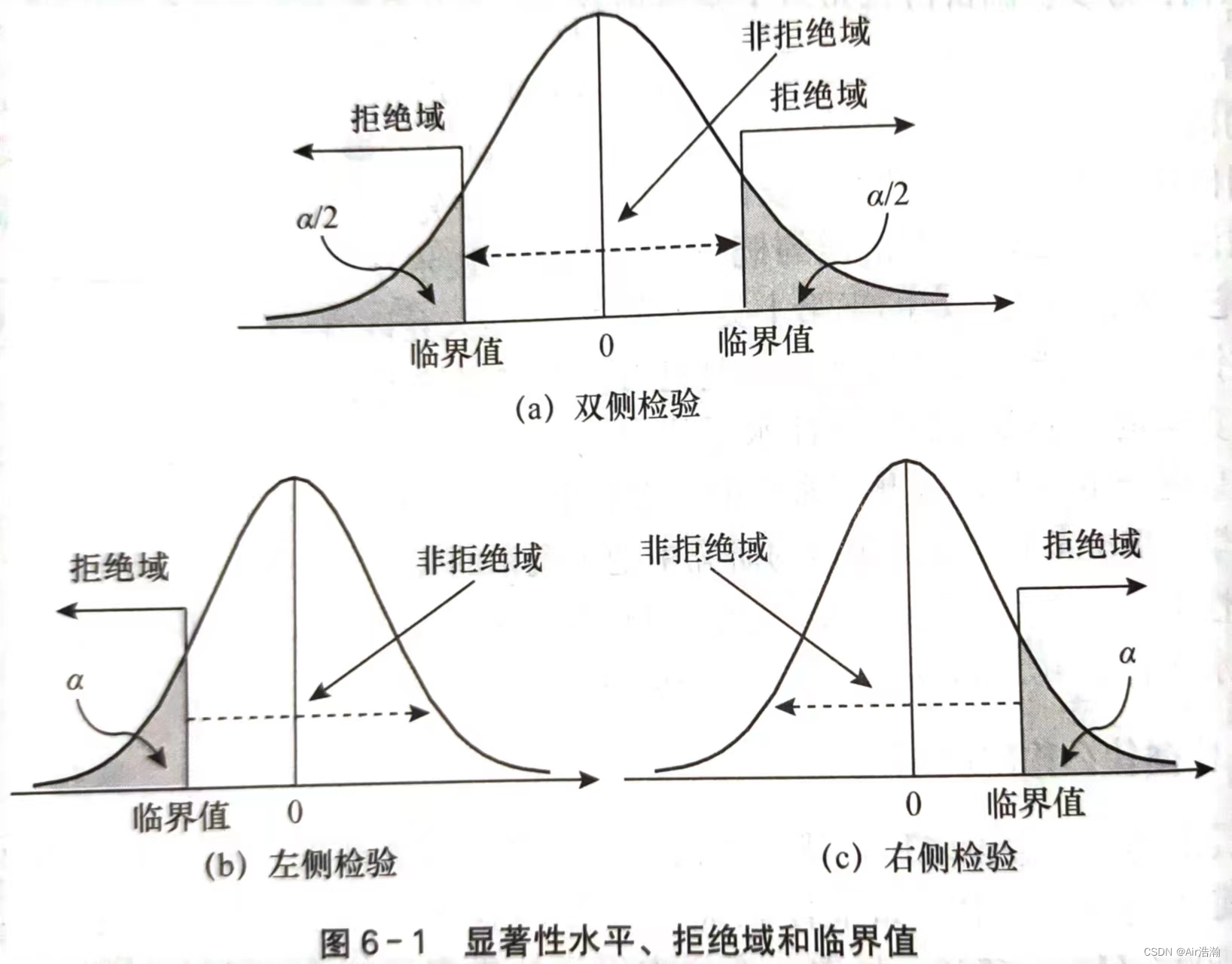
决策准则:
- 双侧检验:|统计量|>临界值,拒绝原假设
- 左侧检验:统计量的值<-临界值,拒绝原假设
- 右侧检验:统计量的值>临界值,拒绝原假设
② 用 PPP 值决策:如果原假设是正确的,所得到的样本结果会像实际观测结果那么极端或者更极端的概率称为 PPP 值 ,也称观察到的显著性水平。
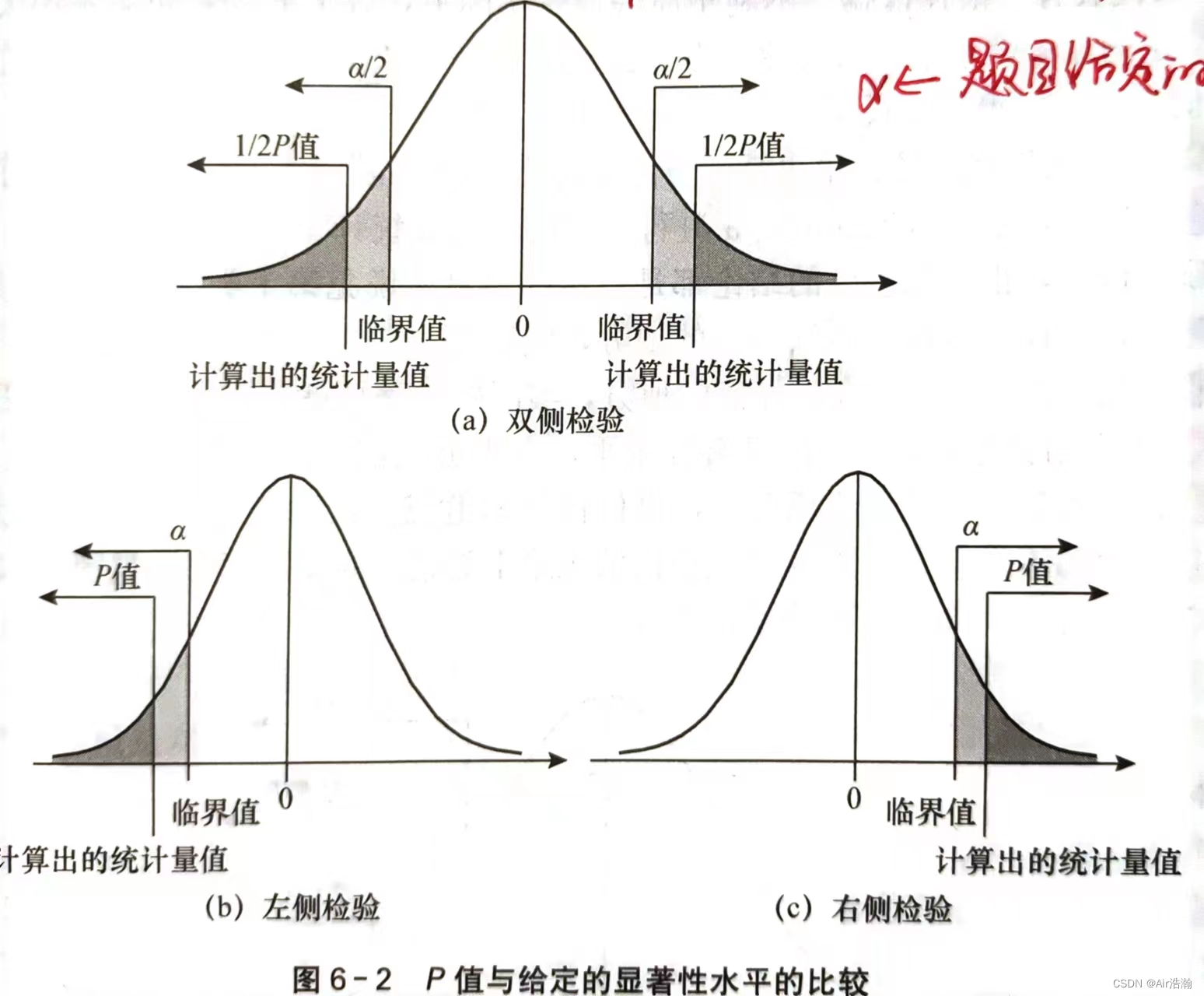
决策准则:
- 如果 P<αP\lt\alphaP<α ,则拒绝 H0H_0H0
- 如果 P>αP>\alphaP>α ,则不拒绝 H0H_0H0
注意:
- PPP 值是关于数据的概率,与原假设对错的概率无关;PPP 值反映的是某个总体的所有样本中某一类数据出现的经常程度。就是说当原假设是正确时,PPP 值就是得到目前这个样本的概率。
(书上解释的跟屎一样;比如我们要检验全小学生月平均生活支出是否为 200020002000 元,H0:μ=2000H_0:\,\mu=2000H0:μ=2000 ,我们统计出来 Xˉ=1750\bar{X}=1750Xˉ=1750 ,P=0.02P=0.02P=0.02,α=0.05\alpha=0.05α=0.05 ,说明如果平均支出真的是 200020002000 的话,那么我们抽到 175017501750 的概率只有 0.020.020.02,太小了,所以可以拒绝原假设)
- PPP 值不一定要和显著性水平 α\alphaα 进行比较,我们可以认为 PPP 值越小,拒绝原假设的理由就越充分,一般要求 PPP 不大于 0.10.10.1
- PPP 值决策优于统计量决策,PPP 值其实是实际上犯 I 类错误的概率。
表述决策结果
- 假设检验不能证明原假设正确,“不拒绝”不代表“接受”,接受 H0H_0H0 的风险由 β\betaβ 衡量;
- 拒绝原假设时,称样本结果在“统计上是显著的”,“显著的”意思是“非偶然的”,但统计上显著不等于有实际意义
一个总体参数的检验
总体均值的检验
大样本的检验:样本均值经标准化后,可认为服从标准正态分布,因而采用正态分布的检验统计量:
- 当总体方差 σ2\sigma^2σ2 已知时,总体均值检验统计量为:
Z=Xˉ−μ0σ/nZ=\frac{\bar{X}-\mu_0}{\sigma/\sqrt{n}} Z=σ/nXˉ−μ0
- 当总体方差 σ2\sigma^2σ2 未知时,可以用样本方差 S2S^2S2 代替,得到总体均值检验统计量为:
Z=Xˉ−μ0S/nZ=\frac{\bar{X}-\mu_0}{S/\sqrt{n}} Z=S/nXˉ−μ0
小样本的检验:
- 当总体方差 σ2\sigma^2σ2 已知时,即使是在小样本的情况下,样本均值经标准化后仍然服从标准正态分布,总体均值检验统计量为:
Z=Xˉ−μ0σ/nZ=\frac{\bar{X}-\mu_0}{\sigma/\sqrt{n}}\ Z=σ/nXˉ−μ0
- 当总体方差未知时,检验统计量满足 t 分布(自由度为 n−1n-1n−1 ),通常称为 t 检验
t=Xˉ−μ0S/nt=\frac{\bar{X}-\mu_0}{S/\sqrt{n}} t=S/nXˉ−μ0
总体比例的检验
大样本的检验:样本比例经过标准化后近似服从标准正态分布,因此总体比例检验统计量为:(π0\pi_0π0 可以是我们猜测的比例)
Z=p−π0π0(1−π0)nZ=\frac{p-\pi_0}{\sqrt{\frac{\pi_0(1-\pi_0)}{n}}} Z=nπ0(1−π0)p−π0
总体方差的检验
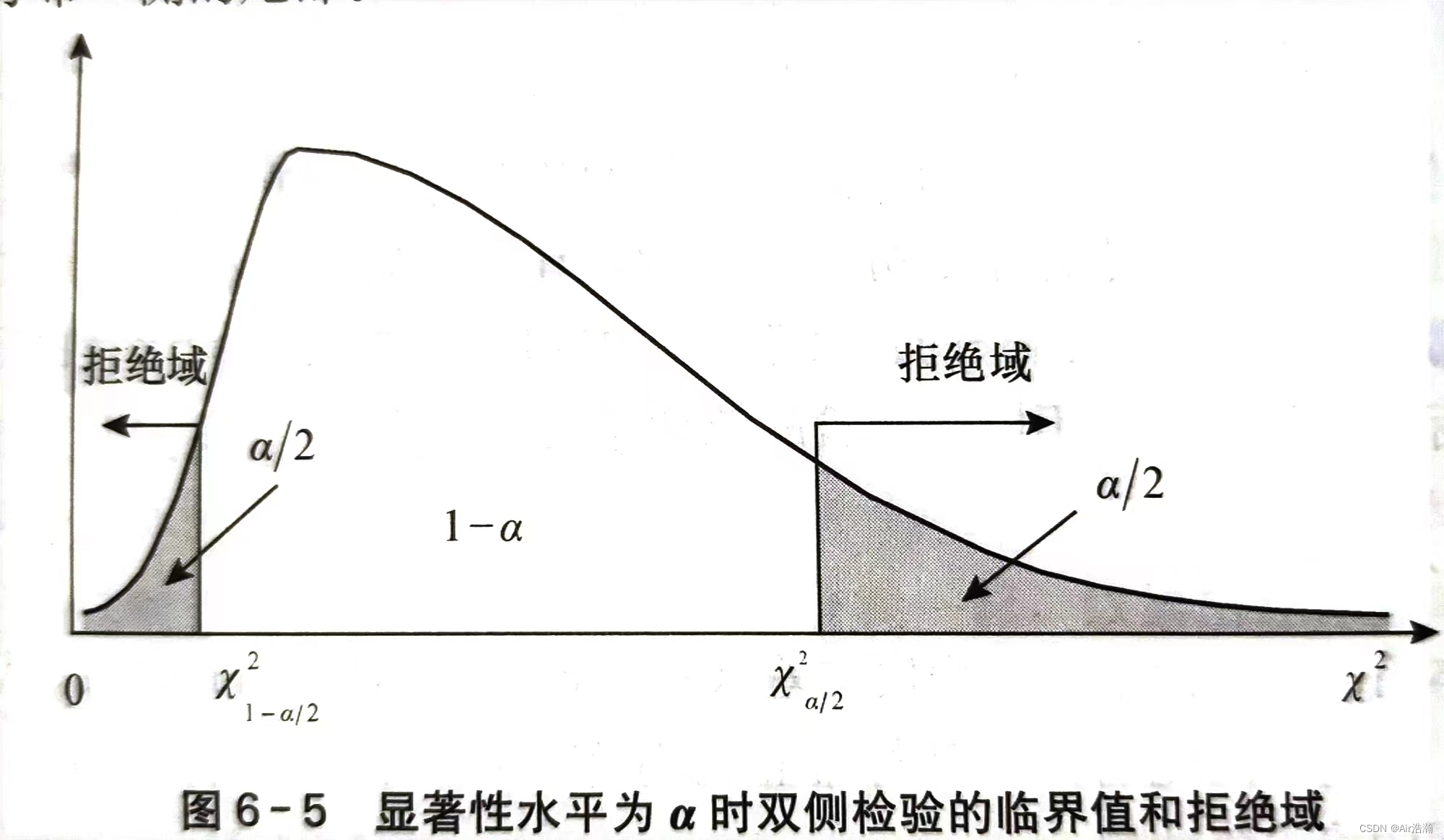
总体方差的检验,不论样本量 nnn 是大是小,都要求总体服从正态分布。总体方差检验统计量为:(σ0\sigma_0σ0 可以是我们猜测的方差)
χ2=(n−1)S2σ02\chi^2=\frac{(n-1)S^2}{\sigma_0^2} χ2=σ02(n−1)S2
(χ2\chi^2χ2 自由度为 n−1n-1n−1 )由于是不对称分布,因此我们采取等尾区间:
两个总体参数的检验
两个总体均值之差的检验
(常用于比如比较两个相似环境下产生的结果是否相同,取 H0:(μ1−μ2)=0H_0:\,(\mu_1-\mu_2)=0H0:(μ1−μ2)=0 )
独立大样本的检验:两样本均值之差经标准化后满足正态分布((μ1−μ2)(\mu_1-\mu_2)(μ1−μ2) 为我们猜测的样本均值之差的值)
- 当总体方差 σ12\sigma_1^2σ12 和 σ22\sigma_2^2σ22 已知时,总体均值检验统计量为:
Z=(X1ˉ−X2ˉ)−(μ1−μ2)σ12n1+σ22n2Z=\frac{(\bar{X_1}-\bar{X_2})-(\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}} Z=n1σ12+n2σ22(X1ˉ−X2ˉ)−(μ1−μ2)
- 当总体方差 σ12\sigma_1^2σ12 和 σ22\sigma_2^2σ22 已知时,分别使用样本方差 S12S_1^2S12 和 S22S_2^2S22 代替,总体均值检验统计量为:
Z=(X1ˉ−X2ˉ)−(μ1−μ2)S12n1+S22n2Z=\frac{(\bar{X_1}-\bar{X_2})-(\mu_1-\mu_2)}{\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}} Z=n1S12+n2S22(X1ˉ−X2ˉ)−(μ1−μ2)
独立小样本的检验:
- 当总体方差 σ12\sigma_1^2σ12 和 σ22\sigma_2^2σ22 已知时,样本均值之差经标准化后仍然服从标准正态分布,总体均值之差检验统计量为:
Z=(X1ˉ−X2ˉ)−(μ1−μ2)σ12n1+σ22n2Z=\frac{(\bar{X_1}-\bar{X_2})-(\mu_1-\mu_2)}{\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}} Z=n1σ12+n2σ22(X1ˉ−X2ˉ)−(μ1−μ2)
- 当总体方差 σ12\sigma_1^2σ12 和 σ22\sigma_2^2σ22 未知,但 σ22=σ22\sigma_2^2=\sigma_2^2σ22=σ22 时,需要将两个样本数据组合在一起,组合后的样本方差 SpS_pSp 为:
Sp=(n1−1)S12+(n2−1)S22n1+n2−2S_p=\frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{n_1+n_2-2} Sp=n1+n2−2(n1−1)S12+(n2−1)S22
样本均值之差标准化后符合自由度为 n1+n2−2n_1+n_2-2n1+n2−2 的 t 分布,检验统计量为:
t=(X1ˉ−X2ˉ)−(μ1−μ2)Sp1n1+1n2t=\frac{(\bar{X_1}-\bar{X_2})-(\mu_1-\mu_2)}{S_p\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}} t=Spn11+n21(X1ˉ−X2ˉ)−(μ1−μ2)
- 当总体方差 σ12\sigma_1^2σ12 和 σ22\sigma_2^2σ22 未知且 σ22≠σ22\sigma_2^2\not=\sigma_2^2σ22=σ22 时,样本均值之差标准化后近似服从自由度为 vvv 的 t 分布,检验统计量为:
t=(X1ˉ−X2ˉ)−(μ1−μ2)S12n1+S22n2t=\frac{(\bar{X_1}-\bar{X_2})-(\mu_1-\mu_2)}{\sqrt{\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2}}} t=n1S12+n2S22(X1ˉ−X2ˉ)−(μ1−μ2)
其中 vvv 为:(需要四舍五入求整数)
v=(S12n1+S22n2)2(S12n1)2n1−1+(S22n2)2n2−1v=\frac{(\frac{S_1^2}{n_1}+\frac{S_2^2}{n_2})^2}{\frac{(\frac{S_1^2}{n_1})^2}{n_1-1}+\frac{(\frac{S_2^2}{n_2})^2}{n_2-1}} v=n1−1(n1S12)2+n2−1(n2S22)2(n1S12+n2S22)2
配对样本的检验:配对样本的检验需要假定两个总体配对差值构成的总体服从正态分布,且配对差是从差值总体中随机抽取的。对于小样本情形,配对差值经标准化后服从自由度为 n−1n-1n−1 的 t 分布,因此选择的检验统计量为:
t=dˉ−(μ1−μ2)Sd/nt=\frac{\bar{d}-(\mu_1-\mu_2)}{S_d/\sqrt{n}} t=Sd/ndˉ−(μ1−μ2)
其中 dˉ\bar{d}dˉ 为配对差值的平均数,SdS_dSd 为配对差值的标准差
两个总体比例之差的检验
独立大样本:要求两个样本都是大样本,即 n1p1n_1p_1n1p1 ,n1(1−p1)n_1(1-p_1)n1(1−p1) ,n2p2n_2p_2n2p2 和 n2(1−p2)n_2(1-p_2)n2(1−p2) 都大于等于 101010 。根据两个样本比例之差的标准化的抽样分布,可以得到总体比例之差检验统计量为:
Z=(p1−p2)−(π1−π2)σp1−p2Z=\frac{(p_1-p_2)-(\pi_1-\pi_2)}{\sigma_{p_1-p_2}} Z=σp1−p2(p1−p2)−(π1−π2)
其中 σp1−p2=π1(1−π1)n1+π2(1−π2)n2\sigma_{p_1-p_2}=\sqrt{\frac{\pi_1(1-\pi_1)}{n_1}+\frac{\pi_2(1-\pi_2)}{n_2}}σp1−p2=n1π1(1−π1)+n2π2(1−π2) 是两个样本比例之差抽样分布的标准差。但是你发现 π1\pi_1π1 和 π2\pi_2π2 事先都是不知道的,分为两种情况:
- 检验两个总体比例是否相等,即 H0:π1−π2=0H_0:\,\pi_1-\pi_2=0H0:π1−π2=0 ,H1:π2−π2≠0H_1:\,\pi_2-\pi_2\not=0H1:π2−π2=0 ;此时 π1\pi_1π1 和 π2\pi_2π2 的最佳估计是将两个样本合并后得到的比例,为:
p=p1n1+p2n2n1+n2p=\frac{p_1n_1+p_2n_2}{n_1+n_2} p=n1+n2p1n1+p2n2
此时 σπ1−π2\sigma_{\pi_1-\pi_2}σπ1−π2 的最佳估计量为:
σπ1−π2=p(1−p)(1n1+1n2)\sigma_{\pi_1-\pi_2}=\sqrt{p(1-p)(\frac{1}{n_1}+\frac{1}{n_2})} σπ1−π2=p(1−p)(n11+n21)
代入得到两个总体比例之差的检验统计量为:
Z=p1−p2p(1−p)(1n1+1n2)Z=\frac{p_1-p_2}{\sqrt{p(1-p)(\frac{1}{n_1}+\frac{1}{n_2})}} Z=p(1−p)(n11+n21)p1−p2
- 检验两个总体比例之差是否是个常数,即 H0:π1−π2=d0H_0:\,\pi_1-\pi_2=d_0H0:π1−π2=d0 ,H1:π2−π2≠d0H_1:\,\pi_2-\pi_2\not=d_0H1:π2−π2=d0 ,这时可直接用两个样本的比例 p1p_1p1 和 p2p_2p2 作为两个总体比例 π1\pi_1π1 和 π2\pi_2π2 的估计,从而得到两个总体比例之差的检验统计量为:
Z=(p1−p2)−d0p1(1−p1)n1+p2(1−p2)n2Z=\frac{(p_1-p_2)-d_0}{\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}} Z=n1p1(1−p1)+n2p2(1−p2)(p1−p2)−d0
(也有可能是这样:H0:π1−π2≥0H_0:\,\pi_1-\pi_2\ge 0H0:π1−π2≥0 ,H1:π1−π2<0H_1:\,\pi_1-\pi_2<0H1:π1−π2<0 或者 H0:π1−π2≤0H_0:\,\pi_1-\pi_2\le 0H0:π1−π2≤0 ,H1:π1−π2>0H_1:\,\pi_1-\pi_2>0H1:π1−π2>0 ,都当作第一种来处理,要注意等号总是在原假设里)
两个总体方差比的检验
对总体方差比的假设通常是跟 111 相比,就是看两个总体谁的方差更大一些。由于两个样本方差之比 S12S22\frac{S_1^2}{S_2^2}S22S12 是两个总体方差之比 σ12σ22\frac{\sigma_1^2}{\sigma_2^2}σ22σ12 的理想估计量,故检验统计量为:(符合 F(n1,n2)F(n_1,\,n_2)F(n1,n2) 分布)
F=S12S22F=\frac{S_1^2}{S_2^2} F=S22S12
双侧检验通常是用较大的样本方差除以较小的样本方差,这样拒绝域总是发生在 F 分布的右侧。在左侧检验时,也可以安排为右侧检验。
总体分布的检验
总体正态性检验:根据样本数据检验总体上是否服从正态分布,检验方法有图示法和检验法。
正态性检验的图示法
正态概率图:有两种:
- Q−QQ-QQ−Q 图:根据观测值的实际分位数与理论分布(如正态分布)的分位数绘制的
- P−PP-PP−P 图:根据观测数据的累积概率与理论分布(如正态分布)的符合程度绘制的
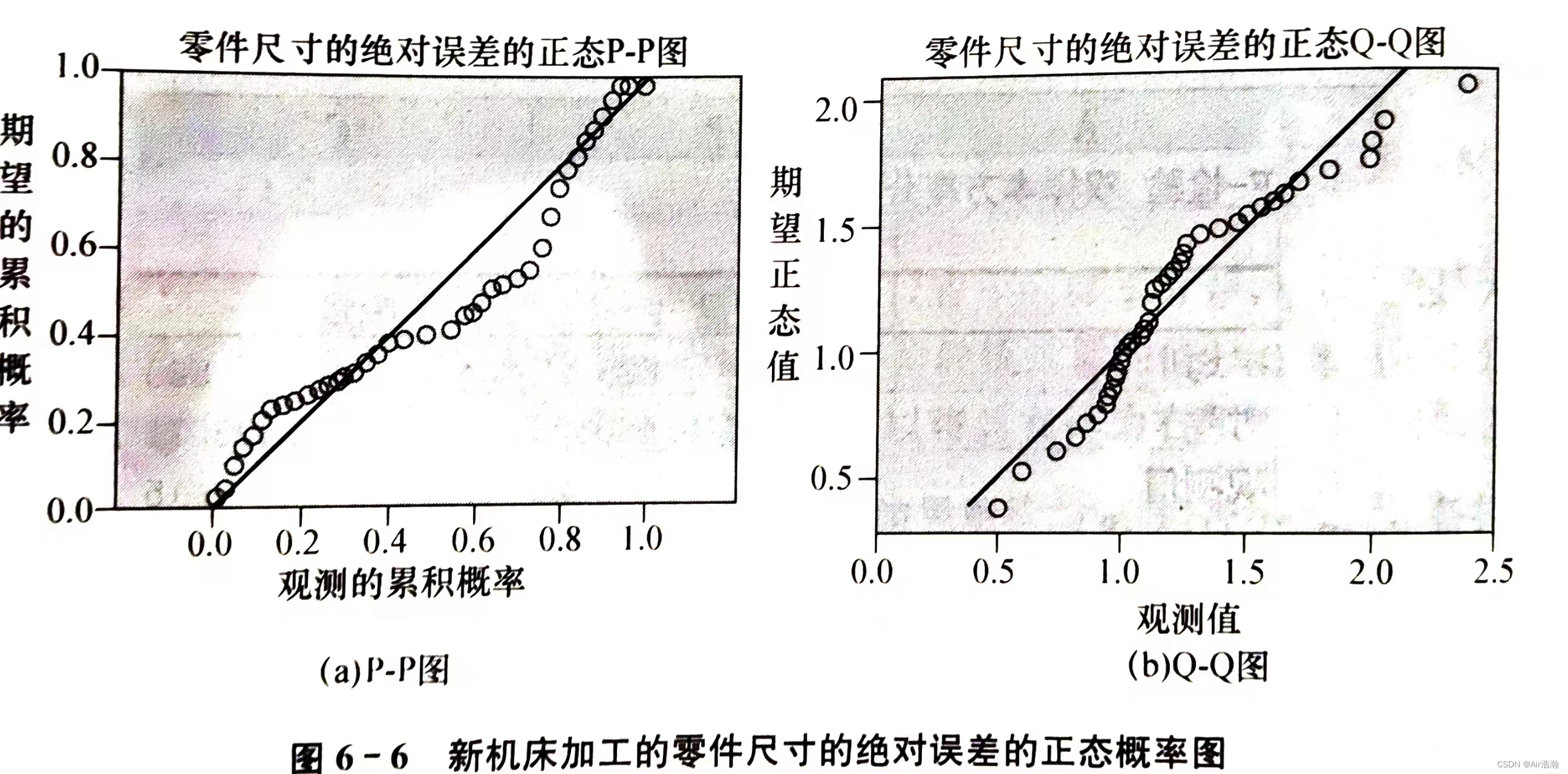
-
图中直线表示理论正态分布线,各观测点越靠近直线,且呈随机分布,表明数据越接近正态分布。
-
实际使用时并不一定要参考理论正态分布线,只要所有点都在一条直线的周围随机分布即可
-
由于正态概率图中的点很少,提供的正态性信息有限,适用于大样本量;
Shapiro-Wilk 和 K-S 正态性检验
当样本量较小时,可以使用标准的统计检验办法,即假设总体服从正态分布,如果检验获得的 PPP 值小于显著性水平 α\alphaα ,则拒绝原假设。
Shapiro-Wilk 方法:(适用于小样本)H0H_0H0 :总体服从正态分布,H1H_1H1 :总体不服从正态分布,然后计算检验统计量 WWW :
W=∑aiyi2∑(yi−yˉ)2W=\frac{\sum a_iy_i^2}{\sum(y_i-\bar{y})^2} W=∑(yi−yˉ)2∑aiyi2
- yiy_iyi 为排序后的样本数据,yˉ\bar{y}yˉ 是样本均值
- aia_iai 时样本量为 nnn 所对应的系数,通过:
[a1,⋯,an]=mTV−1∣∣V−1m∣∣\begin{bmatrix}a_1,\cdots,a_n\end{bmatrix}=\frac{m^{T}V^{-1}}{||V^{-1}m||} [a1,⋯,an]=∣∣V−1m∣∣mTV−1
- VVV 是这些有序统计量的协方差
- m=[m1,⋯,mn]m=\begin{bmatrix}m_1,\cdots,m_n\end{bmatrix}m=[m1,⋯,mn] ,其中 mim_imi 是从一个标准的正态分布随机变量上采样的有序独立同分布的统计量的期望值
WWW 的最大值是 111 ,最小值是 na12n=1\frac{na_1^2}{n=1}n=1na12 ,统计量越大表示越符合正态分布。当然,非正态分布的小样本数据也有可能有较大的 WWW 值,而且由于该统计量的分布是未知的,因此需要通过模拟或者查表来估计概率。
Kolmogorov-Smirnov 检验:既适合大样本,又适合小样本,而且不止可以检验正态分布。将实际频数和期望频数进行比较,检验其拟合程度。具体来说,是将某一变量的积累分布函数与特定的分布函数进行比较。设总体的积累分布函数为 F(x)F(x)F(x) ,已知理论分布函数为 F0(x)F_0(x)F0(x) ,则:
H0:F(x)=F0(x);H1:F(x)≠F0(x);H_0:\,F(x)=F_0(x);\quad H_1:\,F(x)\not=F_0(x); H0:F(x)=F0(x);H1:F(x)=F0(x);
各样本观察值的实际累计概率为 S(x)S(x)S(x) ,实际累计概率与理论累计概率的差值为 D(x)D(x)D(x) ,差值序列中最大的绝对差值:
D=max(∣S(xi)−F(xi)∣)D=max(|S(x_i)-F(x_i)|) D=max(∣S(xi)−F(xi)∣)
实际累计概率肯定是离散值,因此可以修正为:
D=max((∣S(xi)−F(xi)∣),(∣S(xi−1)−F(xi)∣))D=max((|S(x_i)-F(x_i)|),\,(|S(x_{i-1})-F(x_i)|)) D=max((∣S(xi)−F(xi)∣),(∣S(xi−1)−F(xi)∣))
在小样本情况下,统计量 DDD 服从 Kolmogorov 分布;在大样本情况下,则用正态分布近似,统计量为:
Z=nDZ=\sqrt{n}D Z=nD
如果原假设成立,则每次抽样得到的 DDD 值应当不会偏离 000 太远。
K-S要求样本数据是连续的数值型数据,且要求理论分布已知。总体均值和方差未知时也可以用 Xˉ\bar{X}Xˉ 和 S2S^2S2 代替。
总结
相关文章:

统计学 假设检验
文章目录假设检验假设检验的基本原理提出假设作出决策表述决策结果一个总体参数的检验总体均值的检验总体比例的检验总体方差的检验两个总体参数的检验两个总体均值之差的检验两个总体比例之差的检验两个总体方差比的检验总体分布的检验正态性检验的图示法Shapiro-Wilk 和 K-S …...
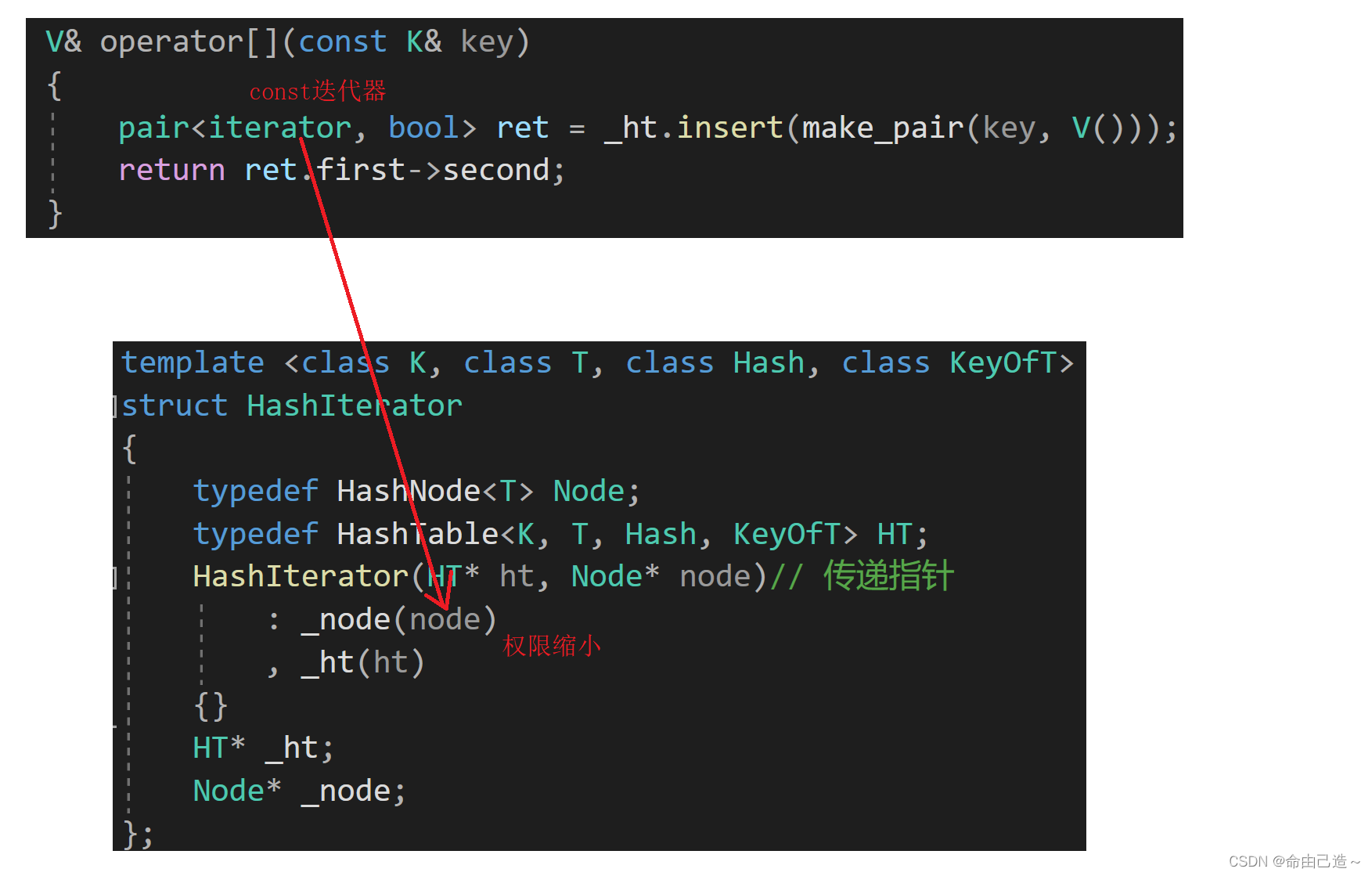
【C++】哈希
哈希一、unordered系列关联式容器二、哈希原理2.1 哈希映射2.2 哈希冲突2.2.1 闭散列—开放地址法2.2.2 代码实现2.2.3 开散列—拉链法2.2.4 代码实现三、哈希封装unordered_map/unordered_set3.1 基本框架3.2 迭代器实现3.2.3 operator*和operator->和operator!3.2.4 opera…...
「TCG 规范解读」PC 平台相关规范(3)
可信计算组织(Ttrusted Computing Group,TCG)是一个非盈利的工业标准组织,它的宗旨是加强在相异计算机平台上的计算环境的安全性。TCG于2003年春成立,并采纳了由可信计算平台联盟(the Trusted Computing Platform Alli…...
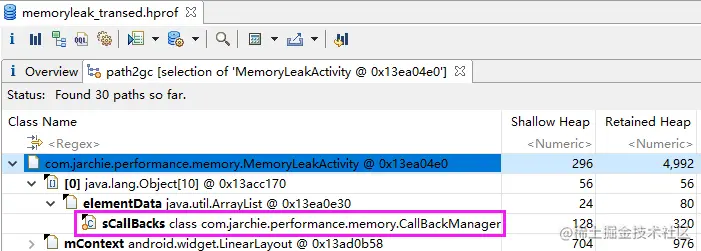
这篇教你搞定Android内存优化分析总结
一、内存优化概念1.1 为什么要做内存优化?内存优化一直是一个很重要但却缺乏关注的点,内存作为程序运行最重要的资源之一,需要运行过程中做到合理的资源分配与回收,不合理的内存占用轻则使得用户应用程序运行卡顿、ANR、黑屏&…...

概率论与数理统计期末小题狂练 11-12两套,12-13-1
11-12第一学期A1 略。2 X服从正态分布N(0,1),X^2服从卡方分布。又考查了卡方分布均值和方差公式。一开始如果对本题无从下手,大概是没看出来是什么分布。3 第二小空本身也可以作为一个结论。4 考查切比雪夫不等式&…...

golang对字符串的处理操作 如何正确理解 rune byte和string
fmt.Printf相关参数介绍 先来看代码的演示 package mainimport ("fmt""unicode/utf8" )func main() {s:"我爱中国人haha!"fmt.Println(len(s))//20个字节 一个中文三个字节 1541fmt.Print("\n echo byte \n")for k,v: range []byte(…...
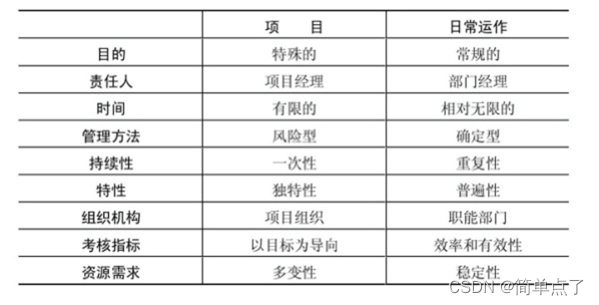
软件项目管理简答题复习(1)
1.项目:创造唯一的产品,唯一的服务临时性的努力 2.项目特征:不可见性,复杂性,一致性,变更性,特殊性 3.项目和日常活动的区别? 项目具有特殊性,负责人是项目经理&#…...
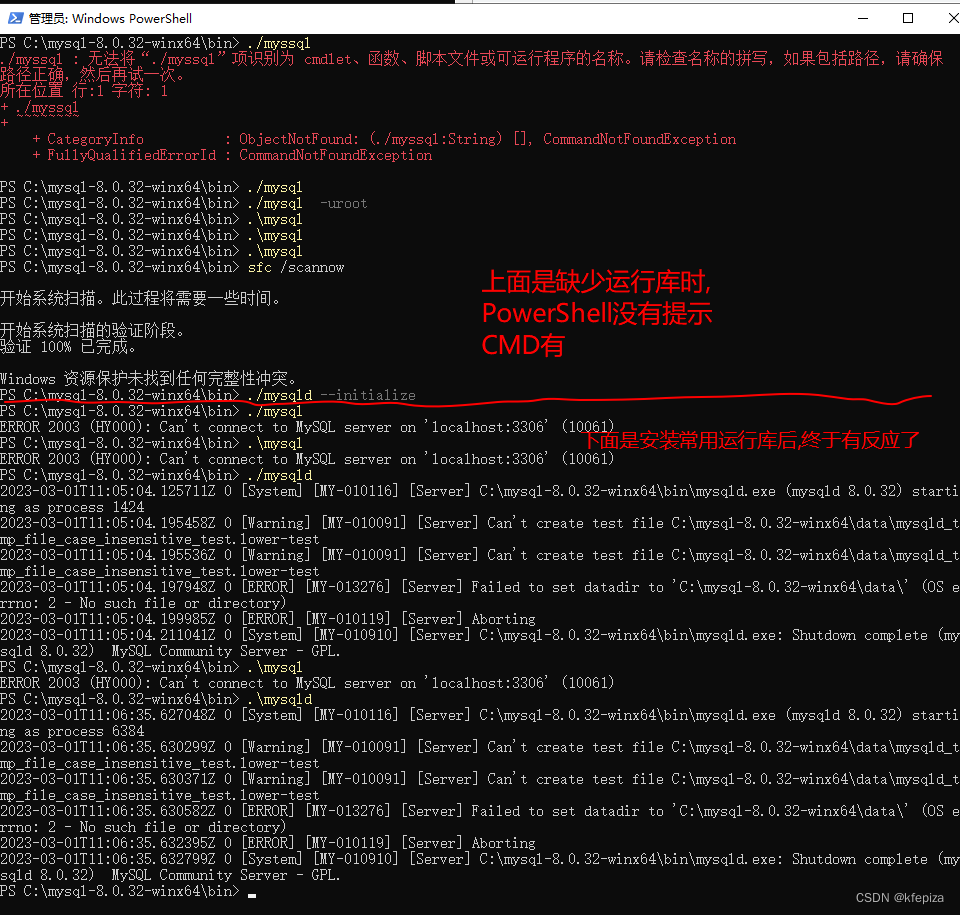
云Windows Server 2022 Datacenter 安装MySQL8解压缩版 mysql-8.0.32-winx64 230301记录
MySQL Community Downloads MySQL社区版压缩包下载地址 https://dev.mysql.com/downloads/mysql/ 解压到了C盘 没打算设置环境变量 右键点击开始 或 winx 以管理员身份打开 PowerShell 进入到安装目录下的 bin 目录 可以输入cd 后, 拖动 bin 文件夹到控制台&…...

如何使用BeaconEye监控CobaltStrike的Beacon
关于BeaconEye BeaconEye是一款针对CobaltStrike的安全工具,该工具可以扫描正在运行的主动CobaltStrike Beacon。当BeaconEye扫描到了正在运行Beacon的进程之后,BeaconEye将会监控每一个进程以查看C2活动。 工作机制 BeaconEye将会扫描活动进程或Mini…...
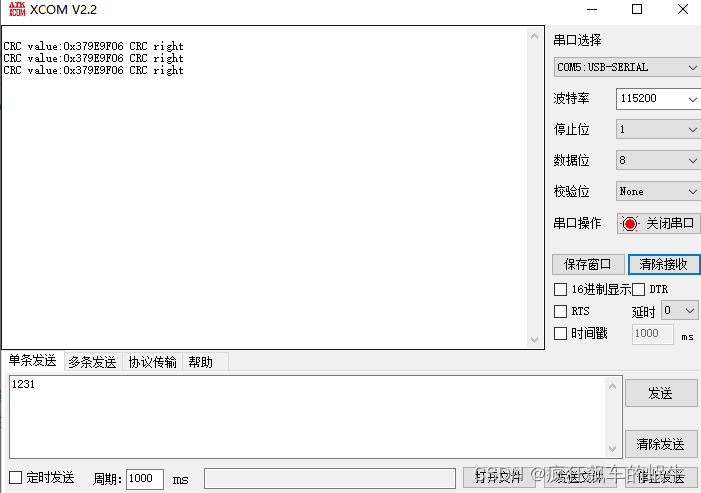
STM32开发(17)----CubeMX配置CRC
CubeMX配置CRC前言一、什么是CRC?二、实验过程1.STM32CubeMX配置2.代码实现重载printf3.实验结果总结前言 本章介绍使用STM32CubeMX对CRC进行配置的方法,CRC的目的是保证数据的完整性,所有的STM32芯片都内置了一个硬件的CRC计算模块…...
【MySQL】基础操作:登录、访问、退出和卸载
一、MySQL简介 MySQL数据库最初是由瑞典MySQL AB公司开发,2008年1月16号被Sun公司收购。2009年,SUN又被Oracle收购。MySQL是目前IT行业最流行的开放源代码的数据库管理系统,同时它也是一个支持多线程、高并发、多用户的关系型数据库管理系统。…...
)
【算法经典题集】递推(持续更新~~~)
😽PREFACE🎁欢迎各位→点赞👍 收藏⭐ 评论📝📢系列专栏:算法经典题集🔊本专栏涉及到的知识点或者题目是算法专栏的补充与应用💪种一棵树最好是十年前其次是现在递推简单的斐波那契…...

mysql兼容性验证
MySQL是一个关系型数据库管理系统。 一、安装启动 安装mysql相关软件包 yum install mysql-server 启动mysql服务 systemctl start mysqld systemctl status mysqld mysql数据库启动失败问题汇总: <问题1>、start mysqld显示失败,如下所示&…...

C++回顾(五)—— 构造函数和析构函数
5.1 构造和析构 5.1.1 构造函数 (1)定义 1)C中的类可以定义与类名相同的特殊成员函数,这种与类名相同的成员函数叫做构造函数;2)构造函数在定义时可以有参数;3)没有任何返回类型的…...

嵌入式学习笔记——概述
嵌入式系统概述前言“嵌入式系统”概念1.是个啥?2.可以干啥?3.有哪些入坑方向?4.入坑后可以有多少薪资?单片机1.什么是单片机?2.架构简介3.基于ARM架构的单片机结构简介总结前言 断更很长时间了,写博客确实…...
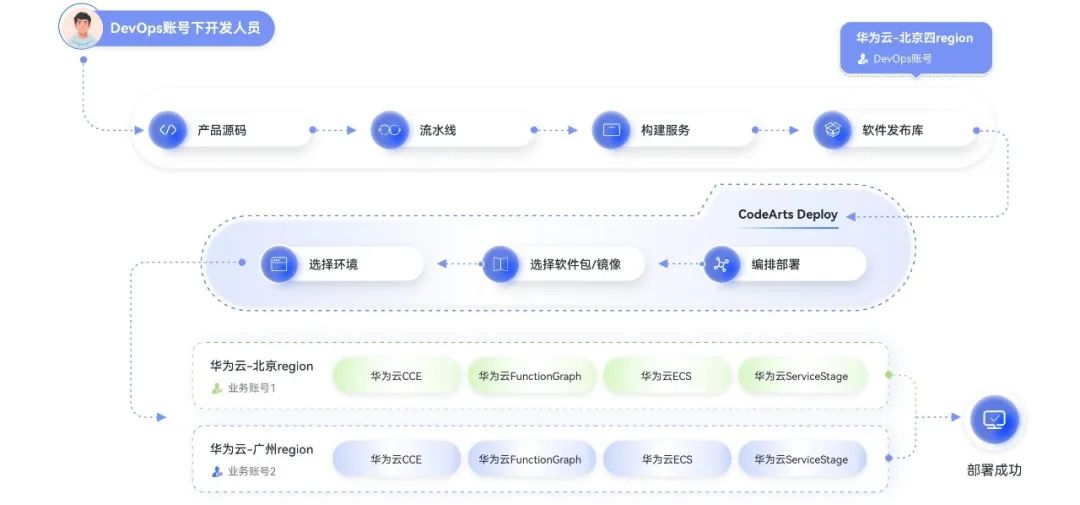
化繁为简高效部署 华为云发布部署服务CodeArts Deploy
随着互联网、数字化的发展,公司机构与各类企业往往需要进行大量频繁的软件部署,部署设备类型多样,如:本地机器、云上裸金属服务器、云上虚拟机与容器等。面对多种部署模式、分布式复杂运行环境,如何用最短时间、高质…...

注意力机制详解系列(四):混合注意力机制
👨💻作者简介: 大数据专业硕士在读,CSDN人工智能领域博客专家,阿里云专家博主,专注大数据与人工智能知识分享。 🎉专栏推荐: 目前在写CV方向专栏,更新不限于目标检测、OCR、图像分类、图像分割等方向,目前活动仅19.9,虽然付费但会长期更新,感兴趣的小伙伴可以…...

Makefiles学习1
初识"Makefiles" 创建一个 “Makefile” 文件 touch Makefile“touch” 用于修改文件或者目录的时间属性,包括访问时间和修改时间,若文件不存在,则重新建立一个新的文件。这里有两个需要我们注意的: 进入并编辑"…...
日志框架以及如何使用LogBack记录程序
使用日志框架可以记录一个程序运行的过程和详情,同时便捷地存储到文件里面,并且性能和灵活性都比较好。日志的体系结构包括两类日志规范接口:Commons Logging,简称:JCL;Simple Logging Facade for Java&…...
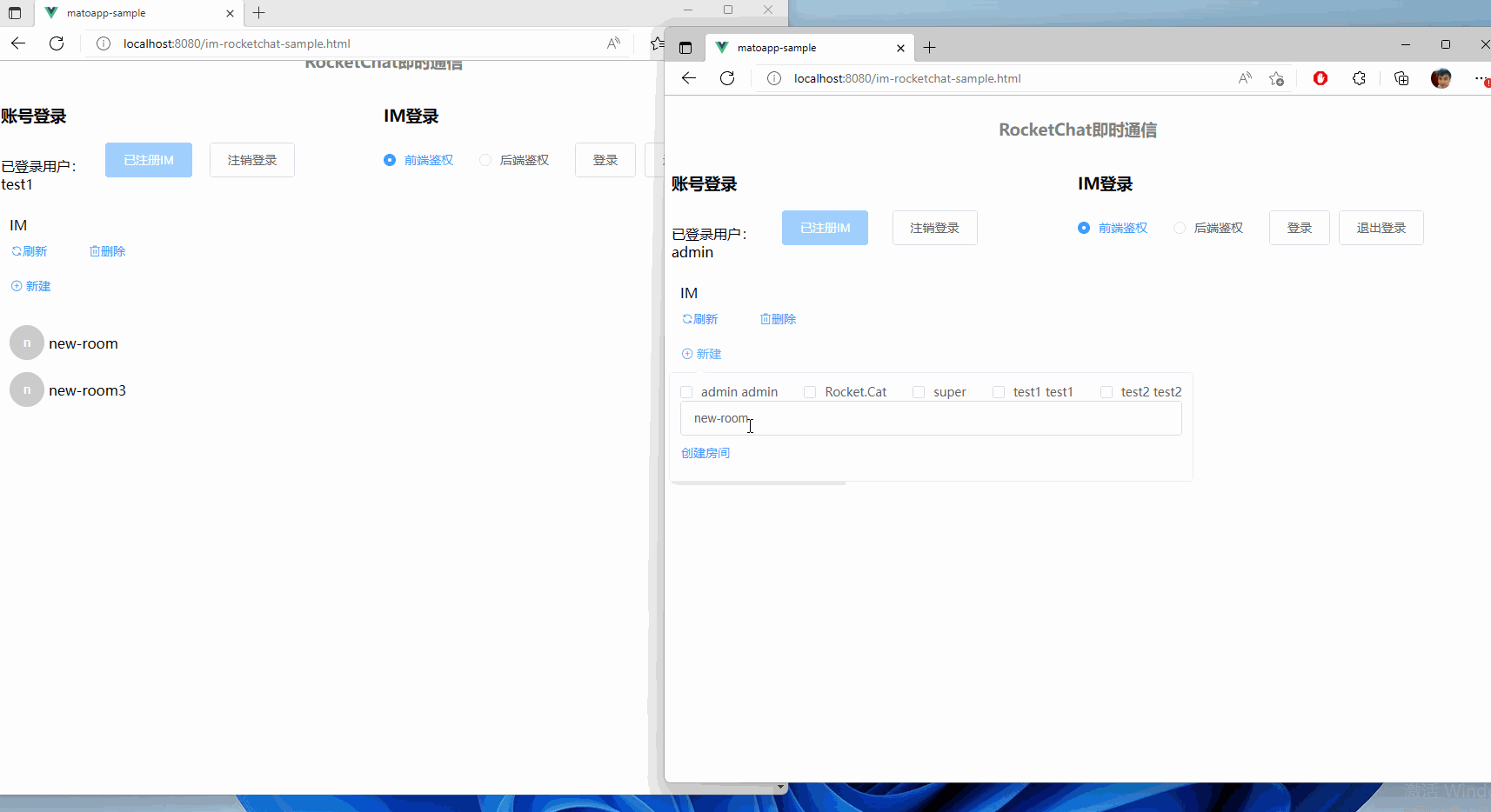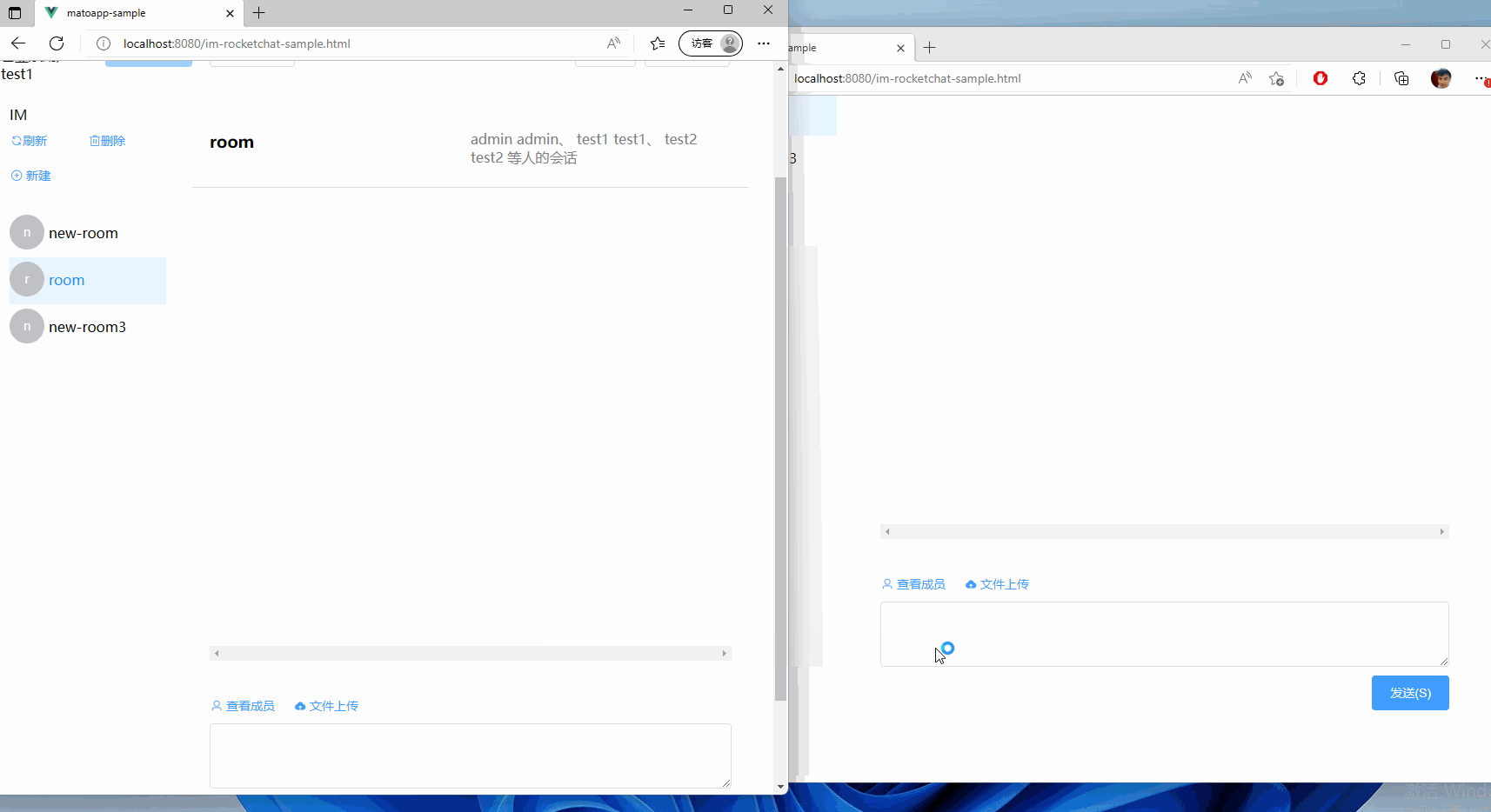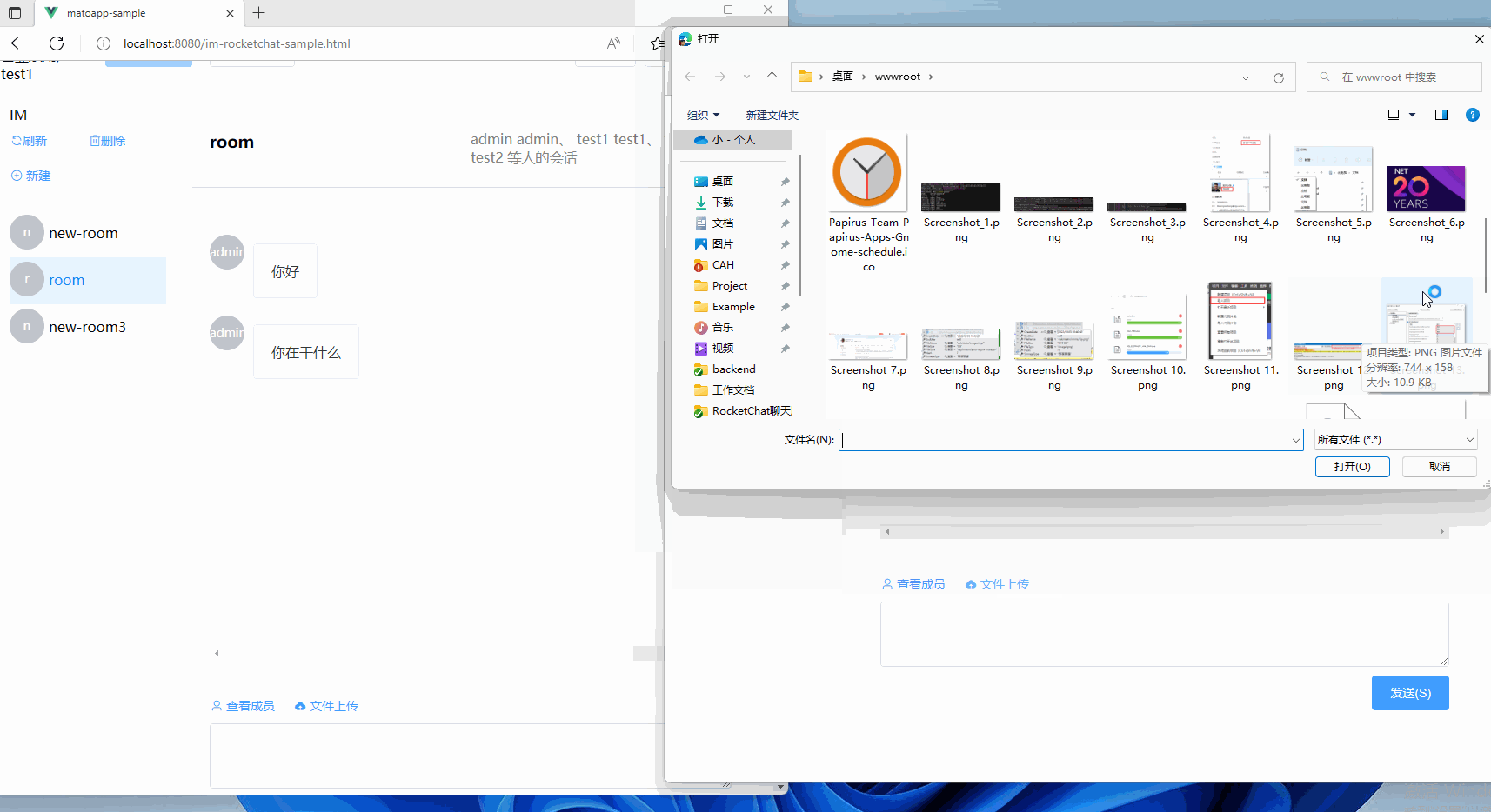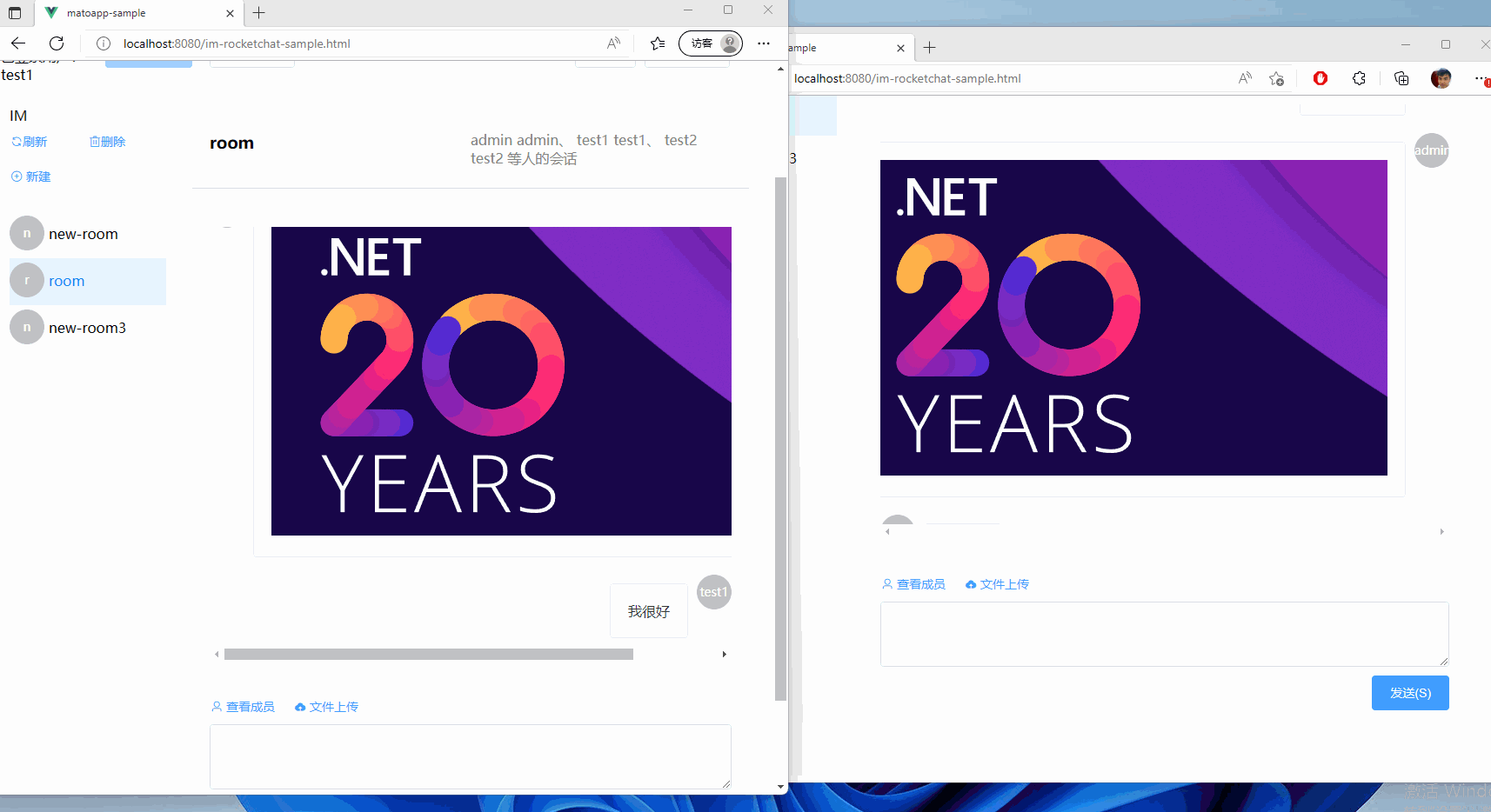
集成RocketChat至现有的.Net项目中,为ChatGPT铺路
文章目录前言项目搭建后端前端代理账号鉴权方式介绍登录校验模块前端鉴权方式后端鉴权方式登录委托使用登录委托处理聊天消息前端鉴权方式后端校验方式项目地址前言 今天我们来聊一聊一个Paas的方案,如何集成到一个既有的项目中。 以其中一个需求为例子:…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
