最小生成树(Minimum Spanning Tree)及生成MST的几种方法
最小生成树 (Minimum Spanning Tree)
最小生成树是图论领域的一个基本概念,适用于加权连通图,其中包括若干顶点(节点)以及连接这些顶点的边(边可以有权重)。在一个加权连通图中,生成树(Spanning Tree)是一个无环子图,它包含图中的所有顶点,并且用最少数量的边将它们连接起来。注意,无环是指子图中不存在任何边的闭环,最少数量的边意味着任意两个顶点之间有且仅有一条路径相互到达。
“最小生成树”这一术语的“最小”指的是在所有可能的生成树中,边的权重之和最小的那一个。在实际应用中,最小生成树可以帮助找到在网络设计、电路设计等方面成本最低的方案。
我们来举一个简单的例子。假设有四个城市,每两个城市之间可以修建道路相连,不同的道路成本不同,现在的目标是花最少的成本将这四个城市全部连通。最小生成树算法即是解决此类问题的有效工具。
生成最小生成树的算法
接下来,我们将介绍四个生成最小生成树的经典算法,它们分别是克鲁斯卡尔(Kruskal)算法和普里姆(Prim)算法,以及相对少见的Borůvka算法和Sollin算法。
1. 克鲁斯卡尔(Kruskal)算法
克鲁斯卡尔算法是基于边的贪心策略。它的基本思想是按照边权重从小到大的顺序选择边,从而构造最小生成树。选取的边必须满足添加后不形成环路。
伪代码:
KRUSKAL(G):A = ∅ // A将存储最小生成树的边对于G中的每个顶点v:MAKE-SET(v)将G中的所有边按权重由低到高排序对于每条边(u, v)按序做如下操作:if FIND-SET(u) ≠ FIND-SET(v): // 检查u和v是否在树的不同分量中A = A ∪ {(u, v)} // 将边(u, v)加入到A中UNION(u, v) // 将u和v的分量合并返回A
其中 MAKE-SET、FIND-SET 和 UNION 是不相交集合数据结构的操作,用于维护和查询顶点间是否存在环路。
2. 普里姆(Prim)算法
普里姆算法是基于点的贪心策略。在这个算法中,我们从任选的一个顶点开始构建最小生成树,逐步扩大树的范围,每一步都添加一条连接树与非树顶点且权重最小的边。
伪代码:
PRIM(G, w, r): // G是图,w是权重函数,r是开始顶点for each u ∈ G.V:u.key = ∞ // 初始化所有顶点的键值为无穷大u.π = NIL // π属性用来记录最小生成树的父节点r.key = 0Q = G.Vwhile Q ≠ ∅:u = EXTRACT-MIN(Q) // 从Q中取出键值最小的顶点ufor each v ∈ G.Adj[u]: // 遍历u的所有邻居vif v ∈ Q and w(u, v) < v.key:v.π = u // 更新v的父节点为uv.key = w(u, v) // 更新v的键值为u与v之间边的权重
在Prim算法中,EXTRACT-MIN(Q)是优先队列的操作,它用于选择权重最小的边,而G.Adj[u]表示图中与顶点u相邻的所有顶点集合。
3. Borůvka算法
Borůvka算法是最早的最小生成树算法之一,适用于稀疏图。算法的每个阶段为图中的每个连通分量选择一条权重最小的边,并将这些边添加到生成树中,直到图变为连通的。
伪代码:
BORUVKA(G):forest = each vertex in G is a separate treewhile there is more than one tree in the forest:for each tree T in the forest:find the smallest edge connecting T to another treeadd this edge to the forestreturn the edges added to the forest
4. Sollin算法
Sollin算法(也被称为Borůvka的改进版本)同样适用于稀疏图,其基本想法是在每个阶段找到每个连通分量键值最小的边,并将它们加入生成树,像Borůvka算法一样重复这个过程,直到所有分量合并到一起。
伪代码:
SOLLIN(G):Initialize a forest F with each vertex in G as a separate treewhile F has more than one tree dofor each tree T in the forest F dolet e = the lightest edge with one end in Tif there is no edge chosen for T or e is lighter than the already chosen edgechoose e for Tfor each edge e chosen in this round doif e connects two different trees thenadd e to the forest Freturn the forest F as the minimum spanning tree
在Sollin算法中,检查加入边e后是否会造成环路的操作通过查询树的根节点来实现,保证了每次迭代加入的边一定属于不同的连通分量。
如果你想更深入地了解人工智能的其他方面,比如机器学习、深度学习、自然语言处理等等,也可以点击这个链接,我按照如下图所示的学习路线为大家整理了100多G的学习资源,基本涵盖了人工智能学习的所有内容,包括了目前人工智能领域最新顶会论文合集和丰富详细的项目实战资料,可以帮助你入门和进阶。
链接: 人工智能交流群(大量资料)

相关文章:

最小生成树(Minimum Spanning Tree)及生成MST的几种方法
最小生成树 (Minimum Spanning Tree) 最小生成树是图论领域的一个基本概念,适用于加权连通图,其中包括若干顶点(节点)以及连接这些顶点的边(边可以有权重)。在一个加权连通图中,生成树…...
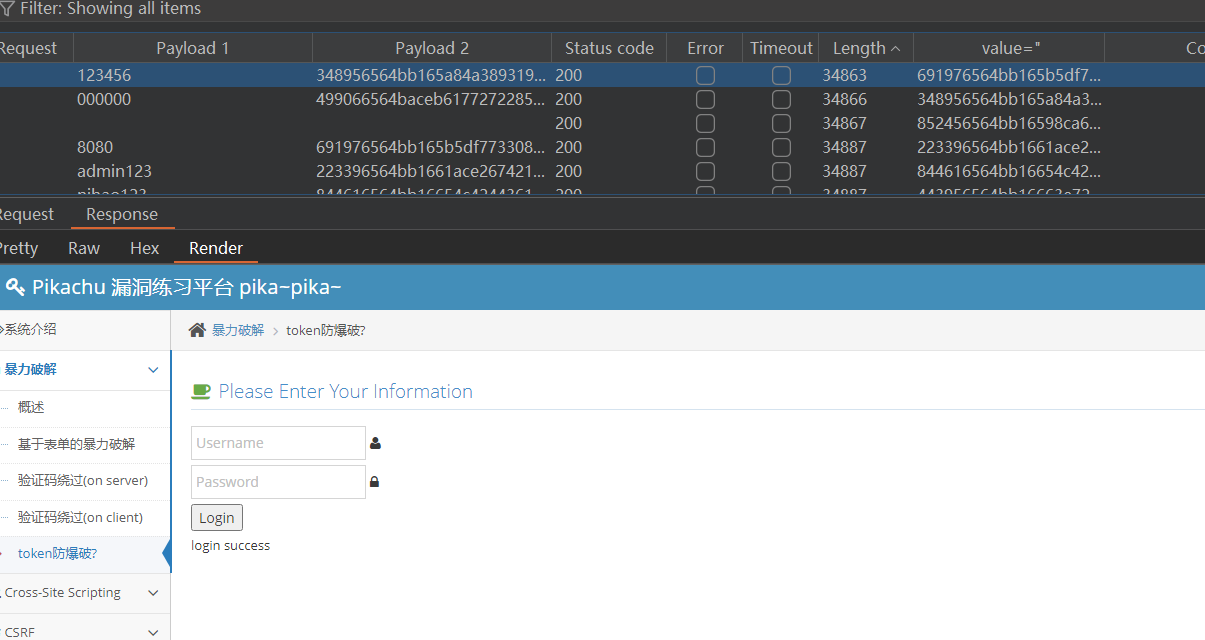
逻辑漏洞 暴力破解(DVWA靶场)与验证码安全 (pikachu靶场) 全网最详解包含代码审计
逻辑漏洞 暴力破解(DVWA靶场)与验证码安全 (pikachu靶场) 全网最详解包含代码审计 0x01 前言 在当今互联网的广袤世界中,各式交互平台层出不穷。每一个交互平台几乎都要求用户注册账号,而这些账号则成为我们在数字世界中的身份象征。账号的安全性变得至…...
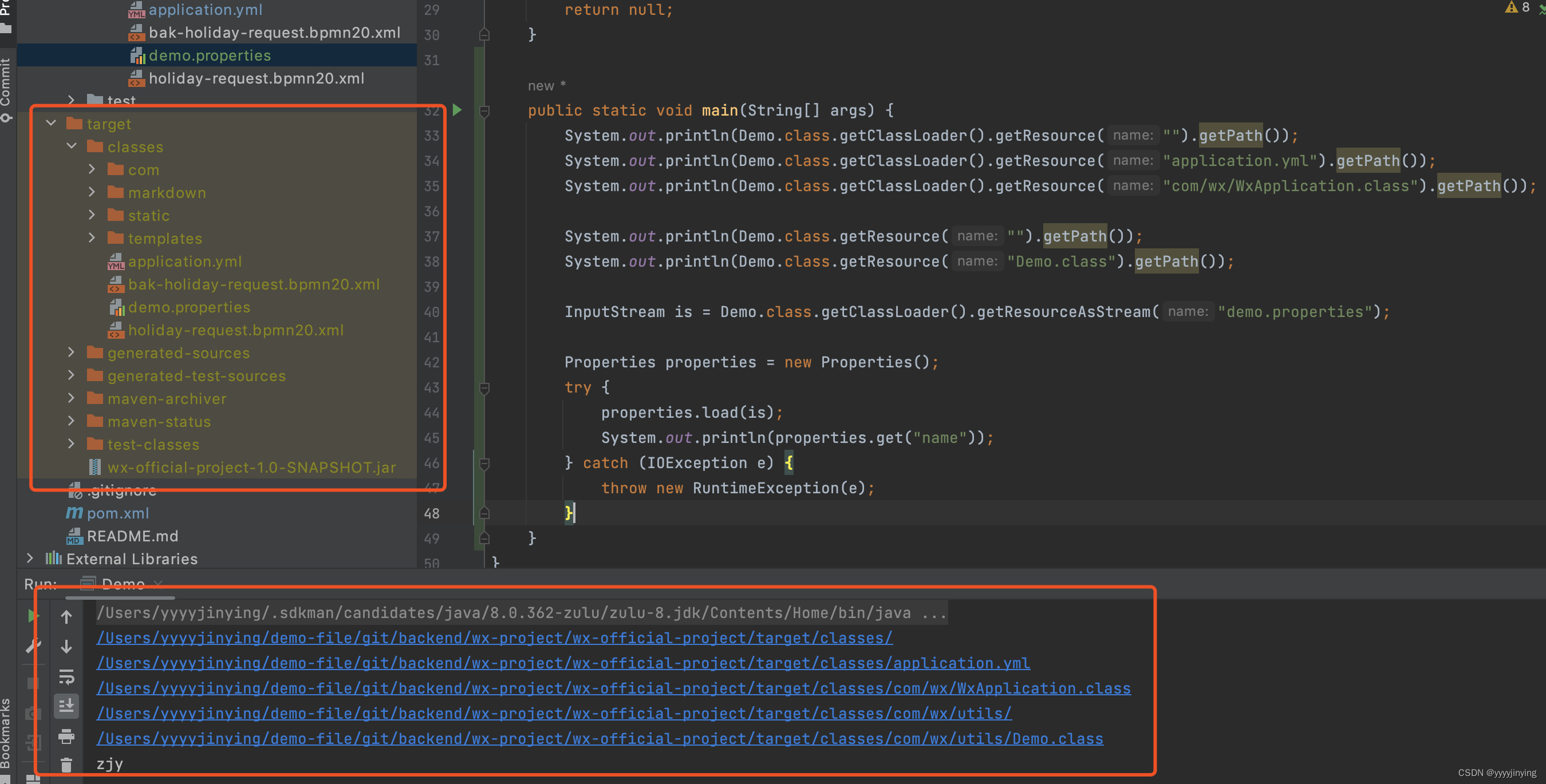
io基础入门
压缩的封装 参考:https://blog.csdn.net/qq_29897369/article/details/120407125?utm_mediumdistribute.pc_relevant.none-task-blog-2defaultbaidujs_baidulandingword~default-0-120407125-blog-120163063.235v38pc_relevant_sort_base3&spm1001.2101.3001.…...
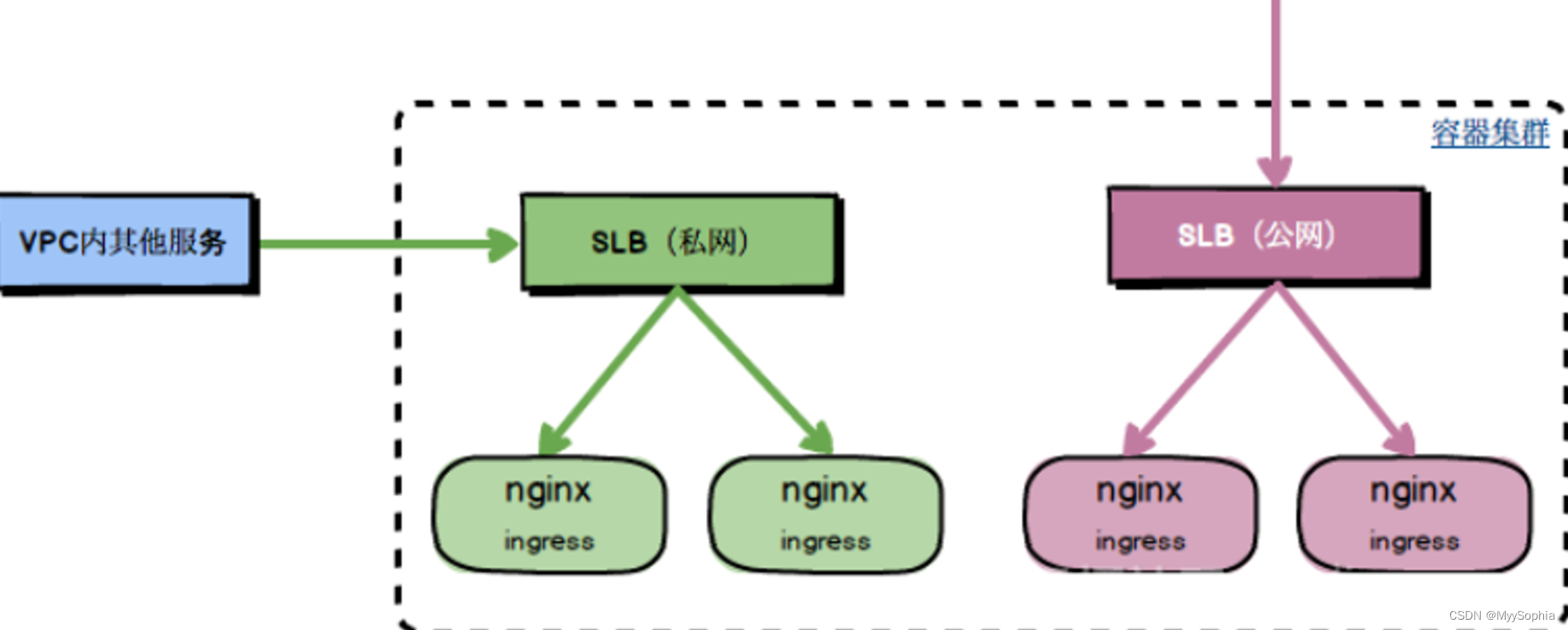
k8s ingress 无法找到端点
文章目录 ingress rule无法找到端点这个注解是什么意思呢?为何不生效呢?端点无法更新?如何确认ingressclass呢?修复端点无法发现的问题多个ingress controller 架构 ingress rule无法找到端点 在vnnox-cn集群创建ingress…...
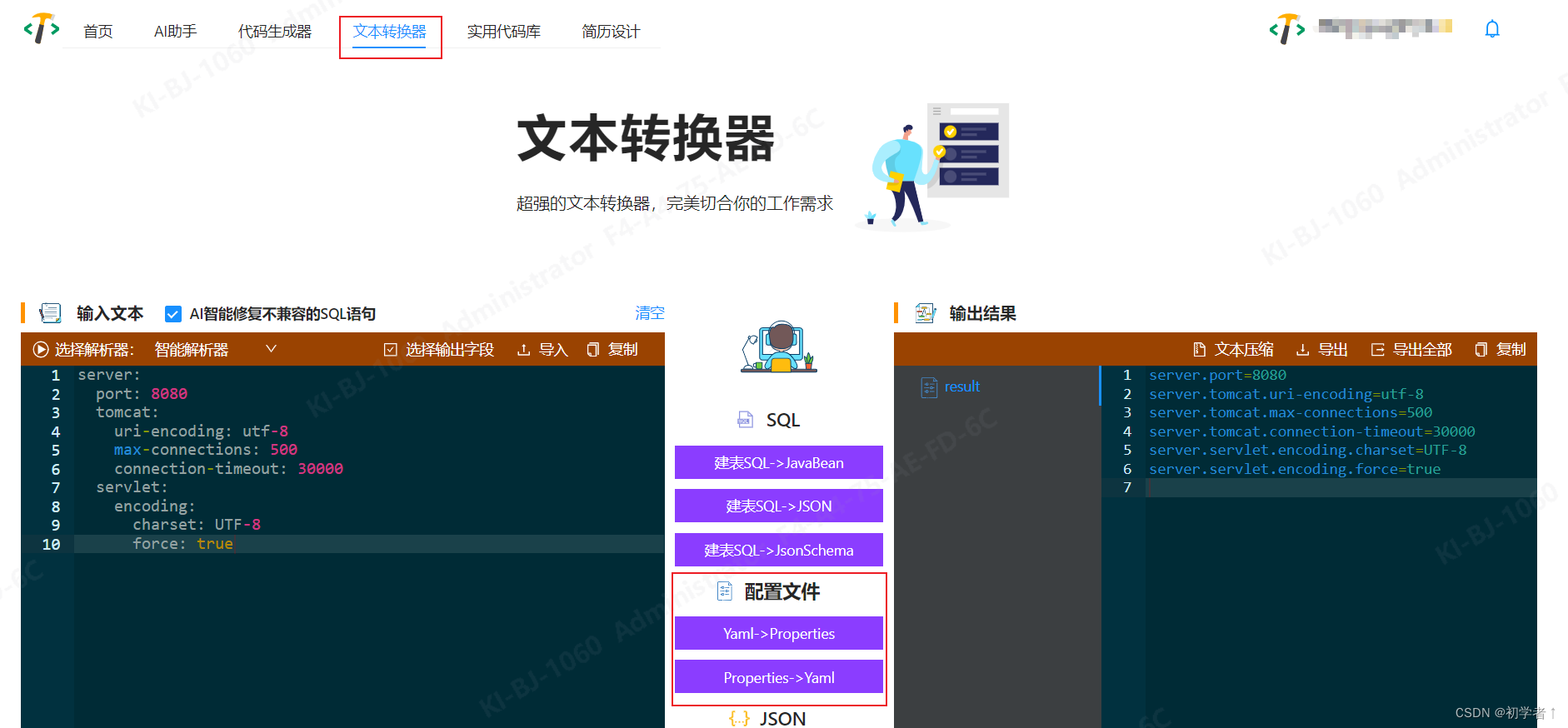
properties转yml
目前搜索到的大部分代码都存在以下问题: 复杂结构解析丢失解析后顺序错乱 所以自己写了一个,经过不充分测试,基本满足使用。可以直接在线使用 在线地址 除了yml和properties互转之外,还可以生成代码、sql转json等,可…...
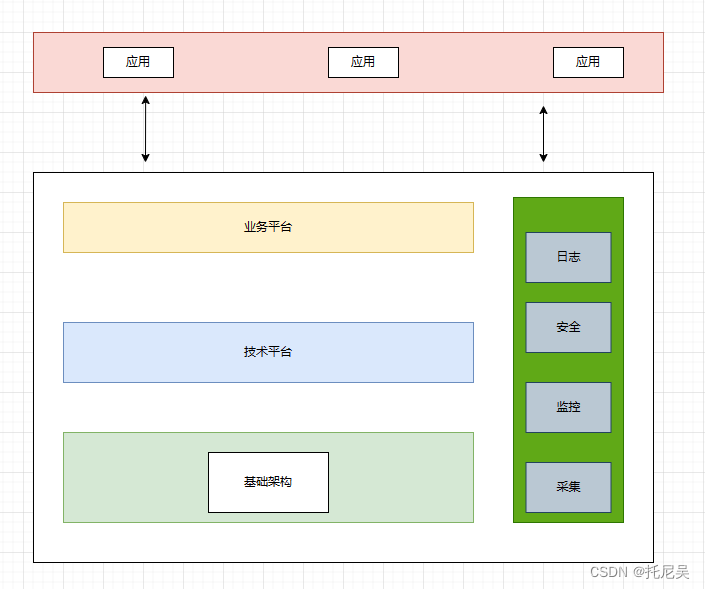
谈谈中间件设计的思路
前言 想要设计和真正理解中间件的架构理论和思想。对于开发来说需要具备三个关键的能力 1:基础通用技术的深入理解和运用2:了解和熟悉常见中间件的设计思想,且有自己的感悟,并且能按照自己的理解模仿写一写3:业务的高度理解能力…...

WT2605-24SS音频蓝牙录放语音芯片:标准蓝牙功能与多样化存储播放方式助力音频体验升级
在音频技术日新月异的今天,WT2605-24SS音频蓝牙录放语音芯片以其强大的功能和出色的性能,成为了音频市场的一颗璀璨明星。该芯片不仅具备标准音频蓝牙功能,还支持蓝牙电话本、录音功能以及多种存储和播放方式,为用户提供了更加便捷…...

openssl生成ssl证书
x509证书一般会用到三类文,key,csr,crt。 Key 是私用密钥openssl格,通常是rsa算法。 Csr 是证书请求文件,用于申请证书。在制作csr文件的时,必须使用自己的私钥来签署申,还可以设定一个密钥。…...
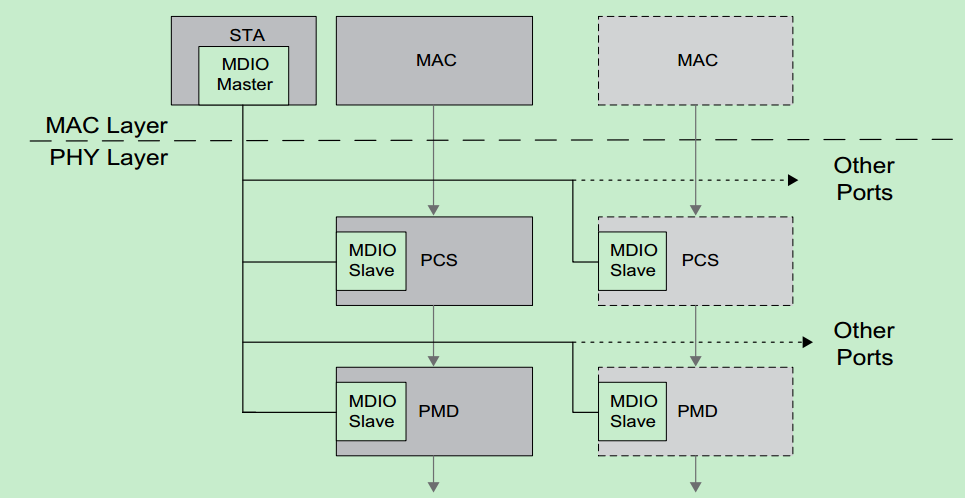
以太网PHY,MAC接口
本文主要介绍以太网的 MAC 和 PHY,以及之间的 MII(Media Independent Interface ,媒体独立接口)和 MII 的各种衍生版本——GMII、SGMII、RMII、RGMII等。 简介 从硬件的角度看,以太网接口电路主要由MAC(M…...

c语言中 , x++ 和 ++x的区别
一 c语言中 , x 和 x的区别 x 和 x 是 C 语言中的自增运算符,它们的区别在于它们的执行时机和返回值: 1. x (后缀自增): 先使用变量的值,然后再将变量的值加 1。这意味着,如果你在一个表达式中使用了 x,那么该表达式…...
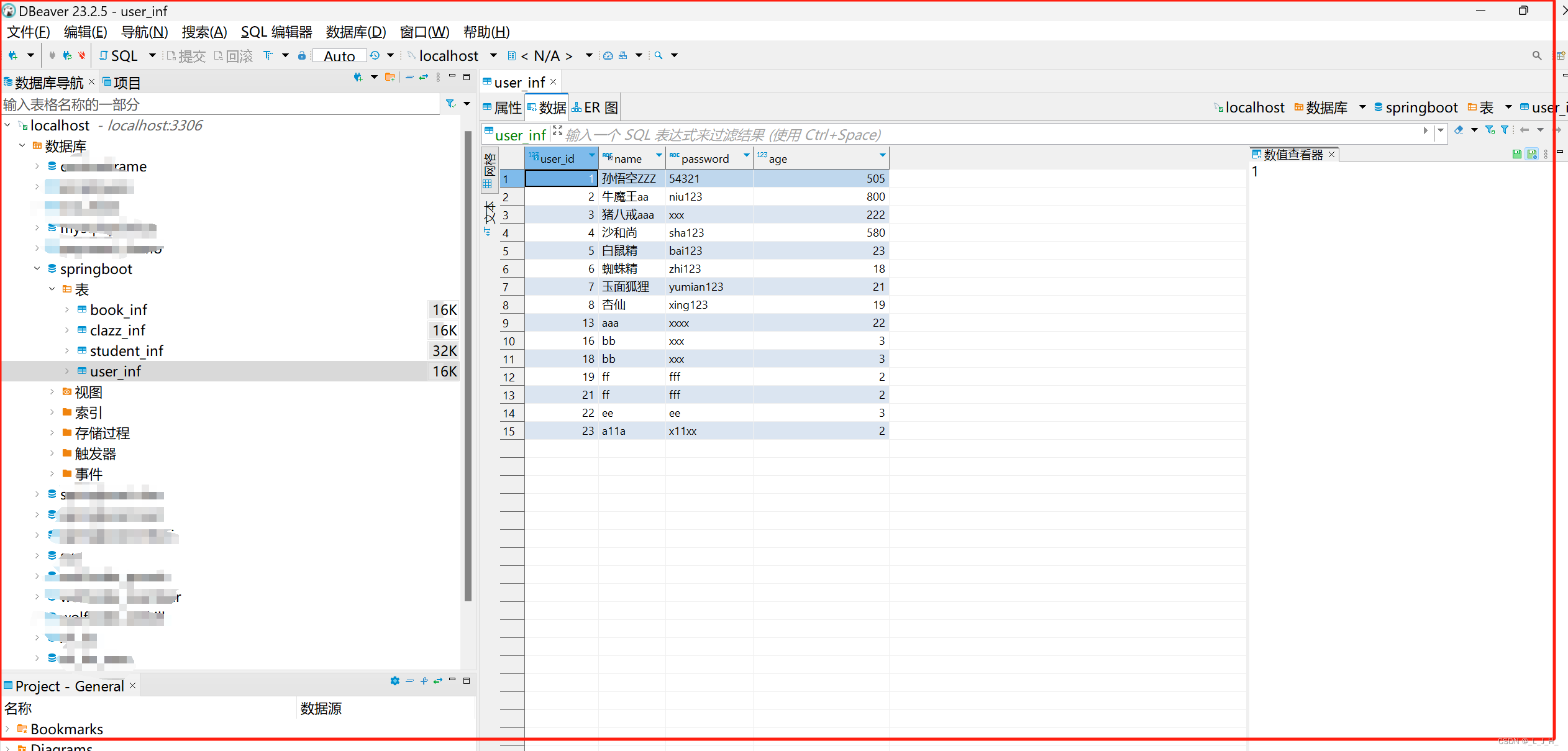
DBeaver 社区版(免费版)下载、安装、解决驱动更新出错问题
DBeaver 社区版(免费版) DBeaver有简洁版,企业版,旗舰版,社区版(免费版)。除了社区版,其他几个版本都是需要付费的,当然相对来说,功能也要更完善些ÿ…...

景联文科技加入中国人工智能产业联盟(AIIA)数据委员会
近日,景联文科技加入中国人工智能产业联盟(AIIA)数据委员会,成为委员会成员单位。 中国人工智能产业发展联盟(简称AIIA)是在国家发改委、科技部、工信部、网信办指导下,由中国信息通信研究院等单…...

数据结构 / 结构体指针
1. 格式 struct 结构体名{数据类型 成员1;数据类型 成员2; .... };struct 结构体名 *指针变量名 2. 结构体指针指向普通变量的地址 struct CAR{char name[10];int price; };struct CAR car{"byd",160}; struct CAR *p&car; //p是指向结构体变量car的指针// p…...
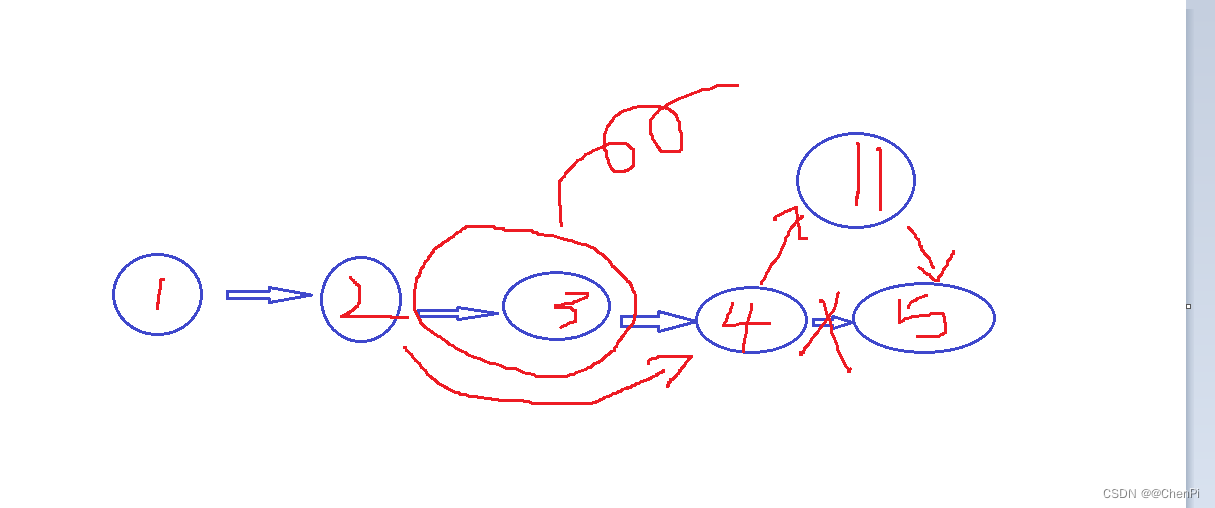
P1 什么是链表 C语言简单易懂
目录 前言 01 什么是链表 02 数组的特点 03 数组的缺点 3.1 删除数组其中一个元素 3.2 数组增加某个节点 04 链表 前言 🎬 个人主页:ChenPi 🐻推荐专栏1: 《 C 》✨✨✨ 🔥 推荐专栏2: 《 Linux C应用编程(概念…...
Python实现FA萤火虫优化算法优化循环神经网络分类模型(LSTM分类算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 萤火虫算法(Fire-fly algorithm,FA)由剑桥大学Yang于2009年提出 , …...

Spring Task
Spring Task 是Spring框架提供的任务调度工具,可以按照约定的时间自动执行某个代码逻辑。 **定位:**定时任务框架 **作用:**定时自动执行某段Java代码 cron表达式 cron表达式其实就是一个字符串,通过cron表达式可以定义任务触…...

HttpServletRequest/Response视频笔记
学习地址:144-尚硅谷-Servlet-HttpServletRequest类的介绍_哔哩哔哩_bilibili 目录 1.HttpServletRequest 类 a.HttpServletRequest类有什么作用 b.HttpServletRequest类的常用方法 c.如何获取请求参数 d.解决post请求中文乱码问题 获取请求的参数值相关问题 …...
网上选课系统源码(Java)
JavaWebjsp网上选课系统源码 运行示意图:...

mac修改默认shell为bash
1. 打开系统偏好设置 2. 点击用户群组 3. 按住ctrl,点击用户名 4. 点击高级选项,修改登录shell 参考:在 Mac 上将 zsh 用作默认 Shell - 官方 Apple 支持 (中国)...

基于Java SSM小区物业管理系统
小区有多栋住宅,每栋楼有多套物业(房屋),物业管理公司提供物业管理服务,业主需要按月缴纳物业费。小区物业管理系统对物业公司的日常工作进行管理。系统管理的对象及操作有: 楼宇信息:楼号、户数、物业费标准。 房屋信…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...
