力扣题:字符串的反转-11.23
力扣题-11.23
[力扣刷题攻略] Re:从零开始的力扣刷题生活
力扣题1:557. 反转字符串中的单词 III
解题思想:先读取单词,然后将单词进行翻转即可

class Solution(object):def reverseWords(self, s):""":type s: str:rtype: str"""word_list = s.split()string = ''for i in range(len(word_list)):string += self.reverse(word_list[i]) + ' 'return string.rstrip()def reverse(self, s):s_list = list(s)for i in range(len(s_list)//2):temp = s_list[i]s_list[i] = s_list[len(s_list)-i-1]s_list[len(s_list)-i-1] = tempreturn ''.join(s_list)
class Solution {
public:string reverseWords(string s) {string result = "";int start = 0;int temp = 0;for (int i = 0; i < s.size(); i++) {if (s[i] != ' ') {temp += 1;} else {result += reverse(s.substr(start, temp)) + ' ';start = i + 1;temp = 0;}}result += reverse(s.substr(start, temp)); return result;}string reverse(const string &s) {string reversed = s;for (int i = 0; i < reversed.size() / 2; i++) {char temp = reversed[i];reversed[i] = reversed[reversed.size() - 1 - i];reversed[reversed.size() - 1 - i] = temp;}return reversed;}
};
相关文章:

力扣题:字符串的反转-11.23
力扣题-11.23 [力扣刷题攻略] Re:从零开始的力扣刷题生活 力扣题1:557. 反转字符串中的单词 III 解题思想:先读取单词,然后将单词进行翻转即可 class Solution(object):def reverseWords(self, s):""":type s…...

【软件测试】盘一盘工作中遇到的 Redis 异常测试
在测试工作中,涉及到与 redis 交互的场景变的越来越多了。关于redis本身就不作赘述了,网上随便搜,本人也做过一些整理。 今天只来复盘一下,在测试过程中与 redis 的二三事儿。其中提到的案例是经过抽象化的,用作辅助说…...

14.Oracle中RegExp_Like 正则表达式基本用法
--基本用法,是否包含某字符串 like %36% select * from k_micfo where regexp_like(loginid,36);if regexp_like(str,^[0-9\.]$) --只包含数字0-9,,小数点.--oracle判断字段是否是纯数字 (四种写法结果一样) select * from k_micfo where r…...
Docker Swarm总结+Jenkins安装配置与集成(5/5)
博主介绍:Java领域优质创作者,博客之星城市赛道TOP20、专注于前端流行技术框架、Java后端技术领域、项目实战运维以及GIS地理信息领域。 🍅文末获取源码下载地址🍅 👇🏻 精彩专栏推荐订阅👇🏻…...
docker安装Sentinel zipkin
文章目录 引言I Sentinel安装1.1 运行容器1.2 DOCKERFILE 参考1.3 pom 依赖1.4 .yml配置(整合springboot)II 资源保护2.1 Feign整合Sentinel2.2 CommonExceptionAdvice:限流异常处理类III zipkin引言 消息服务和请求第三方服务可不配置Sentinel。 </...

利用python实现文件压缩打包的功能
主要是利用了zipfile实现文件压缩打包,简单实例代码如下: import zipfilewith zipfile.ZipFile("archive.zip",w) as zipf:zipf.write("config.ini")zipf.write("test.py") 其中的模式 w表示如果没有该文件则创建该文件…...

如何创建百科?建立百科词条的意义何在?九问百科营销
在营销工作实践中,小马识途营销顾问经常接到关于百科营销的咨询,现整理了最受关注的九个问题分享给热爱营销工作的小伙伴。 一、什么是百科营销? 百科营销是借助百科知识传播,可以将企业、品牌、人物所拥有的对用户有价值的信息&a…...

Django如何设置时区为北京时间?
Django默认使用的是UTC时间,北京时间比UTC早8个小时,即如果UTC是凌晨两点,那么北京时间是早上八点。 Django中把setting.py中的语句: TIME_ZONE UTC修改为: TIME_ZONE Asia/Shanghai就把时区改为了北京时间。 这…...
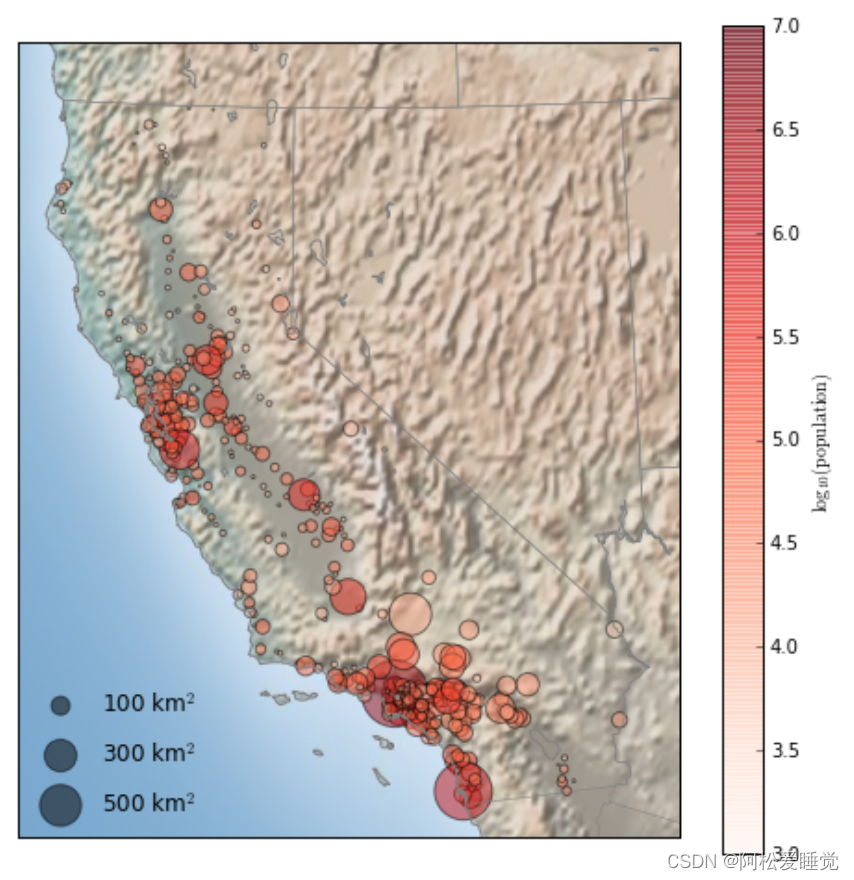
Basemap地图绘制_Python数据分析与可视化
Basemap地图绘制 安装和使用地图投影地图背景在地图上画数据 Basemap是Matplotlib的一个子包,负责地图绘制。在数据可视化过程中,我们常需要将数据在地图上画出来。 比如说我们在地图上画出城市人口,飞机航线,军事基地,…...
)
C#编程题分享(5)
判断质数问题 输⼊⼀个正整数,判断该数是否是质数。如果为质数输出 yes,如果不是输出no 样例输⼊113 输出yes int n Convert.ToInt32(Console.ReadLine()); int count 0; for (int i 1; i < n 1; i) {if (n % i 0) // 判断该数能被整除{coun…...
群晖Video Station 添加海报墙-新方法
海报墙 一般我们找到的都是mp4、mkv等格式的视频资源,而没有像上图这样的海报资源,那要怎样实现海报墙呢? 按照以前的方法,是可以通过The Movie Database的API Key来搜刮电影海报信息,但是现在这个方法不行了 现在介绍…...

【MODBUS】Modbus协议入门简介
Modbus(Modicon Communication Protocol)是一种用于工业自动化领域的通信协议,最初由Modicon(现在是施耐德电气的一部分)开发。Modbus协议被广泛应用于连接不同厂商的工业设备,实现设备之间的通信和数据交换…...
ORA-00257: archiver error. Connect internal only, until freed……
今天给客户测 试问题,让客户把数据发过来了。解压缩后一看,他们还是用的oracle 815版本的(他们exp导出时,带了导出日志,从导出日志中看出来是oracle 815版本的),不过没有关系,低版本的exp是可以用高版本的i…...
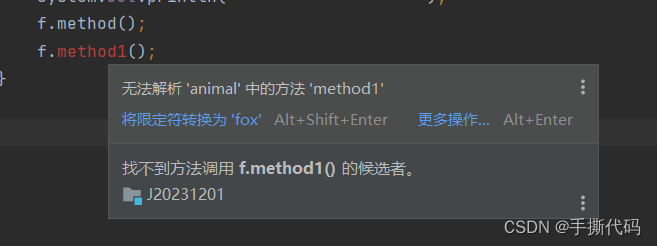
继承 和 多肽(超重点 ! ! !)
[本节目标] 1.继承 2.组合 3.多肽 1.继承 1.1 为什么要继承 Java中使用类对现实世界中实体来进行描述,类经过实例化之后的产物对象,则可以用来表示现实中的实体,但是现实世界错综复杂,事物之间可能会存在一些关联࿰…...

H265、VP9、AV1视频编码器性能对比
1、背景介绍 目前在视频编解码器中,H264 已经成为绝对的主流,被大部分设备、浏览器所支持。虽然有更先进的编码器推出,但是受限于推广速度和设备支持成本,一直未能成为主流。 今年公司的目标是持续降本增效,现在将”屠刀“指向了视频业务的存储成本。视频文件存储主要两…...

C语言-结构体
---------------------------- ------------------ 岁月漫长心怀热爱,携手共赴星辰大海 --------今天来到我们自定义类型 -----结构体的讲解 目录 结构体的类型声明和初始化 结构体的类型声明 结构体成员的直接访问 结构体成员的间接访问 嵌套结构体进行访问 使用…...

C#拼夕夕自动化登录,电商网页自动化操作。WebView2
单纯靠WebView2是没办法通过JS实现自动登录操作的,包括浏览器插件,都不行,因为大公司对反爬机制控制的还是挺严格。 下面是实现效果,私信我,咨询解决方案。 20231202_153912 C#有偿Q群:927860652博客仅为…...

【Spring Boot 源码学习】BootstrapRegistryInitializer 详解
Spring Boot 源码学习系列 BootstrapRegistryInitializer 详解 引言往期内容主要内容1. 初识 BootstrapRegistryInitializer2. 加载 BootstrapRegistryInitializer3. BootstrapRegistryInitializer 的初始化 总结 引言 书接前文《初识 SpringApplication》,我们从 …...
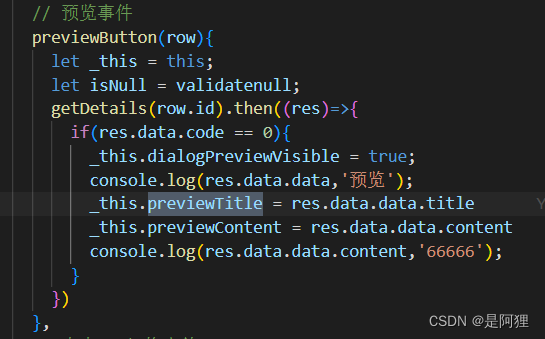
预览功能实现
需求:将后端返回来的文字或者图片和视频展示在页面上。 <!-- 预览 --><el-dialog title"预览" :visible.sync"dialogPreviewVisible" width"50%" append-to-body :close-on-click-modal"false" close"Previe…...

canvas基础:绘制贝塞尔曲线
canvas实例应用100 专栏提供canvas的基础知识,高级动画,相关应用扩展等信息。 canvas作为html的一部分,是图像图标地图可视化的一个重要的基础,学好了canvas,在其他的一些应用上将会起到非常重要的帮助。 文章目录 bez…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
