数据结构之堆排序以及Top-k问题详细解析
个人主页:点我进入主页
专栏分类:C语言初阶 C语言程序设计————KTV C语言小游戏 C语言进阶
C语言刷题 数据结构初阶
欢迎大家点赞,评论,收藏。
一起努力
目录
1.前言
2.堆排序
2.1降序排序
2.2时间复杂度
3.Top-k问题
4.总结
1.前言
在上一篇文章中我们主要讲解了关于大堆和小堆的代码实现,今天我们主要讲解关于堆排序以及堆排序的时间复杂度,我们会讲解关于经典的Top-k问题进行讲解(其中我会伪造一些数据来展示),今天的内容比上次的内容更加的爽,更有挑战性,其中的奥妙真的无法用语言来形容,接下来就让我们感受一下吧。
2.堆排序
我们对数组进行降序排序,我们使用堆排序,在这里由于升序和降序的思想基本一致,只需要修改一些符号即可完成转化,所以我们只讲关于降序的内容。
2.1降序排序
在上次的内容中我们使用向上调整来创建堆,我们是创建小堆还是大堆呢?我们想让数据进行降序,如果我们使用大堆的话堆的第一个数是最大的,我们取出来之后堆的顺序就乱了,我们需要重新进行大堆排序,那么我们的时间复杂度为O(n^2*logn),这比我们的冒泡排序还要慢,所以大堆是不可以的,所以我们选择小堆排序,我们这次依旧使用想上调整,详细代码如下:
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<assert.h>
void Swap(int* num1, int* num2)
{int temp = *num1;*num1 = *num2;*num2 = temp;
}
void print(int* arr, int size)
{for (int i = 0; i < size; i++)printf("%d ", arr[i]);
}
void AdJustUp(int* arr, int sz,int size)
{assert(arr);int child = sz, parent = (child - 1) / 2;while (child>0){if (arr[child] < arr[parent]){Swap(&arr[child], &arr[parent]);child = parent;parent = (child - 1) / 2;}elsebreak;}
}
void AdJustDown(int* arr, int i, int size)
{assert(arr);int parent = i, child = 2 * parent + 1;while (child<size){if (child + 1 < size && arr[child] >arr[child + 1]){child++;}if (arr[parent] > arr[child]){Swap(&arr[parent], &arr[child]);parent = child;child = 2 * parent + 1;}elsebreak;}
}
void HeapSort(int* arr, int n)
{assert(arr);for (int i = 0; i < n; i++){AdJustUp(arr, i, n);}for (int i = 0; i < n-1; i++){Swap(&arr[0], &arr[n - 1 - i]);AdJustDown(arr, 0, n - 1 - i);}}
int main()
{int arr[10];int n = 10;for (int i = 0; i < n; i++){arr[i] = i;}HeapSort(arr,n);print(arr, n);return 0;
}我们的运行结构如下:
![]()
事实上我们这不是我们的堆排序,真正的堆排序在第一次创建小堆时代码为:
for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdJustDown(arr, 0, n - 1 - i);}向下调整为什么可以实现呢?,我们知道向下调整是左边和右边都是小堆然后根节点是新插入的我们就可以利用向下调整进行排序,那我们在最后一个节点的父节点进行向下调整,让他们都成为小堆,这样我们就可以完成小堆的创建。那为什么采用这种形式呢?仅仅是因为代码少吗?事实上这与我们的时间复杂度有关。
2.2时间复杂度
我们看利用向上调整建立小堆的时间复杂度,我们第k层有2^(k-1)个节点,每个节点需要向上调整k-1次共调整(k-1)*2^(k-1)次,第k-1层有2^(k-2),每个节点需要调整k-2次,共调整(k-2)*2^(k-2)……第二层有2^1个节点,每个节点需要调整1次,第一层有2^0个节需要调整0次,共需要调整T(k)=0*2^0+1*2^1+……+(k-2)*2^(k-2)+(k-1)*2^(k-1),我们化简可以得到T(k)=(k-2)2^k+2;其中k=logN,所以T(k)=NlogN;但是我们采用向下调整我们第k层有我们第k层有2^(k-1)个节点,每个节点需要向上调整0次共调整0*2^(k-1)次,第k-1层有2^(k-2),每个节点需要调整1次,共调整1*2^(k-2)……第二层有2^1个节点,每个节点需要调整k-2次,第一层有2^0个节需要调整k-1次,共需要调整T(k)=(k-1)*2^0+(k-2)*2^1+……+1*2^(k-2)+0*2^(k-1),我们化简得到T(k)=2^k-k-1,其中k=logN,故T(k)=N-logN;可以看到向下调整建立堆时间复杂度低,所以我们选择向下调整这大大减少了我们的运算时间。
3.Top-k问题
有一个问题是我们在一组数中(共N个数)找到最小的k个数,其中N远大于k,让我们找到前k个数,当数据很小的时候我们利用堆排序进行查找很容易,但是当数据量特别大的时候我们就很难实现,因为数据占用的内存太大了,例如我们要在1百亿个数据中找到前10个最小的数,100万个整形数据相当于占用37GB,这样我们就很难处理,这时候就出现了我们的Top-k问题,我们是如何解决这个问题呢?这时候我们由于需要找最小的前10个数据我们创建一个大堆,然后输入一个数据就将堆顶元素替换然后再向下调整这样就可以找到最小的10个数据,我们创建100万个数据进行模拟,我们的代码如下:
我们将数据放在文件中,生成data.txt文件
#include<stdio.h>
int main()
{FILE* pf = fopen("data.txt", "w");if (pf == NULL){perror("fopen fail");return 1;}for (int i = 0; i < 1000000; i++){fprintf(pf,"%d\n", i);}fclose(pf);pf = NULL;return 0;
}修改其中的10个数据让他成为我们的结果,然后进行下一步找到这k个数
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>
typedef int MyHeapData;
typedef struct Heap {MyHeapData* data;int size;int capacity;
}Heap;
void HeapInit(Heap* php)
{assert(php);php->data = (MyHeapData*)malloc(sizeof(MyHeapData)*10);php->size = 0;
}
void Swap(int* num1, int* num2)
{int temp = *num1;*num1 = *num2;*num2 = temp;
}
void AdJustDown(int* arr, int n, int i)
{assert(arr);int parent = 0, child = 2 * parent + 1;while (child<n){if (child+1<n&&arr[child] < arr[child + 1]){child++;}if (arr[parent] < arr[child]){Swap(&arr[parent], &arr[child]);parent = child;child = parent * 2 + 1;}elsebreak;}
}
void AdJustUp(MyHeapData* arr, int size)
{assert(arr);int child = size - 1, parent = (child - 1) / 2;while (child > 0){if (arr[child] > arr[parent]){Swap(&arr[child], &arr[parent]);child = parent;parent = (child - 1) / 2;}elsebreak;}
}
int main()
{//FILE* pf = fopen("data.txt", "w");//if (pf == NULL)//{// perror("fopen fail");// return 1;//}//for (int i = 0; i < 1000000; i++)//{// fprintf(pf,"%d\n", i);//}//fclose(pf);//pf = NULL;FILE* pf = fopen("data.txt", "r");if (pf == NULL){perror("fopen fail");return 1;}int data;int i;Heap ph ;HeapInit(&ph);for (i = 0; i < 10; i++){fscanf(pf, "%d", &data);ph.data[i] = data;AdJustUp(ph.data, i);}while (fscanf(pf, "%d", &data) != EOF){if(data<ph.data[0])Swap(&data, &ph.data[0]);AdJustDown(ph.data, 10, 0);}for (i = 0; i < 10; i++){printf("%d ", ph.data[i]);}fclose(pf);pf = NULL;return 0;
}运行结果如下:

这就是我们经典的Top-k问题;
4.总结
今天的内容到这里就结束了,希望大家可以好好的理解今天的内容,欢迎大家来三连。
相关文章:

数据结构之堆排序以及Top-k问题详细解析
个人主页:点我进入主页 专栏分类:C语言初阶 C语言程序设计————KTV C语言小游戏 C语言进阶 C语言刷题 数据结构初阶 欢迎大家点赞,评论,收藏。 一起努力 目录 1.前言 2.堆排序 2.1降序排序 2.2时间复杂…...

ESP32-Web-Server 实战编程-通过网页控制设备多个 GPIO
ESP32-Web-Server 实战编程-通过网页控制设备多个 GPIO 概述 上节 ESP32-Web-Server 实战编程-通过网页控制设备的 GPIO 讲述了如何通过网页控制一个 GPIO。本节实现在网页上控制多个 GPIO。 示例解析 前端设计 前端代码建立了四个 GPIO,如下死 GPIO 2 在前端的…...

说一说MySQL中的锁机制
说一说MySQL中的锁机制 按粒度大小从大到小分为 全局锁 全局锁 全局锁是对整个数据库的锁,最常用的全局锁就是读写锁 读锁 阻止其他用户更新数据,允许其他用户读数据写锁 阻止其他用户更新和读数据 修改一些大量的数据,并且不希望其他用户…...
C++笔试训练day_1
文章目录 选择题编程题 选择题 编程题 #include <iostream> #include <algorithm> #include <vector>using namespace std;int main() {int n 0;cin >> n;vector<int> v;v.resize(3 * n);int x 0;for(int i 0; i < v.size(); i){cin >&…...
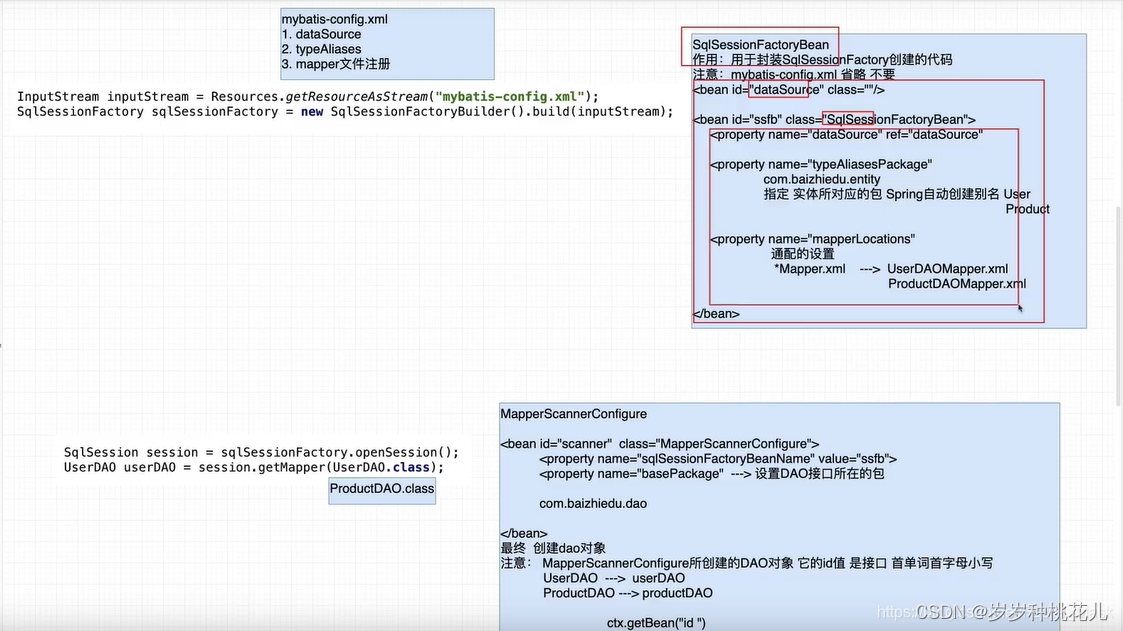
详解Spring对Mybatis等持久化框架的整合
😉😉 学习交流群: ✅✅1:这是孙哥suns给大家的福利! ✨✨2:我们免费分享Netty、Dubbo、k8s、Mybatis、Spring...应用和源码级别的视频资料 🥭🥭3:QQ群:583783…...

[Electron] 将应用打包成供Ubuntu、Debian平台下安装的deb包
在使用 electron-packager 工具输出 linux 平台的 electron app 后,可以使用 electron-installer-debian 工具把 app 打包成供Ubuntu平台下安装的 debian 包。 electron-installer-debian是一个用于创建 Debian Linux(.deb)安装包的开发工…...

7.24 SpringBoot项目实战【审核评论】
文章目录 前言一、编写控制器二、编写服务层三、Postman测试前言 我们在 上文 7.23 已经实现了 评论 功能,本文我们继续SpringBoot项目实战 审核评论 功能。逻辑如下: 一是判断管理员权限,关于角色权限校验 在 7.5 和 7.6 分别基于 拦截器Interceptor 和 切面AOP 都实现过…...
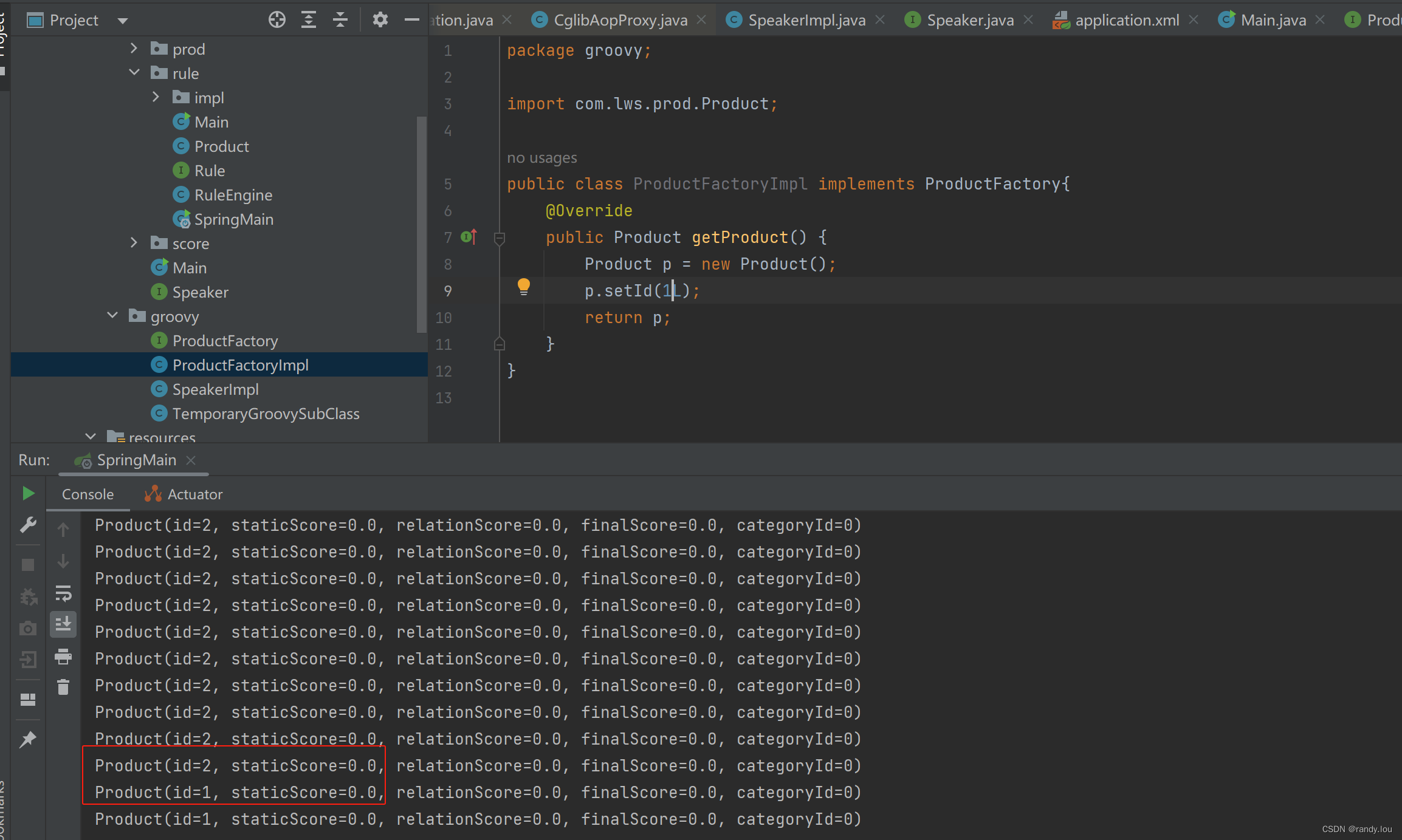
Java实现动态加载的逻辑
日常工作中我们经常遇到这样的场景,某某些逻辑特别不稳定,随时根据线上实际情况做调整,比如商品里的评分逻辑,比如规则引擎里的规则。 常见的可选方案有: JDK自带的ScriptEngine 使用groovy,如GroovyClassLoader、Gro…...

数据库的设计规范
文章目录 第一范式(1NF):列不可再分 第二范式 (2NF):所有非主键字段,都必须 完全依赖主键,不能部分依赖 第三范式(3NF):所有非主键字段不能依赖于…...

正则表达式从放弃到入门(2):grep命令详解
正则表达式从放弃到入门(2):grep命令详解 总结 本博文转载自 这是一篇”正则表达式”扫盲贴,如果你还不理解什么是正则表达式,看这篇文章就对了。 如果你是一个新手,请从头阅读这篇文章,如果你…...
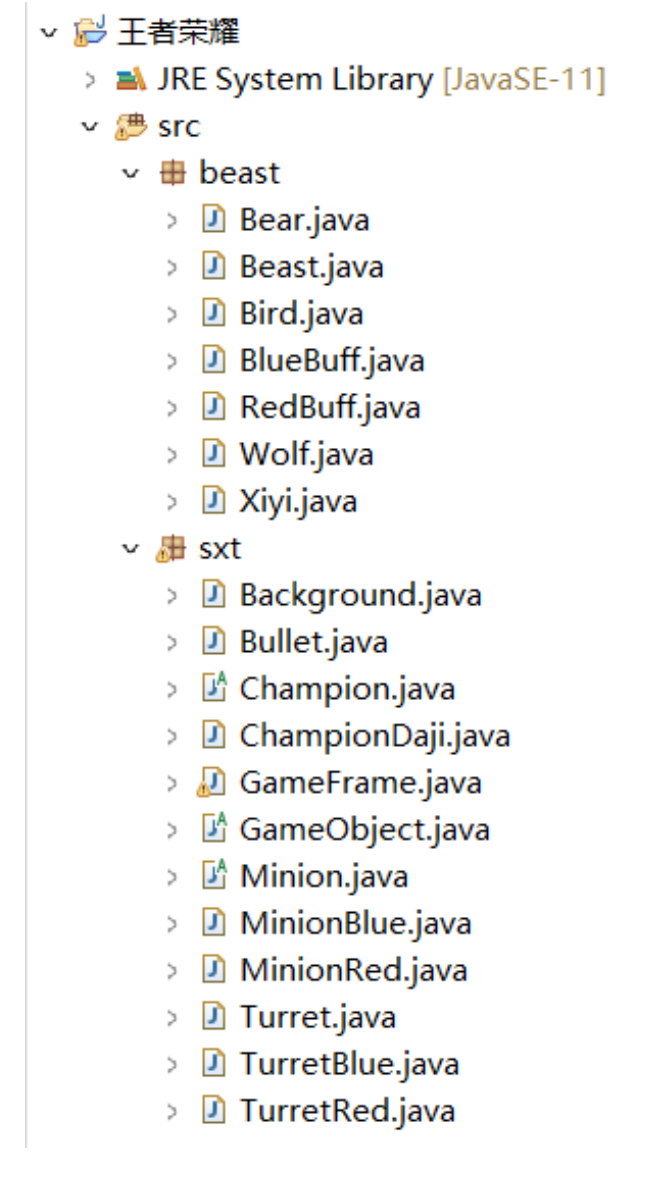
用Java写一个王者荣耀游戏
目录 sxt包 Background Bullet Champion ChampionDaji GameFrame GameObject Minion MinionBlue MinionRed Turret TurretBlue TurretRed beast包 Bear Beast Bird BlueBuff RedBuff Wolf Xiyi 打开Eclipse创建图片中的几个包 sxt包 Background package sxt;…...
基于SSM的新闻网站浏览管理实现与设计
基于ssm的新闻网站浏览管理实现与设计 摘要:在大数据时代下,科技与技术日渐发达的时代,人们不再局限于只获取自己身边的信息,而是对全球信息获取量也日渐提高,网络正是打开这新世纪大门的钥匙。在传统方式下ÿ…...
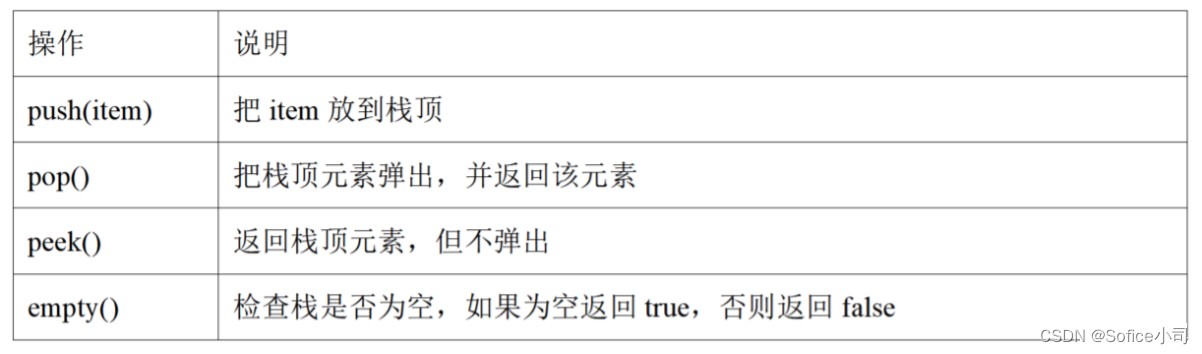
【蓝桥杯软件赛 零基础备赛20周】第6周——栈
文章目录 1. 基本数据结构概述1.1 数据结构和算法的关系1.2 线性数据结构概述1.3 二叉树简介 2. 栈2.1 手写栈2.2 CSTL栈2.3 Java 栈2.4 Python栈 3 习题 1. 基本数据结构概述 很多计算机教材提到:程序 数据结构 算法。 “以数据结构为弓,以算法为箭”…...

CWE/SANS TOP 25 2022
我整理了CWE/SANS TOP25 2022年的这25类缺陷,分类适合的开发语言,其实主要是C/C语言的缺陷相对于Java、PHP、Python、C#等更高级的语言的不同,所以分为适合C/C语言和其它语言。但是大家不要纠结,例如SQL难道C/C语言程序没有吗&…...

Qt 天气预报项目
参考引用 QT开发专题-天气预报 1. JSON 数据格式 1.1 什么是 JSON JSON (JavaScript Object Notation),中文名 JS 对象表示法,因为它和 JS 中对象的写法很类似 通常说的 JSON,其实就是 JSON 字符串,本质上是一种特殊格式的字符串…...

新知识-Tuple元组的使用
文章目录 前言一、tuple元组是什么?二、解决方法总结 前言 这次碰到一个需求,大致需要把表A中的字段1和字段2作为共同的表去查表B,并且一次性需要查多条,一开始是想的是根据字段1和字段2去查然后循环多次,但是这样反复…...

“此应用专为旧版android打造,因此可能无法运行”,问题解决方案
当用户在Android P系统上打开某些应用程序时,可能会弹出一个对话框,提示内容为:“此应用专为旧版Android打造,可能无法正常运行。请尝试检查更新或与开发者联系”。 随着Android平台的发展,每个新版本通常都会引入新的…...

【Leetcode题单】(01 数组篇)刷题关键点总结03【数组的改变、移动】
【Leetcode题单】(01 数组篇)刷题关键点总结03【数组的改变、移动】(3题) 数组的改变、移动453. 最小操作次数使数组元素相等 Medium665. 非递减数列 Medium283. 移动零 Easy 大家好,这里是新开的LeetCode刷题系列&…...
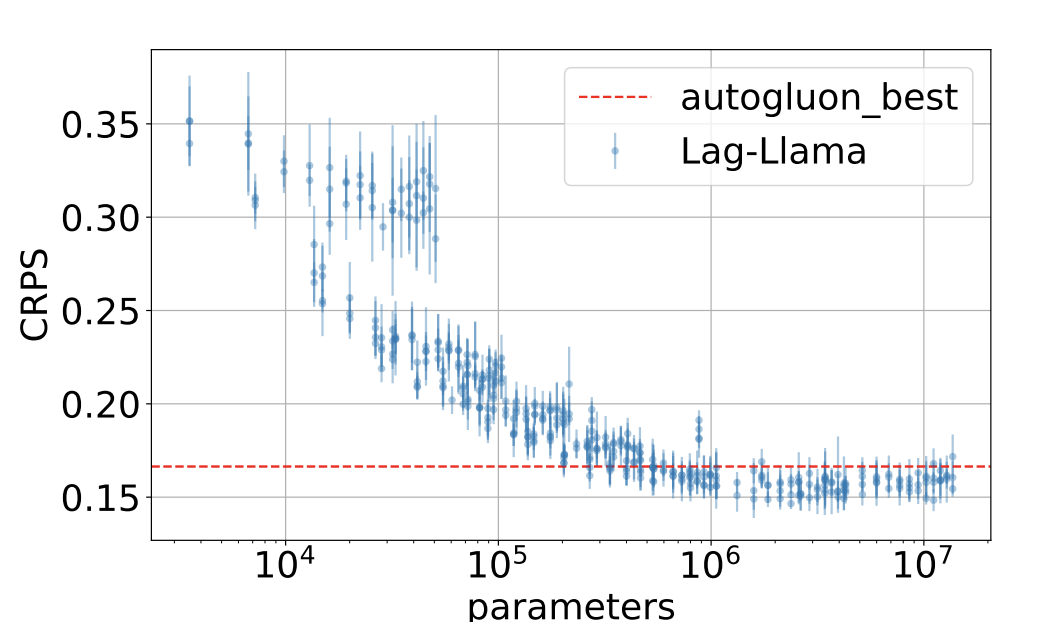
Lag-Llama:基于 LlaMa 的单变量时序预测基础模型
文章构建了一个通用单变量概率时间预测模型 Lag-Llama,在来自Monash Time Series库中的大量时序数据上进行了训练,并表现出良好的零样本预测能力。在介绍Lag-Llama之前,这里简单说明什么是概率时间预测模型。概率预测问题是指基于历史窗口内的…...
 深度选择器不生效)
vue3 :deep() 深度选择器不生效
vue3 :deep() 深度选择器不生效 问题出在根节点上,如果没有这个根节点,那么:deep()不起作用,我把根节点加上,:deep()样式就生效了。在组件外加个 就生效了 参考: 添加链接描述...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

Java后端检查空条件查询
通过抛出运行异常:throw new RuntimeException("请输入查询条件!");BranchWarehouseServiceImpl.java // 查询试剂交易(入库/出库)记录Overridepublic List<BranchWarehouseTransactions> queryForReagent(Branch…...
