【Leetcode题单】(01 数组篇)刷题关键点总结03【数组的改变、移动】
【Leetcode题单】(01 数组篇)刷题关键点总结03【数组的改变、移动】(3题)
- 数组的改变、移动
- 453. 最小操作次数使数组元素相等 Medium
- 665. 非递减数列 Medium
- 283. 移动零 Easy
大家好,这里是新开的LeetCode刷题系列,以后尽量一天更新一个小章节。此系列应超过400题。
数组篇03《数组的改变、移动》,共3道题,1简单题2中等题。
注意看重点部分,总结起来是这一类题的规律。
数组的改变、移动
453. 最小操作次数使数组元素相等 Medium
453. 最小操作次数使数组元素相等

public int minMoves(int[] nums) {int min = Arrays.stream(nums).min().getAsInt();int sum = 0;int n = nums.length;for(int i = 0; i < n; i++){sum += nums[i] - min;}return sum;}
重点
- 问题转化:n-1位加一转换成 1位-1
- Arrays的流操作
665. 非递减数列 Medium
665. 非递减数列

public boolean checkPossibility(int[] nums) {int n = nums.length;int time = 0;for(int i = 1; i < n; i++){int x = nums[i-1], y = nums[i];if(x > y){time++;if(i > 1 && y < nums[i - 2]){nums[i] = x;}if(time > 1){return false;} }}return true;}
重点
- 简化题目:用x,y来指代递减的两个数
- 改变原数组一次,以观察是否符合题设
- 分情况讨论:
- 如果y大于x左侧,则该错误略过
- 如果y小于x左侧,则此时y应修改为x,判断后面序列情况
283. 移动零 Easy
283. 移动零

public void moveZeroes(int[] nums) {int n = nums.length;int tail = 0;for(int num : nums){if(num != 0){nums[tail++] = num;}}for(int i = tail; i < n; i++){nums[i] = 0;}}
重点
- 指针思维,使用指针的思维方式,用tail指向该更新的位置
- 最后别忘记结果置0
这个系列希望能够帮助大家提高刷题效率,发现系列算法题目的常规思路,更快a题,速通Leetcode
b站【软件柠檬】以后会不定期分享计算机领域基础知识,求职干货,为大家助力实习和春秋招offer,
公众号【软件柠檬】也会不定期更新优质内容,分享优质干货资料,希望能够帮助到大家~
❤️这里是 软件柠檬, 让我们一起学习进步~❤️
相关文章:

【Leetcode题单】(01 数组篇)刷题关键点总结03【数组的改变、移动】
【Leetcode题单】(01 数组篇)刷题关键点总结03【数组的改变、移动】(3题) 数组的改变、移动453. 最小操作次数使数组元素相等 Medium665. 非递减数列 Medium283. 移动零 Easy 大家好,这里是新开的LeetCode刷题系列&…...
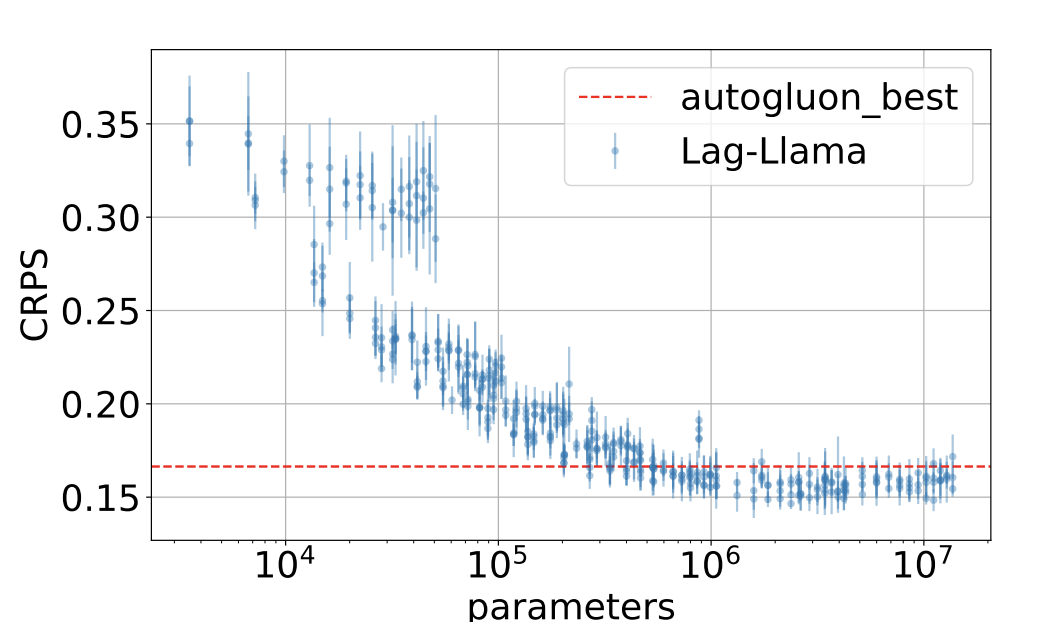
Lag-Llama:基于 LlaMa 的单变量时序预测基础模型
文章构建了一个通用单变量概率时间预测模型 Lag-Llama,在来自Monash Time Series库中的大量时序数据上进行了训练,并表现出良好的零样本预测能力。在介绍Lag-Llama之前,这里简单说明什么是概率时间预测模型。概率预测问题是指基于历史窗口内的…...
 深度选择器不生效)
vue3 :deep() 深度选择器不生效
vue3 :deep() 深度选择器不生效 问题出在根节点上,如果没有这个根节点,那么:deep()不起作用,我把根节点加上,:deep()样式就生效了。在组件外加个 就生效了 参考: 添加链接描述...

从零构建属于自己的GPT系列1:数据预处理(文本数据预处理、文本数据tokenizer、逐行代码解读)
🚩🚩🚩Hugging Face 实战系列 总目录 有任何问题欢迎在下面留言 本篇文章的代码运行界面均在PyCharm中进行 本篇文章配套的代码资源已经上传 从零构建属于自己的GPT系列1:文本数据预处理 从零构建属于自己的GPT系列2:语…...

c++中函数的引用
函数中的引用 引用可以作为函数的形参 不能返回局部变量的引用 #include<iostream> #include<stdlib.h> using namespace std; //形参是引用 void swap(int *x, int *y)//*x *y表示对x y取地址 { int tmp *x; *x *y; *y tmp; } void test01() { …...
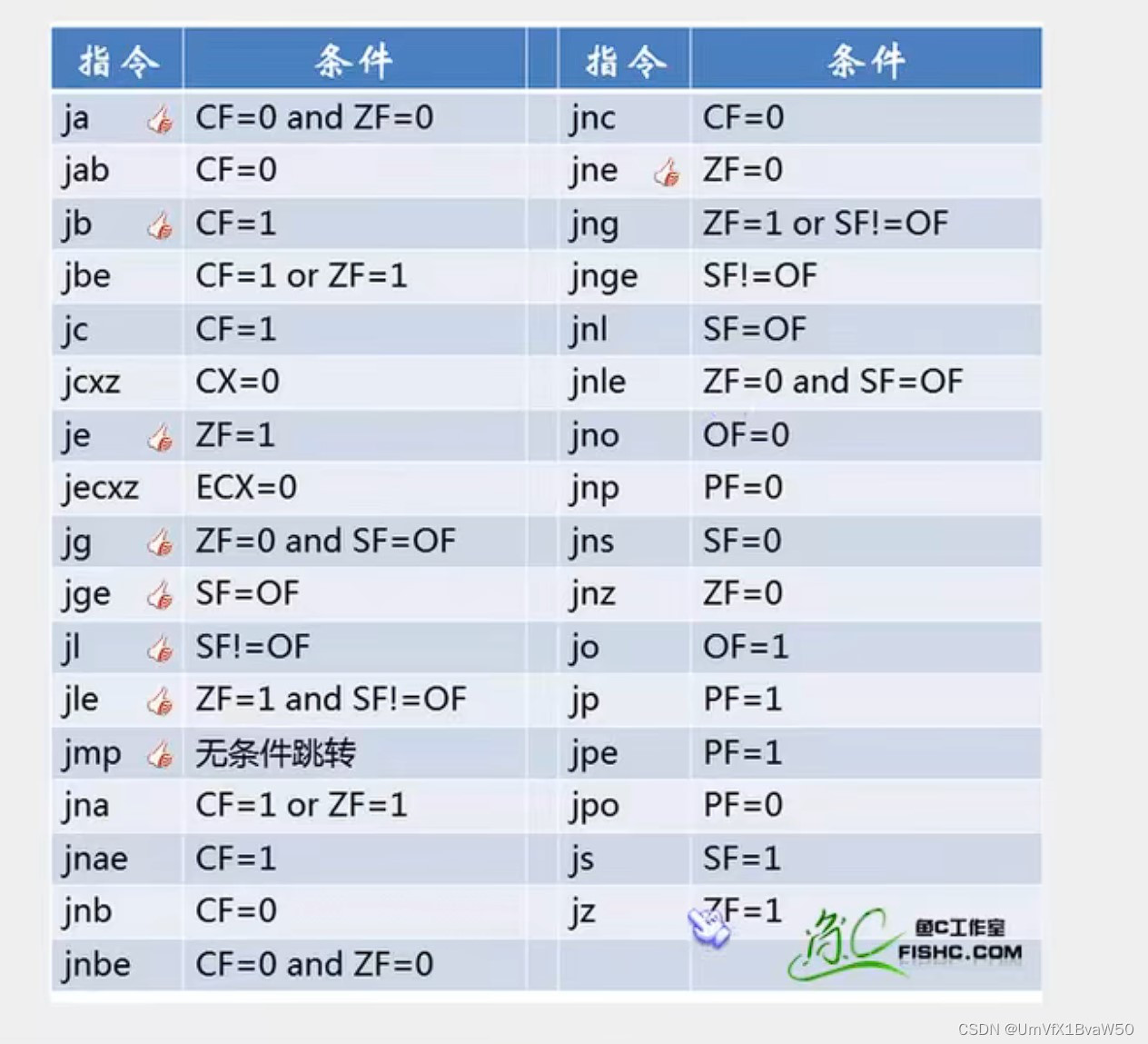
IDA常用操作、快捷键总结以及使用技巧
先贴一张官方的图,然后我再总结一下,用的频率比较高的会做一些简单标注 快捷键 F系列【主要是调试状态的处理】 F2 添加/删除断点F4 运行到光标所在位置F5 反汇编F7 单步步入F8 单步跳过F9 持续运行直到输入/断点/结束 shift系列【主要是调出对应的页…...

Kibana使用指南
使用介绍主要特点应用场景数据可视化还有哪些类型安装步骤安装配置参数Elasticsearch配置参数注意事项 使用介绍 Kibana是一个开源的分析与可视化平台,设计出来用于和Elasticsearch一起使用的。可以用Kibana搜索、查看、交互存放在Elasticsearch索引里的数据&#…...
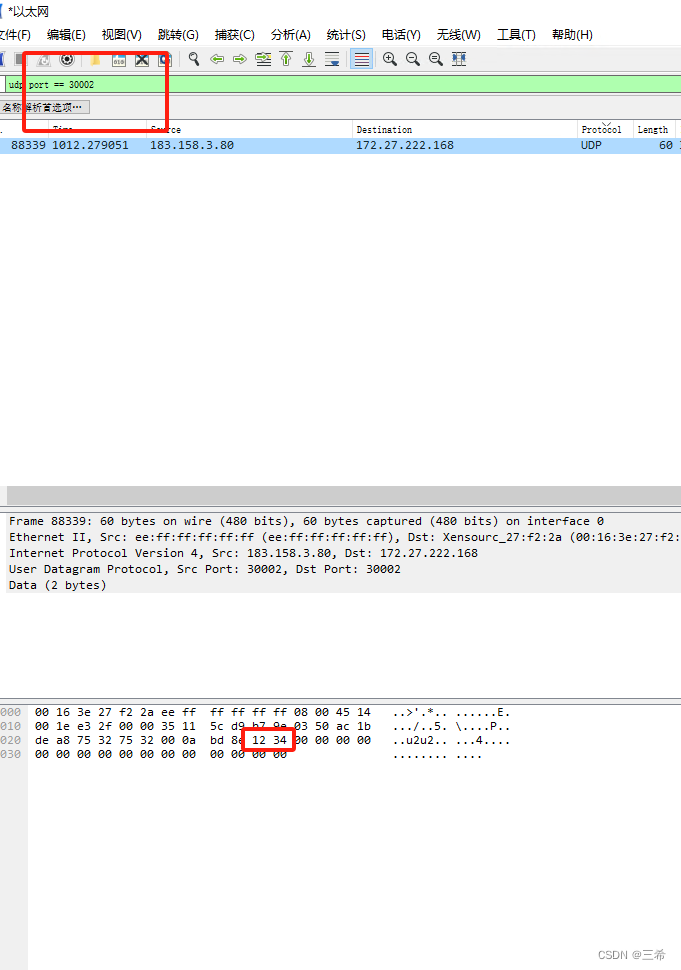
wvp如果确认音频udp端口开放成功
用到工具 在服务器上开启端口监听 选中udp server,点击创建按钮 设置服务器监听端口 在客户端连接服务器端口 选中udp客户端,点击创建 输入服务器地址 远程端口和本地端口,本地端口只要没被占用都可以使用 ,点击确认 发送数据 …...
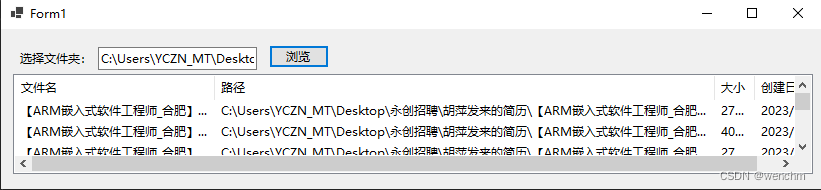
C#文件夹基本操作(判断文件夹是否存在、创建文件夹、移动文件夹、删除文件夹以及遍历文件夹中的文件)
目录 一、判断文件夹是否存在 1.Directory类的Exists()方法 2. DirectoryInfo类的Exists属性 二、创建文件夹 1. Directory类的CreateDirectory()方法 2.DirectoryInfo类的Create()方法 三、移动文件夹 1. Directory类的Move()方法 2.DirectoryInfo类的MoveT…...
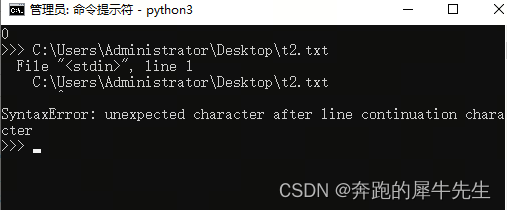
python 交互模式和命令行模式的问题
python 模式的冲突 unexpected character after line continuation character 理论上 ide里,输入 python 文件路径\文件.py 就可以执行 但是有时候却报错 unexpected character after line continuation character 出现上述错误的原因是没有退出解释器&#x…...
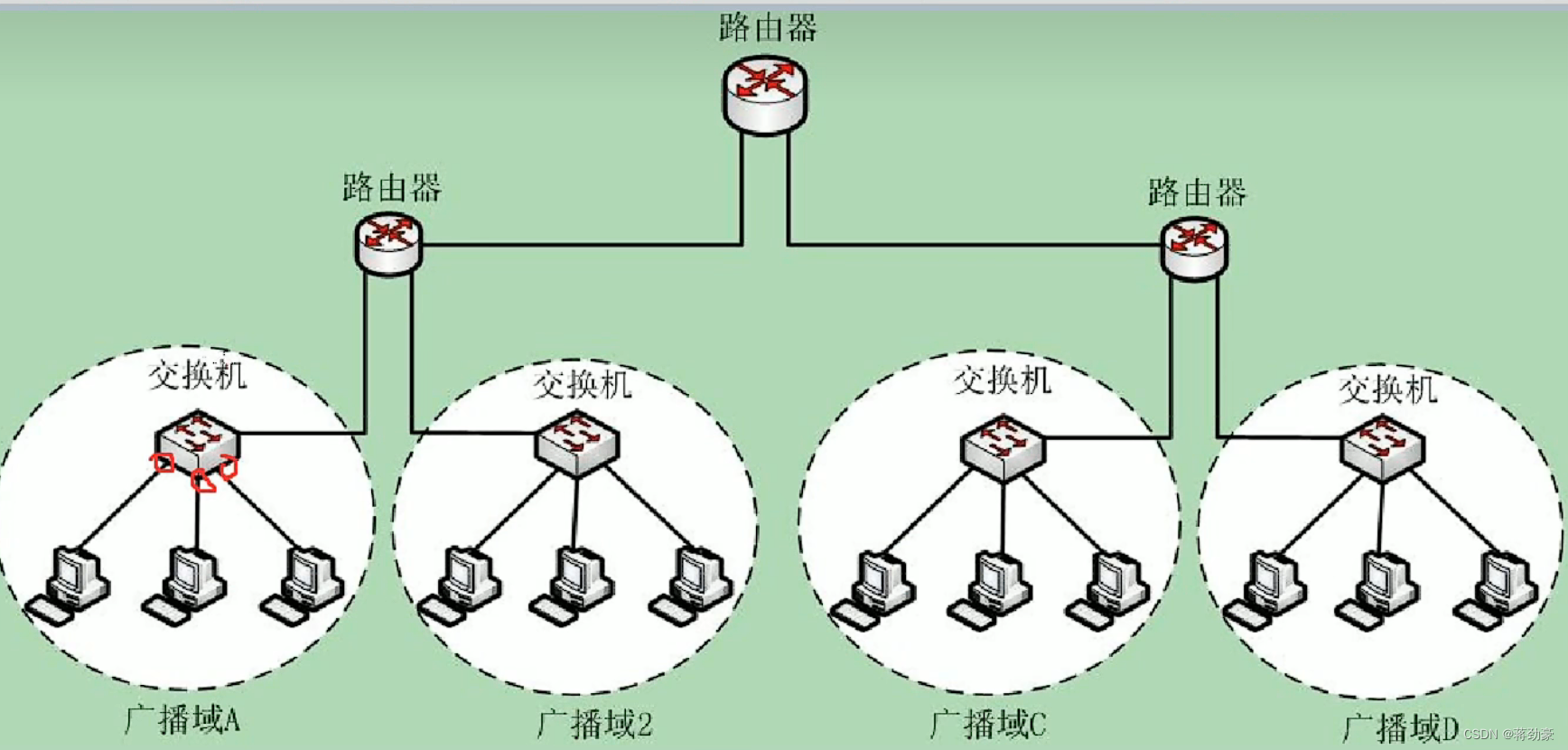
计算机网络——数据链路层
目录 一、数据链路层的基本概念 (一)数据链路层的概念 (二)帧 (三)数据链路层分为哪两个部分 (1)LLC(逻辑控制访问) (2)MAC&…...

【限时免费】20天拿下华为OD笔试之【哈希集合】2023B-明明的随机数【欧弟算法】全网注释最详细分类最全的华为OD真题题解
文章目录 题目描述与示例题目描述输入描述输出描述:示例 1输入输出说明 解题思路代码PythonJavaC时空复杂度 华为OD算法/大厂面试高频题算法练习冲刺训练 题目描述与示例 题目描述 明明生成了N 个 1 至 500 之间的随机整数。请你删去其中重复的数字,即…...
:视频帧处理并用SDL渲染播放)
播放器开发(五):视频帧处理并用SDL渲染播放
目录 学习课题:逐步构建开发播放器【QT5 FFmpeg6 SDL2】 步骤 VideoOutPut模块 1、初始化【分配缓存、读取信息】 2、开始线程工作【从队列读帧->缩放->发送渲染信号到窗口】 VideoWidget自定义Widget类 1、定义内部变量 2、如果使用SDL,需要进…...

Spring MVC数据绑定的几种方法(一)
这篇文章包含spring mvc的默认数据类型绑定和简单数据类型绑定。内容来自实验。 准备: (1)在IDEA环境中从archetye创建webapp类型的maven项目exp6。 (2)在src\main目录下创建并标注java源代码文件夹和resources资源文…...
)
CSP-坐标变换(其二)
问题描述 对于平面直角坐标系上的坐标 (x,y),小 P 定义了如下两种操作: 拉伸 k 倍:横坐标 x 变为 kx,纵坐标 y 变为 ky; 旋转 θ:将坐标 (x,y) 绕坐标原点 (0,0) 逆时针旋转 θ 弧度(0≤θ<…...

docker 安装jekins
echo Asia/Shanghai >/etc/timezone,容器中操作报错:docker容器中 Permission denied 使用该-u选项时,可以使用root用户(ID 0),而不是用默认用户登录docker容器 docker exec -u 0 -it f8a2b3d91455 /bin/bash 或者ÿ…...

ChatGPT 问世一周年之际,开源大模型能否迎头赶上?
就在11月30日,ChatGPT 迎来了它的问世一周年,这个来自 OpenAI 的强大AI在过去一年里取得了巨大的发展,迅速吸引各个领域的用户群体。 我们首先回忆一下 OpenAI和ChatGPT这一年的大事记(表格由ChatGPT辅助生成)&#x…...
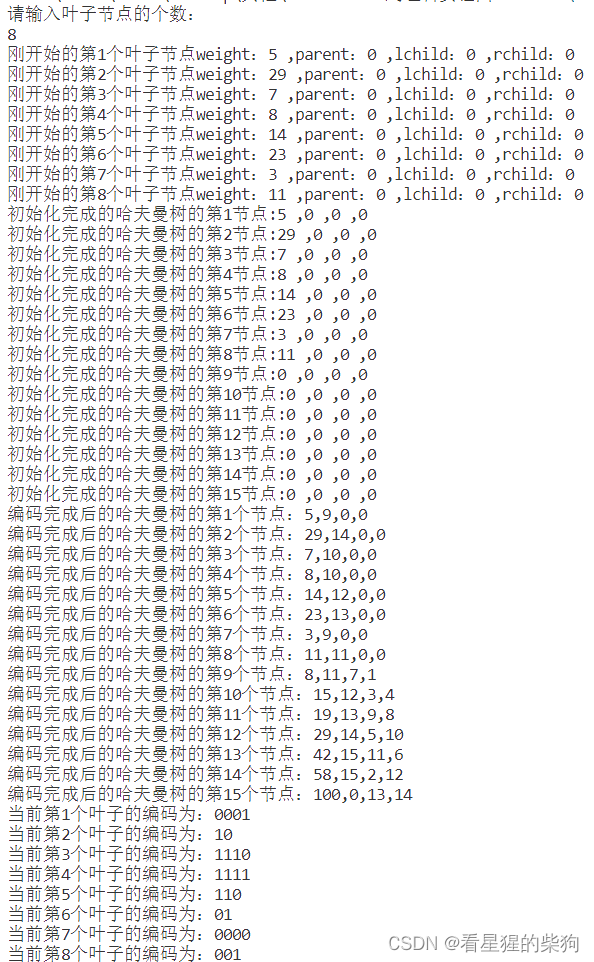
数据结构和算法-哈夫曼树以相关代码实现
文章目录 总览带权路径长度哈夫曼树的定义哈夫曼树的构造法1法2 哈夫曼编码英文字母频次总结实验内容: 哈夫曼树一、上机实验的问题和要求(需求分析):二、程序设计的基本思想,原理和算法描述:三、调试和运行…...

Kafka 的起源和背景
Apache Kafka 是一个分布式流处理平台,被广泛用于构建实时数据流应用程序和大数据处理系统。本文将深入探讨 Kafka 的起源、设计原则以及它在大数据领域中的重要作用。 大数据和实时数据处理背景 在大数据时代,处理海量数据和实时数据成为了一项关键挑…...
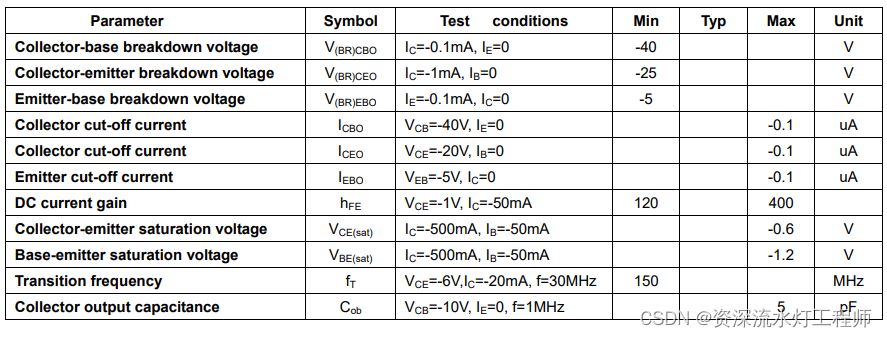
三极管在数字电路中的应用
一、认识三极管 三极管拥有3个引脚,分别对应3个级:基极(Base)、发射极(Emitter)、集电极(Collector),如下图所示;下图横向左侧的是基极,带箭头的那个引脚就是发射极,另一个就是集电…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
