数据结构与算法设计分析——NP完全理论
目录
- 一、P类问题与NP类问题的定义
- 二、常见的NP类问题
- (一)旅行商问题(TSP)
- (二)哈密尔顿回路问题
- (三)判断回路问题
- (四)图的着色问题
- (五)背包问题
- 三、P类问题和NP类问题的区别
- 四、NP完全问题
一、P类问题与NP类问题的定义
P类问题与NP类问题是计算机科学和数学中的两类重要问题,简单的来说,P类问题是较“容易”的问题,在计算机中,可以在多项式时间内解决,而NP类问题是较“复杂”的问题,它并不能在多项式时间内解决,只能验证是否存在解(解是否正确)。
常见的P类问题有排序、搜索算法等等,但不是所有的排序算法都是P类问题,例如,下表中快速排序、堆排序和归并排序是P类问题,其平均时间复杂度呈多项式,由于插入排序、冒泡排序、简单选择排序的平均时间复杂度都呈指数级,所以不属于P类问题,而是NP类问题。
| 排序名称 | 平均时间复杂度 |
|---|---|
| 直接插入排序 | O(n2) |
| 折半插入排序 | O(n2) |
| 希尔排序 | 依赖于增量序列 |
| 冒泡排序 | O(n2) |
| 快速排序 | O(nlog2n) |
| 简单选择排序 | O(n2) |
| 堆排序 | O(nlog2n) |
| 归并排序 | O(nlog2n) |
二、常见的NP类问题
(一)旅行商问题(TSP)
旅行商问题中给定一组城市和每对城市之间的距离,寻找一条最短路径,使得旅行者能够遍历所有城市并回到起始城市。
由于该问题的复杂度是指数级的,所以不存在多项式时间的确定性算法来解决它,属于NP类问题。
(二)哈密尔顿回路问题
对于一个有向图,判断是否存在一条回路可以经过图中所有顶点且不重复的问题,称为哈密尔顿回路问题。
在遍历图中的顶点时,需要经过所有可能的路径从而判断,且需要遍历的路径呈指数级增加,所以该问题也是个NP类问题。
(三)判断回路问题
同样,对于一个图,若要判断图中是否有回路,可以通过深度优先搜索(DFS)和广度优先搜索(BFS)来判断,两种搜索算法都会遍及图中所有的结点,所以该问题也是个NP类问题。
(四)图的着色问题
给定一个无向图和若干种颜色,给图中的每个顶点着色,使得任意相邻的两个顶点颜色不同,即为图的着色问题。
若针对一个顶点涂色,则其邻边的顶点与该顶点颜色均不同,从而一直进行下去,该图中所有的颜色组合数呈指数级增加,可以采用贪心算法和回溯算法来解决,所以该问题也是个NP类问题。
(五)背包问题
给定一组物品,每个物品都有自己的重量和价值,背包的容量有限,求如何选择物品放入背包,使得背包内的物品总价值最大,即为背包问题。
同样,物品的选择和组合方式的数量随着物品数量的增加而呈指数级增长,所以该问题也是个NP类问题。
三、P类问题和NP类问题的区别
P类问题和NP类问题的区别在于时间复杂度,P类问题可以在多项式时间内的确定性算法来进行判定或求解问题,且一般P类问题的求解较简单,时间复杂度较低,而NP类问题可以在多项式时间内的不确定性算法来进行判定或求解问题,其求解过程较困难,但一般都是去验证问题。
四、NP完全问题
NP完全问题是NP问题的一个子类,可以说它是更复杂的问题,也是在多项式时间内验证问题的解。例如多项式变换技术问题、布尔可满足性问题以及上面的旅行商问题(TSP)、哈密尔顿回路问题等等。
相关文章:

数据结构与算法设计分析——NP完全理论
目录 一、P类问题与NP类问题的定义二、常见的NP类问题(一)旅行商问题(TSP)(二)哈密尔顿回路问题(三)判断回路问题(四)图的着色问题(五)…...
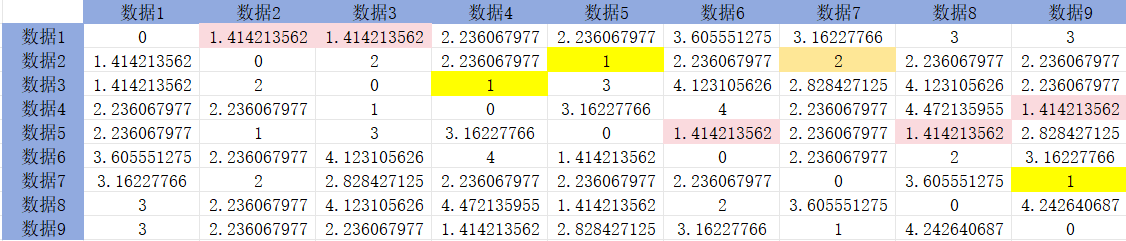
AGNES层次聚类
已知数据集D中有9个数据点,分别是(1,2),(2,3),(2,1), (3,1),(2,4),(3,5),(4,3),(1,5),(4,2)。要求: (1)采用层次聚类的聚集算法进行聚类,k2。 (2)距离计算采用欧几里得距离。 (3)簇之间的距离采用单链接方…...
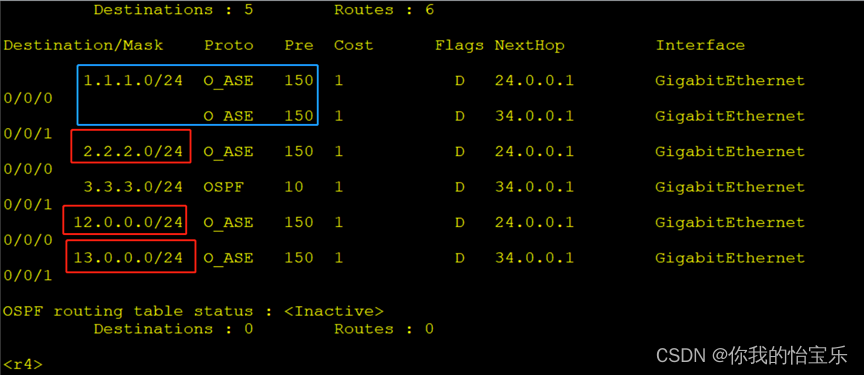
HCIP —— 双点重发布 + 路由策略 实验
目录 实验拓扑: 实验要求: 实验配置: 1.配置IP地址 2.配置动态路由协议 —— RIP 、 OSPF R1 RIP R4 OSPF R2 配置RIP、OSPF 双向重发布 R3配置RIP、OSPF 双向重发布 3.查询路由表学习情况 4.使用路由策略控制选路 R2 R3 5.检…...

Python标准库:datetime模块【侯小啾python领航班系列(二十五)】
Python标准库:datetime模块【侯小啾python领航班系列(二十五)】 大家好,我是博主侯小啾, 🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ…...
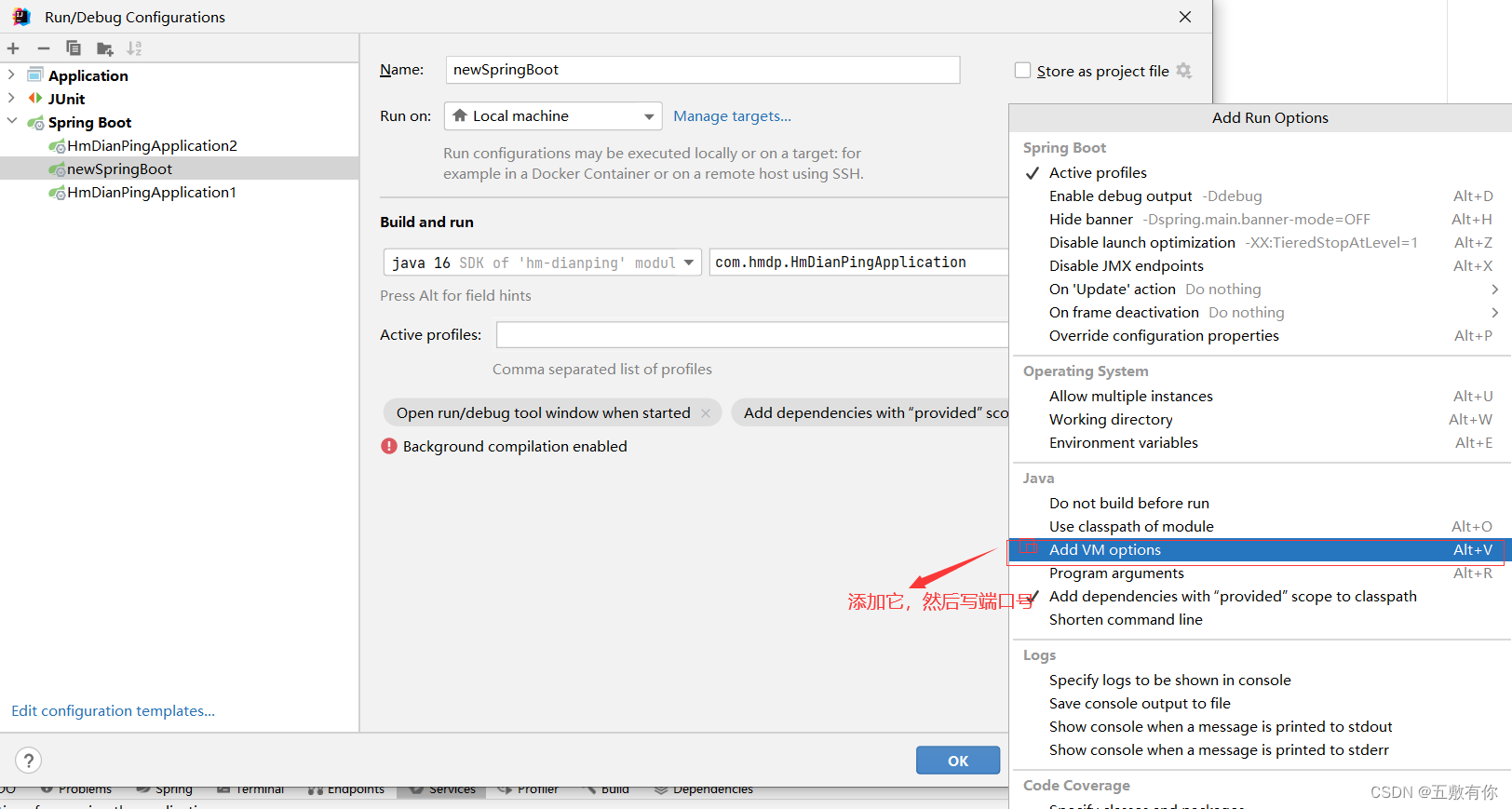
新版idea如何开启多台JVM虚拟机
1.看看自己的项目 2.可能开始的时候啥也没有,就点Run Configuration Type 3.再点击Edit Configurations... 4.点击号添加SpringBoot 5.主类选择一下,一般就一个,点他选了就行。 6.然后点击Modify Options 选择添加add VM Options 7.点击appl…...

软件工程单选多选补充
2. 4. 5. 6. 7. 8. 9. 10. 12。 13....
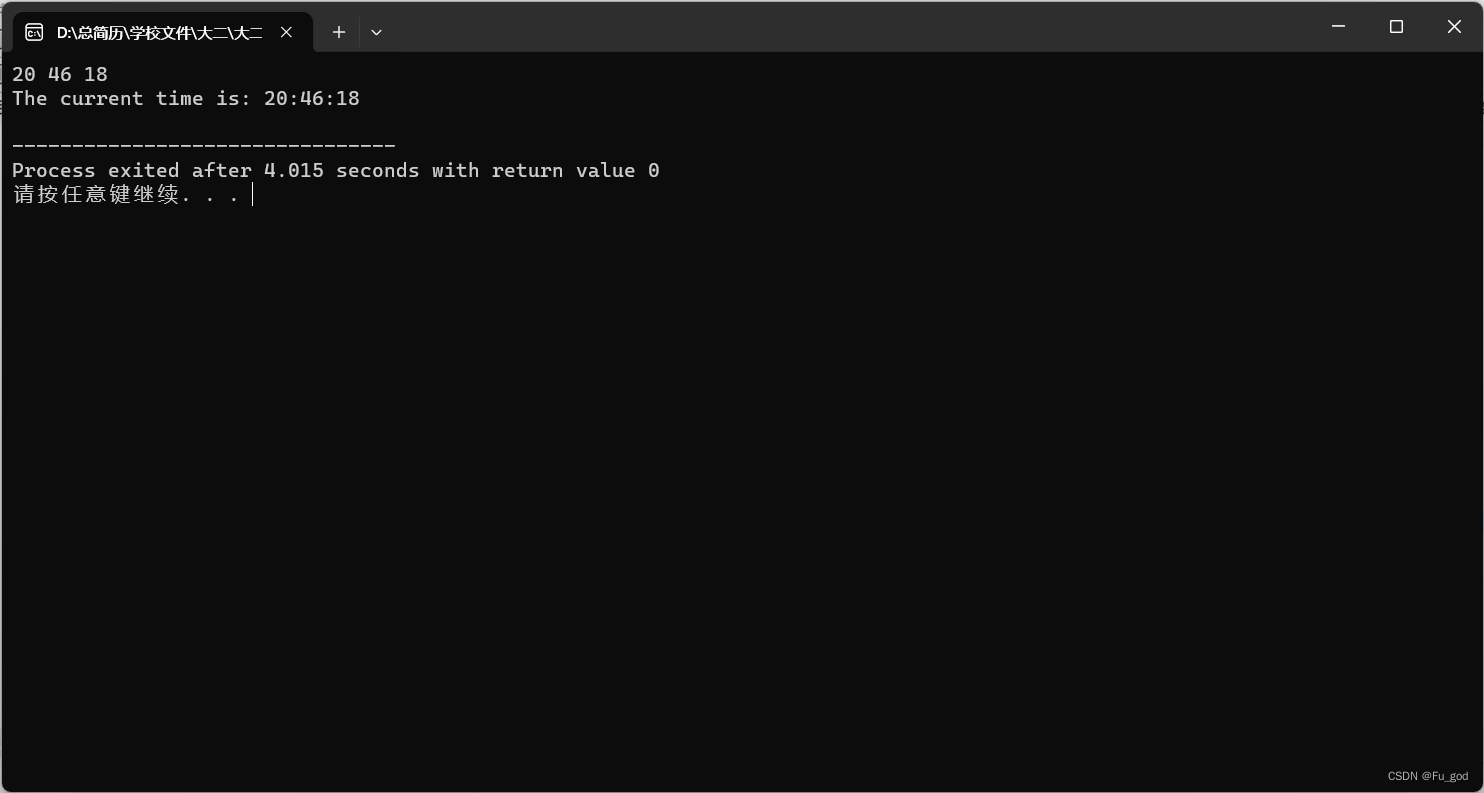
6-66.时间
本题要求输入小时、分钟和秒数,并将其输出。针对时间表示中出现的异常进行处理。例如小时数不应超过23,分钟不应超过59,秒数不应超过59。此外,以上三个变量均应大于等于0。 输入样例: 在这里给出三组输入。例如&…...
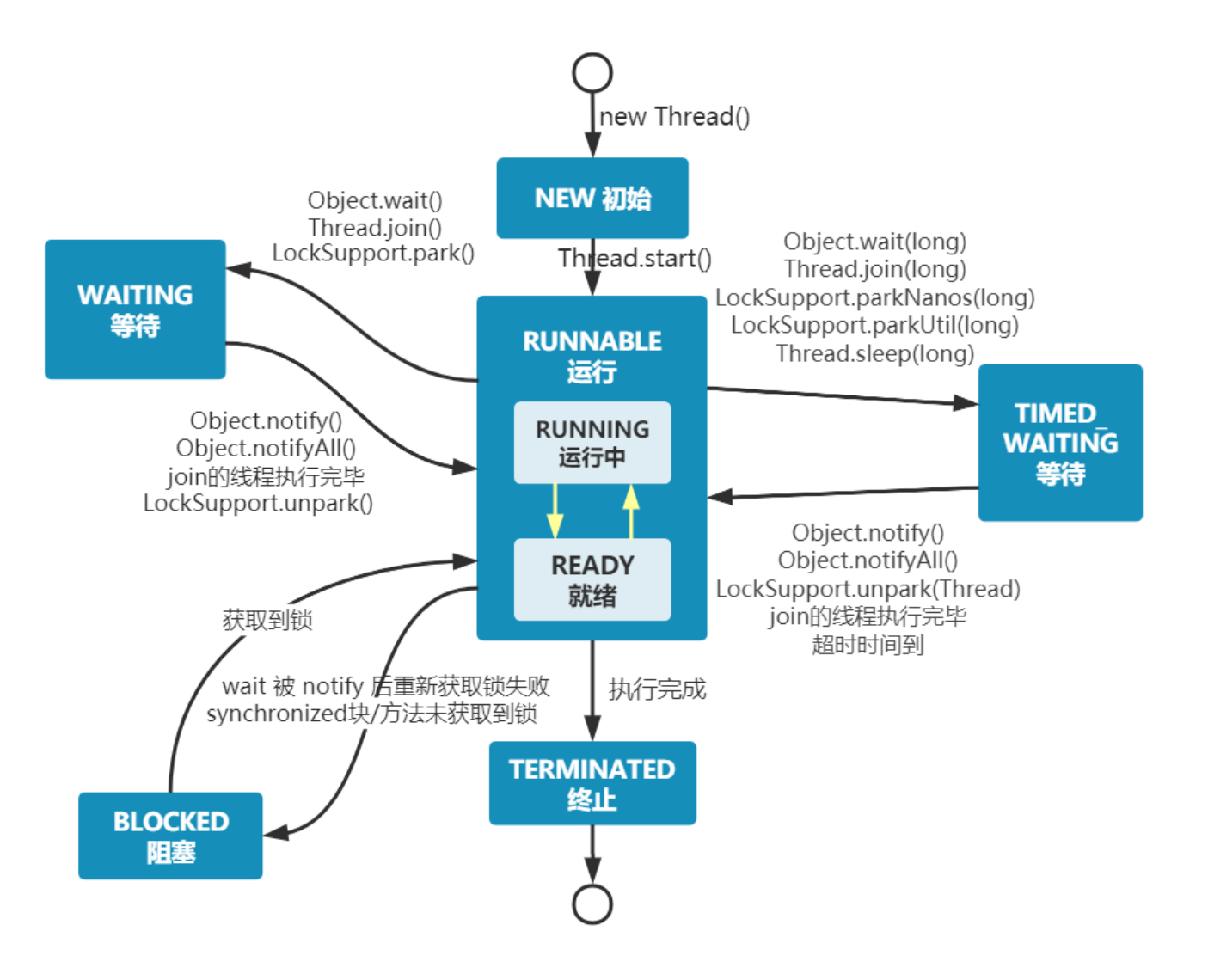
面试多线程八股文十问十答第一期
面试多线程八股文十问十答第一期 作者:程序员小白条,个人博客 相信看了本文后,对你的面试是有一定帮助的! ⭐点赞⭐收藏⭐不迷路!⭐ 1.ThreadLocal如何实现线程安全 Java的ThreadLocal是一个线程本地变量࿰…...
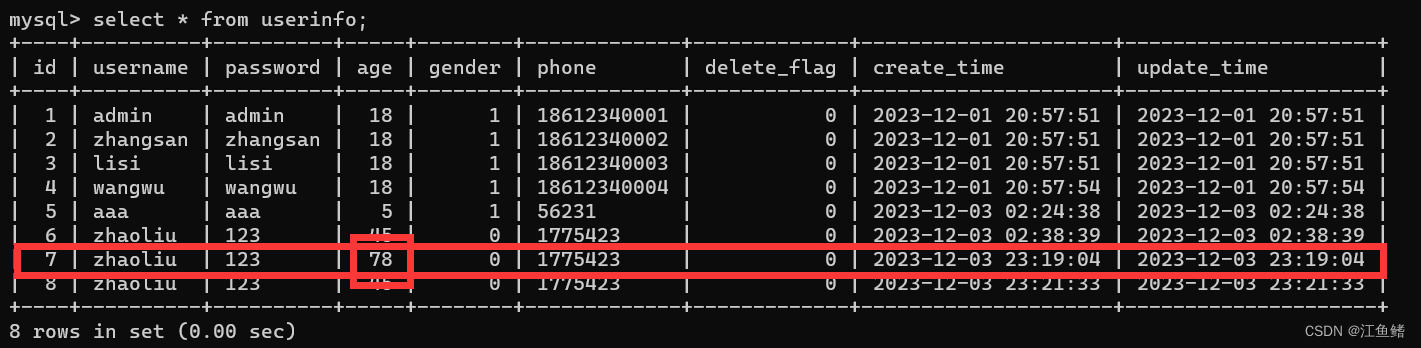
Mybatis 操作续集(结合上文)
当我们增加一个数据之后,如果我们想要获取它的 Id 进行别的操作,我们该如何获取 Id 呢? 用那个Options package com.example.mybatisdemo.mapper;import com.example.mybatisdemo.model.UserInfo; import org.apache.ibatis.annotations.*;import java.util.List;Mapper pub…...
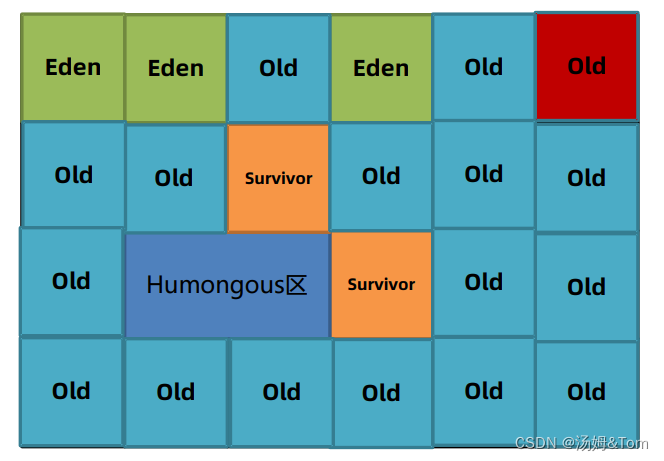
JVM基础篇:垃圾回收
目录 1.前言 1.1C/C的内存管理 1.2Java的内存管理 2.方法区的回收 3.堆回收 3.1引用计数法和可达性分析法 3.2五种对象引用 强引用 软引用 弱引用 虚引用 终结器引用 3.3垃圾回收算法评价标准 ①吞吐量 ②最大暂停时间 ③堆使用效率 3.4垃圾回收算法 ①标记清…...

蓝桥杯ACwing习题
题目 :https://www.acwing.com/problem/content/4409/ 解析 :根据题目我们可以知道 问的是方案数 那么首先就想到了 dp 仔细想一下 发现类似于蒙德里安的梦想那道状态压缩的题 , 所以我们先考虑怎么定义 f[i][j] f[i][j] 表示的是 已经放了…...
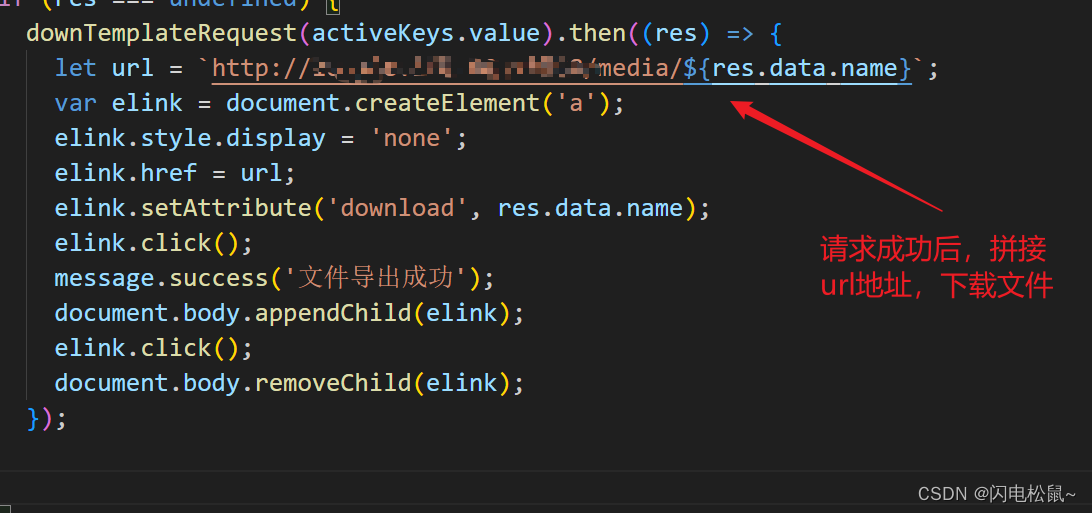
vue发送请求携带token,拼接url地址下载文件
封装请求 ,该请求为普通的get请求 该请求返回值为: 请求成功之后拼接URL地址下载文件 代码块 downTemplateRequest(activeKeys.value).then((res) > {let url http://47.169.168.99:18888/media/${res.data.name};var elink document.createElemen…...

【PTA-C语言】编程练习3 - 循环结构Ⅱ
如果代码存在问题,麻烦大家指正 ~ ~有帮助麻烦点个赞 ~ ~ 编程练习3 - 循环结构(9~15) 7-9 特殊a串数列求和(分数 15)7-10 穷举法搬运砖块问题(分数 15)7-11 数字金字塔(分数 15&…...
Google Chrome 下载 (离线版)
1 访问网址 Google Chrome 网络浏览器 2 点击 下载Chrome 3 直接运行 ChromeStandaloneSetup64.exe 其他: ####################### 谷歌浏览器 (Google Chrome) 最新版离线安装包下载 https://www.iplaysoft.com/tools/chrome/#google_vignette Google Chrome …...

2023年GopherChina大会-核心PPT资料下载
一、峰会简介 自 Go 语言诞生以来,中国便是其应用最早和最广的国家之一,根据 Jetbrains 在 2021 年初做的调查报告,总体来说目前大概有 110 万专业的开发者 选择 Go 作为其主要开发语言。就其全球分布而言, 居住在亚洲的开发者最多ÿ…...

从源代码出发,Jenkins 任务排队时间过长问题的解决过程
最近开发了一个部署相关的工具,使用 Jenkins 来构建应用。Jenkins 的任务从模板中创建而来。每次部署时,通过 Jenkins API 来触发构建任务。在线上运行时发现,通过 API 触发的 Jenkins 任务总是会时不时在队列中等待较长的时间。某些情况下的…...

openssl 生成CA及相关证书
实验环境:ubuntu18.04-desktop 获取openssl.cnf配置文件 # 这个返回的路径,不一定被使用了(经测试,ubuntu18下的openssl似乎未加载任何配置文件) openssl version -d生成私钥文件(pem) # 生成私钥 # genrsa…...

App测试之App日志收集及adb常用命令
文章目录 前言一、adb是什么1.APP测试收集手机日志常用的工具2.adb下载与安装3.ADT/SDK/ADB是什么4.adb连接真机 二、adb常用命令三、android系统日志文件1.logcat日志文件2.logcat日志文件分析 四、分析crash & ANR 日志1.发生crash如何分析2.发生ANR如何分析 总结扩展&am…...

【Java面试——并发基础、并发关键字】
3.1 并发基础 Java 并发 - 理论基础Java 并发 - 线程基础 多线程的出现是要解决什么问题的? 本质什么? CPU、内存、I/O 设备的速度是有极大差异的,为了合理利用 CPU 的高性能,平衡这三者的速度差异,计算机体系结构、操作系统、编译程序都…...
如何使用 Java 在Excel中创建下拉列表
下拉列表(下拉框)可以确保用户仅从预先给定的选项中进行选择,这样不仅能减少数据输入错误,还能节省时间提高效率。在MS Excel中,我们可以通过 “数据验证” 提供的选项来创建下拉列表,但如果要在Java程序中…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
