贪心 55. 跳跃游戏 45.跳跃游戏 II

55. 跳跃游戏

题目：

给定非负数组，初始位置在数组第一格，数组值是可以选择的最大跳跃步数，判断能不能达到数组末尾。

示例  1:
* 输入: [2,3,1,1,4]
* 输出: true
* 解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。

示例  2:
* 输入: [3,2,1,0,4]
* 输出: false
* 解释: 无论怎样，你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 ， 所以你永远不可能到达最后一个位置。

贪心思路：

局部：求每一步的最大覆盖范围，记录下来，有更大的范围更新
全局：当遍历完，最大覆盖范围的i大于等于末尾的i，判断可以，否则不行。

如下图过程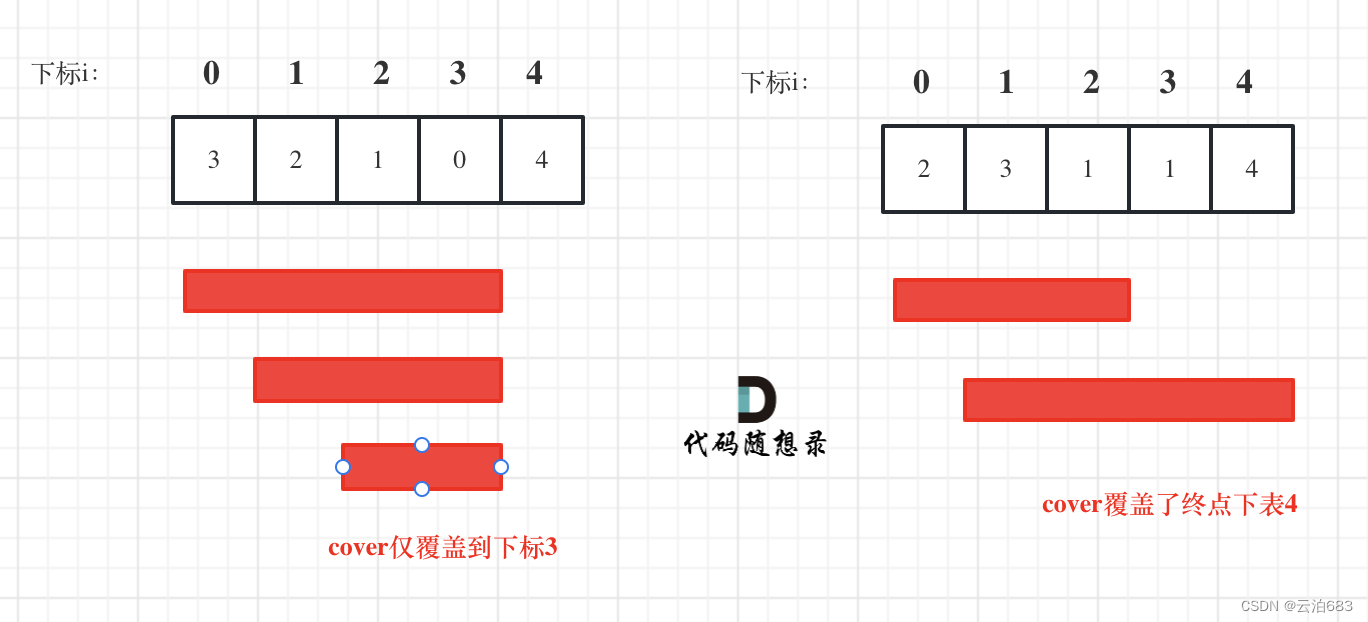

 代码如下：  

class Solution {
public:bool canJump(vector<int>& nums) {int cover = 0;if (nums.size() == 1) return true; // 只有一个元素，就是能达到for (int i = 0; i <= cover; i++) { // 注意这里是小于等于covercover = max(i + nums[i], cover);if (cover >= nums.size() - 1) return true; // 说明可以覆盖到终点了}return false;}
};

45.跳跃游戏 II

题目

给定一个非负整数数组，你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置，然后返回最少的步数

（这里默认可以走到末尾）

示例1:
* 输入: [2,3,1,1,4]
* 输出: 2
* 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置，跳  1  步，然后      跳  3  步到达数组的最后一个位置。

贪心思路：

局部最优：当前可移动距离尽可能多走，如果还没到终点，步数再加一。

全局最优：一步尽可能多走，从而达到最少步数。

从覆盖范围出发，不管怎么跳，覆盖范围内一定是可以跳到的，以最小的步数增加覆盖范围，覆盖范围一旦覆盖了终点，得到的就是最少步数！

这里需要统计两个覆盖范围，当前这一步的最大覆盖和下一步最大覆盖。

如果移动下标达到了当前这一步的最大覆盖最远距离了，还没有到终点的话，那么就必须再走一步来增加覆盖范围，直到覆盖范围覆盖了终点。

求出遍历下标的最大覆盖范围内所有下标可以走的最大距离，比如从下标0开始，如果下标的范围不能覆盖末尾，那么遍历下标0覆盖范围的所有下标，比如下标1，下标2，看看当下一步走到下标1和下标3的时候，可不可以让整体的跳跃覆盖范围到末尾，如果这样覆盖范围到末尾了，比如下图1，它的值是3覆盖到末尾了，那么说明这里就是最短路径。

如果范围内的下标的可覆盖范围都没到末尾，说明要前进一步继续寻找。比如下图如果到了下标2如果还没找到就需要前进一步，i++了。

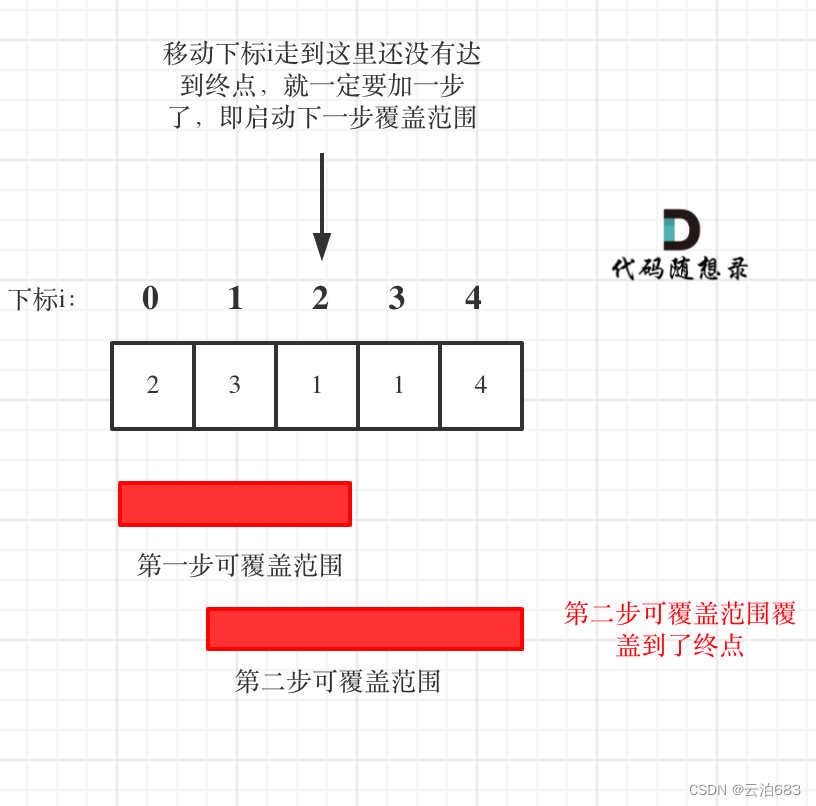
代码如下：

// 版本一
class Solution {
public:int jump(vector<int>& nums) {if (nums.size() == 1) return 0;int curDistance = 0;    // 当前覆盖范围最远距离下标（当前步数最远边界）int ans = 0;            // 记录走的最大步数int nextDistance = 0;   // 下一步的最大覆盖范围for (int i = 0; i < nums.size(); i++) {// 当前最大跳跃覆盖范围 和 之前的下一步最大覆盖距离 对比来 更新 这个时候的下一步最大覆盖距离nextDistance = max(nums[i] + i, nextDistance);// 更新下一步的最大覆盖范围，if (i == curDistance) {                   // 遇到当前覆盖最远距离下标  （这个一开始，0=0会运行一次，可参考上面图片）ans++;                                  // 需要走下一步curDistance = nextDistance;             // 更新当前覆盖最远距离下标（相当于加油了）if (nextDistance >= nums.size() - 1) break;  // 当前覆盖最远距到达集合终点，不用做ans++操作了，直接结束}}return ans;}
};

 疑问1：

nextDistance = max(nums[i] + i, nextDistance) 这段代码什么意思？

nums[i] + i表示从当前位置 i 在单次跳跃中可以到达的最远范围。而nextDistance 表示在之前的遍历过程中可达的最远范围，确保nextDistance始终是下一步最大的可达范围。