研习代码 day47 | 动态规划——子序列问题3
一、判断子序列
1.1 题目
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
进阶:
如果有大量输入的 S,称作 S1, S2, ... , Sk 其中 k >= 10亿,你需要依次检查它们是否为 T 的子序列。在这种情况下,你会怎样改变代码?
示例 1:
输入:s = "abc", t = "ahbgdc" 输出:true
示例 2:
输入:s = "axc", t = "ahbgdc" 输出:false
提示:
0 <= s.length <= 1000 <= t.length <= 10^4- 两个字符串都只由小写字符组成。
1.2 题目链接
392.判断子序列
1.3 解题思路和过程想法
(1)解题思路
双指针遍历:用两个指针分别遍历两个字符串,若是两指针所指相同,则两指针同时往后;否则,将指向“母字符串”的指针向后移动;最后判断指向“子字符串”的指针是否到达其串后侧位置
动态规划:用两层循环结构对比两字符串的元素,外层遍历“子串”,内层遍历“母串”。若是两指针所指的前一元素相同——s[i-1] == t[j-1],则更新“以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度dp[i][j]” ——dp[i][j] = dp[i-1][j-1]+1;若是二者不相等,则dp[i][j]等于前值,不做更新——dp[i][j] = dp[i][j-1];最后判断dp[len(s)][len(t)]==lens(s)即可。
(2)过程想法
一题多解才能融会贯通所学的知识
1.4 代码
1.4.1 双指针遍历
class Solution:def isSubsequence(self, s: str, t: str) -> bool:# 利用双指针分别指向两个字符串point_s , point_t = 0, 0# 遍历字符串 t while point_s < len(s) and point_t < len(t):# 若匹配,则两指针都向后移一位if s[point_s] == t[point_t]:point_s += 1# 否则,只有指针 t 向后移point_t += 1# 若指针 s 到达最后,则表明匹配成功return point_s == len(s)1.4.2 动态规划
class Solution:def isSubsequence(self, s: str, t: str) -> bool:m,n = len(s),len(t)dp = [[0] * (n+1) for _ in range(m+1)]for i in range(1, m+1):for j in range(1, n+1):if s[i-1] == t[j-1]:dp[i][j] = dp[i-1][j-1] + 1else:dp[i][j] = dp[i][j-1]if dp[m][n] == m:return Trueelse:return False二、不同的子序列
1.1 题目
给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 109 + 7 取模。
示例 1:
输入:s = "rabbbit", t = "rabbit" 输出:3 解释: 如下所示, 有 3 种可以从 s 中得到 "rabbit" 的方案。rabbbitrabbbitrabbbit
示例 2:
输入:s = "babgbag", t = "bag" 输出:5 解释: 如下所示, 有 5 种可以从 s 中得到 "bag" 的方案。babgbagbabgbagbabgbagbabgbagbabgbag
提示:
1 <= s.length, t.length <= 1000s和t由英文字母组成
1.2 题目链接
115.不同的子序列
1.3 解题思路和过程想法
(1)解题思路
当前的匹配情况会受到之前元素的情况所影响,且影响的方式是类似的,考虑采用动态规划的策略。数组:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]
递推关系:若二者元素相匹配,当前情况取决于 用或不用 当前的元素,
dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
若二者元素不匹配,当前情况的结果与不用当前元素的情况相同
dp[i][j] = dp[i-1][j]

图片来源:代码随想录,红色文字是自己加的
初始化:由上述递推关系可知当前位置的填写是基于左上方和正上方的元素,所以需要提前对首行首列进行初始赋值
# 首行:没有母串,直接赋值 0
dp[0][j] = 0
# 首列:没有子串,即空子串,赋值1
dp[i][0] = 1
(2)过程想法
递推关系的式子着实是没想到,,,
1.4 代码
class Solution:def numDistinct(self, s: str, t: str) -> int:long,short = len(s),len(t)# 以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]# 以母串位置为行坐标,以子串位置为列坐标dp = [[0]*(short+1) for _ in range(long+1)]# 递推关系:若二者元素相匹配,当前情况取决于 用或不用 当前的元素# 若匹配,则dp[i][j] = dp[i-1][j-1] + dp[i-1][j]# 初始化:由上述递推关系可知当前位置的填写是基于左上方和正上方的元素,所以需要提前对首行首列进行初始赋值for j in range(short+1): # 首行:没有母串,直接赋值 0dp[0][j] = 0for i in range(long+1): # 首列:没有子串,即空子串,赋值1dp[i][0] = 1for i in range(1,long+1):for j in range(1,short+1):if s[i-1] == t[j-1]:dp[i][j] = dp[i-1][j-1] + dp[i-1][j]else:dp[i][j] = dp[i-1][j]return dp[long][short]相关文章:

研习代码 day47 | 动态规划——子序列问题3
一、判断子序列 1.1 题目 给定字符串 s 和 t ,判断 s 是否为 t 的子序列。 字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde&…...

L1-017:到底有多二
题目描述 一个整数“犯二的程度”定义为该数字中包含2的个数与其位数的比值。如果这个数是负数,则程度增加0.5倍;如果还是个偶数,则再增加1倍。例如数字-13142223336是个11位数,其中有3个2,并且是负数,也是…...
)
Python多线程使用(二)
使用多个线程的时候容易遇到一个场景:多个线程处理一份数据 使用多线程的时候同时处理一份数据,在threading中提供了一个方法:线程锁 Demo:下订单 现在有多笔订单下单,库存减少 from threading import Thread from t…...

记录一次docker搭建tomcat容器的网页不能访问的问题
tomcat Tomcat是Apache软件基金会的Jakarta项目中的一个重要子项目,是一个Web服务器,也是Java应用服务器,是开源免费的软件。它是一个兼容Java Servlet和JavaServer Pages(JSP)的Web服务器,可以作为独立的W…...

GPT3年终总结
User You 程序员年度绩效总结 ChatGPT ChatGPT 程序员年度绩效总结通常包括以下几个方面: 目标达成情况: 回顾年初设定的目标,评估在项目完成、技能提升等方面的达成情况。 工作贡献: 强调在项目中的个人贡献,包括…...

Kafka生产者发送消息的流程
Kafka 生产者发送消息的流程涉及多个步骤,从消息的创建到成功存储在 Kafka 集群中。以下是 Kafka 生产者发送消息的主要步骤: 1. 创建消息 生产者首先创建一个消息,消息通常包含一个键(可选)和一个值,以及…...
基于SSM的数学竞赛网站设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:Vue 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目:是 目录…...

01-使用Git操作本地库,如初始化本地库,提交工作区文件到暂存区和本地库,查看版本信息,版本切换命令等
Git的使用 概述 Git是一个分布式版本控制工具, 通常用来管理项目中的源代码文件(Java类、xml文件、html页面等)进行管理,在软件开发过程中被广泛使用 Git可以记录文件修改的历史记录并形成备份从而实现代码回溯, 版本切换, 多人协作, 远程备份的功能Git具有廉价的本地库,方便…...
排序算法介绍(二)冒泡排序
0. 简介 冒泡排序(Bubble Sort)是一种简单的排序算法。它重复地遍历要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排…...

搜索引擎高级用法总结: 谷歌、百度、必应
搜索引擎高级用法总结: 谷歌、百度、必应 google search 基本搜索 逻辑与:and逻辑或: or逻辑非: -完整匹配:“关键词”通配符:* ?高级搜索 intext:后台登录 将只返回正文中包含 后台登录 的网页 intitle intitle:后台登录 将只返回标题中包含 后台登录 的网页,intitle…...

com.intellij.openapi.application.ApplicationListener使用
一般监听期通过如下代码生效 <applicationListeners> <!-- <listener class"com.itheima.taunt.MyApplicationListener"--> <!-- topic"com.intellij.openapi.application.ApplicationListener"…...

常见js hook脚本
一.js hook 过无限debugger var _constructor constructor; Function.prototype.constructor function(s) {if (s "debugger") {console.log(s);return null;}return _constructor(s); }//去除无限debugger Function.prototype.__constructor_back Function.pro…...

Java——SpringLayout弹簧布局
import java.awt.*;import javax.swing.*;public class a {public static void main(String[] args) {new a();}public a() {JFrame JF new JFrame("弹簧布局");// 创建JFrame窗口//设置JPanel的布局管理器为SpringLayoutJPanel JP new JPanel(new SpringLayout())…...
正则表达式及文本三剑客grep sed awk
目录 正则表达式 1.元字符 2.表示次数 3.位置锚定 4.分组或其他 grep sed 语法: 常用选项 脚本格式 例: 查找11点56到12点10的日志 修改文件,找到文件并给其后缀加上er 提取IP地址 提取版本号 提取文件权限 awk 工作原理&…...

python爬虫之创建属于自己的ip代理池
在后续需求数据量比较大的情况下,自建一个ip代理池可以帮助我们获得更多的数据。 下面我来介绍一下整个过程 1.找到目标代理网站 https://www.dailiservers.com/go/webshare https://proxyscrape.com/ https://spys.one/ https://free-proxy-list.net/ http://fr…...

又添三位“信伙伴”,亚信安慧AntDB数据库与南京一鸣、广东鸿数、北京数见完成兼容互认
近日,亚信安慧AntDB数据库与南京一鸣科技有限公司(简称:南京一鸣)学生工作管理与服务平台软件、广东鸿数科技有限公司(简称:广东鸿数)隐私数据保护系统V5.0、北京数见科技有限公司(简…...
Linux --- 进程控制
目录 1. 进程创建 1.1. 内核数据结构的处理 1.2. 代码的处理 1.3. 数据的处理: 方案一:fork创建子进程的时候,直接对数据进行拷贝处理,让父子进程各自私有一份 方案二:写实拷贝(copy on write) 1.4. fork常规用…...

SVG-椭圆弧-参数转换-计算公式-标准解读
文章目录 1.简介2.基本参数2.1.椭圆的表达2.2.参数变换2.3.注意事项 3.参考资料4.总结 1.简介 为了与其他路径段表示法保持一致, SVG 路径中的圆弧是根据曲线上的起点和终点定义的。椭圆弧的这种端点参数化。优点是它允许与其它路径一致的语法,其中所有…...

利用 LD_PRELOAD劫持动态链接库,绕过 disable_function
目录 LD_PRELOAD 简介 程序的链接 动态链接库的搜索路径搜索的先后顺序: 利用LD_PRELOAD 简单的劫持 执行id命令 反弹shell 引申至 PHP 绕过disable_function 方法1:使用蚁剑的扩展工具绕过disable_function 方法2:利用 mail 函数…...
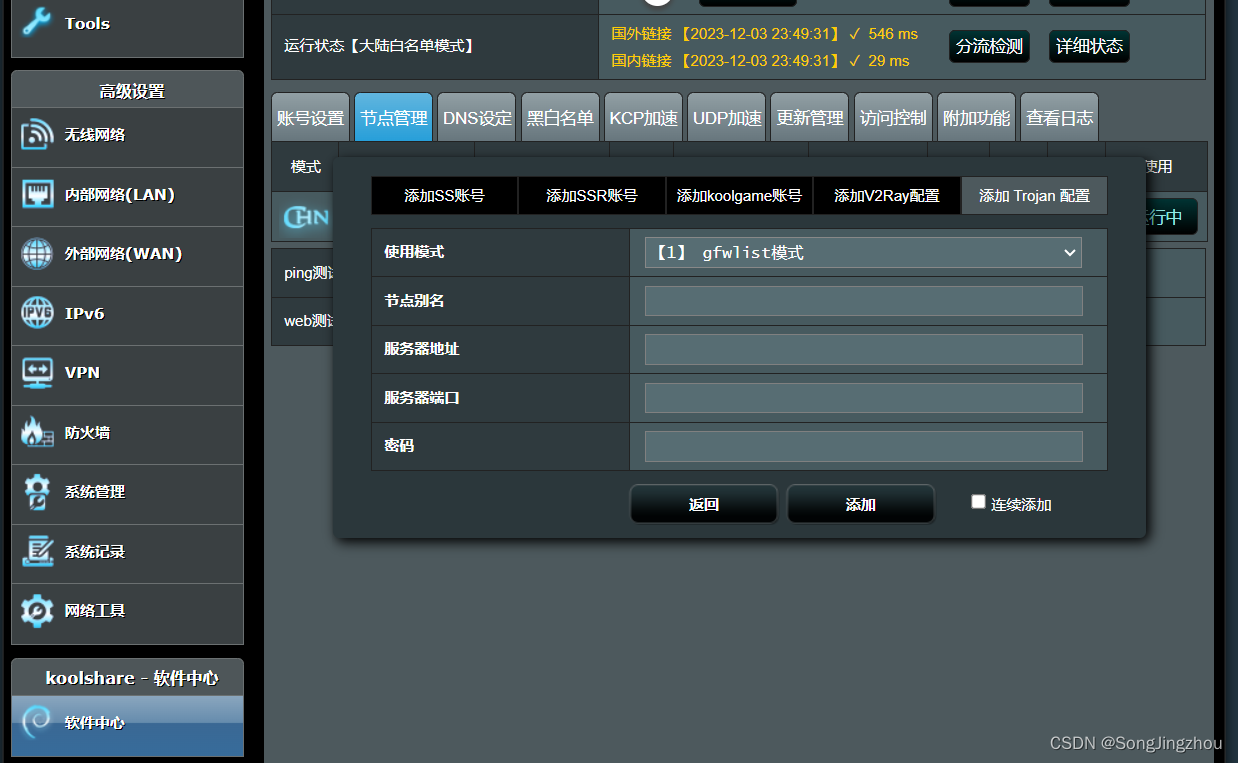
网件R8500 trojan
一 将路由器刷机成改版梅林 路由器首页的Firmware:380.70_0-X7.9.1是梅林改版 380.xx 梅林原版固件 380.xx_x 梅林改版固件 必须是改版梅林才支持trojan,所以要确保是梅林改版固件 点击上传文件,选择下载好的改版固件,固件地址下载传送门…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...
