当前位置： 首页 > news >正文

C++ 红黑树的封装

news 2025/7/7 14:08:34

一.map/set的封装

  在实现了红黑树的部分功能后，我们可以便可以将红黑树作为底层结构来封装map 和 set ，但是问题也随之而来。我们都知道map是k-v的数据模型，而set是k的数据模型，我们难道要去使用两棵红黑树来封装吗？显然不是这样的。

  接下来我们将使用同一棵红黑树实现 map和set。

1.1 封装的基本思路 

  因为我们是用一棵红黑树去封装两种容器，使用我们的这棵红黑树，使用我们的这棵树就不能像以前一样写死成k-v模型的数据结构，需要稍作修改。

  因为红黑树不能自己判断其是否是map/set类型，我们能做的努力就是提高其适应性，对红黑树的要求为：

    既能适配 K-V模型的map，又能适配出K 模型的set。 

对map和set的要求为：

    需要准确的传入数据，传入时让红黑树只能适配出一个类型的容器，对不需要的部分进行切割。

1.2 红黑树节点的调整

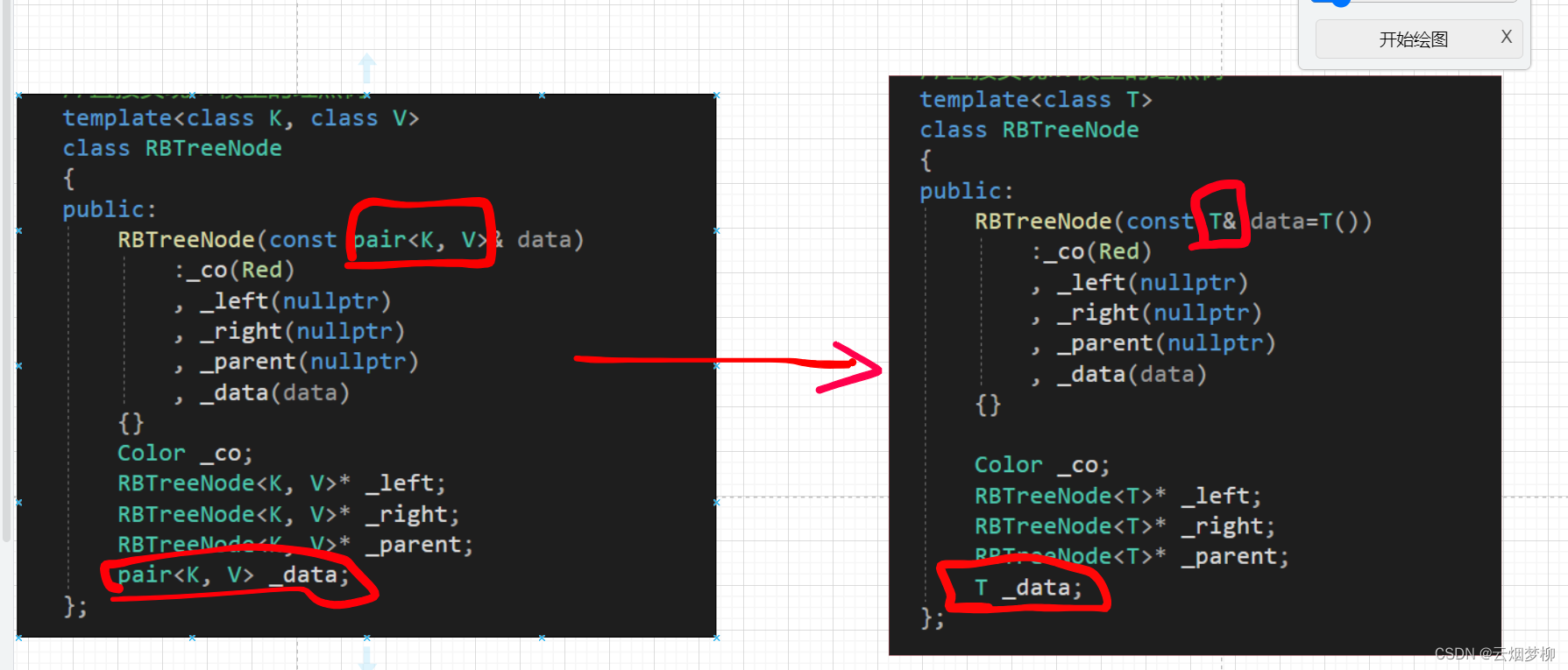
  这是我们之前写出的红黑树节点，现在来看显然不太合适，因为我们已经把K-V模型写死了，不太好适配出K模型的set。

  在这里，我们建议让pair类型变成 一个模糊的 T类型，至于是pair 类型还是 k类型，我们希望让map和set来准确的传入。

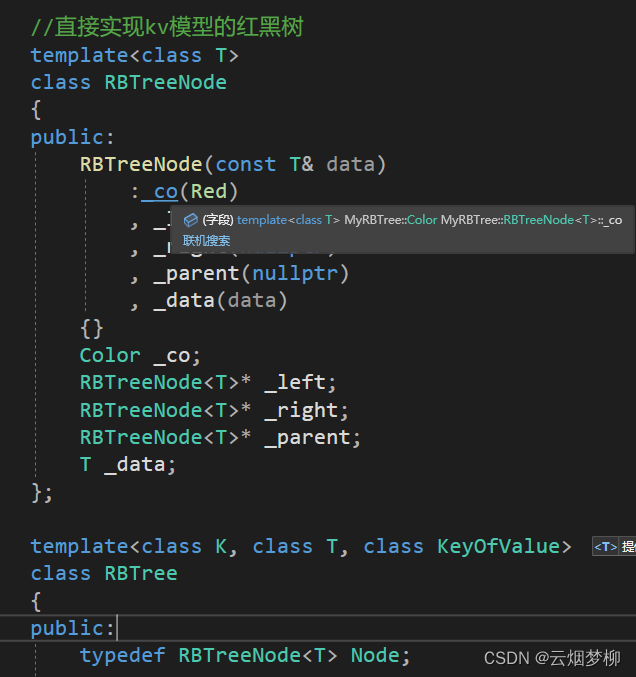
1.3 map 和 set 的定义 

  我们该如何适配map和set的底层，来让其匹配红黑树呢？

  在这里，我建议让其内部的模板，暂时先有两个数据类型，第一个为 K 模型，第二个为 T模型，也就是说 当为map时，传入map<K,K>时，底层实际传入RBTree<k,pair<k,k>>,传入set<k>时，底层实际传入RBTree<K,K>。

  这样有什么好处呢？ 

   为因为我们的底层实现是红黑树，那么我们为了适应map又适应set，实际传入的代表数据参数至少得是两个，可能会有些人问：“map可以直接传入pair啊，那么为什么不直接传入一个RBTree<pair<K,V>>呢？。

  因为有find的存在，map的find是按照k来进行查找的，如果直接传入pair类型，那么红黑树里面的实际类型只有一个pair，当我们查找时，根本无法按照key类型来查找，所以我们的红黑树至少得有两个模板参数。

  因此，即使set是k模型，但是在这里的底层结构上，我们仍然需要传入两个k类型。

map和set基本定义如下：
 

#pragma once
#include"RBTree.h"using namespace MyRBTree;namespace MySet
{template<class K>class Set{private:RBTree<K, K> _set;};
} 
#pragma once
#include"RBTree.h"using namespace MyRBTree;namespace MyMap
{template<class K,class V>class Map{private:RBTree<K, pair<K,V>> _map;};
}

1.4 仿函数 KeyOfValue

  在insert中，我们经常会用到data进行一些比较，但是我们现在data的类型不固定，如果是map中的pair类型，我们就应该用其first进行比较，如果是k类型，我们就应该直接比较。

  最好的解决办法是，在map和set内部分别定义一个KetOfValue 仿函数，然后将其传入红黑树模板中，因为其传入的内容不同，所以我们用来分别处理不同的数据。

  如果是map中的data，因为是kv结构，所以我们取出其data.first;如果是set中的k模型，那么我们直接返回，仿函数定义如下：
  

#pragma once
#include"RBTree.h"
using namespace MyRBTree;namespace MyMap
{template<class K,class V>class Map{public:struct MapKeyOfvalue{const K& operator()(const pair<K, V>& kv){return kv.first;}};private:RBTree<K, pair<K,V>, MapKeyOfvalue> _map;};
}
#pragma once
#include"RBTree.h"using namespace MyRBTree;namespace MySet
{template<class K>class Set{public:struct SetKeyOfvalue{const K& operator()(const K& key){return key;}};private:RBTree<K, K, SetKeyOfvalue> _set;};
}

同时我们因为要多传入一个仿函数，所以我们的模板和map，set内部的红黑树模板参数也要进行修改：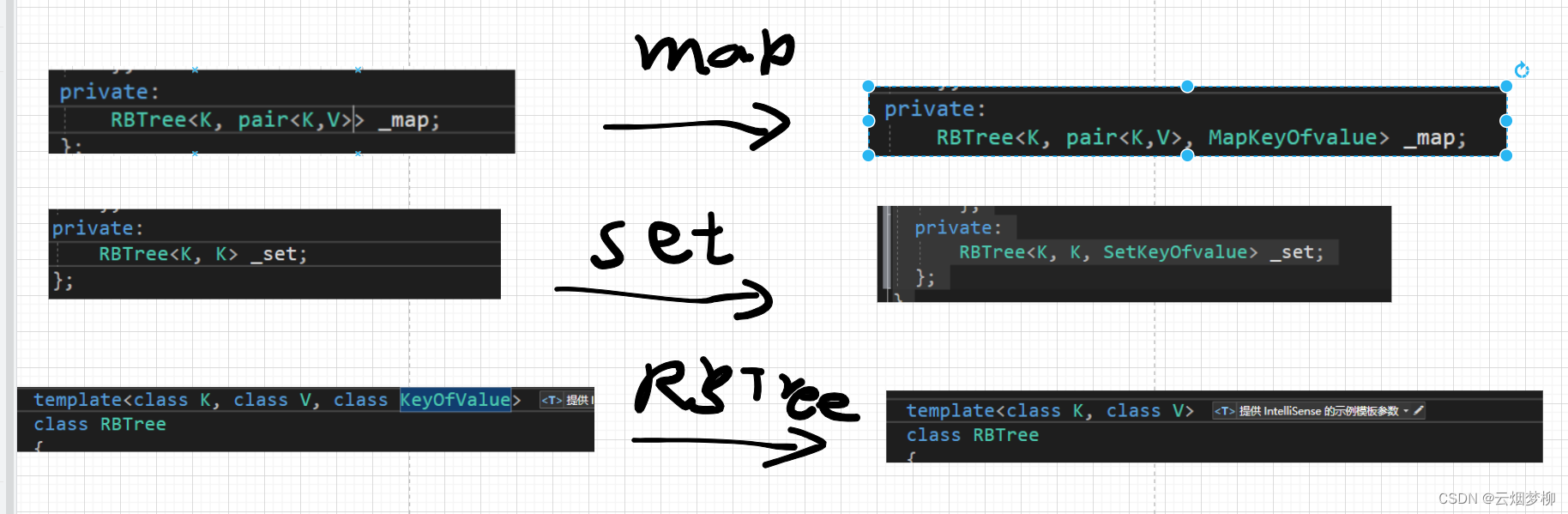

同时，我们在红黑树内部也需要对进行数据比对的函数进行修改，比如说insert和find等等。

	bool Insert(const pair<K, V>& data){//因为需要使用仿函数的机会不多，我们在需要用到的地方局部创建一下就可以了//如何大多数函数都需要用到，建议定义为全局变量KeyOfValue kot;if (!_root){_root = new Node(data);_root->_co = Black;return true;}Node* cur = _root;Node* parent = nullptr;while (cur){//if (cur->_data.first < data.first)if (kot(cur->_data)< kot(data)){parent = cur;cur = cur->_right;}//else if (cur->_data.first > data.first)else if (kot(cur->_data) > kot(data.first)){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(data);cur->_co = Red;//if (parent->_data.first < cur->_data.first)if (kot(parent->_data) < kot(cur->_data)){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//开始判断是否需要变色while (parent && parent->_co == Red){Node* grand = parent->_parent;if (parent == grand->_left){Node* uncle = grand->_right;if (uncle && uncle->_co == Red){//这里只变色就好parent->_co = uncle->_co = Black;grand->_co = Red;cur = grand;parent = cur->_parent;}else{if (cur == parent->_left){_RotateR(grand);grand->_co = Red;parent->_co = Black;}else{_RotateL(parent);_RotateR(grand);cur->_co = Black;grand->_co = Red;}break;}}else{Node* uncle = grand->_left;if (uncle && uncle->_co == Red){//这里只变色就好parent->_co = uncle->_co = Black;grand->_co = Red;cur = grand;parent = cur->_parent;}else{if (cur == parent->_right){_RotateL(grand);grand->_co = Red;parent->_co = Black;}else{_RotateR(parent);_RotateL(grand);cur->_co = Black;grand->_co = Red;}break;}}}_root->_co = Black;return true;}
	Node* Find(const K& key){KeyOfValue kot;Node* cur = _root;while (cur){//if (cur->_data.first < key)if (kot(cur->_data) < key){cur = cur->_right;}//else if (cur->_data.first > key)else if (kot(cur->_data) > key){cur = cur->_left;}else{return cur;}}return nullptr;}

1.5 map/set的插入

  现在，在其内部直接套用红黑树的插入即可。

namespace MySet
{template<class K>class Set{public:struct SetKeyOfvalue{const K& operator()(const K& key){return key;}};bool insert(const K& k){return _set.Insert(k);}private:RBTree<K, K, SetKeyOfvalue> _set;};
} 
namespace MyMap
{template<class K,class V>class Map{public:struct MapKeyOfvalue{const K& operator()(const pair<K, V>& kv){return kv.first;}};bool insert(const pair<K,V> &kv){return _map.Insert(kv);}private:RBTree<K, pair<K,V>, MapKeyOfvalue> _map;};
}

 在map和set中先插入一些数据来看一下有没有更改错误：

这里建议在map和set内部封装进去红黑树的Inorder打印一下检查一下错误。

void Inorder()
{_map.Inorder();
}//判断一下是否平衡void IsBalance()
{_map.IsBalance();
}

同时我们的Inorder函数也需要更改

void _Inorder(Node* root)
{if (!root){return;}//这里我们也要更改一下_Inorder(root->_left);//cout << root->_data.first << ":" << endl;cout <<kot(root->_data) <<" ";_Inorder(root->_right);
}

验证一下map和set的准确性：

#include"MyMap.h"
#include"MySet.h"void testmap()
{MyMap::Map<int, int> _m;_m.insert(make_pair(1, 1));_m.insert(make_pair(2, 1));_m.insert(make_pair(3, 1));_m.insert(make_pair(4, 1));_m.insert(make_pair(5, 1));_m.Inorder();_m.IsBalance();cout << endl << endl;
}void testset()
{MySet::Set<int> _s;_s.insert(1);_s.insert(2);_s.insert(3);_s.insert(4);_s.insert(5);_s.Inorder();_s.IsBalance();cout << endl<<endl;
}int main()
{testmap();testset();return 0;
}

结果为：

二. map和set迭代器的实现 

  首先，我们要明白，map/set只是相当于一层壳子，真正的底层实现永远都在红黑树的部分，迭代器也是同理，我们撰写的迭代器应该书写在红黑树部分。

  迭代器的基本定义：

	//	   节点数据	 引用/const引用  指针/const指针template <class T, class Ref, class Ptr>struct _RBTreeIterator{typedef RBTreeNode<T> Node;typedef _RBTreeIterator<T, Ref, Ptr> self;Node* _node;_RBTreeIterator(Node* node):_node(node){}};

2.1 解引用运算符重载

  一般用来取出其节点中存储的数据，直接返回data即可，并且一般而言是是可以修改的，因此这里我们返回其引用。

Ref operator*()
{return _node->_data;
}

2.2 成员访问运算符重载

  -> 运算符一般用来返回该节点的地址，主要还是适用于map中，用来访问pair里面的first和second成员。

Ptr operator->()
{return &(_node->_data);
}

2.3 ==  和 != 运算符重载

这个就比较简单了

	bool operator==(const self& s){return _node == s._node;}bool operator!=(const self& s){return _node != s._node;}

 2.4 begin()和end()

  迭代器常用成员函数begin()与end()，其中begin()对应红黑树的最左节点，end()对应最后一个节点的下一个节点，即nullptr(这里我们并没有设置哨兵位，感兴趣的同学可以自己研究一下）

 
iterator begin()
{Node* left = _root;while (left && left->_left){left = left->_left;}return iterator(left);
}iterator end()
{return iterator(nullptr);
}

2.6 ++ 运算符重载

  首先我们要知道，红黑树也是一个二叉搜索树，我们对其的遍历顺序也是按照中序遍历，因此，++运算符在这里指的是，中序遍历的下一个节点。

  那我们该如何找寻中序遍历的下一个节点呢。

  我们先来观察一部分红黑树的遍历情况：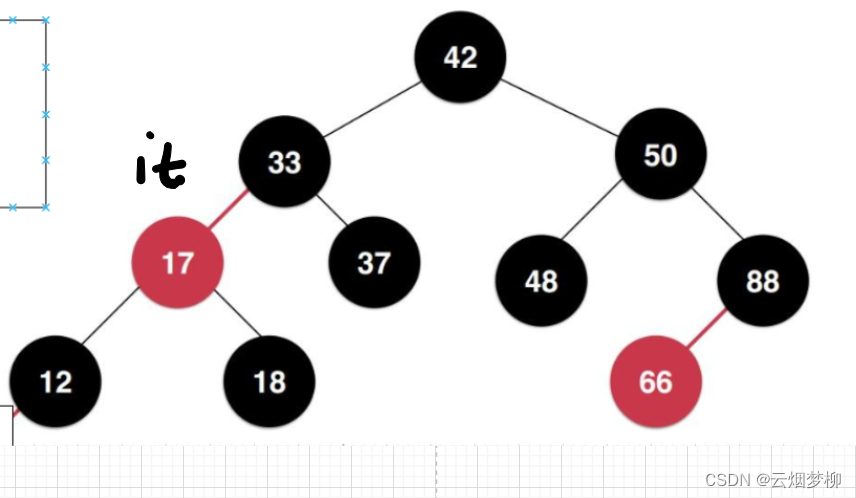

当it指向17 时，++实际上是去访问18这个节点；（17有右子树）

当it访问18时，++实际上是去访问33这个节点；（18无右子树，故向上遍历）

当it访问33时，++实际上是去访问37这个节点；（33有右子树）

当it访问37时，++实际上是去访问42这个节点；（37无右子树，向上遍历）

 我们可以看出，实际上++始终围绕着右子树进行移动：

1.当所在节点有右子树时，++访问右子树的最左节点

2.当所在节点没有右子树时，++ 找孩子不是父亲右节点的祖先（这里需要进行遍历）

故得到代码：
 

self& operator++() //迭代器++，依旧返回迭代器
{//如果右子树存在if (_node->_right){Node* left = _node->_right;//则寻找右子树的最左节点while (left->_left){left = left->_left;}_node = left;}//如果右子树不存在else{//找孩子不是父亲右节点的节点Node* parent = _node->_parent;Node* cur = _node; //一定要先判断parent是否存在，以此来避免越界while (parent&&cur == parent->_right){cur = cur->_parent;parent = parent->_parent;}_node = parent;}return *this;
}
//迭代器后置++self operator++(int){self it(_node);++(*this);return it;}

 2.7 --运算符重载

  --就是++ 代码思路反过来。

  1. 左子树不为空，进行 -- 则是指向左子树(最右节点)。
  2. 左子树为空，-- 找孩子不是父亲左节点的祖先（循环查找）

得到代码如下：

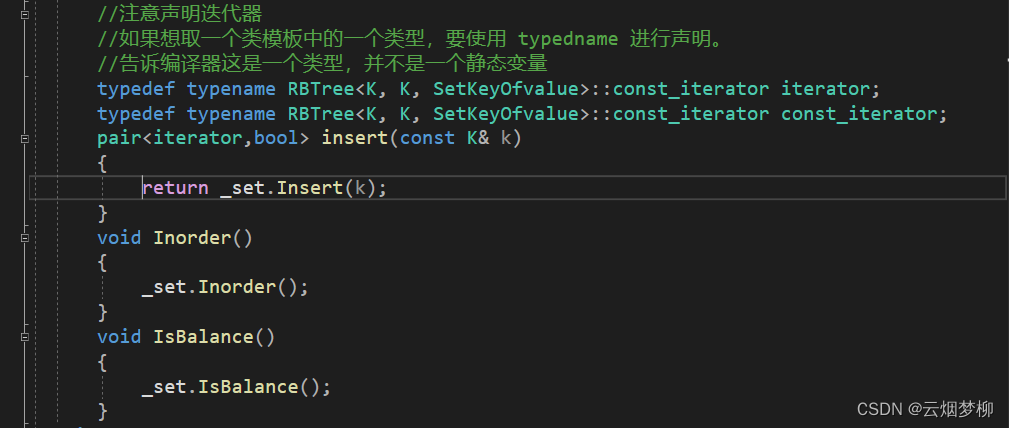
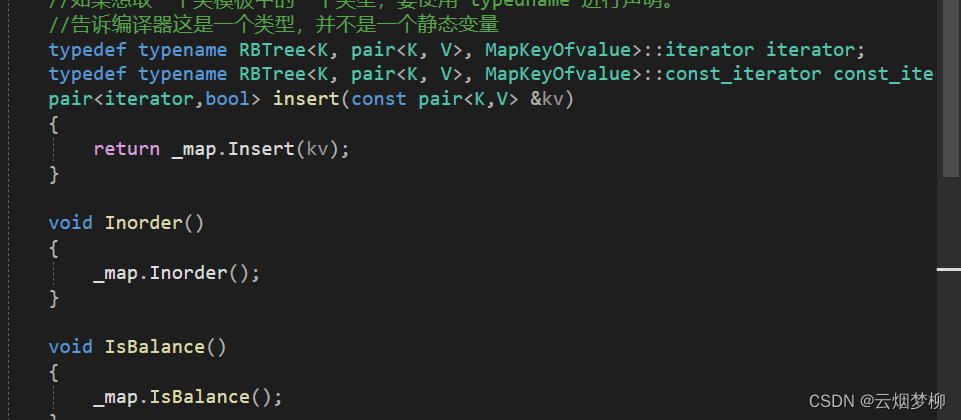
	self& operator--(){//如果左子树存在if (_node->left){//找左子树的最右节点Node* right = _node->_left;while (right->_right){right = right->_right;}_node = rihgt;}//如果左子树不存在else{//找孩子不是父亲左节点的节点Node* parent = _node->parent;Node* cur = _node;while (parent&&parent->_left == cur){cur = cur->_parent;parent = parent->_parent;}_node = parent;}return *this;}//后置--self operator--(int){self it(_node);--(*this);return it;}

迭代器在map和set中的封装如下：


 

三 map的[] 下标访问运算符重载

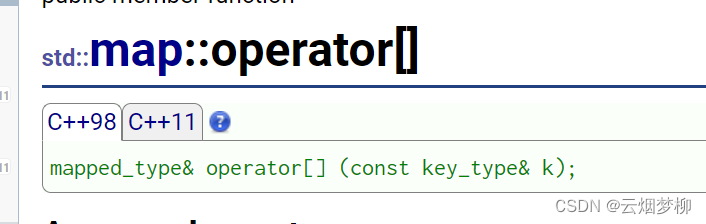
我们可以看到其返回为，mapped_type类型，这是什么呢？

map文档中有如下声明：
 

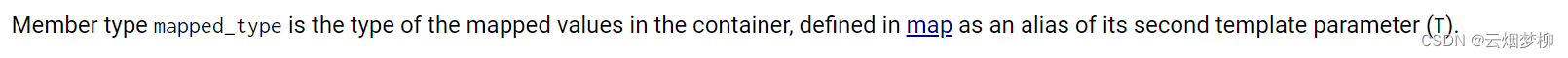
翻译一下我们得知，在map中定义为其第二个模板参数T，（我们这里为V）的别名

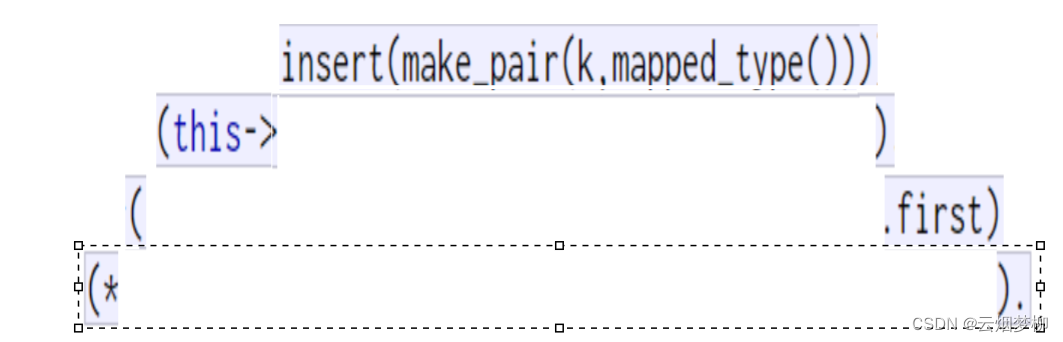
在官方库里面，对这个【】是这样实现的：

 太迷茫了，我们拆解来看一下：

里面的第一层为：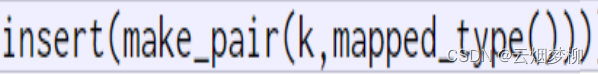

  可见就是一层简单的插入 ，第一个传入的是k的值，第二个是我们map中第二个模板参数V的默认构造。

 第二步，将this指针指向insert返回的这个内容。

第三步， 取出this指向的内容中的first内容，那么问题来了，我们自己定义的insert返回的内容是bool类型，我们该取这个的first吗，显然不是的，让我们看看库中的insert函数。

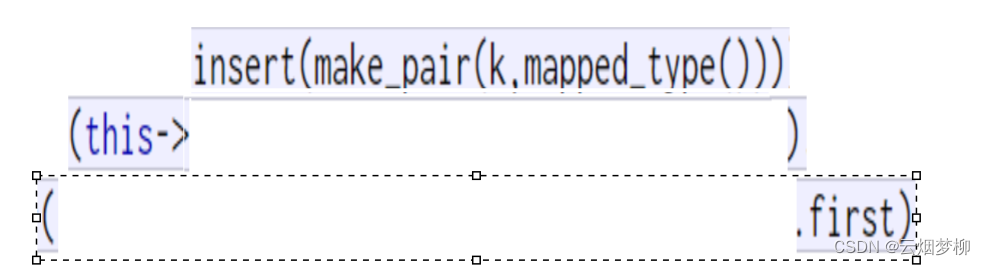
 库中的返回值是一个pair类型，其内部分别是一个i迭代器和bool类型，那么这样的作法我们也就理解了，现在我们要修改一下insert。

 set中虽然用不到【】但其内部和set是一样定义的。

更改结果如下(RBTree内）

typedef _RBTreeIterator<T, T&, T*> iterator;
typedef _RBTreeIterator<T, const T&, const T*> const_iterator;iterator begin()
{Node* left = _root;while (left && left->_left){left = left->_left;}return iterator(left);
}iterator end()
{return iterator(nullptr);
}//bool Insert(const T& data)
pair<iterator, bool> Insert(const T& data)
{if (!_root){_root = new Node(data);_root->_co = Black;//如果成功，返回成功节点的迭代器和truereturn make_pair(iterator(_root), true);}Node* cur = _root;Node* parent = nullptr;while (cur){//if (cur->_data.first < data.first)if (kot(cur->_data)< kot(data)){parent = cur;cur = cur->_right;}//else if (cur->_data.first > data.first)else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{//return false;return make_pair(iterator(cur), false);}}cur = new Node(data);cur->_co = Red;//注意这里cur可能因为旋转，改变了原来的位置，所以需要提前记录一下Node* newnode = cur;//if (parent->_data.first < cur->_data.first)if (kot(parent->_data) < kot(cur->_data)){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//开始判断是否需要变色while (parent && parent->_co == Red){Node* grand = parent->_parent;if (parent == grand->_left){Node* uncle = grand->_right;if (uncle && uncle->_co == Red){//这里只变色就好parent->_co = uncle->_co = Black;grand->_co = Red;cur = grand;parent = cur->_parent;}else{if (cur == parent->_left){_RotateR(grand);grand->_co = Red;parent->_co = Black;}else{_RotateL(parent);_RotateR(grand);cur->_co = Black;grand->_co = Red;}break;}}else{Node* uncle = grand->_left;if (uncle && uncle->_co == Red){//这里只变色就好parent->_co = uncle->_co = Black;grand->_co = Red;cur = grand;parent = cur->_parent;}else{if (cur == parent->_right){_RotateL(grand);grand->_co = Red;parent->_co = Black;}else{_RotateR(parent);_RotateL(grand);cur->_co = Black;grand->_co = Red;}break;}}}_root->_co = Black;//return true;return make_pair(iterator(newnode), true);
}

map和set内

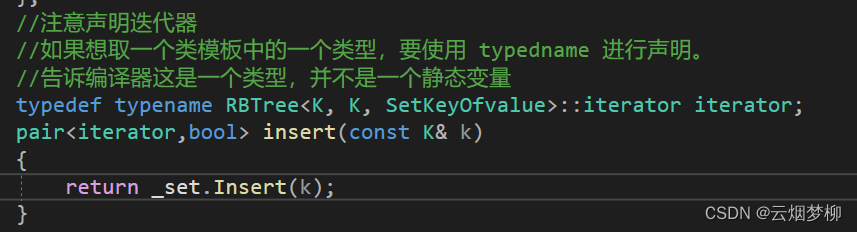
第四步，解引用返回，因为first是个迭代器类型，对其解引用返回data值 

但是我们自己实现时，应该返回其data值里面的second，因为map的特性，只有second可以被修改。

故可以得出以下代码：
  注意，这是定义在map里面的，并非定义在迭代器里面

	V& operator[](const K& key){pair<iterator, bool> result = insert(make_pair(key, V()));//如果存在，则插入失败//如果不存在，则插入数据//无论是否存在,都返回 second;return result.first->second;}

 四.源代码+ 测试用例

其实map和set还有很多可以值得封装的地方，这里我们给出一个比较完整的源代码：

map：
 

#pragma once
#include"RBTree.h"
using namespace MyRBTree;namespace MyMap
{template<class K,class V>class Map{public:struct MapKeyOfvalue{const K& operator()(const pair<K, V>& kv){return kv.first;}};//注意声明迭代器//如果想取一个类模板中的一个类型，要使用 typedname 进行声明。//告诉编译器这是一个类型，并不是一个静态变量typedef typename RBTree<K, pair<K, V>, MapKeyOfvalue>::iterator iterator;typedef typename RBTree<K, pair<K, V>, MapKeyOfvalue>::const_iterator const_iterator;pair<iterator,bool> insert(const pair<K,V> &kv){return _map.Insert(kv);}void Inorder(){_map.Inorder();}void IsBalance(){_map.IsBalance();}V& operator[](const K& key){pair<iterator, bool> result = insert(make_pair(key, V()));//如果存在，则插入失败//如果不存在，则插入数据//无论是否存在,都返回 second;return result.first->second;}iterator begin(){return _map.begin();}iterator end(){return _map.end();}{return _map.begin();}iterator end(){return _map.end();}private:RBTree<K, pair<K,V>, MapKeyOfvalue> _map;};
}

set：
 

#pragma once
#include"RBTree.h"using namespace MyRBTree;namespace MySet
{template<class K>class Set{public:struct SetKeyOfvalue{const K& operator()(const K& key){return key;}};//注意声明迭代器//如果想取一个类模板中的一个类型，要使用 typedname 进行声明。//告诉编译器这是一个类型，并不是一个静态变量typedef typename RBTree<K, K, SetKeyOfvalue>::const_iterator iterator;typedef typename RBTree<K, K, SetKeyOfvalue>::const_iterator const_iterator;pair<iterator,bool> insert(const K& k){return _set.Insert(k);}void Inorder(){_set.Inorder();}void IsBalance(){_set.IsBalance();}private:RBTree<K, K, SetKeyOfvalue> _set;};
}

红黑树：

#pragma once
#include<iostream>
using namespace std;namespace MyRBTree
{enum Color{Red,Black};//直接实现kv模型的红黑树template<class T>struct RBTreeNode{RBTreeNode(const T& data):_co(Red), _left(nullptr), _right(nullptr), _parent(nullptr), _data(data){}Color _co;RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;T _data;};//	   节点数据	 引用/const引用  指针/const指针template <class T, class Ref, class Ptr>struct _RBTreeIterator{typedef RBTreeNode<T> Node;typedef _RBTreeIterator<T, Ref, Ptr> self;Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}bool operator==(const self& s){return _node == s._node;}bool operator!=(const self& s){return _node != s._node;}self& operator++() //迭代器++，依旧返回迭代器{//如果右子树存在if (_node->_right){Node* left = _node->_right;//则寻找右子树的最左节点while (left->_left){left = left->_left;}_node = left;}//如果右子树不存在else{//找孩子不是父亲右节点的节点Node* parent = _node->_parent;Node* cur = _node; //一定要先判断parent是否存在，以此来避免越界while (parent&&cur == parent->_right){cur = cur->_parent;parent = parent->_parent;}_node = parent;}return *this;}//迭代器后置++self operator++(int){self it(_node);++(*this);return it;}self& operator--(){//如果左子树存在if (_node->left){//找左子树的最右节点Node* right = _node->_left;while (right->_right){right = right->_right;}_node = right;}//如果左子树不存在else{//找孩子不是父亲左节点的节点Node* parent = _node->parent;Node* cur = _node;while (parent&&parent->_left == cur){cur = cur->_parent;parent = parent->_parent;}_node = parent;}return *this;}//后置--self operator--(int){self it(_node);--(*this);return it;}_RBTreeIterator(Node* node):_node(node){}Node* _node;};template<class K, class T, class KeyOfValue>class RBTree{public:typedef RBTreeNode<T> Node;typedef _RBTreeIterator<T, T&, T*> iterator;typedef _RBTreeIterator<T, const T&, const T*> const_iterator;iterator begin(){Node* left = _root;while (left && left->_left){left = left->_left;}return iterator(left);}iterator end(){return iterator(nullptr);}const_iterator cbegin() const{Node* left = _root;while (left && left->_left){left = left->_left;}return const_iterator(left);}const_iterator cend() const {return const_iterator(nullptr);}//bool Insert(const T& data)//pair<iterator,bool> Insert(const T& data)	pair<Node*, bool> Insert(const T& data) //因为set中的iterator是 const迭代器，不可以转化为iterator类型，变成node在返回时可以构造出iterator和const迭代器{if (!_root){_root = new Node(data);_root->_co = Black;//如果成功，返回成功节点的迭代器和truereturn make_pair(_root, true);}Node* cur = _root;Node* parent = nullptr;while (cur){//if (cur->_data.first < data.first)if (kot(cur->_data)< kot(data)){parent = cur;cur = cur->_right;}//else if (cur->_data.first > data.first)else if (kot(cur->_data) > kot(data)){parent = cur;cur = cur->_left;}else{//return false;return make_pair(cur, false);}}cur = new Node(data);cur->_co = Red;//注意这里cur可能因为旋转，改变了原来的位置，所以需要提前记录一下Node* newnode = cur;//if (parent->_data.first < cur->_data.first)if (kot(parent->_data) < kot(cur->_data)){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//开始判断是否需要变色while (parent && parent->_co == Red){Node* grand = parent->_parent;if (parent == grand->_left){Node* uncle = grand->_right;if (uncle && uncle->_co == Red){//这里只变色就好parent->_co = uncle->_co = Black;grand->_co = Red;cur = grand;parent = cur->_parent;}else{if (cur == parent->_left){_RotateR(grand);grand->_co = Red;parent->_co = Black;}else{_RotateL(parent);_RotateR(grand);cur->_co = Black;grand->_co = Red;}break;}}else{Node* uncle = grand->_left;if (uncle && uncle->_co == Red){//这里只变色就好parent->_co = uncle->_co = Black;grand->_co = Red;cur = grand;parent = cur->_parent;}else{if (cur == parent->_right){_RotateL(grand);grand->_co = Red;parent->_co = Black;}else{_RotateR(parent);_RotateL(grand);cur->_co = Black;grand->_co = Red;}break;}}}_root->_co = Black;//return true;return make_pair(newnode, true);}void Inorder(){_Inorder(_root);}bool IsBalance(){return _IsBalance();}Node* Find(const K& key){//KeyOfValue kot;Node* cur = _root;while (cur){//if (cur->_data.first < key)if (kot(cur->_data) < key){cur = cur->_right;}//else if (cur->_data.first > key)else if (kot(cur->_data) > key){cur = cur->_left;}else{return cur;}}return nullptr;}//求最左节点Node* LeftMost(){Node* cur = _root;while (cur && cur->_left){cur = cur->_left;}return cur;}//求最右节点Node* RightMost(){Node* cur = _root;while (cur && cur->_right){cur = cur->_right;}return cur;}private:bool _IsBalance(){if (!_root) return true;if (_root->_co == Red){cout << "根节点为红色" << endl;return false;}int BlackSum = 0;Node* cur = _root;while (cur){if (cur->_co == Black) BlackSum++;cur = cur->_left;}return _Check(_root, 0, BlackSum);}bool _Check(Node* root, int Blacknum, int BlackSum){if (!root){if (Blacknum != BlackSum){cout << "某条路径黑色节点的数量不相等" << endl;return false;}return true;}if (root->_co == Black){++Blacknum;}if (root->_co == Red && root->_parent && root->_parent->_co == Red){cout << "存在连续的红色节点" << endl;return false;}return _Check(root->_left, Blacknum, BlackSum) && _Check(root->_right, Blacknum, BlackSum);}//直接创建一个全局变量，递归遍历的话消耗太高//注意把前面我们更改的删除//KeyOfValue kot;void _Inorder(Node* root){if (!root){return;}//这里我们也要更改一下_Inorder(root->_left);//cout << root->_data.first << ":" << endl;cout <<kot(root->_data) <<" ";_Inorder(root->_right);}void _RotateR(Node* parent){Node* SubL = parent->_left;Node* SubLR = SubL->_right;parent->_left = SubLR;if (SubLR) SubLR->_parent = parent;Node* pparent = parent->_parent;SubL->_right = parent;parent->_parent = SubL;if (_root == parent){_root = SubL;SubL->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = SubL;}else{pparent->_right = SubL;}SubL->_parent = pparent;}}void _RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;subR->_left = parent; //将subR的左指针指向parentNode* pparent = parent->_parent;parent->_parent = subR;//将parent的父指针指向subRif (subRL)subRL->_parent = parent;if (_root == parent) //判断parent是否是头节点{_root = subR;subR->_parent = nullptr;}else{if (pparent->_left == parent){pparent->_left = subR;}else{pparent->_right = subR;}subR->_parent = pparent;}}KeyOfValue kot;Node* _root = nullptr;};
}

相关文章：

C++ 红黑树的封装

一.map/set的封装 在实现了红黑树的部分功能后&#xff0c;我们可以便可以将红黑树作为底层结构来封装map 和 set &#xff0c;但是问题也随之而来。我们都知道map是k-v的数据模型&#xff0c;而set是k的数据模型&#xff0c;我们难道要去使用两棵红黑树来封装吗&#xff1f;显…...

编程日记 2023/12/4 20:03:50

MongoDB快速入门及其SpringBoot实战

MongoDB快速入门及其SpringBoot实战 MongoDB简介 MongoDB 是一个基于分布式文件存储的数据库。由 C 语言编写。旨在为 WEB 应用提供可扩展的高性能数据存储解决方案。 MongoDB是一个开源、高性能、无模式的文档型数据库&#xff0c;当初的设计就是用于简化开发和方便扩展&am…...

编程日记 2023/12/4 20:02:49

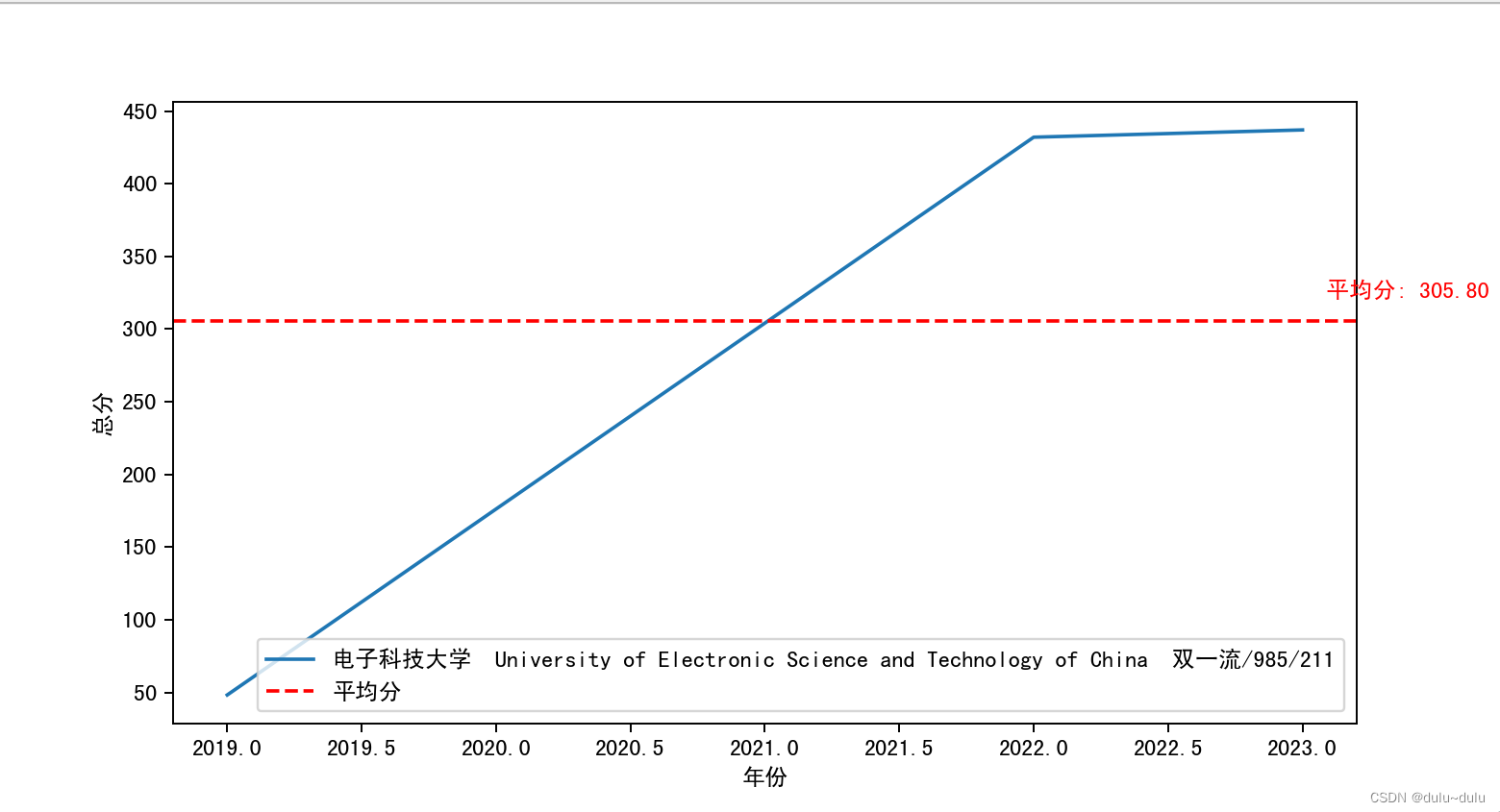
Python网络爬虫练习

爬取历年中国大学排名(前20名)&#xff0c;并随机选取一所高校画图展示其历年总分变化,并计算平均分&#xff0c;在图上展示该平均分直线&#xff1a; 代码如下&#xff1a; import matplotlib.pyplot as plt import pandas as pd import requests import randomdef main(yea…...

编程日记 2023/12/4 20:00:47

《opencv实用探索·九》中值滤波简单理解

1、引言 均值滤波、方框滤波、高斯滤波&#xff0c;都是线性滤波方式。由于线性滤波的结果是所有像素值的线性组合&#xff0c;因此含有噪声的像素也会被考虑进去&#xff0c;噪声不会被消除&#xff0c;而是以更柔和的方式存在。这时使用非线性滤波效果可能会更好。中值滤波是…...

编程日记 2023/12/4 19:59:47

PC行内编辑

点击编辑&#xff0c;行内编辑输入框出现&#xff0c;给列表的每条数据定义编辑标记&#xff0c;最后一定记得 v-model双向绑定&#xff0c;使数据回显。 步骤&#xff1a; 1、给行数据定义编辑标记 2、点击行编辑标记&#xff08;isedit&#xff09; 3、插槽根据标记渲染表单 …...

编程日记 2023/12/4 19:58:45

鸿蒙开发：Stage模型开发-应用/组件级配置以及UIAbility组件初步使用【鸿蒙专栏-20】

文章目录 Stage模型开发概述基本概念UIAbility组件和ExtensionAbility组件WindowStageContextAbilityStage开发流程应用组件开发了解进程模型了解线程模型应用配置文件应用版本声明配置Module支持的设备类型配置Module权限配置进阶应用配置...

编程日记 2023/12/4 19:57:45

Django回顾【五】

目录 一、多表操作 【1】基于对象的跨表查 【2】基于双下滑线的连表查 【3】related_name 二、聚合查询与分组查询 【1】聚合查询 【2】分组查询 三、F与Q查询 【1】F查询 【2】Q查询 四、其他字段和字段参数 【1】其他字段 【2】ORM字段参数 【3】ForeignKey 属…...

编程日记 2023/12/4 19:56:44

Python容器——字典

Key——Value 键值对...

编程日记 2023/12/4 19:55:43

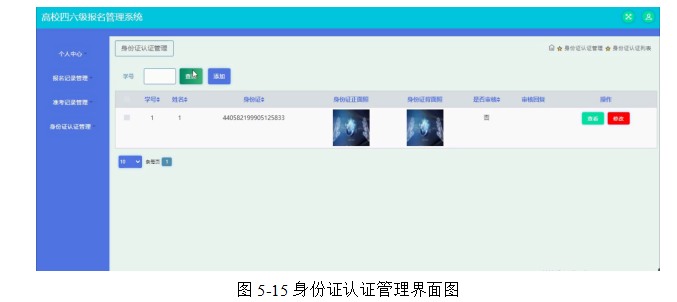
基于Java SSM框架实现实现四六级英语报名系统项目【项目源码+论文说明】

基于java的SSM框架实现四六级英语报名系统演示 摘要 本论文主要论述了如何使用JAVA语言开发一个高校四六级报名管理系统&#xff0c;本系统将严格按照软件开发流程进行各个阶段的工作&#xff0c;采用B/S架构&#xff0c;面向对象编程思想进行项目开发。在引言中&#xff0c;作…...

编程日记 2023/12/4 19:53:41

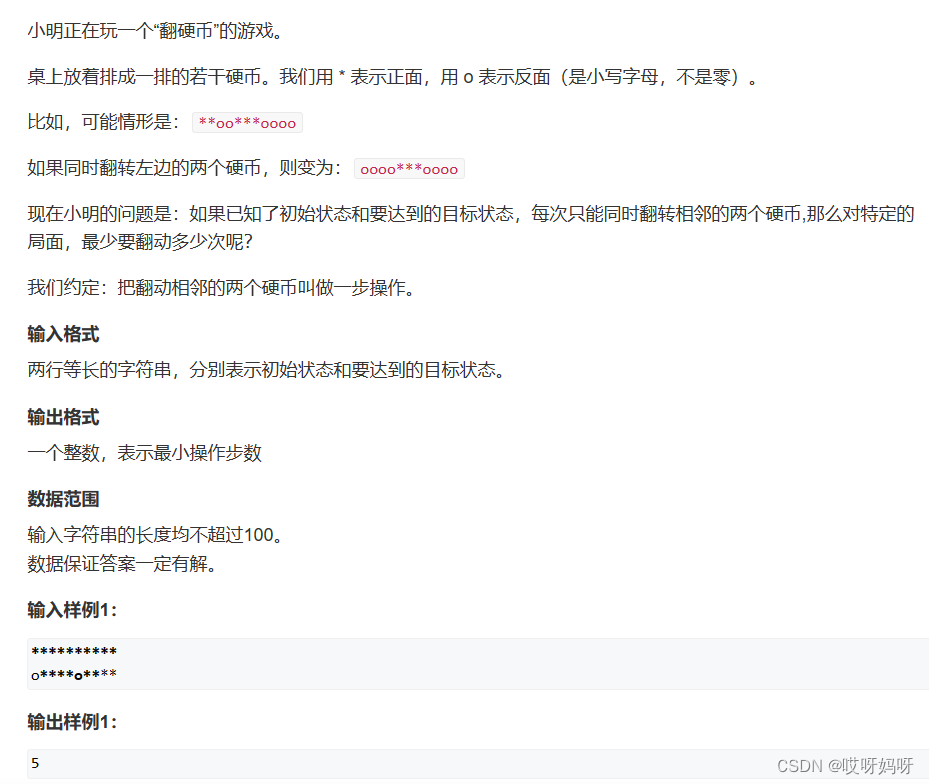
翻硬币(第四届蓝桥杯省赛C++B组)(java版)

//翻硬币,每次都会改变两个硬币的状态 //因此我们可以从前往后枚举,s1[i] 与 s2[i] 状态不同就改变它的状态 //同时s1[i 1] 与 s2[i 1] 的状态会因此改变 // 所以继续往下枚举s1[i 1] 与 s2[i 1] //因为题目有说必须有解,因此枚举到 n - 1位的时候&#xff0c;两个字符串的…...

编程日记 2023/12/4 19:52:41

原生GPT本地及云端部署方式保姆级教程

前提条件 部署必须要有一个超过1年的Github账号 本地服务部署 运行效果 部署方法 下载安装包 暂时无法在飞书文档外展示此内容 GitHub授权登录&#xff1a; https://dash.pandoranext.com/ 登录后是这个样子&#xff1a; 复制下面红框里面这个License Id 编辑Config.js…...

编程日记 2023/12/4 19:51:40

Docker容器（一）概述

一、虚拟化概述 1.1引⼊虚拟化技术的必要性 服务器只有5%的时间是在⼯作的&#xff1b;在其它时间服务器都处于“休眠”状态. 虚拟化前 每台主机⼀个操作系统; 软硬件紧密结合; 在同⼀个主机上运⾏多个应⽤程序通常会遭遇冲突; 系统的资源利⽤率低; 硬件成本⾼昂⽽且不够灵活…...

编程日记 2023/12/4 19:49:38

Facebook引流怎么做?写个脚本就好!

在当今的数字化时代&#xff0c;流量对于任何一个网站或应用程序来说都至关重要&#xff0c;Facebook&#xff0c;作为全球最大的社交网络平台&#xff0c;无疑是一个获取流量的绝佳场所&#xff0c;但是&#xff0c;如何有效地从Facebook引流呢?写个脚本就好了! 在本文中&am…...

编程日记 2023/12/4 19:46:36

自动化集成有哪些典型应用场景？

为什么要做自动化场景集成&#xff1f; 主要分为以下几点&#xff1a; 提高效率/减少错误&#xff1a;减少人工操作、人为错误、人力成本&#xff0c;提高生产效率、生产质量和稳定性。 提高可靠性&#xff1a;提高系统的可靠性和稳定性&#xff0c;减少系统故障和停机时间。…...

编程日记 2023/12/4 19:45:36

探讨几种在CentOS 7上实现文件上传的方法

最近服务器过期了&#xff0c;把之前服务器的数据库都备份了下来&#xff0c;现在准备迁移各种服务&#xff0c;这就涉及到文件传输。之前用得多的都是xshell里的xtp来传&#xff0c;校园网禁用了ssh协议&#xff0c;还有一大堆乱七八糟的协议&#xff0c;我一般用的代理方法或…...

编程日记 2023/12/4 19:44:35

AWS EC2使用 instance profile 访问S3

AWS EC2 instance可以使用instance profile 配置访问S3的权限。 然后就可以直接在EC2上执行 python代码或者AWS CLI去访问S3了。 唯一需要注意的地方是&#xff0c;申明region。 示例代码&#xff1a; aws s3 ls xxxx-s3-bucket --region xxx-region import boto3 client …...

编程日记 2023/12/4 19:43:33

python中函数式编程

文章目录 map()函数filter()函数reduce()函数 map()函数 当使用map()函数时&#xff0c;可以使用lambda表达式来定义一个简单的转换函数。 以下是一个使用map()函数和lambda表达式的简单示例&#xff1a; numbers [1, 2, 3, 4, 5] squared_numbers map(lambda x: x**2, nu…...

编程日记 2023/12/4 19:42:32

Java_JDK8到JDK21各版本发行时间及重要特性

Java_JDK8到JDK21各版本发行时间及重要特性 背景JDK8新特性(2014年3月)JDK9新特性&#xff08;2017年9月&#xff09;JDK10新特性&#xff08;2018年3月&#xff09;JDK11新特性&#xff08;2018年9月&#xff09;&#xff08;LTS版本&#xff09;JDK12新特性&#xff08;2019年…...

编程日记 2023/12/4 19:41:31

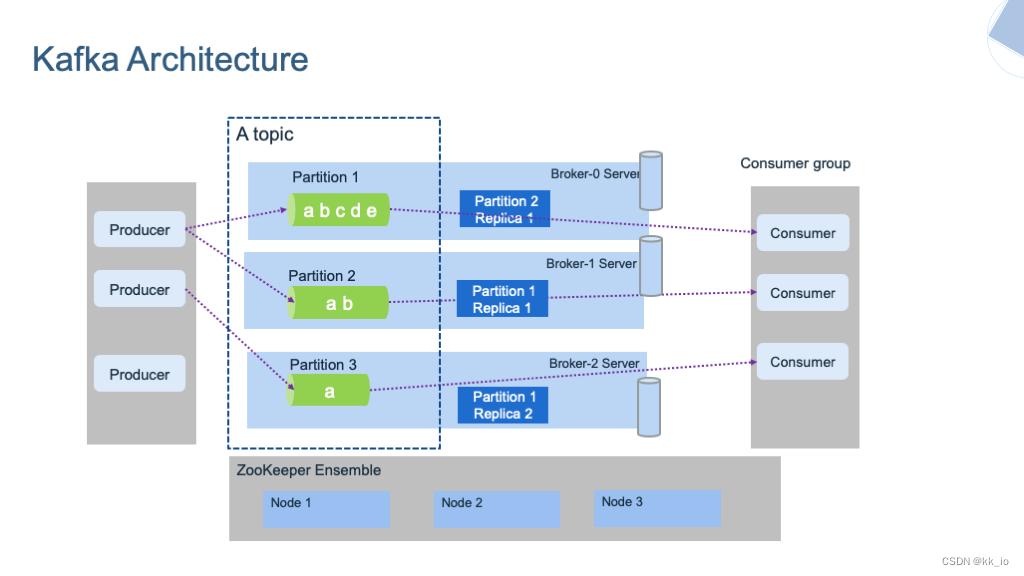
03 数仓平台 Kafka

kafka概述 定义 Kafka 是一个开源的分布式事件流平台&#xff08;Event Streaming Plantform&#xff09;&#xff0c;主要用于大数据实时领域。本质上是一个分布式的基于发布/订阅模式的消息队列&#xff08;Message Queue&#xff09;。 消息队列 在大数据场景中主要采用…...

编程日记 2023/12/4 19:37:28

2023年全国硕士研究生入学统一考试管理类专业学位联考逻辑试题——解析版

文章目录 2023年全国硕士研究生入学统一考试管理类专业学位联考逻辑试题三、逻辑推理真题（2023-26）真题（2023-27）真题（2023-28）真题（2023-29）真题（2023-30）真题（2023-31-32）真题（2023-33）真题（2023-34）真题（2023-35）真题（2023-36）真题（2023-37-38...

编程日记 2023/12/4 19:35:26

Docker 离线安装指南

参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性&#xff0c;不同版本的Docker对内核版本有不同要求。例如&#xff0c;Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本&#xff0c;Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

编程新知 2025/7/6 7:25:51

日语学习-日语知识点小记-构建基础-JLPT-N4阶段（33）：にする

日语学习-日语知识点小记-构建基础-JLPT-N4阶段（33）：にする 1、前言（1）情况说明（2）工程师的信仰2、知识点（1）　にする1，接续：名词＋にする2，接续：疑问词＋にする3，（A）は（B）にする。（2）復習：（1）复习句子（2）ために　＆　ように（３）そう（４）にする3、…...

编程新知 2025/6/17 10:46:36

centos 7 部署awstats 网站访问检测

一、基础环境准备&#xff08;两种安装方式都要做&#xff09; bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats&#xff0…...

编程新知 2025/7/7 13:07:24

Mac软件卸载指南，简单易懂！

刚和Adobe分手&#xff0c;它却总在Library里给你写"回忆录"&#xff1f;卸载的Final Cut Pro像电子幽灵般阴魂不散&#xff1f;总是会有残留文件&#xff0c;别慌&#xff01;这份Mac软件卸载指南&#xff0c;将用最硬核的方式教你"数字分手术"&#xff0…...

编程新知 2025/7/6 8:47:16

Axios请求超时重发机制

Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式&#xff1a; 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

编程新知 2025/6/21 10:09:08

聊一聊接口测试的意义有哪些？

目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开&#xff0c;首…...

编程新知 2025/7/4 20:21:33

全面解析各类VPN技术：GRE、IPsec、L2TP、SSL与MPLS VPN对比

目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec&#xff1f; IPsec VPN 5.1 IPsec传输模式&#xff08;Transport Mode&#xff09; 5.2 IPsec隧道模式&#xff08;Tunne…...

编程新知 2025/6/17 4:01:05

Java多线程实现之Thread类深度解析

Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

编程新知 2025/6/27 3:48:34

【C++特殊工具与技术】优化内存分配(一)：C++中的内存分配

目录 一、C 内存的基本概念​ 1.1 内存的物理与逻辑结构​ 1.2 C 程序的内存区域划分​ 二、栈内存分配​ 2.1 栈内存的特点​ 2.2 栈内存分配示例​ 三、堆内存分配​ 3.1 new和delete操作符​ 4.2 内存泄漏与悬空指针问题​ 4.3 new和delete的重载​ 四、智能指针…...

编程新知 2025/7/2 14:43:09

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案

目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后&#xff0c;迭代器会失效&#xff0c;因为顺序迭代器在内存中是连续存储的&#xff0c;元素删除后&#xff0c;后续元素会前移。 但一些场景中&#xff0c;我们又需要在执行删除操作…...

编程新知 2025/6/16 16:11:49