【matlab】QR分解
QR分解
给定一个m×n的矩阵A,其中m≥n,即矩阵A是高矩阵或者是方阵,QR分解将矩阵A分解为两个矩阵Q和R的乘积,其中矩阵Q是一个m×n的各列正交的矩阵,即QTQ=I,矩阵R是一个n×n的上三角矩阵,其对角线元素为正。
如果矩阵A是方阵,且各列线性无关,那么Q是一个正交矩阵,即QTQ=QQT=I。
QR分解有多种算法实现,包括Gram-Schmidt正交化方法、Householder变换方法和Givens旋转方法等,下面我们介绍Gram-Schmidt正交化方法和Householder变换方法,并在MATLAB平台上使用这两种算法来实现QR分解。
Gram-Schmidt算法
对于给定的n维向量a1,a2,……,an,Gram-Schmidt算法可以解决将其标准正交化的问题,即将一个线性无关的向量组转化为一个正交向量组,使得每个向量都与前面的向量正交(垂直),并且可以检验a1,a2,……,an是否是线性相关。
Gram-Schmidt算法的步骤如下:
- 初始化n维向量q1,q2,……,qn,其中q1=a1/||a1||2。
- 对于每个向量ai,i=2:n,进行正交化处理:qi= ai-( q1Tai)q1-…-( qi-1Tai)qi-1。
- 如果qi=0,说明ai是a1,a2,……,ai-1的一个线性组合,可以结束算法了。
- 否则将qi进行单位化,qi=qi/||qi||2。
如果步骤③没有结束,那么说明a1,a2,……,an是线性无关的,而且得到了一个正交向量组q1,q2,……,qn。
Gram-Schmidt算法实现的QR分解
对于给定矩阵A,其列向量线性无关,Gram-Schmidt算法实现的QR分解步骤如下:
- 对列向量a1,a2,……,an按照Gram-Schmidt方法进行正交化。
- 对上一步得到的正交化向量组进行单位化得到各列正交的矩阵Q。
- 根据A=QR,QTQ=I→R=QTA,得到上三角矩阵R
MATLAB验证Gram-Schmidt算法实现QR分解稳定性
通过直观的方法来观察到Gram-Schmidt QR分解的正交性偏差,理论上通过Gram-Schmidt算法后可以得到列向量线性无关的各列正交的矩阵Q,即QTQ=I,我们可以直接计算QTQ,看看计算结果与单位矩阵I的差距
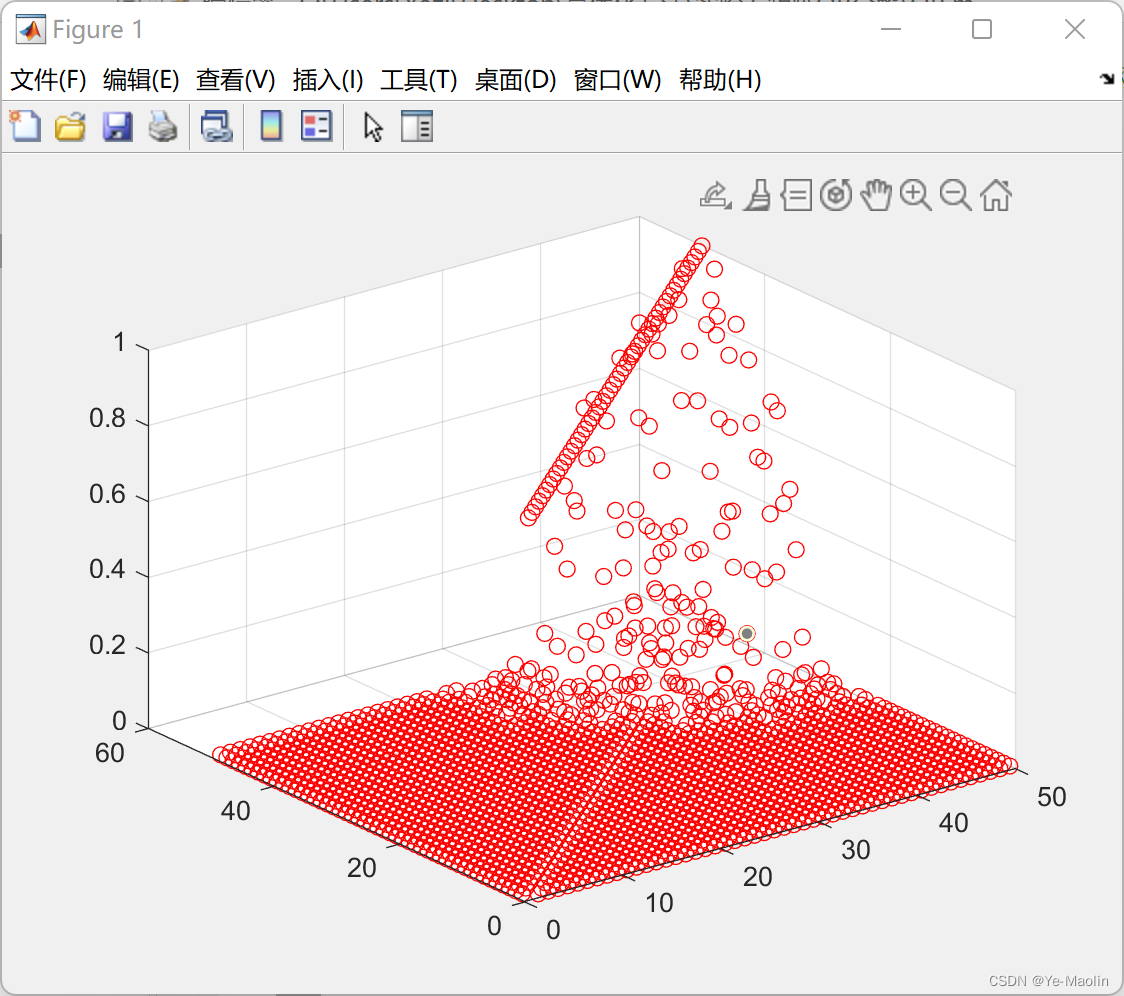
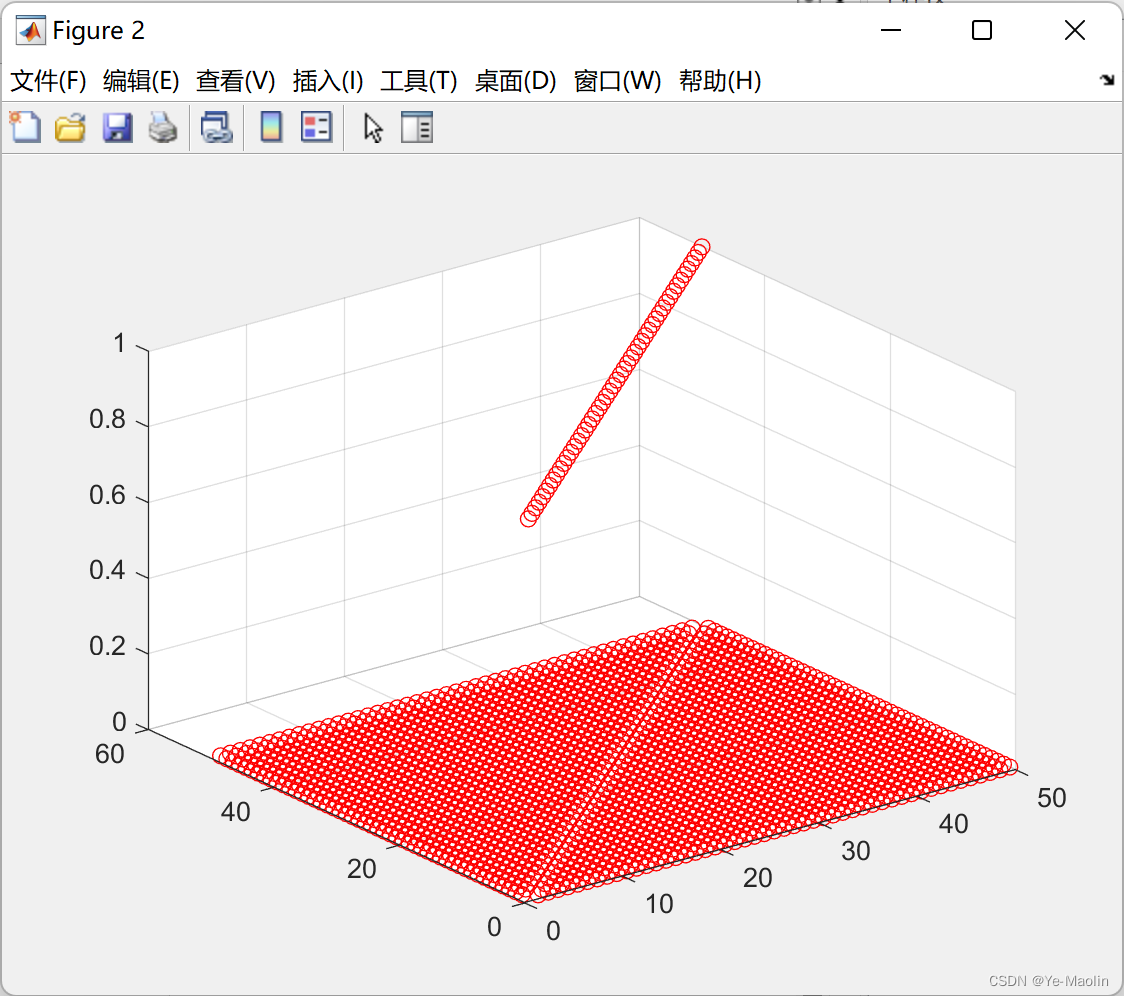
左图是QTQ的计算结果,有图是单位矩阵I,可见由于浮点数存储的舍入误差,随着k增大,积累的误差越大,矩阵Q逐渐失去正交性
clc,clear;
load MatrixA.mat;
[m,n]=size(A);
Q=zeros(m,n);
R=zeros(n,n);
%% Gram-Schmidt QR分解
for k=1:nR(1:k-1,k)=Q(:,1:k-1)'*A(:,k); %求出R(1,K) - R(K-1,K)v=A(:,k)-Q(:,1:k-1)*R(1:k-1,k); %求出正交化向量qR(k,k)=norm(v); %求出R(K,K)Q(:,k)=v/R(k,k); %单位化向量q
end
%% 正交性偏差
figure(1);
E = zeros(1,n);
for k=2:nmax = 0;for i=1:k-1temp = abs(Q(:,i)' * Q(:,k));if temp > maxmax = temp;endendE(1,k)=max;
end
plot(E)
%% 比较QTQ和I
QTQ=Q'*Q;
figure(2);
for i=1:nfor j=1:nscatter3(i,j,QTQ(i,j),'red');hold on;end
end
zlim([0,1]);
I=eye(n);
figure(3);
for i=1:nfor j=1:nscatter3(i,j,I(i,j),'red');hold on;end
end
zlim([0,1]);Householder变换
Householder变换是一种镜面反射变换,householder变换矩阵为H = I - 2wwT,如何理解这个变换矩阵呢,考虑向量w,那么有:
Hw = (I - 2wwT)w = w - 2w(wTw) = - w
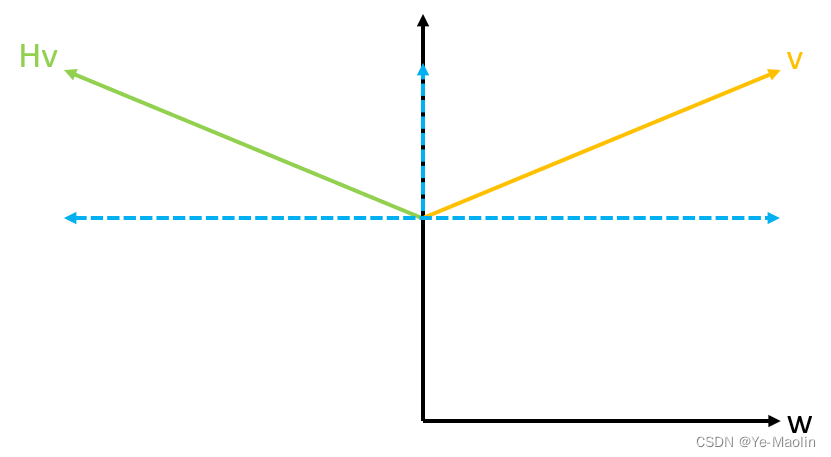
这说明对于平行于w的向量,householder变换的作用是将其反向,再考虑与向量w垂直的向量v,即wTv=0,那么有:
Hv = (I - 2wwT)v = v - 2w(wTv) = v
这说明对于垂直于w的向量,householder变换的作用就是对其不起任何作用,那么对于一个普通的向量v来说,平行于w的分量被householder反向,垂直于w的分量不变,那么最终的效果就是将向量v作关于法向量为w的平面的镜像对称
基于Householder变换的QR分解

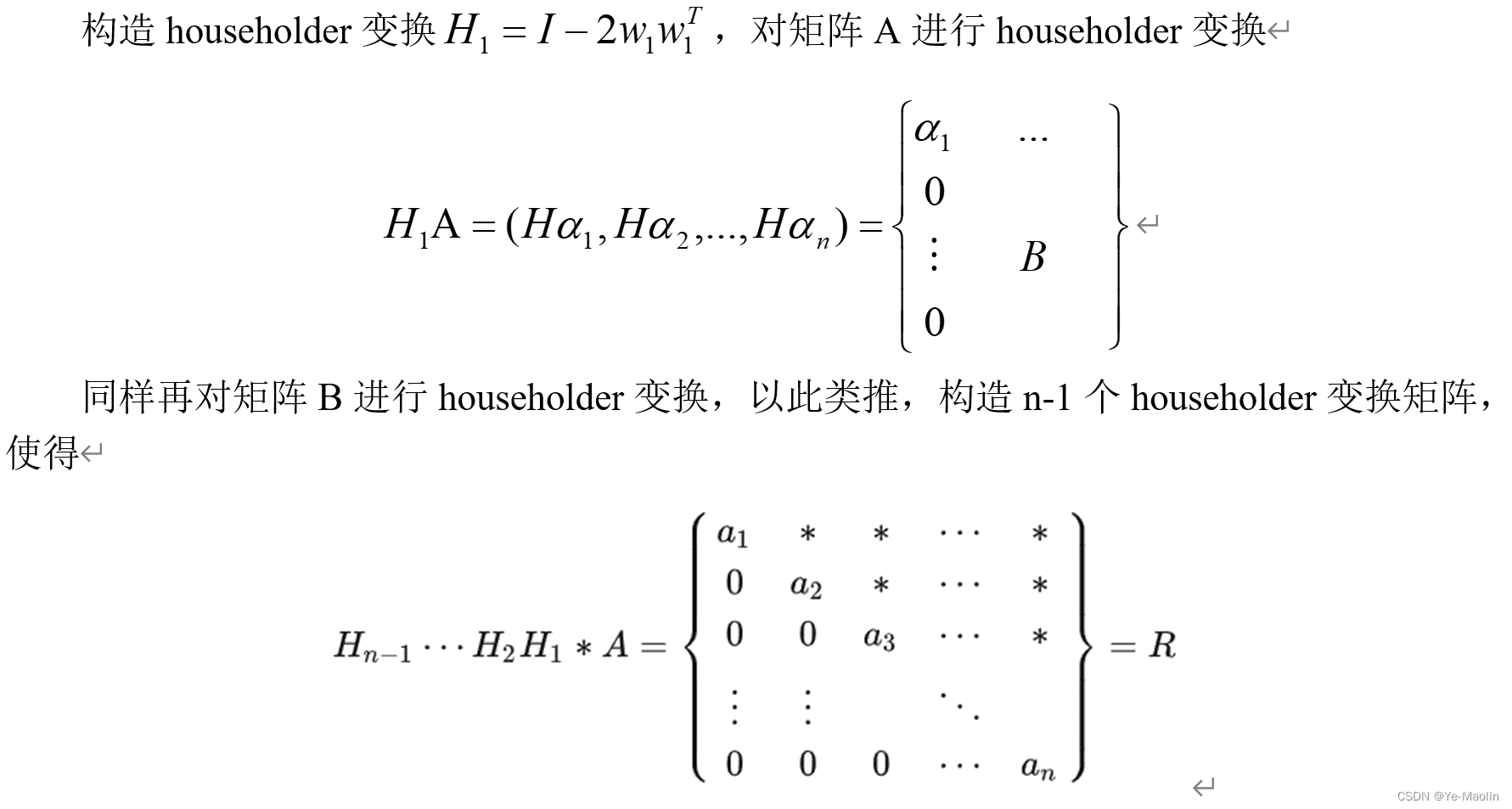
因为H=H-1,所以A=H1H2,…,Hn-1R,即Q= H1H2,…,Hn-1,再根据A=QR,QTQ=I→R=QTA。
再来比较一下QTQ与单位矩阵I的差距,结果如图所示,左边的是计算出来的QTQ,右边是单位矩阵I

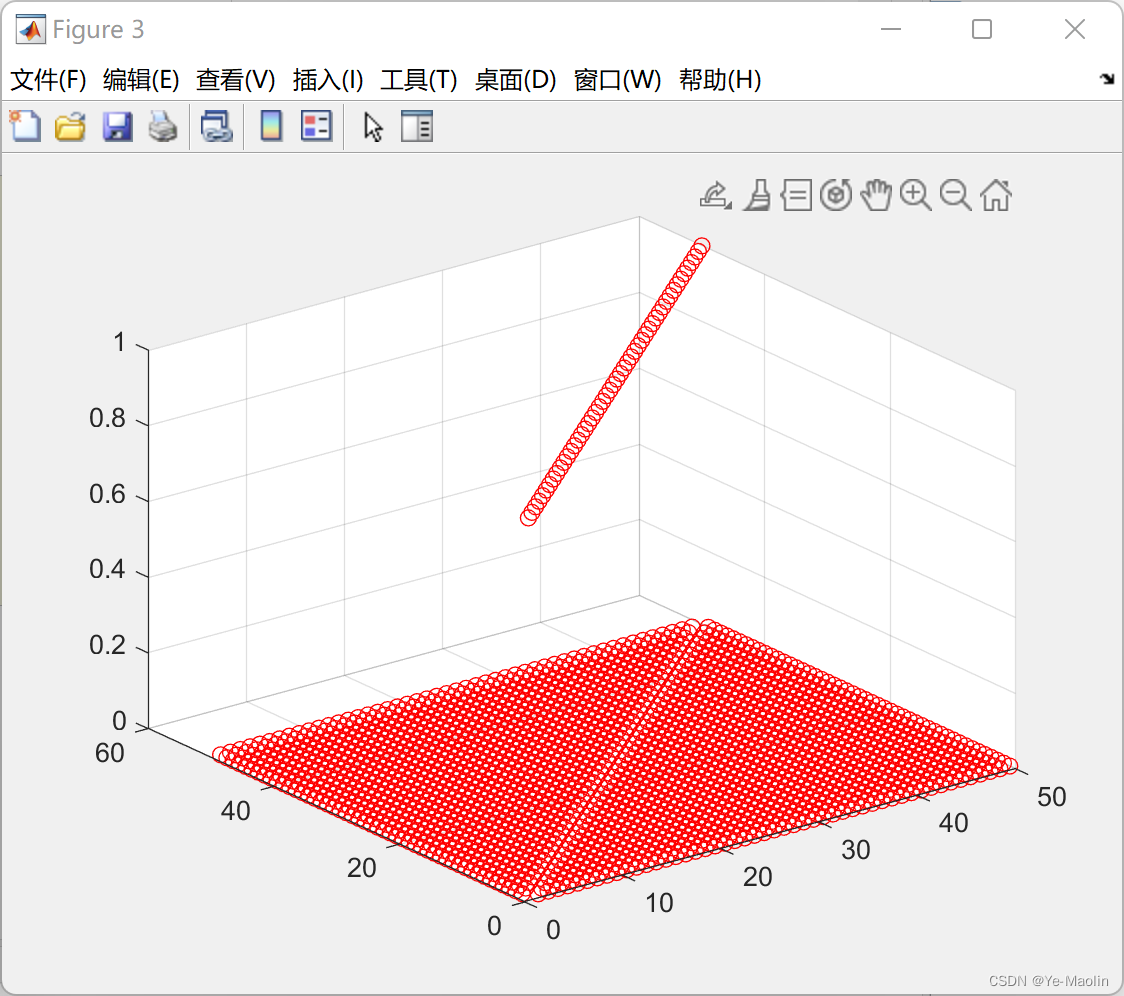
结果QTQ和I基本一样,可见相比其他分解方法,Householder算法能够减小舍入误差的累积,提高计算结果的稳定性。此外,该算法的时间复杂度较低,具备较高的计算效率。
clc,clear;
load MatrixA.mat;
[m,n]=size(A);
Q=zeros(m,n);
R=zeros(n,n);
%% Householder QR分解
[Q,R]=qr(A); % matlab库函数就是用的Householder
%% 正交性偏差
figure(1);
E = zeros(1,n);
for k=2:nmax = 0;for i=1:k-1temp = abs(Q(:,i)' * Q(:,k));if temp > maxmax = temp;endendE(1,k)=max;
end
plot(E)
%% 比较QTQ和I
QTQ=Q'*Q;
figure(2);
for i=1:nfor j=1:nscatter3(i,j,QTQ(i,j),'red');hold on;end
end
zlim([0,1]);
I=eye(n);
figure(3);
for i=1:nfor j=1:nscatter3(i,j,I(i,j),'red');hold on;end
end
zlim([0,1]);判断矩阵是否可逆
判断矩阵是否可逆有以下几种方法:
- 存在一个矩阵B,使得AB=BA=I,确实可逆。
- 矩阵行列式不为0,可逆。
- 矩阵满秩,可逆。
- 线性方程组Ax=0只有0解,可逆。
- 线性方程组Ax=b只有特解,可逆。
实际上如果一个方阵可以进行QR分解,那么这个方阵也是可逆的。
所以我们直接尝试对矩阵B进行QR分解,如果可以进行QR分解,那么矩阵B可逆。那么我们可以先假设矩阵B是可以进行QR分解,然后我们对矩阵B进行QR分解,显然矩阵B是可以进行QR分解的,这说明矩阵B是可逆的。
求逆
我们之前使用过高斯消元法来求解矩阵的逆,实际上也可以使用QR分解求矩阵的逆。由A = QR,QTQ = I,则A-1 = (QR)-1 = R-1Q-1 = R-1QT。
那么A-1就可以通过R-1QT得到,但是实际上我们并不需要计算R-1,让x= R-1QT,那么我们目标就是要得到x的结果,因为RR-1QT=QT,即Rx=QT,那么我们就需要求解这个线性方程组,由于R是上三角矩阵,所以直接回代就可以求出x,即求出R-1QT,即求出了A-1。
我们先用Gram-Schmidt算法实现的QR分解求解矩阵B的逆,将其与用MATLAB内置的求逆函数结果进行比较,结果如图所示,红色的圆圈是matlab内置的求逆函数计算出来的结果,绿色实心点是我们QR分解求出来的结果,如果二者重合说明计算结果相同。

可以看到基本上绿色的点都和红色的圆圈重合了,可见Gram-Schmidt算法QR分解求逆效果不错。
clc,clear;
load MatrixB.mat;
[m,n]=size(B);
Q=zeros(m,n);
R=zeros(n,n);
%% Gram-Schmidt QR分解
for k=1:nR(1:k-1,k)=Q(:,1:k-1)'*B(:,k); %求出R(1,K) - R(K-1,K)v=B(:,k)-Q(:,1:k-1)*R(1:k-1,k); %求出正交化向量qR(k,k)=norm(v); %求出R(K,K)Q(:,k)=v/R(k,k); %单位化向量q
end
%% 求逆
inverseQR=R\Q';
inverse=inv(B);
%% 画图比较
for i=0:n-1for j=1:nscatter(i*n+j,inverse(i+1,j),'red');hold on;scatter(i*n+j,inverseQR(i+1,j),'green','.');hold on;end
end我们再用之前的高斯消元法求解矩阵B的逆,将其与用MATLAB内置的求逆函数结果进行比较,结果如图所示
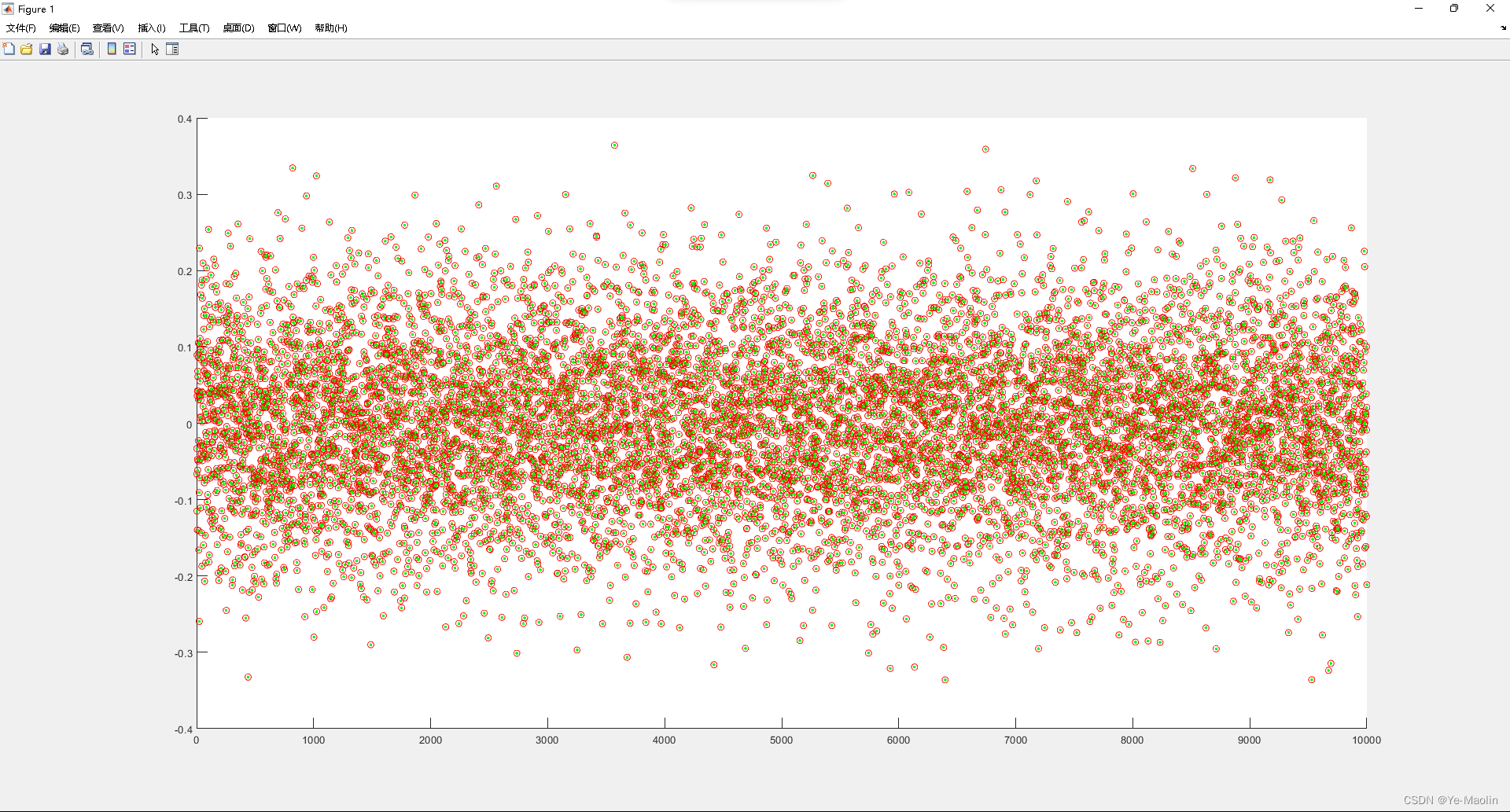
可见高斯消元法求逆的结果也很好,基本上绿色的点都和红色的圆圈重合了。
clc,clear;
load MatrixB.mat;
b=eye(50);
B_b=[B,b];
[n,m]=size(B_b);
for i=1:nfor j=m:-1:iB_b(i,j)=B_b(i,j)/B_b(i,i);endfor j=i+1:nfor k=m:-1:iB_b(j,k)=B_b(j,k)-B_b(j,i)*B_b(i,k);endend
% fprintf('第%d次消元\n',i);
% disp(rats(A_b));
end
for i=n-1:-1:1for j=i:-1:1for k=m:-1:n+1B_b(j,k)=B_b(j,k)-B_b(j,i+1)*B_b(i+1,k);endB_b(j,i+1)=0;end
% fprintf('第%d次回代\n',n-i);
% disp(rats(A_b));
end
gaussInverse=B_b(:,end-49:end);
inverse=inv(B);
%% 画图比较
for i=0:n-1for j=1:nscatter(i*n+j,inverse(i+1,j),'red');hold on;scatter(i*n+j,gaussInverse(i+1,j),'green','.');hold on;end
end再用householder算法实现的QR分解求解矩阵B的逆,将其与用MATLAB内置的求逆函数结果进行比较,结果如图所示。
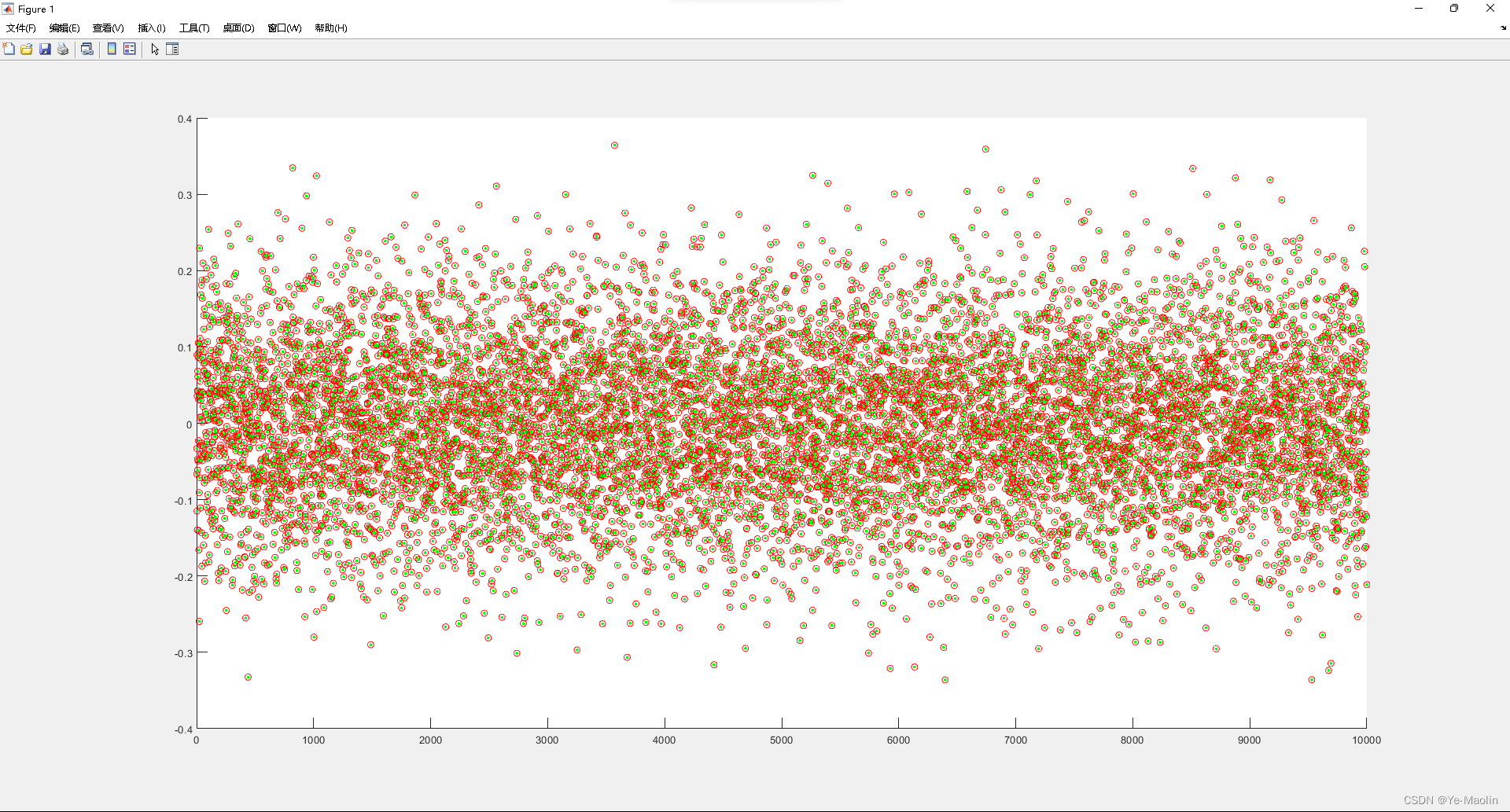
可见householder实现的QR分解求逆结果效果很好,基本上和matlab内置求逆函数结果相同,速度上也不慢。
clc,clear;
load MatrixB.mat;
[m,n]=size(B);
Q=zeros(m,n);
R=zeros(n,n);
%% Householder QR分解
[Q,R]=qr(B); % matlab库函数就是用的Householder
%% 求逆
inverseQR=R\Q';
inverse=inv(B);
%% 画图比较
for i=0:n-1for j=1:nscatter(i*n+j,inverse(i+1,j),'red');hold on;scatter(i*n+j,inverseQR(i+1,j),'green','.');hold on;end
end相关文章:

【matlab】QR分解
QR分解 给定一个mn的矩阵A,其中m≥n,即矩阵A是高矩阵或者是方阵,QR分解将矩阵A分解为两个矩阵Q和R的乘积,其中矩阵Q是一个mn的各列正交的矩阵,即QTQI,矩阵R是一个nn的上三角矩阵,其对角线元素为…...
Liunx系统使用超详细(三)
本篇内容开始逐渐描述有关liunx的各种命令的使用方法! 目录 一、目录和文件区别 1.1目录: 1.2文件: 1.3总结: 二、Linux命令的写法 三、linux命令清屏 四、pwd命令 五、ls命令 5.1 ls: 5.2 ls -l:…...

Kubernetes学习笔记-Part.06 Docker安装
目录 Part.01 Kubernets与docker Part.02 Docker版本 Part.03 Kubernetes原理 Part.04 资源规划 Part.05 基础环境准备 Part.06 Docker安装 Part.07 Harbor搭建 Part.08 K8s环境安装 Part.09 K8s集群构建 Part.10 容器回退 第六章 Docker安装 在master、worker、harbor上均需…...

现在的00后,实在是太卷了......
现在的小年轻真的卷得过分了。前段时间我们公司来了个00年的,工作没两年,跳槽到我们公司起薪18K,都快接近我了。后来才知道人家是个卷王,从早干到晚就差搬张床到工位睡觉了。 最近和他聊了一次天,原来这位小老弟家里条…...

Maven项目目录结构
项目结构 目录说明.ideaIDEA工具的配置文件.mvn用于运行Maven项目src源码文件夹target字节码文件夹.gitignore配置git忽略文件HELP.md自述文件mvnw运行Maven命令(Linux)mvnw.cmd运行Maven命令(Windows)pom.xml依赖管理文件 如图…...
感慨!一路从测试小白到现在的高级测试工程师,方向不对真的很艰辛
1 功能测试人员,也就是我们常常俗称的进行点点点测试工程师。前 1-2 年做功能测试,使用其他人开发的工具进行测试。这个阶段的测试工作都比较初级,严重依赖于别人开发的工具和系统。当系统进行升级换代的时候,强哥会明显的感觉到…...
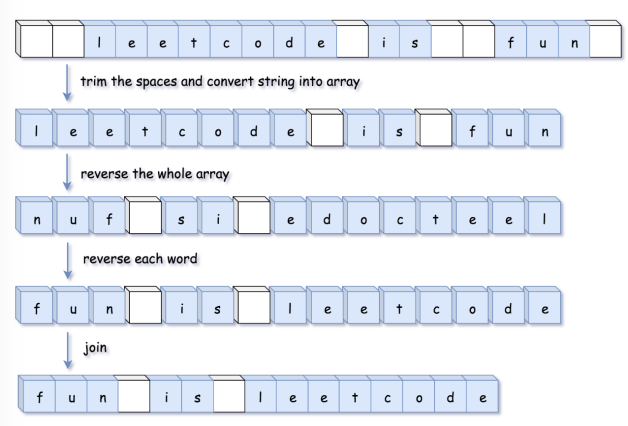
字符串经典基础面试题
关卡名 字符串经典基础面试题 我会了✔️ 内容 1.理解字符串反转的处理方法 ✔️ 2.熟练掌握回文串的判断方法 ✔️ 3.掌握字符串中搜索第一个唯一字符的方法 ✔️ 4.掌握判断是否互为字符串重排的处理技巧 ✔️ 1 反转的问题 我们知道反转是链表的一个重要考点…...

【华为OD题库-062】计算礼品发放的最小分组数目-java
题目 又到了一年的末尾,项目组让小明负责新年晚会的小礼品发放工作。为使得参加晚会的同时所获得的小礼品价值相对平衡,需要把小礼品根据价格进行分组,但每组最多只能包括两件小礼品,并且每个分组的价格总和不能超过一个价格上限。…...

[go 面试] 构建高效微服务通信:选择合适的通信方式
关注公众号【爱发白日梦的后端】分享技术干货、读书笔记、开源项目、实战经验、高效开发工具等,您的关注将是我的更新动力! 构建分布式系统或微服务架构时,服务间通信成为至关重要的一环。不同的通信方式各有优劣,因此在选择时需根…...

【华为OD题库-048】拔河比赛-java
题目 公司最近准备进行拔河比赛,需要在全部员工中进行挑选。选拔的规则如下: 1.按照身高优先、体重次优先的方式准备比赛阵容 2.规定参赛的队伍派出10名选手 请实现一个选拔队员的小程序。 输入为一个数组,记录了部门人员的身高、体重信息,如…...
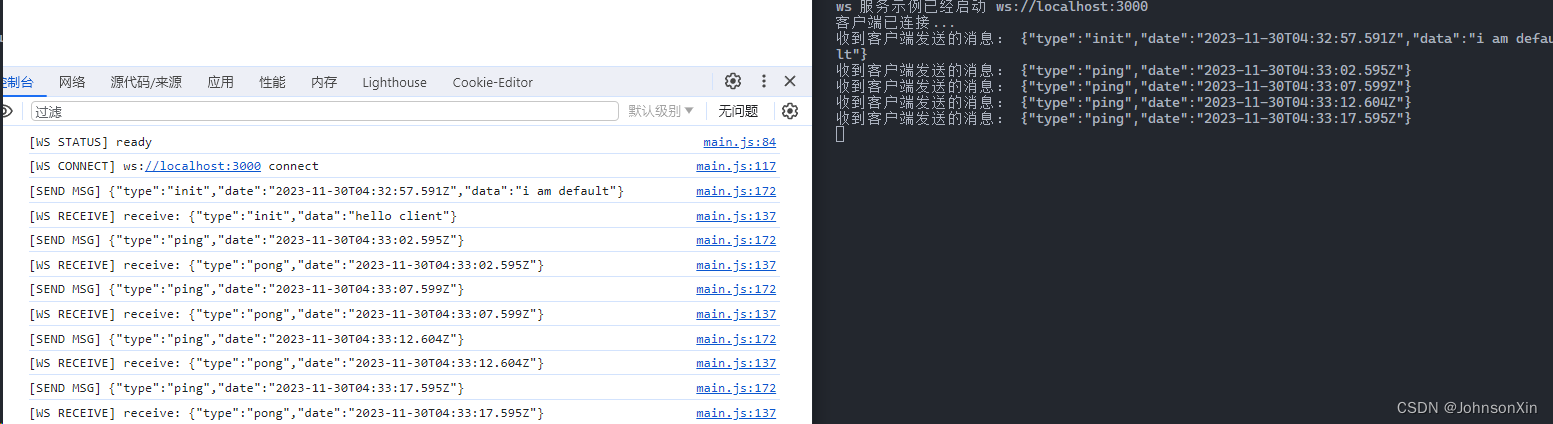
【WebSocket】通信协议基于 node 的简单实践和心跳机制和断线重连的实现
前后端 WebSocket 连接 阮一峰大佬 WebSocket 技术博客 H5 中提供的 WebSocket 协议是基于 TCP 的全双工传输协议。它属于应用层协议,并复用 HTTP 的握手通道。它只需要一次握手就可以创建持久性的连接。 那么什么是全双工呢? 全双工是计算机网络中的…...
【有ISSN、ISBN号!往届均已完成EI检索】第三届电子信息工程、大数据与计算机技术国际学术会议(EIBDCT 2024)
第三届电子信息工程、大数据与计算机技术国际学术会议(EIBDCT 2024) 2024 3rd International Conference on Electronic Information Engineering, Big Data and Computer Technology 第三届电子信息工程、大数据与计算机技术国际学术会议(…...
【Windows】使用SeaFile搭建本地私有云盘并结合内网穿透实现远程访问
1. 前言 现在我们身边的只能设备越来越多,各种智能手机、平板、智能手表和数码相机充斥身边,需要存储的数据也越来越大,一张手机拍摄的照片都可能有十多M,电影和视频更是按G计算。而智能设备的存储空间也用的捉襟见肘。能存储大量…...
Windows本地搭建WebDAV服务并使用内网穿透远程访问【无公网IP】
windows搭建WebDAV服务,并内网穿透公网访问【无公网IP】 文章目录 windows搭建WebDAV服务,并内网穿透公网访问【无公网IP】1. 安装IIS必要WebDav组件2. 客户端测试3. cpolar内网穿透3.1 打开Web-UI管理界面3.2 创建隧道3.3 查看在线隧道列表3.4 浏览器访…...

责任链设计模式
package com.jmj.pattern.responsibility;/*** 请假条类*/ public class LeaveRequest {//姓名private String name;//请假天数private int num;//请假内容private String content;public LeaveRequest(String name, int num, String content) {this.name name;this.num num;…...
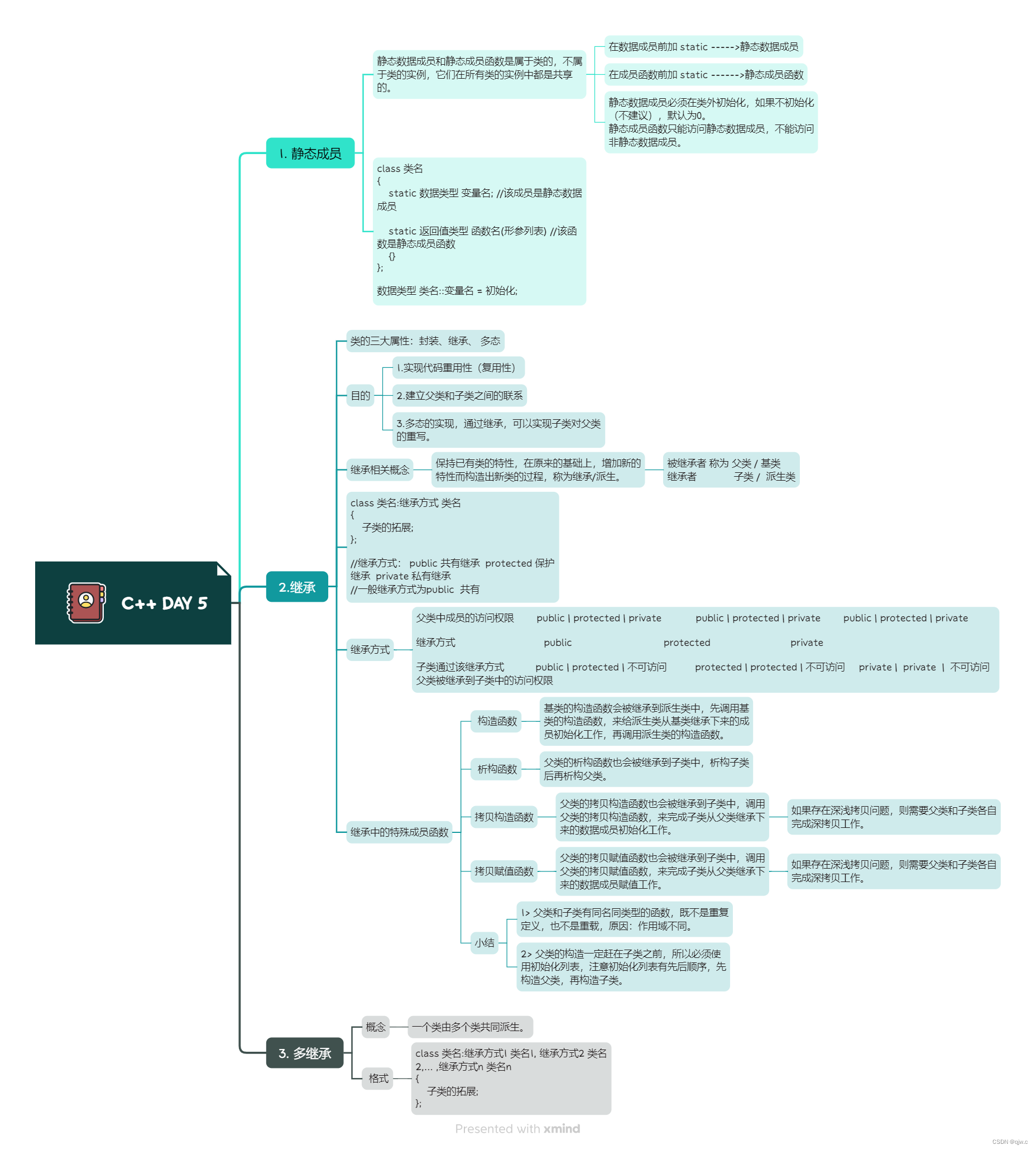
12.4 C++ 作业
完成沙发床的多继承 #include <iostream>using namespace std;//封装 沙发 类 class Sofa { private:string *sitting; public://无参构造函数Sofa(){cout << "Sofa::无参构造函数" << endl;}//有参构造函数Sofa(string s):sitting(new string(s)…...

基于ssm品牌会员在线商城源码
基于ssm品牌会员在线商城源码708 idea mysql数据库 navcat 开发技术:后端 ssm 后台管理 vue 用户端 vue.jshtml 演示视频: 基于ssm品牌会员在线商城源码 DROP TABLE IF EXISTS address; /*!40101 SET saved_cs_client character_set_client */; /…...

骨传导耳机音量大了有害吗?骨传导能保护听力吗?
无论是传统耳机还是骨传导耳机,只要使用音量过大,都会对有一定的损伤,然而由于骨传导耳机的传声原理和佩戴方式比较特殊,所以对人体的损伤比较小,想要知道骨传导耳机能否保护听力,就要先了解骨传导耳机的传…...
百望云供应链协同解决方案入选北大创新评论产业研究案例库
11月28日-29日,百望云受邀出席《北大创新评论》2023 Inno China 中国产业创新大会,从战略构建、生态塑造、科技创新等议题出发,与学术专家、产业专家、企业代表共赴盛会,思享汇聚。会上,《北大创新评论产业研究案例库&…...

selenium中元素定位正确但是操作失败,6种解决办法全搞定
selenium中元素定位正确但是操作失败的原因无外乎以下4种: 01 页面没加载好 解决方法:添加等待方法,如:time.sleep() 02 页面提交需要等待给数据后台 解决方法:添加等待方法,如:time.sleep(…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...
