当前位置： 首页 > news >正文

2分图匹配算法

news 文章来源：https://blog.csdn.net/yang_daxia/article/details/134693276 2024/11/19 23:18:51

定义

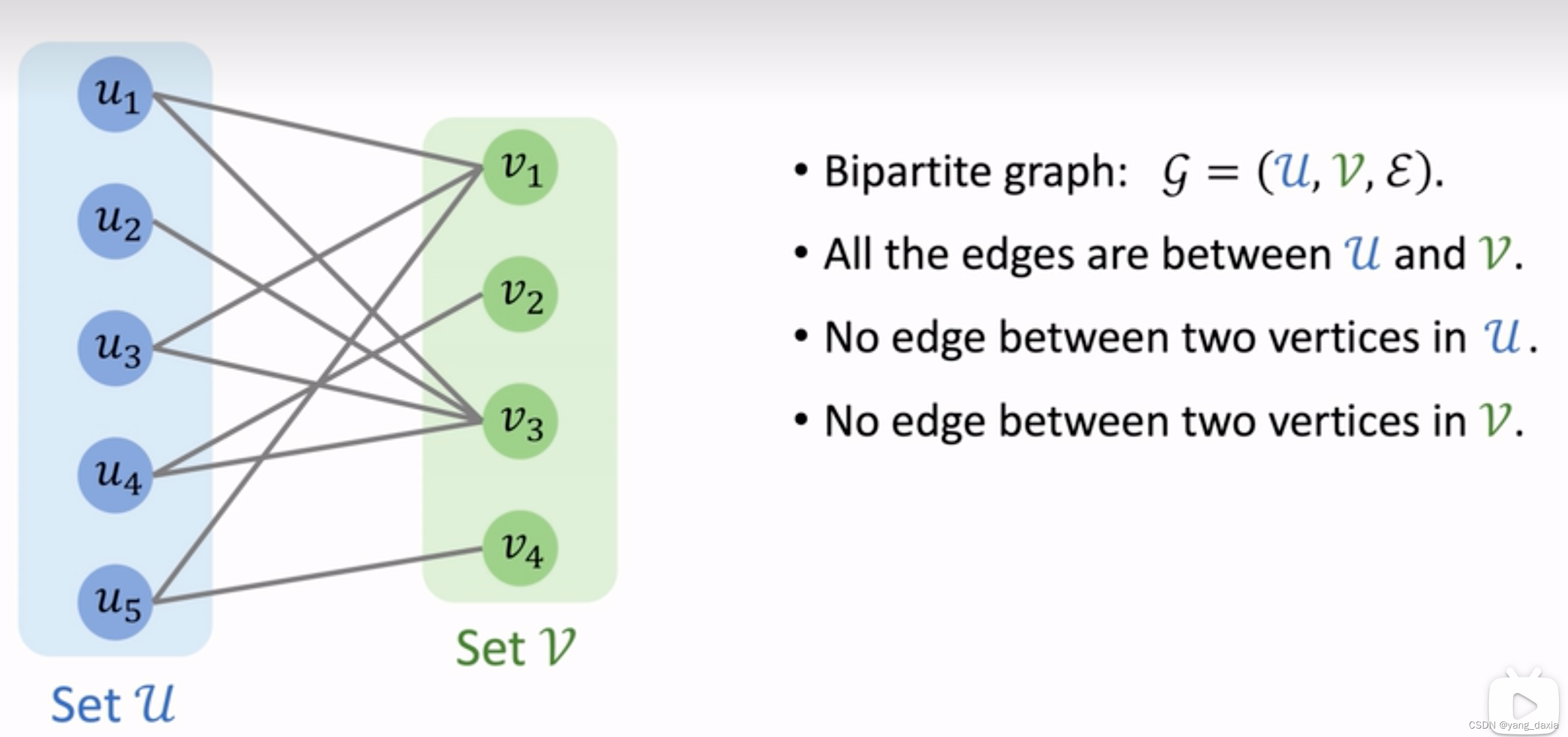
在这里插入图片描述

  • 节点u直接无边，v之间无边，边只存在uv之间。
  • 判断方法：BFS染色法，全部染色后，相邻边不同色

无权二部图中的最大匹配

  • 最大匹配即每一个都匹配上min（u， v）。
  • 贪心算法可能导致，有些节点未匹配上
  • 可以添加起始节点以及终止节点，使用网络流算法进行求解。

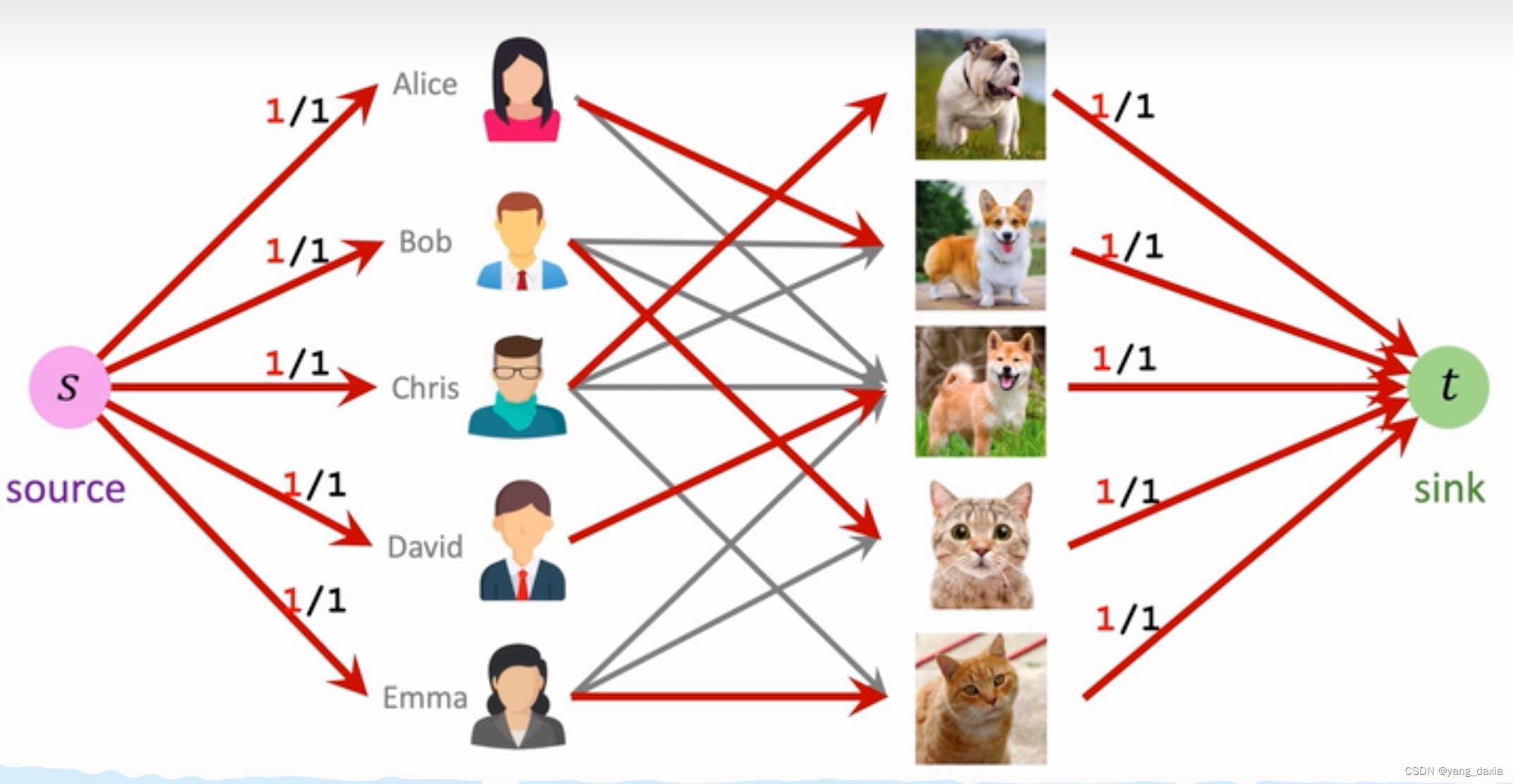
在这里插入图片描述

有权二部图中的最大匹配Maximum-Weight Bipartite Matching

  • 每一条边都有权重，最大匹配追求的是整体的权重和最大。（整体收益最大）
  • 最大匹配可以转化为最小匹配算法。即把权重*-1, 最小匹配的结果就是最大匹配的结果。
  • 匈牙利算法可以解决最小匹配问题，但是u和v的节点数量需要保持一致，算法复杂度为O(n^3),暴力为O(n!)

匈牙利算法

  • 构建u*u矩阵，没有边的为0

  • 每一行减去每一行的最小值
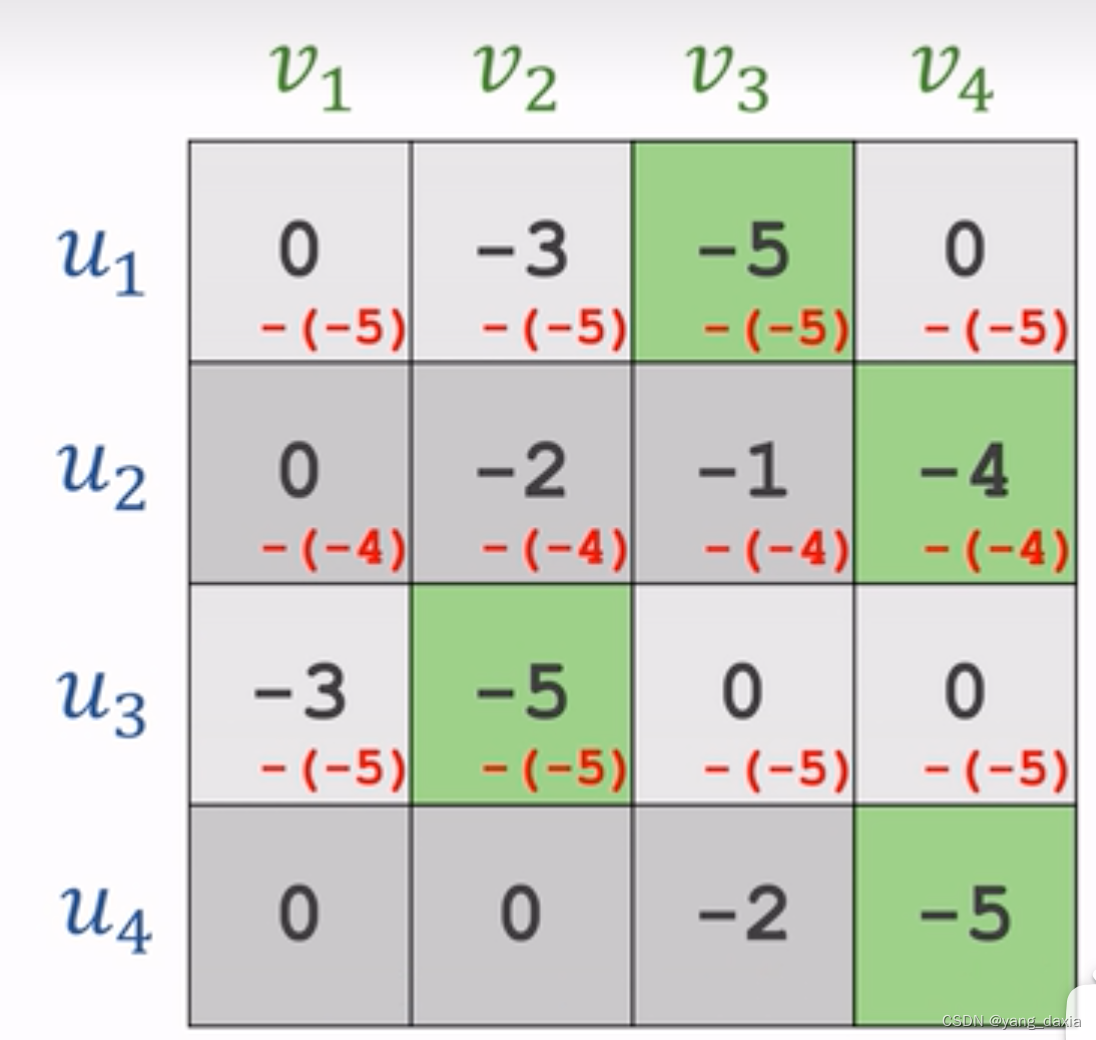
    在这里插入图片描述

  • 每一列减去每一列的最小值
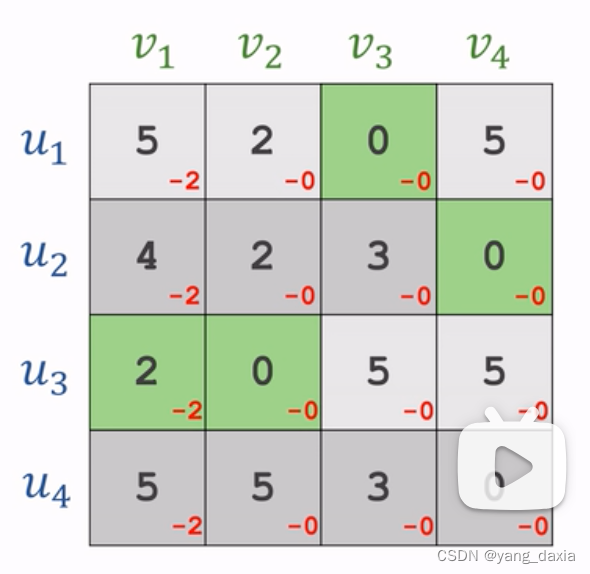
    在这里插入图片描述

  • 使用最小的线覆盖所有的0。如果线的数量小于u的数量，则剩下的继续找最小元素，然后递减，节点处加上该元素；如果数量相同，则优先找唯一有0的点进行匹配。
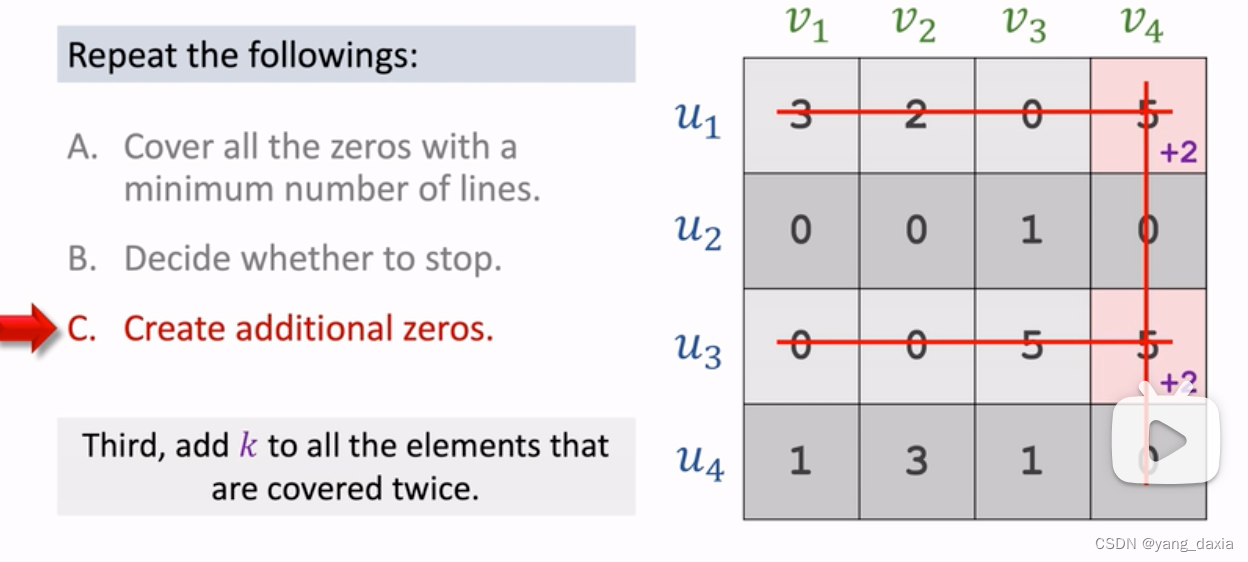
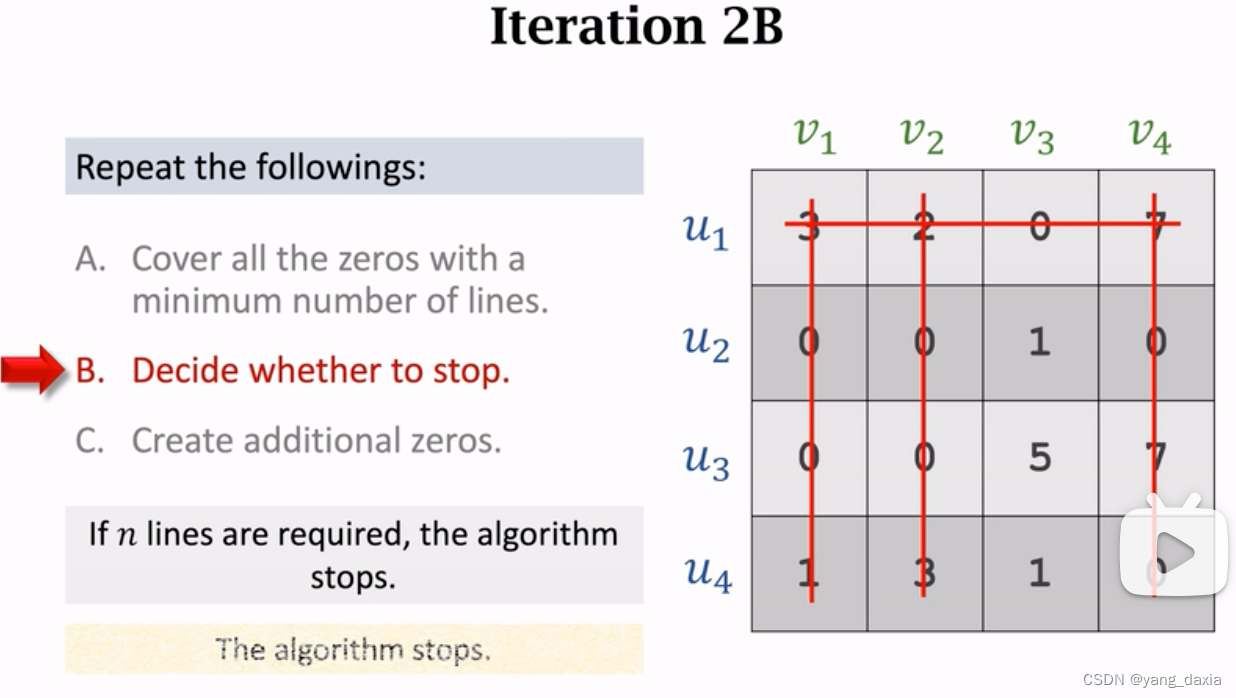
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述
    在这里插入图片描述

  • 最大匹配结果可能不止1中，如5，2，3和5， 0， 5都是15。
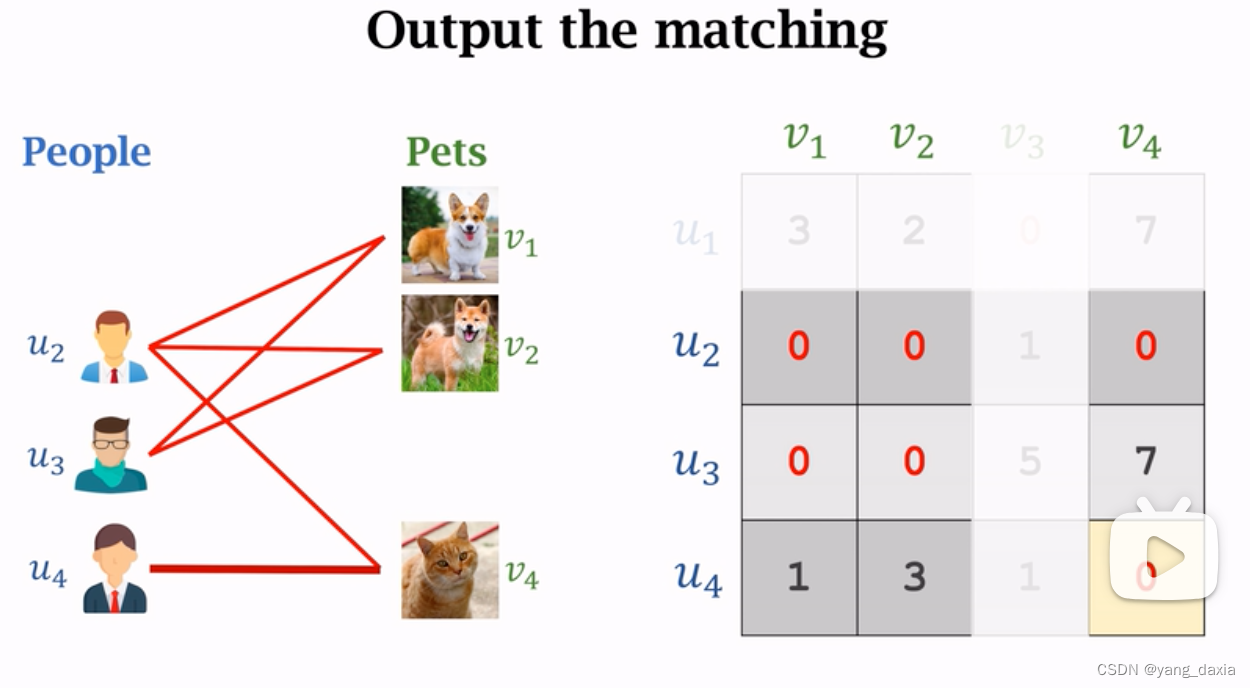
    在这里插入图片描述

在这里插入图片描述

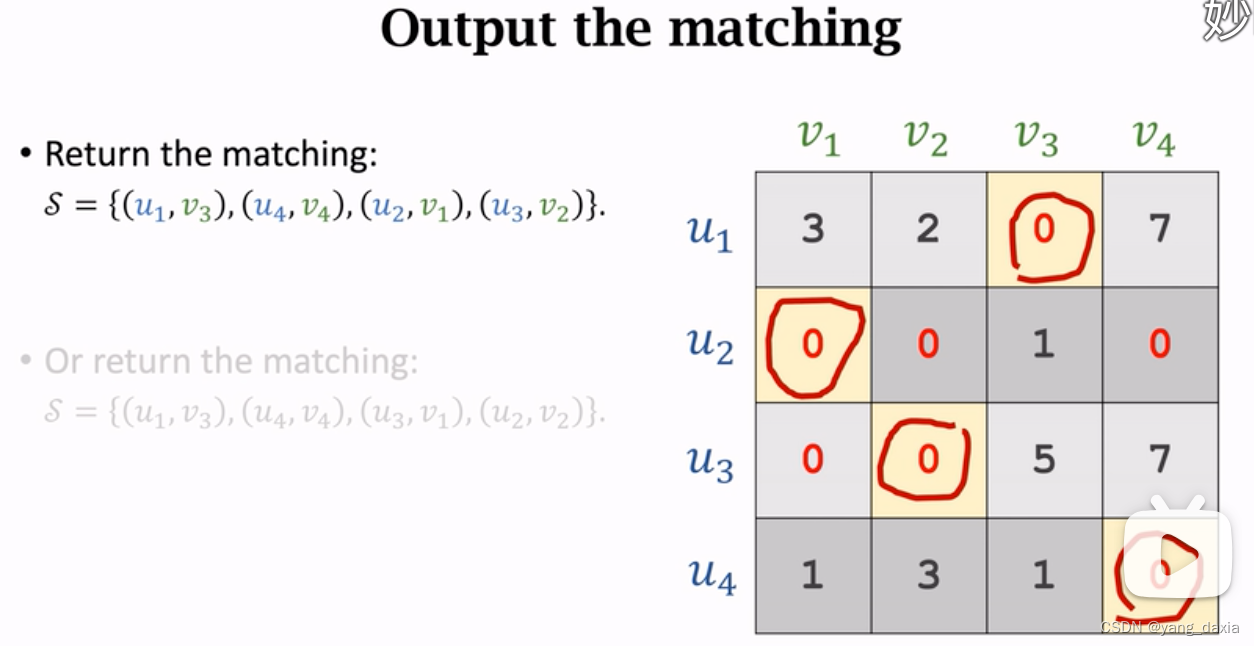
  • 如果uv节点不一致，可以通过补几个虚拟节点，权重设置为0，使得uv节点数量一致，那就可以用匈牙利算法求解了。

稳定婚配算法

  • 一种特殊的2分图匹配问题
  • 边由权重变成了顺序，而且是双向的
  • 可以用gale-shapely算法求解
  • 时间复杂度为O(n^2)

代码实现

  • 通过找增广路径的方式进行求解
  • 非匹配点出发，到非匹配点截至，中间为非匹配与匹配交替出现，然后变换状态即可。
  • KM算法是加了权重的匈牙利算法，先把左边赋值最大权重，然后如果冲突，左边-detla, 右边+detla的操作，再通过增广路径求解。detla为lx+ly-weight
    https://blog.csdn.net/sidnee/article/details/106298615

https://blog.csdn.net/qq_37457202/article/details/80161274

参考：
https://www.bilibili.com/video/BV1G54y157HA/?spm_id_from=333.788&vd_source=d141bc07699831d8053b781fd6944d5f

相关文章：

2分图匹配算法

定义 节点u直接无边，v之间无边，边只存在uv之间。判断方法：BFS染色法，全部染色后，相邻边不同色 无权二部图中的最大匹配 最大匹配即每一个都匹配上min（u， v）。贪心算法可能导致&…...

编程日记 2023/12/5 2:03:19

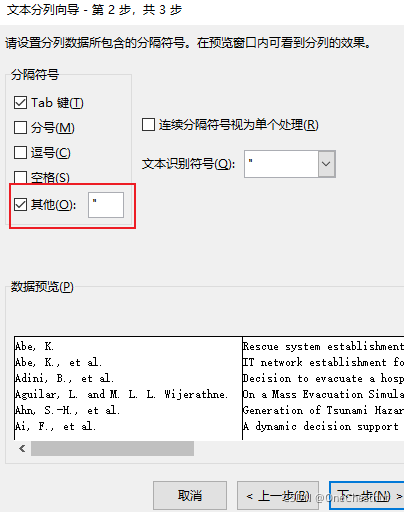
[EndNote学习笔记] 导出库中文献的作者、标题、年份到Excel

菜单栏Edit中，选择 Output Styles 在默认的 Annotated上进行修改，在Bibliography栏下的Templates中修改想要导出的格式 其中，每个粗体标题表示，针对不同的文献类型，设置相应的导出格式。一般为Journal Article&…...

编程日记 2023/12/5 2:02:17

SQL Sever 基础知识 - 数据查询

SQL Sever 基础知识 - 一、查询数据 一、查询数据第1节 基本 SQL Server 语句SELECT第2节 SELECT语句示例2.1 SELECT - 检索表示例的某些列2.2 SELECT - 检索表的所有列2.3 SELECT - 对结果集进行筛选2.4 SELECT - 对结果集进行排序2.5 SELECT - 对结果集进行分组2.5 SELECT - …...

编程日记 2023/12/5 2:00:15

Vue入门——v-on标签

文章目录 规则v-on 一、案例总结 规则 v-on 作用&#xff1a;为html标签绑定事件语法&#xff1a; v-on&#xff1a;事件名&#xff1a;“函数名”简写为 事件名“函数名” 注意&#xff1a;函数需要定义在methods选项内部 一、案例 我们给案件绑定一个单击事件 <!DOCTYPE…...

编程日记 2023/12/5 1:55:06

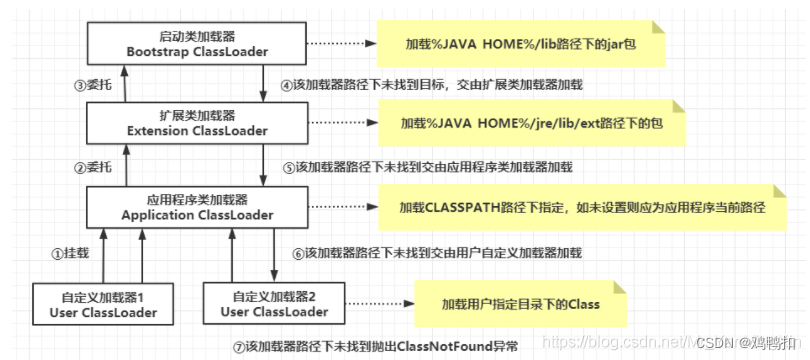
JVM：双亲委派（未完结）

类加载 定义 一个java文件从编写代码到最终运行&#xff0c;必须要经历编译和类加载的过程&#xff0c;如下图&#xff08;图源自b站视频up主“跟着Mic学架构”&#xff09;。 编译就是把.java文件变成.class文件。类加载就是把.class文件加载到JVM内存中&#xff0c;得到一…...

编程日记 2023/12/5 1:54:05

Leetcode 2661. 找出叠涂元素

Leetcode 2661. 找出叠涂元素题目 给你一个下标从 0 开始的整数数组 arr 和一个 m x n 的整数 矩阵 mat 。arr 和 mat 都包含范围 [1&#xff0c;m * n] 内的 所有 整数。从下标 0 开始遍历 arr 中的每个下标 i &#xff0c;并将包含整数 arr[i] 的 mat 单元格涂色。请你找出 a…...

编程日记 2023/12/5 1:53:03

vscode代码调试配置

C/C代码调试 点击 vscode左侧的 run and debug&#xff0c;新建launch.json 和 tasks.json&#xff0c;并进行配置如下 launch.json {// Use IntelliSense to learn about possible attributes.// Hover to view descriptions of existing attributes.// For more informati…...

编程日记 2023/12/5 1:47:56

PTA 7-225 sdut-C语言实验- 冒泡排序中数据交换的次数

听说过冒泡排序么&#xff1f;一种很暴力的排序方法。今天我们不希望你用它来排序&#xff0c;而是希望你能算出从小到大冒泡排序的过程中一共进行了多少次数据交换。 输入格式: 输入数据的第一行为一个正整数 T &#xff0c;表示有 T 组测试数据。 接下来T行&#xff0c;每行…...

编程日记 2023/12/5 1:46:55

新的 BLUFFS 攻击导致蓝牙连接不再私密

蓝牙是一种连接我们设备的低功耗无线技术&#xff0c;有一个新的漏洞需要解决。 中间的攻击者可以使用新的 BLUFFS 攻击轻松窥探您的通信。 法国研究中心 EURECOM 的研究员 Daniele Antonioli 演示了六种新颖的攻击&#xff0c;这些攻击被定义为 BLUFFS&#xff08;蓝牙转发和…...

编程日记 2023/12/5 1:45:54

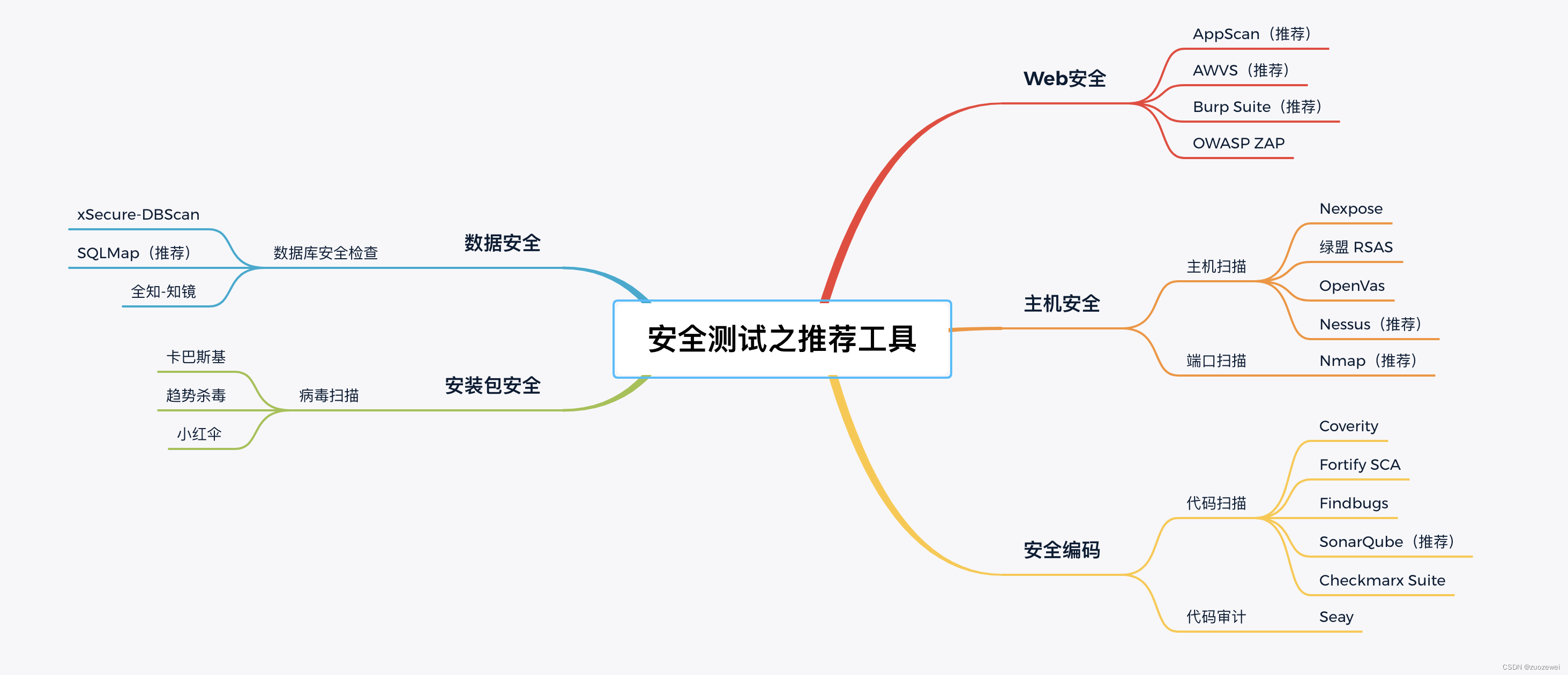
安全测试之推荐工具（一）

文章目录 一、前言二、Web安全&#xff08;一&#xff09;AppScan&#xff08;推荐&#xff09;&#xff08;二&#xff09;AWVS&#xff08;推荐&#xff09;&#xff08;三&#xff09;Burp Suite&#xff08;推荐&#xff09;&#xff08;四&#xff09;OWASP ZAP 三、主机安…...

编程日记 2023/12/5 1:42:50

final关键字

修饰 类&#xff0c;属性&#xff0c;方法&#xff0c;局部变量&#xff08;包括方法参数&#xff09; 类似c语言的const 使用方式&#xff1a; 1 不希望类被继承 用final类&#xff08;类很重要&#xff0c;担心别人重写/修改&#xff09; 2 不希望某…...

编程日记 2023/12/5 1:40:48

WPF MVVM模式下如何将UI窗口变量传参到Viewmodel层

WPF MVVM模式下如何将UI窗口变量传参到Viewmodel层 UI层窗口定义 //窗口中绑定ViewModel<hc:GlowWindow.DataContext><viewmodel:MainWindowViewModel /></hc:GlowWindow.DataContext>//注册初始化事件<hc:Interaction.Triggers><hc:EventTrigger…...

编程日记 2023/12/5 1:39:45

条款22：将成员变量声明为private

1.前言 首先&#xff0c;我们应该利用反证法&#xff0c;看看为什么成员变量不该是public&#xff0c;然后再了解所有反对public成员变量的论点同样适用于protected成员变量。最后得出一个结论&#xff1a;成员变量应该是private。 2.为什么不用public 如果成员变量不是publ…...

编程日记 2023/12/5 1:38:44

PTA 7-224 sdut-C语言实验-排序问题

输入10个整数&#xff0c;将它们从小到大排序后输出&#xff0c;并给出现在每个元素在原来序列中的位置。 输入格式: 输入数据有一行&#xff0c;包含10个整数&#xff0c;用空格分开。 输出格式: 输出数据有两行&#xff0c;第一行为排序后的序列&#xff0c;第二行为排序…...

编程日记 2023/12/5 1:34:38

【JavaScript】3.2 JavaScript性能优化

文章目录 1. 避免全局查找2. 避免不必要的属性查找3. 使用快速的JavaScript方法4. 避免不必要的DOM操作5. 使用Web Workers进行后台处理总结 性能优化是任何编程语言的重要组成部分&#xff0c;JavaScript也不例外。在这个章节中&#xff0c;我们将探讨如何优化JavaScript代码&…...

编程日记 2023/12/5 1:33:37

pytorch bert实现文本分类

以imdb公开数据集为例&#xff0c;bert模型可以在huggingface上自行挑选 1.导入必要的库 import os import torch from torch.utils.data import DataLoader, TensorDataset, random_split from transformers import BertTokenizer, BertModel, BertConfig from torch import…...

编程日记 2023/12/5 1:31:32

《开箱元宇宙》：Madballs 解锁炫酷新境界，人物化身系列大卖

你是否曾想过&#xff0c;元宇宙是如何融入世界上最具代表性的品牌和名人的战略中的&#xff1f;在本期的《开箱元宇宙》 系列中&#xff0c;我们与 Madballs 的战略顾问 Derek Roberto 一起聊聊 Madballs 如何在 90 分钟内售罄 2,000 个人物化身系列&#xff0c;以及是什么原…...

编程日记 2023/12/5 1:30:31

4K-Resolution Photo Exposure Correction at 125 FPS with ~8K Parameters

MSLTNet开源 | 4K分辨率125FPS8K的参数量&#xff0c;怎养才可以拒绝这样的模型呢&#xff1f; 错误的曝光照片的校正已经被广泛使用深度卷积神经网络或Transformer进行广泛修正。尽管这些方法具有令人鼓舞的表现&#xff0c;但它们通常在高分辨率照片上具有大量的参数数量和沉…...

编程日记 2023/12/5 1:27:28

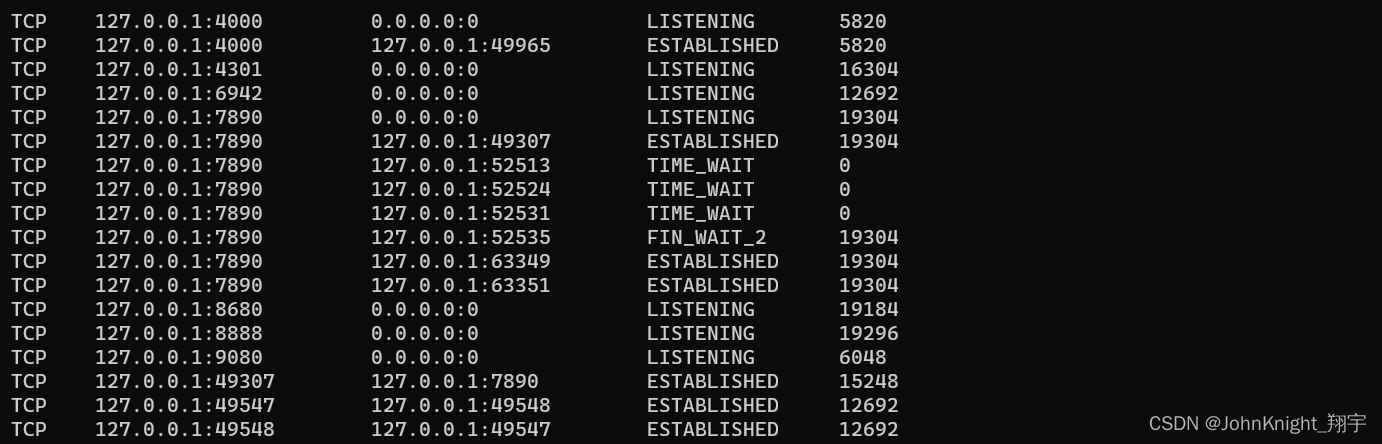
网络初识：局域网广域网网络通信基础

提示&#xff1a;文章写完后&#xff0c;目录可以自动生成&#xff0c;如何生成可参考右边的帮助文档 文章目录 前言一、局域网LAN是什么&#xff1f;二、广域网是什么&#xff1a;三. IP地址四.端口号五.认识协议5.1五元组 总结 前言 一、局域网LAN是什么&#xff1f; 局域网…...

编程日记 2023/12/5 1:26:27

JVM之jps虚拟机进程状态工具

jps虚拟机进程状态工具 1、jps jps&#xff1a;(JVM Process Status Tool)&#xff0c;虚拟机进程状态工具&#xff0c;可以列出正在运行的虚拟机进程&#xff0c;并显示虚拟机执 行主类&#xff08;Main Class&#xff0c;main()函数所在的类&#xff09;的名称&#xff0c…...

编程日记 2023/12/5 1:24:23

C++实现顺序栈的基本操作（扩展）

#include <stdio.h> typedef char ElemType; #define StackSize 100 /*顺序栈的初始分配空间*/ typedef struct { ElemType data[StackSize]; /*保存栈中元素*/int top; /*栈顶指针*/ } SqStack; void InitStack(SqStack &st) {st.top-1; } …...

编程日记 2023/12/5 1:23:22

用python写一个简单的爬虫

爬虫是一种自动化程序&#xff0c;用于从互联网上获取数据。它能够模拟人类浏览网页的行为&#xff0c;访问网页并提取所需的信息。爬虫在很多领域都有广泛的应用&#xff0c;例如数据采集、信息监控、搜索引擎索引等。 下面是一个使用Python编写的简单爬虫示例&#xff1a; …...

编程日记 2023/12/5 1:22:20

分布式追踪

目录 文章目录 目录自定义指标1.删除标签2.添加指标3.禁用指标 分布式追踪上下文传递Jaeger 关于我最后最后 自定义指标 除了 Istio 自带的指标外&#xff0c;我们还可以自定义指标&#xff0c;要自定指标需要用到 Istio 提供的 Telemetry API&#xff0c;该 API 能够灵活地配…...

编程日记 2023/12/5 1:21:19

make -c VS make -f

make 是一个用于构建&#xff08;编译&#xff09;项目的工具&#xff0c;它通过读取一个名为 Makefile 的文件来执行构建任务。make 命令有很多选项和参数&#xff0c;其中包括 -c 和 -f。 make -c&#xff1a; 作用&#xff1a;指定进入指定的目录并执行相应的 Makefile。 示…...

编程日记 2023/12/5 1:20:17

Unity 代码控制Color无变化

Unity中&#xff0c;我们给Color的赋值比较常用的方法是&#xff1a; 1、使用预定义颜色常量&#xff1a; Color color Color.white; //白色 Color color Color.black; //黑色 Color color Color.red; //红色 Color color Color.green; //绿色 Color color Color.blue; …...

编程日记 2023/12/5 1:19:16

【Erlang进阶学习】2、匿名函数

受到其它一些函数式编程开发语言的影响&#xff0c;在Erlang语言中&#xff0c;将函数作为一个对象&#xff0c;赋予其“变量”的属性&#xff0c;即为我们的匿名函数 或 简称 fun&#xff0c;它具有以下特性&#xff1a; &#xff08;匿名函数&#xff1a;不是定义在Erlang模…...

编程日记 2023/12/5 1:18:15

肖sir__mysql之视图__009

mysql之视图 一、什么是视图 视图是一个虚拟表&#xff08;逻辑表&#xff09;&#xff0c;它不在数据库中以存储形式保存&#xff08;本身包含数据&#xff09;&#xff0c;是在使用视图的时候动态生成。 二、视图作用 1、查询数据库中的非常复的数据 例如&#xff1a;多表&a…...

编程日记 2023/12/5 1:17:13

FPGA falsh相关知识总结

1.存储容量是128M/8 Mb16MB 2.有256个sector扇区*每个扇区64KB16MB 3.一页256Byte 4.页编程地址0256 5&#xff1a;在调试SPI时序的时候一定注意&#xff0c;miso和mosi两个管脚只要没发送数据就一定要悬空&#xff08;处于高组态&#xff09;&#xff0c;不然指令会通过两…...

编程日记 2023/12/5 1:16:11

升辉清洁IPO：广东清洁服务“一哥”还需要讲好全国化的故事

近日&#xff0c;广东物业清洁服务“一哥”升辉清洁第四次冲击IPO成功&#xff0c;拟于12月5日在香港主板挂牌上市。自2021年4月第一次递交招股书&#xff0c;时隔两年半&#xff0c;升辉清洁终于拿到了上市的门票。 天眼查显示&#xff0c;升辉清洁成立于2000年&#xff0c;主…...

编程日记 2023/12/5 1:15:10

Python自动化办公：PDF文件的分割与合并

我们平时办公中&#xff0c;可能需要对pdf进行合并或者分割&#xff0c;但奈何没有可以白嫖的工具&#xff0c;此时python就是一个万能工具库。 其中PyPDF2是一个用于处理PDF文件的Python库&#xff0c;它提供了分割和合并PDF文件的功能。 在本篇博客中&#xff0c;我们将详细…...

编程日记 2023/12/5 1:13:09

使用云主机做网站教程/网站优化网站优化

SpringMVC_requestMapping 项目搭建见上篇《初识 Spring(09)---(搭建SpringMVC项目&#xff09;》 1.requestMapping既可以用在方法上&#xff0c;也可以用在类上 文件目录&#xff1a; 代码&#xff1a;新建SpringmvcTest.java package com.neuedu.springmvc.controller;i…...

编程日记 2024/11/19 23:10:54

怎么做网站外链接/最新百度快速排名技术

技术特征&#xff1a;1.一种基于树状结构的测试用例管理方法&#xff0c;其特征在于&#xff1a;所述的方法包括&#xff1a;获取测试用例文件&#xff1b;获取数据存储策略和数据存储空间&#xff1b;读取所述测试用例文件&#xff0c;以建立节点树&#xff0c;并根据所述数据…...

编程日记 2024/11/19 22:36:26

怎么看个人做的付费视频网站/深圳seo云哥

目录 正则表达式语法规则 字符 预定义字符集 数量词 贪婪和非贪婪 边界匹配&#xff08;不消耗匹配字符串中的字符) 逻辑、分组 Python re模块介绍 引入模块 正则检索 正则分割字符串 字符串替换 分组引用 匹配中文 正则表达式语法规则 百度百科简介&#xff1a…...

编程日记 2024/11/19 22:26:20

南京企业网站设计建设/做网上营销怎样推广

/*第一种方法 require&#xff1a;缺点就是如果加载文件过多&#xff0c;需要多个require*/// require(A.CLASS.PHP);// require(B.CLASS.PHP);/*第二种方法__autoloadPHP5在new 一个没有存在的类&#xff0c;会自动调用这个__autoload函数,____autoload只是去include_path寻找…...

编程日记 2024/11/19 22:15:10

福州建网站 做网页/2345纯净版推广包

已同步到个人博客&#xff0c;欢迎访问。 总结 最常用的判断方法是Object.prototype.slice.call()&#xff0c;其他判断的方法都有着各种问题&#xff1a; Array.isArray判断数组&#xff0c;需要ES6的支持typeof有各种特殊情况instanceof对于字面量不适用&#xff0c;并且在…...

编程日记 2024/11/19 20:00:00

房屋租赁网站开发模版/百度资源站长平台

windows下boost库的基本使用方法 因为boost都是使用模板的技术&#xff0c;所以所有代码都是写在一个.hpp头文件中。这样boost中的大部分内容是不需要编译生成相应的链接库&#xff0c;只需要设置下面的包含目录&#xff08;或者设置一下环境变量&#xff09;&#xff0c;在源文…...

编程日记 2024/11/19 18:42:49