C++ day53 最长公共子序列 不相交的线 最大子序和
题目1:1143 最长公共子序列
题目链接:最长公共子序列
对题目的理解
返回两个字符串的最长公共子序列的长度,如果不存在公共子序列,返回0,注意返回的是最长公共子序列,与前一天的最后一道题不同的是子序列是可以不连续的
动态规划
动规五部曲
1)dp数组及下标i的含义
dp[i][j]:以[0,i-1]的nums1和以[0,j-1]的nums2的最长公共子序列的长度
2)递推公式
主要是两种情况,1)元素相同;2)元素不同
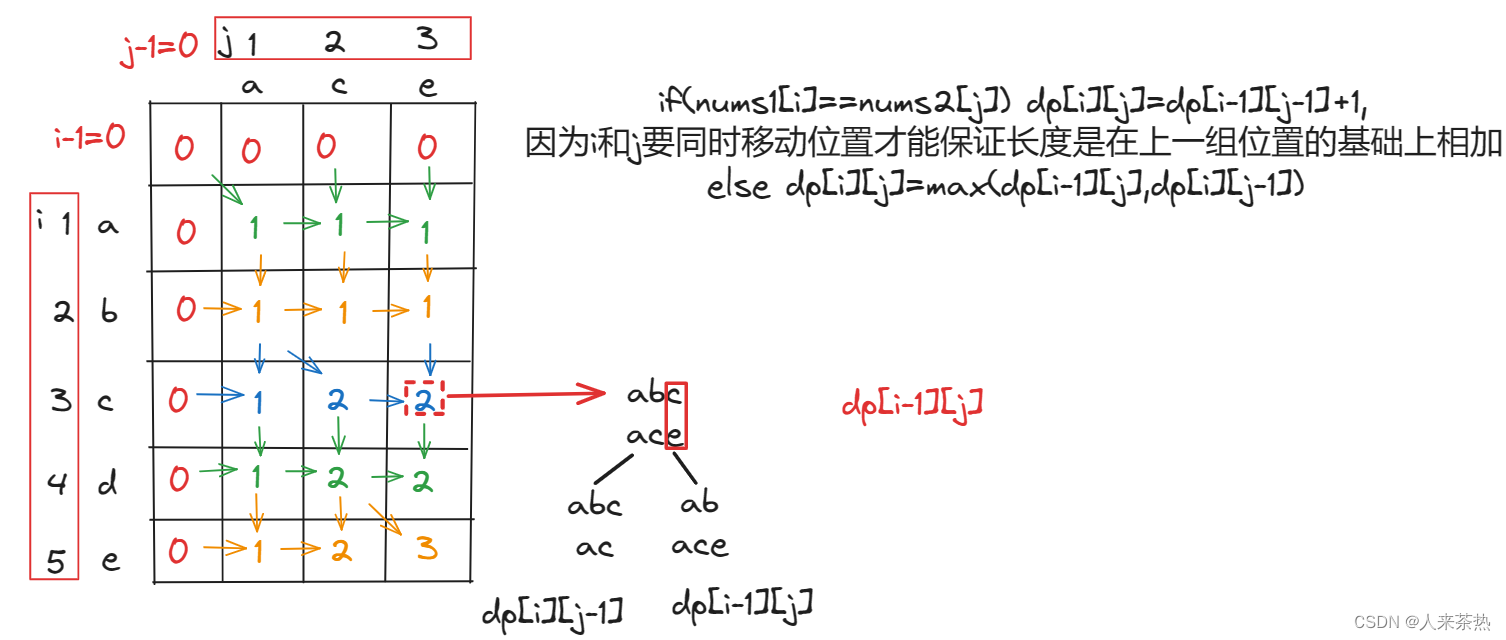
3)dp数组初始化

dp[i][0]和dp[0][j] 无意义,但是为了递推公式的需要,均初始化为0,其余下标位置处的数值初始化为任意值均可,但是为了方便起见,均初始化为0。
4)遍历顺序
根据递推公式,由左往右推导遍历,从上到下推导遍历。
5)打印dp数组
最终结果在dp[num1.size()][nums2.size()]
代码
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {//定义并初始化dp数组vector<vector<int>> dp(text1.size()+1,vector<int>(text2.size()+1,0));for(int i=1;i<=text1.size();i++){for(int j=1;j<=text2.size();j++){if(text1[i-1]==text2[j-1]) dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}return dp[text1.size()][text2.size()];}
};- 时间复杂度: O(n * m),其中 n 和 m 分别为 text1 和 text2 的长度
- 空间复杂度: O(n * m)
题目2:1035 不相交的线
题目链接:不相交的线
对题目的理解
连接数组nums1和nums2中的相同数字代表的点,每条直线不能相交,计算最大连线数
直线不能相交,这就是说明在字符串A中找到一个与字符串B相同的子序列,且这个子序列不能改变相对顺序,只要相对顺序不改变,连接相同数字的直线就不会相交。
本题就是套了一层连线的外壳,代码与上一道题一模一样,就是找两个数组中存在的最大相同子序列的长度。
分析过程与上一道题一模一样
代码
class Solution {
public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {//定义并初始化dp数组vector<vector<int>> dp(nums1.size()+1,vector<int>(nums2.size()+1,0));for(int i=1;i<=nums1.size();i++){for(int j=1;j<=nums2.size();j++){if(nums1[i-1]==nums2[j-1]) dp[i][j]=dp[i-1][j-1]+1;else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}return dp[nums1.size()][nums2.size()];}
};- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
题目3:53 最大子序和
题目链接:最大子序和
对题目的理解
找出具有最大和的连续子数组(至少包含一个元素),返回最大和,注意子数组是连续的
贪心算法
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小;全局最优:选取最大“连续和”
不断调整最大子序和区间的起始位置,只要连续和还是正数就会对后面的元素起到增大总和的作用。 所以只要连续和为正数就保留。
代码
class Solution {
public:int maxSubArray(vector<int>& nums) {int count=0;//记录连续和int result = INT_MIN;//记录最大连续和for(int i=0;i<nums.size();i++){count += nums[i];if(count>result) result = count;if(count<0) count = 0;//连续和为负数,重新计算连续和}return result;}
};- 时间复杂度:O(n)
- 空间复杂度:O(1)
动态规划
动规五部曲
1)dp数组及下标i的含义
dp[i]:以nums[i]结尾(包括nums[i])的最大连续子序列的和
2)递推公式
dp[i]可以从两个方向推导出来
1)延续前面的和:dp[i]=dp[i-1]+nums[i]
2)从nums[i]重新计算:dp[i]=nums[i]
dp[i]=max(dp[i-1]+nums[i],nums[i])
3)dp数组初始化
根据递推公式,dp[i]依赖于dp[i-1] 源头是dp[0],根据dp数组定义,dp[0]=nums[0]
非0下标的dp数组,可以初始化为任意值,因为可以在后续计算中被覆盖,但是为了初始化方便,统一初始为nums[0]
4)遍历顺序
根据递推公式,dp[i]依赖于dp[i-1],从前往后遍历
for(i=1;i<nums.size();i++) 注意i从1开始遍历
5)打印dp数组
根据dp数组定义,最终结果不一定是dp[nums[i]-1],应该找每一个i为终点的连续最大子序列,需要把所有结果遍历一遍,求得最大值
代码
class Solution {
public:int maxSubArray(vector<int>& nums) {//定义并初始化dp数组vector<int> dp(nums.size(),nums[0]);int result = INT_MIN;for(int i=1;i<nums.size();i++){dp[i]=max(dp[i-1]+nums[i],nums[i]);cout<<dp[i]<<endl;result = max(result,dp[i]);}return result;}
};上述代码会出现如下的案例错误
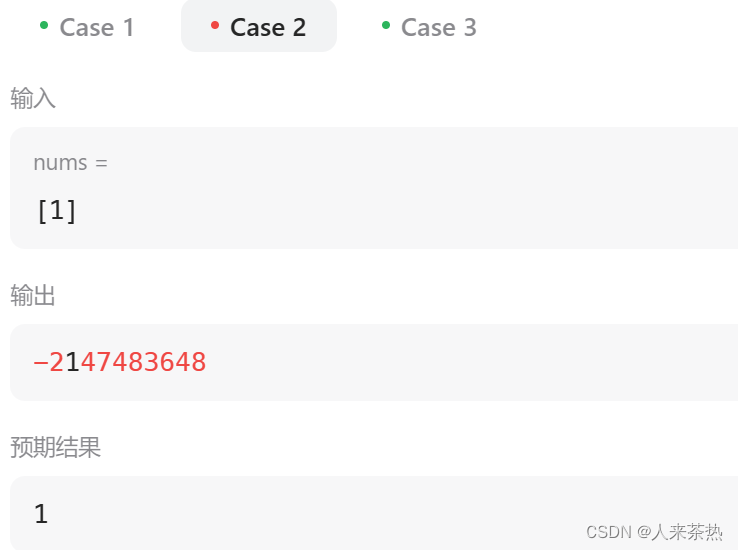
错误的原因在于:result初始化为最小值,而for循环中计算的是dp[1],就是max(dp[0]+nums[1],nums[1]),是从数组中的第二个元素开始考虑的,如果这样的话,对于只有一个元素的数组根本就没有经过for循环,直接输出了result,所有result不能这样初始化,应该初始化为nums[0],即初始化为数组的第1个元素值,这样才能在数组只有1个元素的情况下,result考虑到第一个元素。
代码改正如下:
class Solution {
public:int maxSubArray(vector<int>& nums) {//定义并初始化dp数组vector<int> dp(nums.size(),nums[0]);int result = nums[0];for(int i=1;i<nums.size();i++){dp[i]=max(dp[i-1]+nums[i],nums[i]);cout<<dp[i]<<endl;result = max(result,dp[i]);}return result;}
};- 时间复杂度:O(n)
- 空间复杂度:O(n)
相关文章:

C++ day53 最长公共子序列 不相交的线 最大子序和
题目1:1143 最长公共子序列 题目链接:最长公共子序列 对题目的理解 返回两个字符串的最长公共子序列的长度,如果不存在公共子序列,返回0,注意返回的是最长公共子序列,与前一天的最后一道题不同的是子序…...

ubuntu中删除镜像和容器、ubuntu20.04配置静态ip
1 删除镜像 # 短id sudo docker rmi 镜像id # 完整id sudo docker rmi 镜像id# 镜像名【REPOSITORY:TAG】 sudo docker rmi redis:latest2 删除容器 # 删除某个具体容器 sudo docker rm 容器id# 删除Exited状态/未运行的容器,三种命令均可 sudo docker rm docker …...

华为手环 8 五款免费表盘已上线,请注意查收
华为手环 8,作为一款集时尚与实用于一体的智能手环,不仅具备强大的功能,还经常更新的表盘样式,让用户掌控时间与健康的同时,也能展现自己的时尚品味。这不,12 月官方免费表盘又上新了,推出了五款…...

JOSEF约瑟 同步检查继电器DT-13/200 100V柜内安装,板前接线
系列型号 DT-13/200同步检查继电器; DT-13/160同步检查继电器; DT-13/130同步检查继电器; DT-13/120同步检查继电器; DT-13/90同步检查继电器; DT-13/254同步检查继电器; 同步检查继电器DT-13/200 100V柜内板前接线 一、用途 DT-13型同步检查继电器用于两端供电线路的…...

龙迅#LT8311X3 USB中继器应用描述!
1. 概述 LT8311X3是一款USB 2.0高速信号中继器,用于补偿ISI引起的高速信号衰减。通过外部下拉电阻器选择的编程补偿增益有助于提高 USB 2.0 高速信号质量并通过 CTS 测试。 2. 特点 • 兼容 USB 2.0、OTG 2.0 和 BC 1.2• 支持 HS、FS、LS 信令 • 自动检测和补偿 U…...

eclipse jee中 如何建立动态网页及服务的设置问题
第一次打开eclipse 时,设置工作区时,一定是空目录 进入后 File-----NEW------Dynamic Web Project 填 项目名,不要有大写 m1 next next Generate前面打对勾 finish 第一大步: window----Preferences type filter text 处填 :Serve…...
一张网页截图,AI帮你写前端代码,前端窃喜,终于不用干体力活了
简介 众所周知,作为一个前端开发来说,尤其是比较偏营销和页面频繁改版的项目,大部分的时间都在”套模板“,根本没有精力学习前端技术,那么这个项目可谓是让前端的小伙伴们看到了一丝丝的曙光。将屏幕截图转换为代码&a…...

处理k8s中创建ingress失败
创建ingress: 如果在创建过程中出错了: 处理方法就是: kubectl get ValidatingWebhookConfiguration kubectl delete -A ValidatingWebhookConfiguration ingress-nginx-admission 然后再次创建,发现可以:...
Redis高可用集群架构
高可用集群架构 哨兵模式缺点 主从切换阶段, redis服务不可用,高可用不太友好只有单个主节点对外服务,不能支持高并发单节点如果设置内存过大,导致持久化文件很大,影响数据恢复,主从同步性能 高可用集群…...

JAVA常见问题解答:解决Java 11新特性兼容性问题的六个步骤
引言: 随着技术的不断发展,Java作为一种被广泛使用的编程语言,也在不断更新和改进。Java 11作为Java的最新版本,带来了许多新的特性和改进。然而,对于一些老旧的Java应用程序来说,升级到Java 11可能会带来一…...
【C语言】深入理解指针(1)
目录 前言 (一)内存与地址 从实际生活出发 地址 内存 内存与地址关系密切 (二)指针变量 指针变量与取地址操作符 指针变量与解引用操作符 指针的大小 指针的运算 指针 - 整数 指针-指针 指针的关系运算 指针的类型的…...
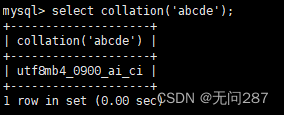
MySQL的系统信息函数
系统信息函数让你更好的使用MySQL数据库 1、version()函数 查看MySQL系统版本信息号 select version();2、connection_id()函数 查看当前登入用户的连接次数 直接调用CONNECTION_ID()函数--不需任何参数--就可以看到当下连接MySQL服务器的连接次数,不同时间段该…...
 方法)
python中.format() 方法
.format() 方法是一种用于格式化字符串的方法,它允许将变量的值插入到字符串中的占位符位置上。该方法可以接受一个或多个参数,并根据给定的格式规则将它们插入到字符串中。 下面是一些使用 .format() 方法的示例: # 基本用法 name "…...
【新手解答8】深入探索 C 语言:递归与循环的应用
C语言的相关问题解答 写在最前面问题:探索递归与循环在C语言中的应用解析现有代码分析整合循环示例代码修改注意事项结论 延伸:递归和循环的退出条件设置解析使用递归使用循环选择适合的方法 写在最前面 一位粉丝私信交流,回想起了当初的我C…...
服务器中深度学习环境的配置
安装流程 11.17 日,周末去高校参加学术会议,起因, 由于使用了某高校内的公共有线网络, 远程连接服务器后,黑客利用 ssh 开放的 22 端口, 篡改了主机的配置, 使得只要一连上网络, 服…...

html实现各种好看的鼠标滑过图片特效模板
文章目录 1.鼠标悬浮效果1.1 渐动效果1.2 渐变效果1.3 边框效果1.4 线行效果1.5 图标效果1.6 块状效果1.7 边线效果1.8 放大效果1.9 渐出效果1.10 痕迹效果1.11 交叉效果1.12 着重效果1.13 详展效果1.14 能动效果1.15 明细效果 2.主要源码2.1 源代码 源码下载 作者:…...
leetcode:LCR 122. 路径加密python3解法)
难度:简单 假定一段路径记作字符串 path,其中以 "." 作为分隔符。现需将路径加密,加密方法为将 path 中的分隔符替换为空格 " ",请返回加密后的字符串。 示例 1: 输入:path "a.a…...
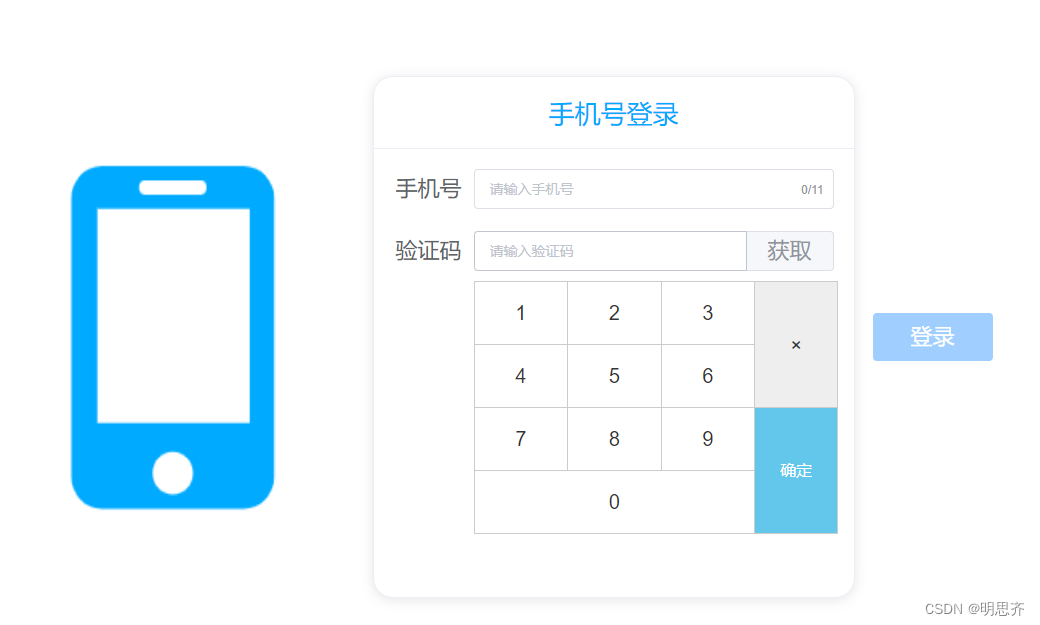
vue中实现纯数字键盘
一、完整 代码展示 <template><div class"login"><div class"login-content"><img class"img" src"../../assets/image/loginPhone.png" /><el-card class"box-card"><div slot"hea…...
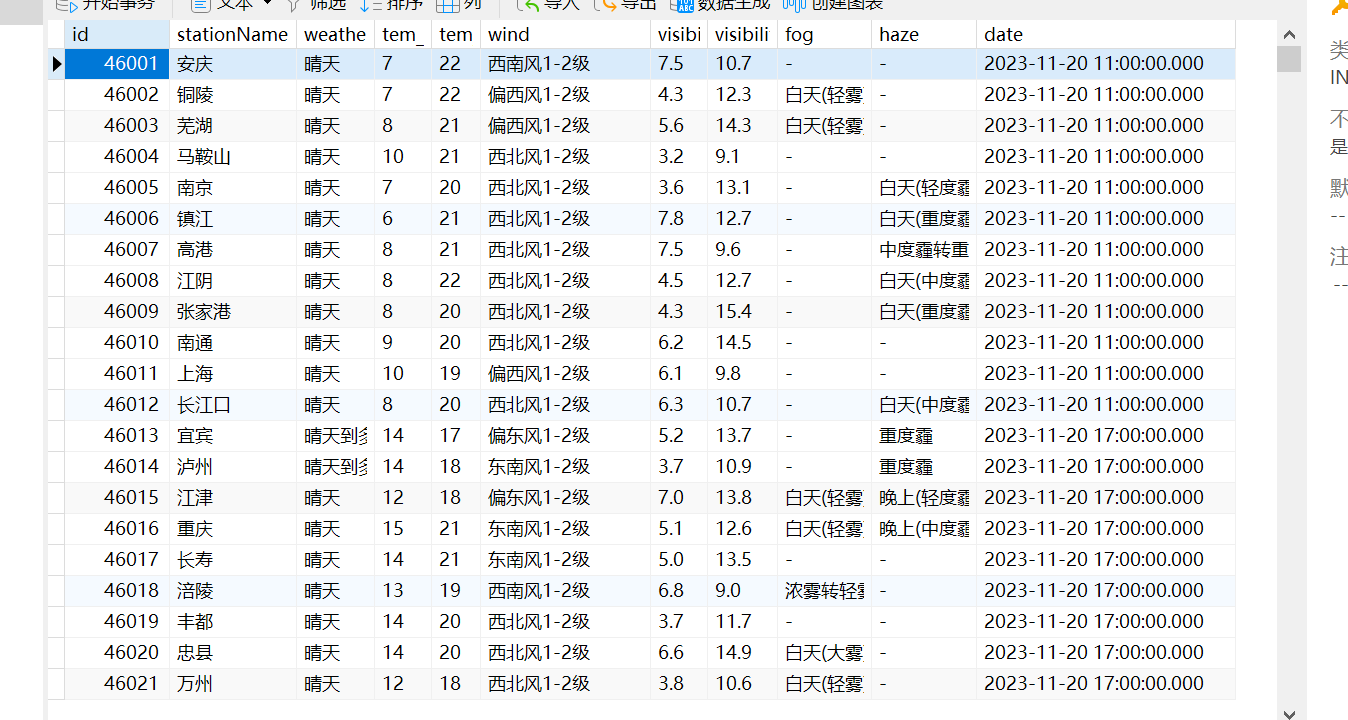
C#简化工作之实现网页爬虫获取数据
1、需求 想要获取网站上所有的气象信息,网站如下所示: 目前总共有67页,随便点开一个如下所示: 需要获取所有天气数据,如果靠一个个点开再一个个复制粘贴那么也不知道什么时候才能完成,这个时候就可以使用C…...

回顾过去的五年
回顾过去的五年 不知不觉,一晃就5年了。孩子也慢慢的长大了,都快和我一样高了。 2017-2019年依旧服务于原公司。后来公司停业了,得到了相应的赔偿。在家里呆了几个月,变成了无业游民。陪伴家人,也会收到家人的鞭策。…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

宇树科技,改名了!
提到国内具身智能和机器人领域的代表企业,那宇树科技(Unitree)必须名列其榜。 最近,宇树科技的一项新变动消息在业界引发了不少关注和讨论,即: 宇树向其合作伙伴发布了一封公司名称变更函称,因…...
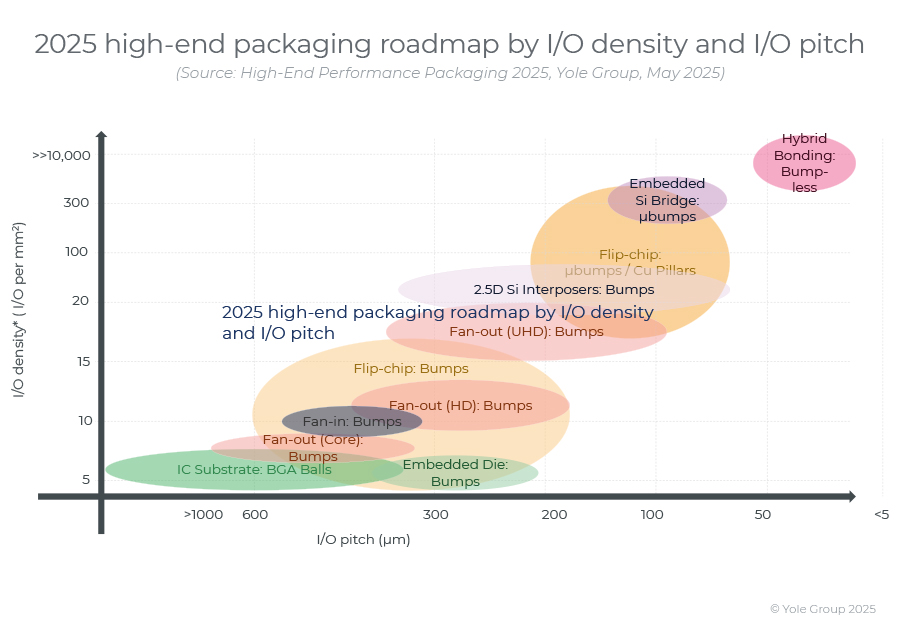
高端性能封装正在突破性能壁垒,其芯片集成技术助力人工智能革命。
2024 年,高端封装市场规模为 80 亿美元,预计到 2030 年将超过 280 亿美元,2024-2030 年复合年增长率为 23%。 细分到各个终端市场,最大的高端性能封装市场是“电信和基础设施”,2024 年该市场创造了超过 67% 的收入。…...
)
背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述 背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类: 01 背包:每件物品最多选 1 次(选或不选&#…...
