背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述
背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类:
- 01 背包:每件物品最多选 1 次(选或不选)。
- 完全背包:每件物品可选无限次。
本文将深入解析两者的核心逻辑、状态转移及优化技巧,并通过 Java 代码实现典型场景。
二、01 背包问题:选或不选的博弈
问题描述
给定背包容量 W 和 N 个物品(每个物品重量 w[i]、价值 v[i]),每个物品最多选 1 次,求背包能承载的最大价值。
核心思路
1. 状态定义
dp[j]:背包容量为j时能获得的最大价值。
2. 状态转移方程
dp[j] = max(dp[j], dp[j - w[i]] + v[i])
- 选第
i件物品:需确保容量j >= w[i],价值为前i-1件物品装入容量j-w[i]的背包价值 + 当前物品价值。 - 不选第
i件物品:价值与前i-1件物品装入容量j的背包价值相同。
3. 关键实现细节
- 倒序遍历容量:从
W到w[i]倒序枚举,避免重复选择同一物品。 - 空间优化:使用一维数组代替二维数组,降低空间复杂度至
O(W)。
示例分析
场景:背包容量 W=4,物品列表 [(w=2, v=3), (w=1, v=2), (w=3, v=4)]。
二维 DP 表演变:
| 容量 \ 物品 | 0(无) | 物品 1 (2,3) | 物品 2 (1,2) | 物品 3 (3,4) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 2 | 2 |
| 2 | 0 | 3 | 3 | 3 |
| 3 | 0 | 3 | 5 | 5 |
| 4 | 0 | 3 | 5 | 5 |
一维优化 Java 代码:
public class Knapsack01 {public static int solve(int[] w, int[] v, int W) {int N = w.length;int[] dp = new int[W + 1]; // dp[j]表示容量j的最大价值for (int i = 0; i < N; i++) { // 遍历每个物品for (int j = W; j >= w[i]; j--) { // 倒序遍历容量,避免重复选dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]);}}return dp[W];}public static void main(String[] args) {int[] w = {2, 1, 3};int[] v = {3, 2, 4};int W = 4;System.out.println("01背包最大价值:" + solve(w, v, W)); // 输出:5}
}
三、完全背包问题:无限选择的智慧
问题描述
与 01 背包不同,完全背包允许每件物品选无限次,求背包能承载的最大价值。
核心思路
1. 状态定义
同 01 背包,dp[j] 表示容量为 j 时的最大价值。
2. 状态转移方程
dp[j] = max(dp[j], dp[j - w[i]] + v[i])
- 允许重复选择:由于每件物品可选多次,需正序遍历容量(从
w[i]到W),确保当前物品可被多次选取。
3. 关键实现细节
- 正序遍历容量:从
w[i]到W正序枚举,允许同一件物品被多次计算。
示例分析
场景:背包容量 W=4,物品列表同 01 背包示例(允许无限选)。
二维 DP 表演变:
| 容量 \ 物品 | 0(无) | 物品 1 (2,3) | 物品 2 (1,2) | 物品 3 (3,4) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 2 | 2 |
| 2 | 0 | 3 | 4 | 4 |
| 3 | 0 | 3 | 6 | 6 |
| 4 | 0 | 6 | 8 | 8 |
一维优化 Java 代码:
public class KnapsackComplete {public static int solve(int[] w, int[] v, int W) {int N = w.length;int[] dp = new int[W + 1];for (int i = 0; i < N; i++) { // 遍历每个物品for (int j = w[i]; j <= W; j++) { // 正序遍历容量,允许重复选dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]);}}return dp[W];}public static void main(String[] args) {int[] w = {2, 1, 3};int[] v = {3, 2, 4};int W = 4;System.out.println("完全背包最大价值:" + solve(w, v, W)); // 输出:8(选4件物品2)}
}
四、核心对比:01 背包 vs 完全背包
| 特性 | 01 背包 | 完全背包 |
|---|---|---|
| 物品选择 | 每个物品最多选 1 次 | 每个物品可选无限次 |
| 容量遍历顺序 | 倒序(从 W 到 w [i]) | 正序(从 w [i] 到 W) |
| 状态更新逻辑 | 基于 “旧状态” 避免重复 | 基于 “新状态” 允许重复 |
| 时间复杂度 | O(N×W) | O(N×W) |
| 典型场景 | 物品限购、资源分配 | 货币兑换、原料无限供应 |
五、实战应用:LeetCode 经典题目
1. 01 背包应用:分割等和子集(LeetCode 416)
问题描述:判断数组是否可分割成两个和相等的子集。
思路:转化为 01 背包问题,目标容量为 total/2,判断是否能恰好装满。
public class CanPartition {public static boolean canPartition(int[] nums) {int total = sum(nums);if (total % 2 != 0) return false;int target = total / 2;boolean[] dp = new boolean[target + 1];dp[0] = true; // 容量0时有一种方案(不选任何物品)for (int num : nums) {for (int j = target; j >= num; j--) { // 倒序遍历防重复dp[j] = dp[j] || dp[j - num];}}return dp[target];}private static int sum(int[] nums) {return Arrays.stream(nums).sum();}public static void main(String[] args) {int[] nums = {1, 5, 11, 5};System.out.println(canPartition(nums)); // 输出:true(子集和为11)}
}
2. 完全背包应用:零钱兑换(LeetCode 322)
问题描述:用最少硬币数组成金额 amount,硬币可重复使用。
思路:转化为完全背包问题,目标是最小化物品数量(硬币数)。
public class CoinChange {public static int coinChange(int[] coins, int amount) {int[] dp = new int[amount + 1];Arrays.fill(dp, Integer.MAX_VALUE);dp[0] = 0; // 金额0时需0枚硬币for (int coin : coins) {for (int j = coin; j <= amount; j++) { // 正序遍历允许多选if (dp[j - coin] != Integer.MAX_VALUE) {dp[j] = Math.min(dp[j], dp[j - coin] + 1);}}}return dp[amount] == Integer.MAX_VALUE ? -1 : dp[amount];}public static void main(String[] args) {int[] coins = {1, 2, 5};int amount = 11;System.out.println(coinChange(coins, amount)); // 输出:3(5+5+1)}
}
六、优化技巧与变种问题
1. 空间优化
- 一维数组代替二维数组,空间复杂度从
O(N×W)降至O(W)。
2. 多重背包转化
若物品有数量限制(如最多选 k 件),可通过二进制拆分转化为 01 背包问题。例如,最多选 3 件可拆分为 1 件、2 件两个物品。
3. 常见变种
- 恰好装满背包的方案数:初始化
dp[0] = 1,其余为 0,通过加法原理计算方案数。 - 二维费用背包:增加一维状态(如重量和体积),状态转移为
dp[j][k] = max(...)。
七、总结与学习建议
核心口诀
- 01 背包:倒序遍历防重复,选或不选取最值。
- 完全背包:正序遍历允重复,同物多次算价值。
练习推荐
- 01 背包:LeetCode 494. 目标和
- 完全背包:LeetCode 518. 零钱兑换 II(求方案数,需正序遍历 + 组合逻辑)
通过对比学习 01 背包与完全背包的核心逻辑,掌握动态规划的状态转移思想,可有效应对背包问题的各类变种。建议结合具体题目反复练习,加深对 “状态定义” 和 “遍历顺序” 的理解。
相关文章:
)
背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述 背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类: 01 背包:每件物品最多选 1 次(选或不选&#…...

Python第七周作业
Python第七周作业 文章目录 Python第七周作业 1.使用open以只读模式打开文件data.txt,并逐行打印内容 2.使用pathlib模块获取当前脚本的绝对路径,并创建logs目录(若不存在) 3.递归遍历目录data,输出所有.csv文件的路径…...

Qt的学习(二)
1. 创建Hello Word 两种方式,实现helloworld: 1.通过图形化的方式,在界面上创建出一个控件,显示helloworld 2.通过纯代码的方式,通过编写代码,在界面上创建控件, 显示hello world; …...

算法刷题-回溯
今天给大家分享的还是一道关于dfs回溯的问题,对于这类问题大家还是要多刷和总结,总体难度还是偏大。 对于回溯问题有几个关键点: 1.首先对于这类回溯可以节点可以随机选择的问题,要做mian函数中循环调用dfs(i&#x…...
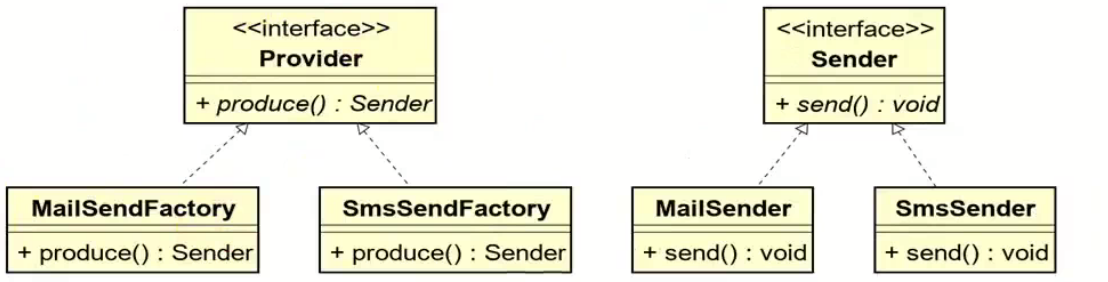
工厂方法模式和抽象工厂方法模式的battle
1.案例直接上手 在这个案例里面,我们会实现这个普通的工厂方法,并且对比这个普通工厂方法和我们直接创建对象的差别在哪里,为什么需要一个工厂: 下面的这个是我们的这个案例里面涉及到的接口和对应的实现类: 两个发…...

深入解析 ReentrantLock:原理、公平锁与非公平锁的较量
ReentrantLock 是 Java 中 java.util.concurrent.locks 包下的一个重要类,用于实现线程同步,支持可重入性,并且可以选择公平锁或非公平锁的实现方式。下面将详细介绍 ReentrantLock 的实现原理以及公平锁和非公平锁的区别。 ReentrantLock 实现原理 基本架构 ReentrantLo…...

鸿蒙Navigation路由导航-基本使用介绍
1. Navigation介绍 Navigation组件是路由导航的根视图容器,一般作为Page页面的根容器使用,其内部默认包含了标题栏、内容区和工具栏,其中内容区默认首页显示导航内容(Navigation的子组件)或非首页显示(Nav…...

JavaScript 标签加载
目录 JavaScript 标签加载script 标签的 async 和 defer 属性,分别代表什么,有什么区别1. 普通 script 标签2. async 属性3. defer 属性4. type"module"5. 各种加载方式的对比6. 使用建议 JavaScript 标签加载 script 标签的 async 和 defer …...

「Java基本语法」变量的使用
变量定义 变量是程序中存储数据的容器,用于保存可变的数据值。在Java中,变量必须先声明后使用,声明时需指定变量的数据类型和变量名。 语法 数据类型 变量名 [ 初始值]; 示例:声明与初始化 public class VariableDemo {publi…...

CMS内容管理系统的设计与实现:多站点模式的实现
在一套内容管理系统中,其实有很多站点,比如企业门户网站,产品手册,知识帮助手册等,因此会需要多个站点,甚至PC、mobile、ipad各有一个站点。 每个站点关联的有站点所在目录及所属的域名。 一、站点表设计…...

用鸿蒙HarmonyOS5实现国际象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的国际象棋小游戏的完整实现代码,使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├── …...
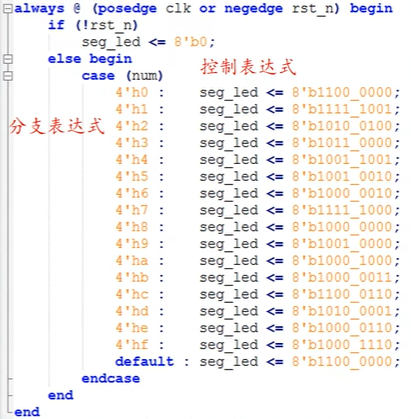
ZYNQ学习记录FPGA(二)Verilog语言
一、Verilog简介 1.1 HDL(Hardware Description language) 在解释HDL之前,先来了解一下数字系统设计的流程:逻辑设计 -> 电路实现 -> 系统验证。 逻辑设计又称前端,在这个过程中就需要用到HDL,正文…...

k8s从入门到放弃之Pod的容器探针检测
k8s从入门到放弃之Pod的容器探针检测 在Kubernetes(简称K8s)中,容器探测是指kubelet对容器执行定期诊断的过程,以确保容器中的应用程序处于预期的状态。这些探测是保障应用健康和高可用性的重要机制。Kubernetes提供了两种种类型…...
:电商转化率优化与网站性能的底层逻辑)
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑
精益数据分析(98/126):电商转化率优化与网站性能的底层逻辑 在电子商务领域,转化率与网站性能是决定商业成败的核心指标。今天,我们将深入解析不同类型电商平台的转化率基准,探讨页面加载速度对用户行为的…...

Java中HashMap底层原理深度解析:从数据结构到红黑树优化
一、HashMap概述与核心特性 HashMap作为Java集合框架中最常用的数据结构之一,是基于哈希表的Map接口非同步实现。它允许使用null键和null值(但只能有一个null键),并且不保证映射顺序的恒久不变。与Hashtable相比,Hash…...
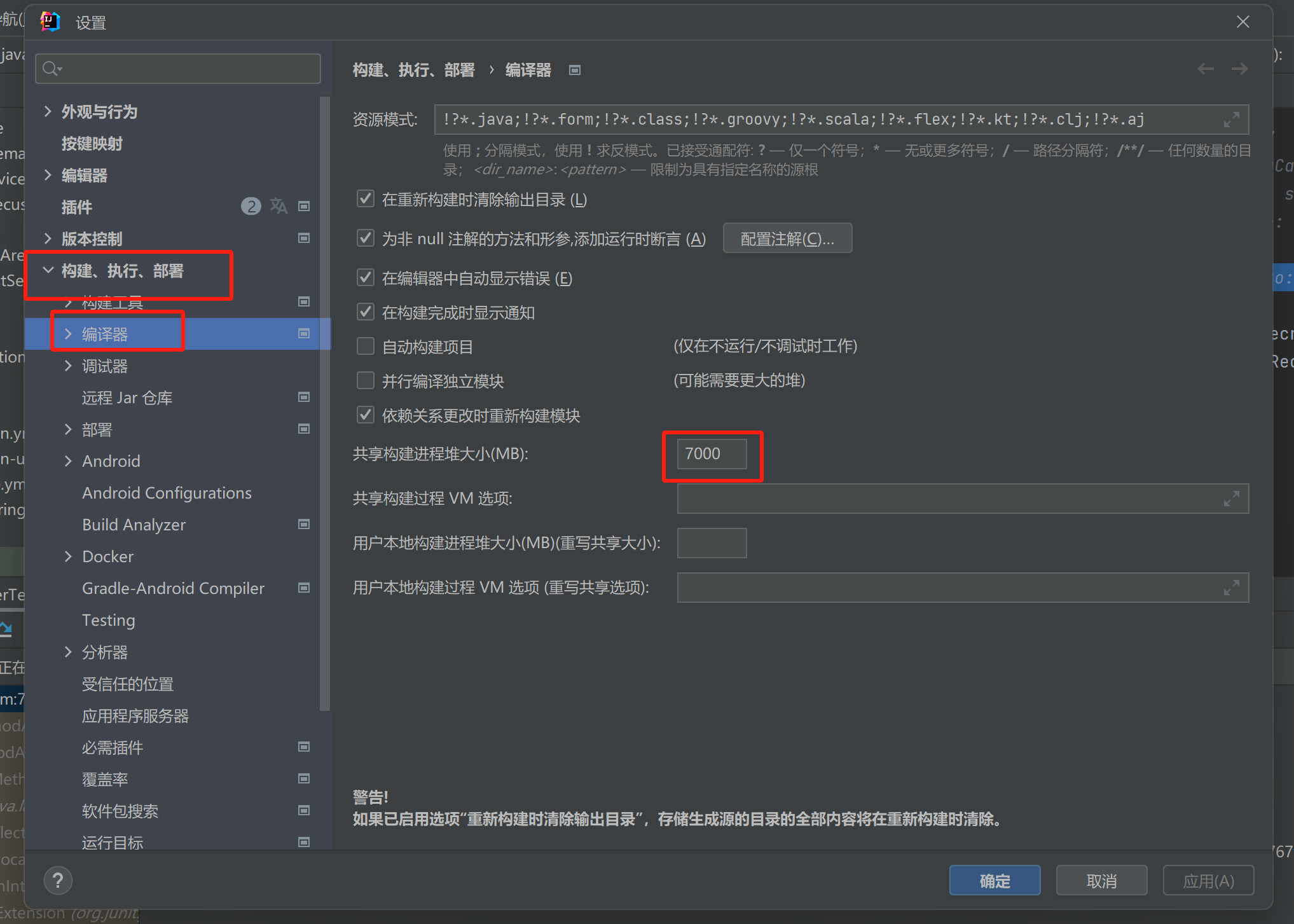
【记录坑点问题】IDEA运行:maven-resources-production:XX: OOM: Java heap space
问题:IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案:将编译的堆内存增加一点 位置:设置setting-》构建菜单build-》编译器Complier...

【阅读笔记】MemOS: 大语言模型内存增强生成操作系统
核心速览 研究背景 研究问题:这篇文章要解决的问题是当前大型语言模型(LLMs)在处理内存方面的局限性。LLMs虽然在语言感知和生成方面表现出色,但缺乏统一的、结构化的内存架构。现有的方法如检索增强生成(RA…...

Java中栈的多种实现类详解
Java中栈的多种实现类详解:Stack、LinkedList与ArrayDeque全方位对比 前言一、Stack类——Java最早的栈实现1.1 Stack类简介1.2 常用方法1.3 优缺点分析 二、LinkedList类——灵活的双端链表2.1 LinkedList类简介2.2 常用方法2.3 优缺点分析 三、ArrayDeque类——高…...

6.计算机网络核心知识点精要手册
计算机网络核心知识点精要手册 1.协议基础篇 网络协议三要素 语法:数据与控制信息的结构或格式,如同语言中的语法规则语义:控制信息的具体含义和响应方式,规定通信双方"说什么"同步:事件执行的顺序与时序…...

基于Uniapp的HarmonyOS 5.0体育应用开发攻略
一、技术架构设计 1.混合开发框架选型 (1)使用Uniapp 3.8版本支持ArkTS编译 (2)通过uni-harmony插件调用原生能力 (3)分层架构设计: graph TDA[UI层] -->|Vue语法| B(Uniapp框架)B --&g…...

【笔记】AI Agent 项目 SUNA 部署 之 Docker 构建记录
#工作记录 构建过程记录 Microsoft Windows [Version 10.0.27871.1000] (c) Microsoft Corporation. All rights reserved.(suna-py3.12) F:\PythonProjects\suna>python setup.py --admin███████╗██╗ ██╗███╗ ██╗ █████╗ ██╔════╝…...

五、jmeter脚本参数化
目录 1、脚本参数化 1.1 用户定义的变量 1.1.1 添加及引用方式 1.1.2 测试得出用户定义变量的特点 1.2 用户参数 1.2.1 概念 1.2.2 位置不同效果不同 1.2.3、用户参数的勾选框 - 每次迭代更新一次 总结用户定义的变量、用户参数 1.3 csv数据文件参数化 1、脚本参数化 …...

python基础语法Ⅰ
python基础语法Ⅰ 常量和表达式变量是什么变量的语法1.定义变量使用变量 变量的类型1.整数2.浮点数(小数)3.字符串4.布尔5.其他 动态类型特征注释注释是什么注释的语法1.行注释2.文档字符串 注释的规范 常量和表达式 我们可以把python当作一个计算器,来进行一些算术…...
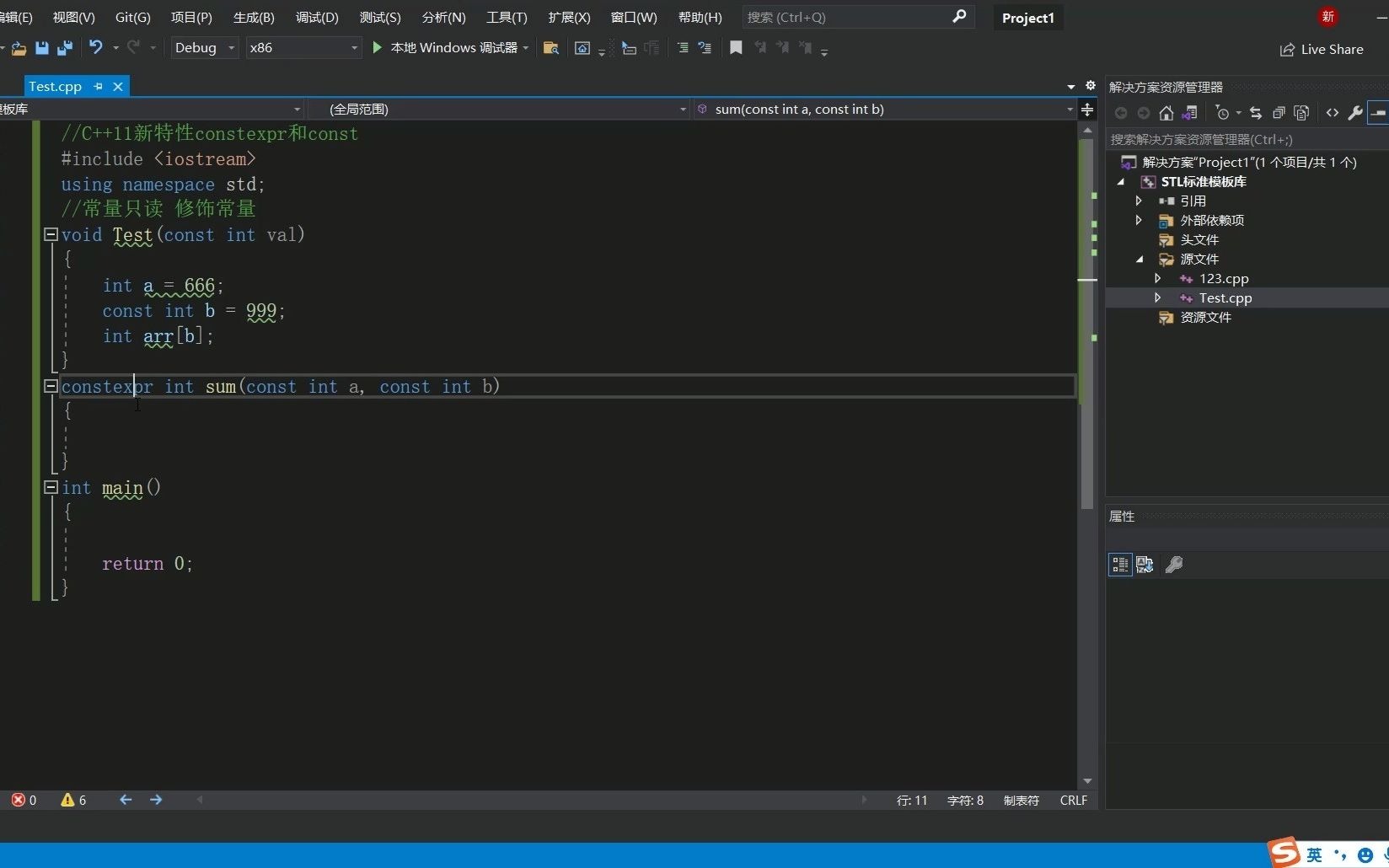
C++11 constexpr和字面类型:从入门到精通
文章目录 引言一、constexpr的基本概念与使用1.1 constexpr的定义与作用1.2 constexpr变量1.3 constexpr函数1.4 constexpr在类构造函数中的应用1.5 constexpr的优势 二、字面类型的基本概念与使用2.1 字面类型的定义与作用2.2 字面类型的应用场景2.2.1 常量定义2.2.2 模板参数…...

EEG-fNIRS联合成像在跨频率耦合研究中的创新应用
摘要 神经影像技术对医学科学产生了深远的影响,推动了许多神经系统疾病研究的进展并改善了其诊断方法。在此背景下,基于神经血管耦合现象的多模态神经影像方法,通过融合各自优势来提供有关大脑皮层神经活动的互补信息。在这里,本研…...

python打卡day49@浙大疏锦行
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 一、通道注意力模块复习 & CBAM实现 import torch import torch.nn as nnclass CBAM(nn.Module):def __init__…...

Qt Quick Controls模块功能及架构
Qt Quick Controls是Qt Quick的一个附加模块,提供了一套用于构建完整用户界面的UI控件。在Qt 6.0中,这个模块经历了重大重构和改进。 一、主要功能和特点 1. 架构重构 完全重写了底层架构,与Qt Quick更紧密集成 移除了对Qt Widgets的依赖&…...

手动给中文分词和 直接用神经网络RNN做有什么区别
手动分词和基于神经网络(如 RNN)的自动分词在原理、实现方式和效果上有显著差异,以下是核心对比: 1. 实现原理对比 对比维度手动分词(规则 / 词典驱动)神经网络 RNN 分词(数据驱动)…...
C++中vector类型的介绍和使用
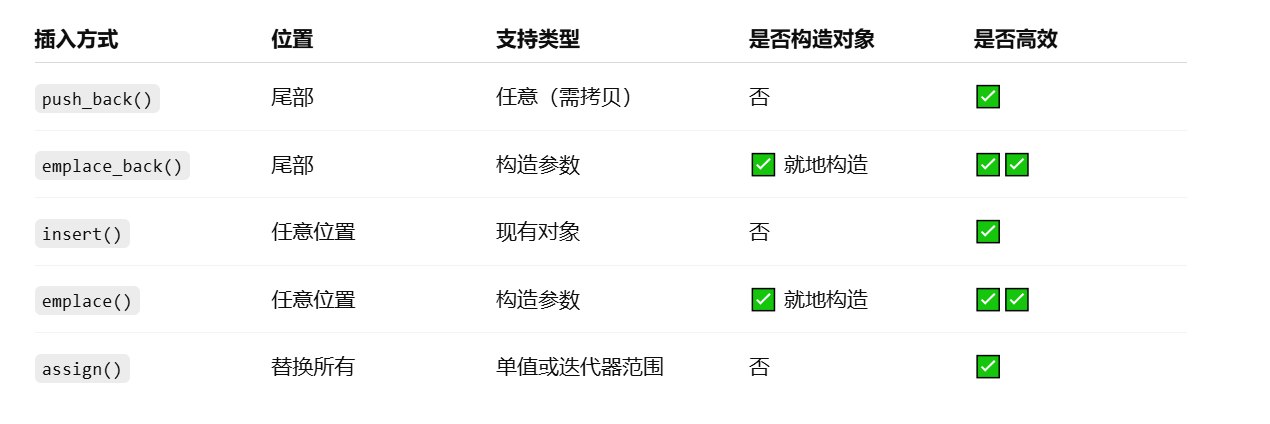
文章目录 一、vector 类型的简介1.1 基本介绍1.2 常见用法示例1.3 常见成员函数简表 二、vector 数据的插入2.1 push_back() —— 在尾部插入一个元素2.2 emplace_back() —— 在尾部“就地”构造对象2.3 insert() —— 在任意位置插入一个或多个元素2.4 emplace() —— 在任意…...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...
