LeetCode130. Surrounded Regions
文章目录
- 一、题目
- 二、题解
一、题目
Given an m x n matrix board containing ‘X’ and ‘O’, capture all regions that are 4-directionally surrounded by ‘X’.
A region is captured by flipping all 'O’s into 'X’s in that surrounded region.
Example 1:
Input: board = [[“X”,“X”,“X”,“X”],[“X”,“O”,“O”,“X”],[“X”,“X”,“O”,“X”],[“X”,“O”,“X”,“X”]]
Output: [[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“X”,“X”,“X”],[“X”,“O”,“X”,“X”]]
Explanation: Notice that an ‘O’ should not be flipped if:
- It is on the border, or
- It is adjacent to an ‘O’ that should not be flipped.
The bottom ‘O’ is on the border, so it is not flipped.
The other three ‘O’ form a surrounded region, so they are flipped.
Example 2:
Input: board = [[“X”]]
Output: [[“X”]]
Constraints:
m == board.length
n == board[i].length
1 <= m, n <= 200
board[i][j] is ‘X’ or ‘O’.
二、题解
visited数组法——使用额外空间
与上题的方法类似,遍历四条边上值为’O’的值,并找出与其相邻的所有’O’,将其标记为已走过,最后遍历整张图,找到没走过的值为’O’的各自,并将其修改为’X’即可。本方法由于使用了visited数组,因此空间复杂度较高。
class Solution {
public:int dirs[4][2] = {1,0,0,1,-1,0,0,-1};void dfs(vector<vector<char>>& board,vector<vector<bool>>& visted,int x,int y){visted[x][y] = true;for(int i = 0;i < 4;i++){int nextX = x + dirs[i][0];int nextY = y + dirs[i][1];if(nextX < 0 || nextX >= board.size() || nextY < 0 || nextY >= board[0].size()) continue;if(board[nextX][nextY] == 'O' && visted[nextX][nextY] == false){visted[nextX][nextY] = true;dfs(board,visted,nextX,nextY);}}}void solve(vector<vector<char>>& board) {int m = board.size();int n = board[0].size();vector<vector<bool>> visted(m,vector<bool>(n,false));//对左和右进行遍历for(int i = 0;i < m;i++){if(board[i][0] == 'O' && visted[i][0] == false) dfs(board,visted,i,0);if(board[i][n-1] == 'O' && visted[i][n-1] == false) dfs(board,visted,i,n-1);}//对上和下进行遍历for(int j = 1;j < n - 1;j++){if(board[0][j] == 'O' && visted[0][j] == false) dfs(board,visted,0,j);if(board[m-1][j] == 'O' && visted[m-1][j] == false) dfs(board,visted,m-1,j);}//改变被包围飞地的值for(int i = 0;i < m;i++){for(int j = 0;j < n;j++){if(board[i][j] == 'O' && visted[i][j] == false) board[i][j] = 'X';}}}
};
不使用额外空间的方法——直接在原数组中使用数字A进行标记
class Solution {
public:int dirs[4][2] = {1,0,0,1,-1,0,0,-1};void dfs(vector<vector<char>>& board,int x,int y){board[x][y] = 'A';for(int i = 0;i < 4;i++){int nextX = x + dirs[i][0];int nextY = y + dirs[i][1];if(nextX < 0 || nextX >= board.size() || nextY < 0 || nextY >= board[0].size()) continue;if(board[nextX][nextY] == 'O'){board[nextX][nextY] = 'A';dfs(board,nextX,nextY);}}}void solve(vector<vector<char>>& board) {int m = board.size();int n = board[0].size();//对左和右进行遍历for(int i = 0;i < m;i++){if(board[i][0] == 'O') dfs(board,i,0);if(board[i][n-1] == 'O') dfs(board,i,n-1);}//对上和下进行遍历for(int j = 1;j < n - 1;j++){if(board[0][j] == 'O') dfs(board,0,j);if(board[m-1][j] == 'O') dfs(board,m-1,j);}//改变被包围飞地的值for(int i = 0;i < m;i++){for(int j = 0;j < n;j++){if(board[i][j] == 'O') board[i][j] = 'X';else if(board[i][j] == 'A') board[i][j] = 'O';}}}
};
相关文章:

LeetCode130. Surrounded Regions
文章目录 一、题目二、题解 一、题目 Given an m x n matrix board containing ‘X’ and ‘O’, capture all regions that are 4-directionally surrounded by ‘X’. A region is captured by flipping all O’s into X’s in that surrounded region. Example 1: Input…...

【实战教程】PHP如何轻松对接腾讯云COS,实现文件上传下载?
腾讯云提供了一系列丰富的云服务,其中包括对象存储(Cloud Object Storage,简称COS),它是一种高可靠性、可扩展性强的云存储服务。本文将介绍如何使用PHP对接腾讯云COS存储服务,实现文件的上传和下载功能。 …...

pytorch学习10-网络模型的保存和加载
系列文章目录 pytorch学习1-数据加载以及Tensorboard可视化工具pytorch学习2-Transforms主要方法使用pytorch学习3-torchvisin和Dataloader的使用pytorch学习4-简易卷积实现pytorch学习5-最大池化层的使用pytorch学习6-非线性变换(ReLU和sigmoid)pytorc…...

SQL Server 2016(分离和附加数据库)
1、实验环境。 基于上一个实验《SQL Server(创建数据库)》 2、需求描述。 class数据库的数据文件和事务日志文件都位于C:\db_class目录下。现在需要把class数据库的数据文件和事务日志文件分开存放,数据文件class.mdf存放于原位置࿰…...
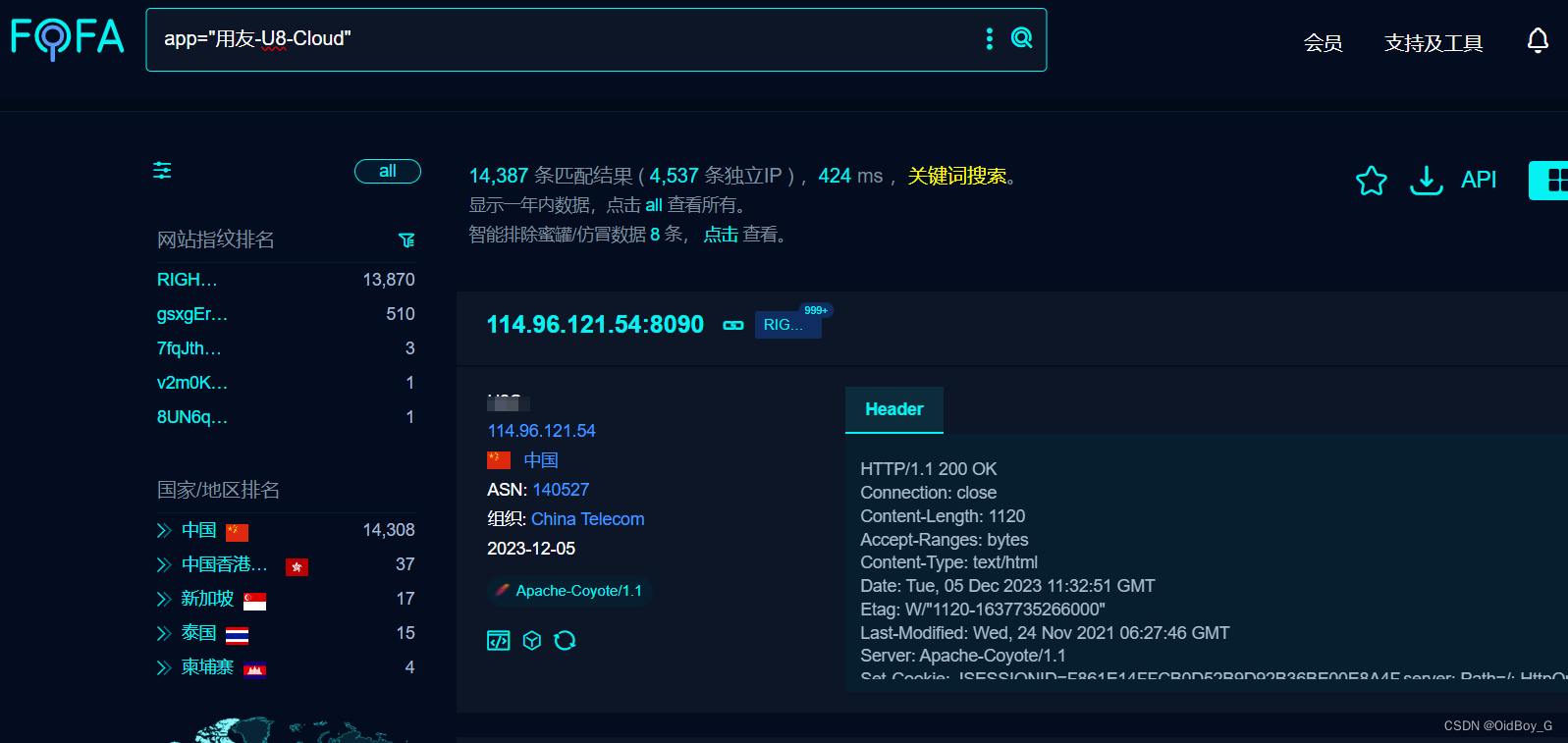
用友U8 Cloud RegisterServlet SQL注入漏洞复现
0x01 产品简介 用友U8 Cloud是用友推出的新一代云ERP,主要聚焦成长型、创新型企业,提供企业级云ERP整体解决方案。 0x02 漏洞概述 用友U8 Cloud RegisterServlet接口处存在SQL注入漏洞,未授权的攻击者可通过此漏洞获取数据库权限,从而盗取用户数据,造成用户信息泄露。 …...
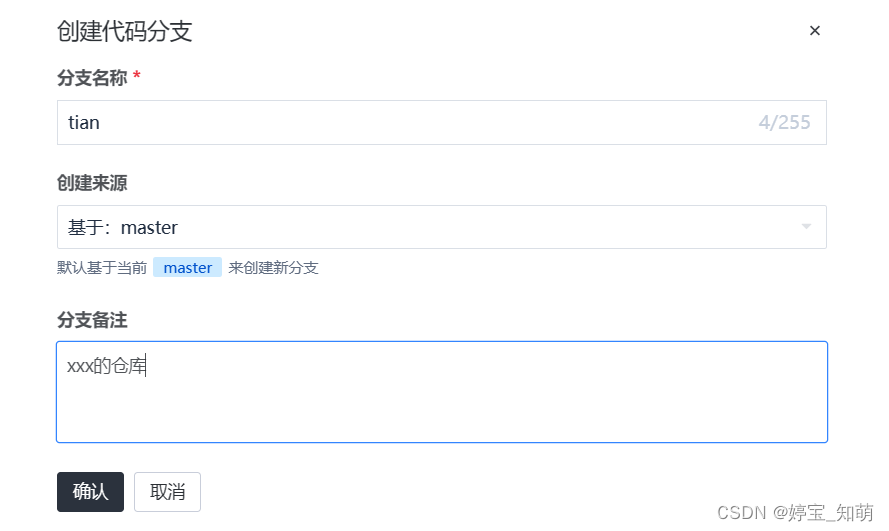
coding创建远程分支。并拉取远程新分支+推送代码
进入coding ----项目----代码仓库---点击 下拉之后查看全部----创建分支 创建分支之后执行下面命令 git branch -a // 查看所有分支 这个时候发现自己创建的分支没有显示这是因为自己在远程创建了分支但是本地还没有分支 执行 git fetch命令 用于从远程仓库获取最新的提交…...

坚鹏:中国工商银行内蒙古分行数字化转型发展现状与成功案例培训
中国工商银行围绕“数字生态、数字资产、数字技术、数字基建、数字基因”五维布局,深入推进数字化转型,加快形成体系化、生态化实施路径,促进科技与业务加速融合,以“数字工行”建设推动“GBC”(政务、企业、个人&…...
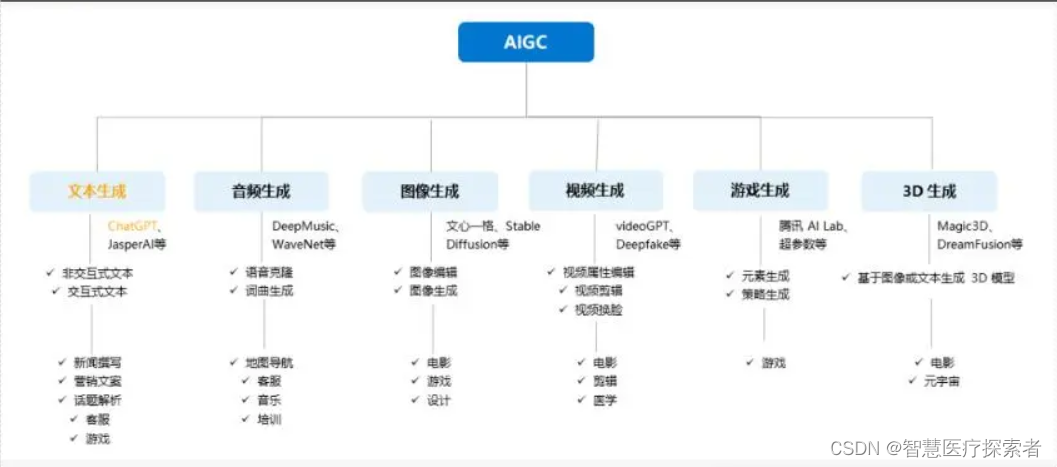
AIGC发展史
1 AIGC概况 1.1 AIGC定义 AIGC(AI Generated Content)是指利用人工智能技术生成的内容。它也被认为是继PGC,UGC之后的新型内容生产方式,AI绘画、AI写作等都属于AIGC的具体形式。2022年AIGC发展速度惊人,迭代速度更是呈现指数级发…...
)
面试题库之JAVA基础篇(二)
String 只读字符串。每次操作会隐式的在内存中new一个跟原字符串一样的StringBuilder对象,然后append号后面的字符串。 StringBuilder 可变字符串对象。线程不安全。 StringBuffer 可变字符串对象。线程安全。 数组 一种线性数据结构,使用连续的…...

[Rust] 可迭代类型, 迭代器, 如何正确的创建自定义可迭代类型
在 Rust 中, for 语句的执行依赖于类型对于 IntoIterator 的实现, 如果某类型实现了这个 trait, 那么它就可以直接使用 for 进行循环. 直接实现 在 Rust 中, 如果一个类型实现了 Iterator, 那么它会被同时实现 IntoIterator, 具体逻辑是返回自身, 因为自身就是迭代器. 但是如…...

MySQL中,text,mediumtext, 和 longtext字符类型
需求 由于项目需要,需要在mysql数据库,储存长文本,长文本格式可能为markdown也可能为html。 思路 测试存入html时,字符类型为varcar 255。很明显字符长度达不到要求。数据库抛错,修改字符类型 解决方案 将原本的字…...
网页开发 JS基础
目录 JS概述 基本语法 数据类型内置方法 DOM对象 查找标签 绑定事件 操作标签 jQuery 查找标签 绑定事件 操作标签 Ajax请求 数据接口 前后端分离 ajax的使用 JS概述 一门弱类型的编程语言,属于基于对象和基于原型的脚本语言. 1 直接编写<script>console…...
如何在财税行业查找批量客户?
现在市场上代记账公司也不算少,做过这行的都知道,最初呢行业竞争不强,都是靠地推、老客户转介绍,或者长期以往的蹲守各个地区的工商注册服务中心,找那些才注册企业的老板或者创业者。但是,随着市场经济的发…...

IntelliJ IDEA详细完整安装教程
IntelliJ IDEA 是一款强大的Java集成开发环境,以下是安装和使用教程: 1. 下载IntelliJ IDEA:访问JetBrains官网(jetbrains.com),点击“Download”按钮,选择适合自己操作系统的版本进行下载。 2.…...
)
【.NET Core】Linq查询运算符(一)
【.NET Core】Linq查询运算符(一) 文章目录 【.NET Core】Linq查询运算符(一)一、概述二、筛选数据三、投影运算3.1 Select 3.2 SelectMany3.3 Zip3.4 Select 与 SelectMany 四、Set(设置)运算4.1 Distinct…...

Python sorted函数及用法以及如何用json模块存储数据
Python sorted函数及用法 sorted() 函数与 reversed() 函数类似,该函数接收一个可迭代对象作为参数,返回一个对元素排序的列表。 在交互式解释器中测试该函数,可以看到如下运行过程: >>> a [20, 30, -1.2, 3.5, 90, 3.…...
使用opencv将sRGB格式的图片转换为BT.2020格式【sRGB】【BT.2020】
将sRGB格式的图片转换为BT.2020格式涉及到两个步骤:首先将sRGB转换到线性RGB,然后将线性RGB转换到BT.2020。这是因为sRGB图像通常使用伽马校正,而BT.2020工作在线性色彩空间中。 从sRGB到线性RGB:sRGB图像首先需要进行伽马校正解码…...

聊天注意事项
聊天成功的核心就是双方都能舒服 有些人不会聊天是缺乏引导性 聊天聊两句话就没了 聊天要把话题引导向对方 从倾诉者变为倾听者 才能不断交流 沟通不是一个人的独角戏 每个人都渴望被理解 要注意倾听别人说的话 不要只顾自己说一大堆,别人都瞌睡了 不要查户口式问…...
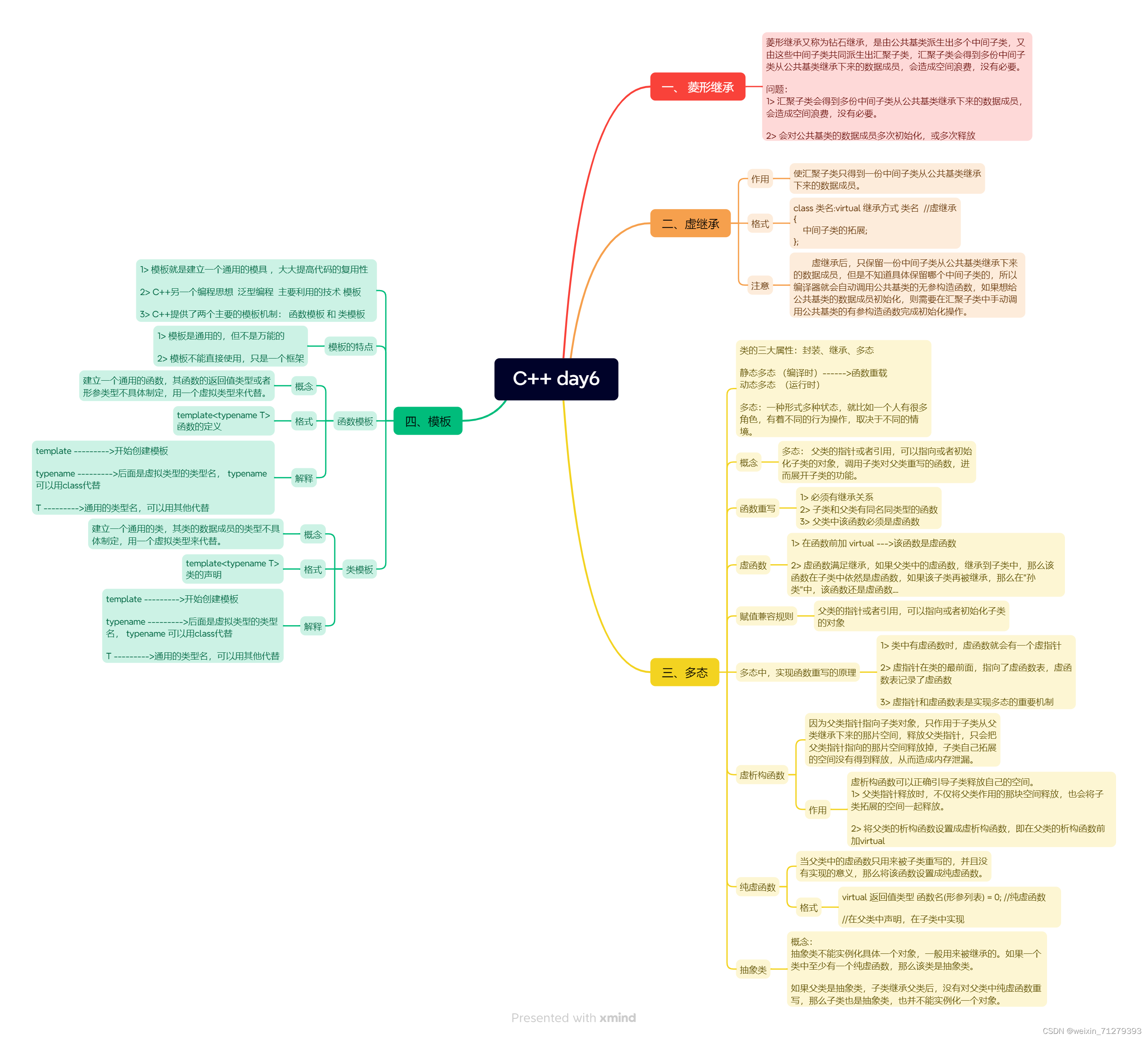
12.5 作业
1, 以下是一个简单的比喻,将多态概念与生活中的实际情况相联系: 比喻:动物园的讲解员和动物表演 想象一下你去了一家动物园,看到了许多不同种类的动物,如狮子、大象、猴子等。现在,动物园里有…...

深入理解指针3
hello,各位小伙伴,本篇文章跟大家一起继续深入学习指针,感谢大家对我上一篇的支持,如有什么问题,还请多多指教 如果本篇文章对你有帮助,还请各位点点赞!!! 话不多说&am…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...
