【深度学习笔记】09 权重衰减
09 权重衰减
- 范数和权重衰减
- 利用高维线性回归实现权重衰减
- 初始化模型参数
- 定义 L 2 L_2 L2范数惩罚
- 定义训练代码实现
- 忽略正则化直接训练
- 使用权重衰减
- 权重衰减的简洁实现
范数和权重衰减
在训练参数化机器学习模型时,权重衰减(decay weight)是最广泛应用的正则化技术之一,它通常也被称为 L 2 L_2 L2正则化。这项技术通过函数与零的距离来衡量函数的复杂度,
因为在所有函数 f f f中,函数 f = 0 f = 0 f=0(所有输入都得到值 0 0 0)
在某种意义上是最简单的。
一种简单的方法是通过线性函数
f ( x ) = w ⊤ x f(\mathbf{x}) = \mathbf{w}^\top \mathbf{x} f(x)=w⊤x
中的权重向量的某个范数来度量其复杂性,
例如 ∥ w ∥ 2 \| \mathbf{w} \|^2 ∥w∥2。
要保证权重向量比较小,
最常用方法是将其范数作为惩罚项加到最小化损失的问题中。
将原来的训练目标最小化训练标签上的预测损失,
调整为最小化预测损失和惩罚项之和。
损失由下式给出:
L ( w , b ) = 1 n ∑ i = 1 n 1 2 ( w ⊤ x ( i ) + b − y ( i ) ) 2 . L(\mathbf{w}, b) = \frac{1}{n}\sum_{i=1}^n \frac{1}{2}\left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right)^2. L(w,b)=n1i=1∑n21(w⊤x(i)+b−y(i))2.
x ( i ) \mathbf{x}^{(i)} x(i)是样本 i i i的特征,
y ( i ) y^{(i)} y(i)是样本 i i i的标签,
( w , b ) (\mathbf{w}, b) (w,b)是权重和偏置参数。
为了惩罚权重向量的大小,
必须以某种方式在损失函数中添加 ∥ w ∥ 2 \| \mathbf{w} \|^2 ∥w∥2,
我们通过正则化常数 λ \lambda λ来描述这种权衡,
这是一个非负超参数,我们使用验证数据拟合:
L ( w , b ) + λ 2 ∥ w ∥ 2 , L(\mathbf{w}, b) + \frac{\lambda}{2} \|\mathbf{w}\|^2, L(w,b)+2λ∥w∥2,
对于 λ = 0 \lambda = 0 λ=0,我们恢复了原来的损失函数。
对于 λ > 0 \lambda > 0 λ>0,我们限制 ∥ w ∥ \| \mathbf{w} \| ∥w∥的大小。
这里我们仍然除以 2 2 2:当我们取一个二次函数的导数时,
2 2 2和 1 / 2 1/2 1/2会抵消。
通过平方 L 2 L_2 L2范数,我们去掉平方根,留下权重向量每个分量的平方和。
这使得惩罚的导数很容易计算:导数的和等于和的导数。
L 2 L_2 L2正则化回归的小批量随机梯度下降更新如下式:
w ← ( 1 − η λ ) w − η ∣ B ∣ ∑ i ∈ B x ( i ) ( w ⊤ x ( i ) + b − y ( i ) ) . \begin{aligned} \mathbf{w} & \leftarrow \left(1- \eta\lambda \right) \mathbf{w} - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \mathbf{x}^{(i)} \left(\mathbf{w}^\top \mathbf{x}^{(i)} + b - y^{(i)}\right). \end{aligned} w←(1−ηλ)w−∣B∣ηi∈B∑x(i)(w⊤x(i)+b−y(i)).
我们根据估计值与观测值之间的差异来更新 w \mathbf{w} w。
然而,我们同时也在试图将 w \mathbf{w} w的大小缩小到零。
这就是为什么这种方法有时被称为权重衰减。
我们仅考虑惩罚项,优化算法在训练的每一步衰减权重。
与特征选择相比,权重衰减为我们提供了一种连续的机制来调整函数的复杂度。
较小的 λ \lambda λ值对应较少约束的 w \mathbf{w} w,
而较大的 λ \lambda λ值对 w \mathbf{w} w的约束更大。
是否对相应的偏置 b 2 b^2 b2进行惩罚在不同的实践中会有所不同,
在神经网络的不同层中也会有所不同。
通常,网络输出层的偏置项不会被正则化。
利用高维线性回归实现权重衰减
%matplotlib inline
import torch
from torch import nn
from d2l import torch as d2l
首先生成数据,生成公式如下:
y = 0.05 + ∑ i = 1 d 0.01 x i + ϵ where ϵ ∼ N ( 0 , 0.0 1 2 ) . y = 0.05 + \sum_{i = 1}^d 0.01 x_i + \epsilon \text{ where } \epsilon \sim \mathcal{N}(0, 0.01^2). y=0.05+i=1∑d0.01xi+ϵ where ϵ∼N(0,0.012).
选择标签是关于输入的线性函数。
标签同时被均值为0,标准差为0.01高斯噪声破坏。
为了使过拟合的效果更加明显,我们可以将问题的维数增加到 d = 200 d = 200 d=200,
并使用一个只包含20个样本的小训练集。
n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
train_data = d2l.synthetic_data(true_w, true_b, n_train)
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)
初始化模型参数
定义一个函数来随机初始化模型参数
def init_params():w = torch.normal(0, 1, size = (num_inputs, 1), requires_grad = True)b = torch.zeros(1, requires_grad = True)return [w, b]
定义 L 2 L_2 L2范数惩罚
def l2_penalty(w):return torch.sum(w.pow(2)) / 2
定义训练代码实现
下面的代码将模型拟合训练数据集,并在测试数据集上进行评估。
def train(lambd):w, b = init_params()net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_lossnum_epochs, lr = 100, 0.003animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',xlim=[5, num_epochs], legend=['train', 'test'])for epoch in range(num_epochs):for X, y in train_iter:# 增加了L2范数惩罚项,# 广播机制使l2_penalty(w)成为一个长度为batch_size的向量l = loss(net(X), y) + lambd * l2_penalty(w)l.sum().backward()d2l.sgd([w, b], lr, batch_size)if (epoch + 1) % 5 == 0:animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),d2l.evaluate_loss(net, test_iter, loss)))print('w的L2范数是:', torch.norm(w).item())
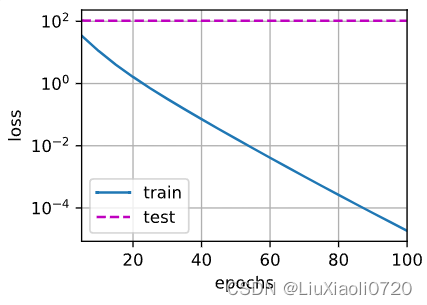
忽略正则化直接训练
用lamdb=0禁用权重衰减后运行代码。此时训练误差有所减少,但测试误差没有减少,这意味着出现了严重的过拟合。
train(lambd = 0)
w的L2范数是: 14.971677780151367
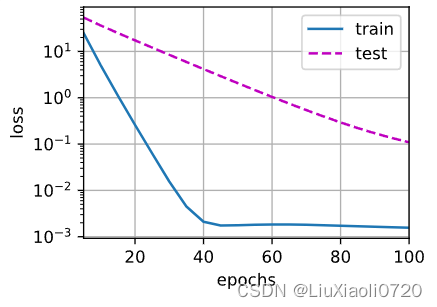
使用权重衰减
使用权重衰减来运行代码。此时训练误差增大,但测试误差减小。这正是我们期望从正则化中得到的效果。
train(lambd = 3)
w的L2范数是: 0.34405317902565
权重衰减的简洁实现
在实例化优化器时直接通过weight_decay指定weight decay超参数。默认情况下,PyTorch同时衰减权重和便宜。这里只为权重设置了weight_decay,所以偏置参数 b b b不会衰减。
def train_concise(wd):net = nn.Sequential(nn.Linear(num_inputs, 1))for param in net.parameters():param.data.normal_()loss = nn.MSELoss(reduction='none')num_epochs, lr = 100, 0.003# 偏置参数没有衰减trainer = torch.optim.SGD([{"params":net[0].weight,'weight_decay': wd},{"params":net[0].bias}], lr=lr)animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',xlim=[5, num_epochs], legend=['train', 'test'])for epoch in range(num_epochs):for X, y in train_iter:trainer.zero_grad()l = loss(net(X), y)l.mean().backward()trainer.step()if (epoch + 1) % 5 == 0:animator.add(epoch + 1,(d2l.evaluate_loss(net, train_iter, loss),d2l.evaluate_loss(net, test_iter, loss)))print('w的L2范数:', net[0].weight.norm().item())
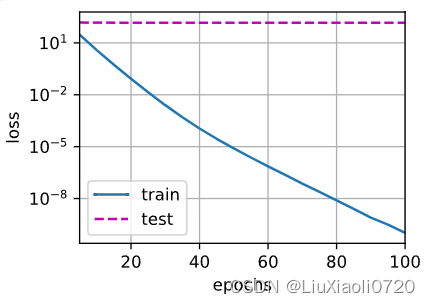
train_concise(0)
w的L2范数: 13.416662216186523
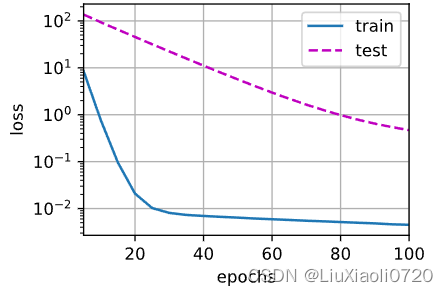
train_concise(3)
w的L2范数: 0.39273694157600403
相关文章:

【深度学习笔记】09 权重衰减
09 权重衰减 范数和权重衰减利用高维线性回归实现权重衰减初始化模型参数定义 L 2 L_2 L2范数惩罚定义训练代码实现忽略正则化直接训练使用权重衰减 权重衰减的简洁实现 范数和权重衰减 在训练参数化机器学习模型时,权重衰减(decay weight)…...

三大兼容 | 人大金仓兼容+优化MySQL用户变量特性
目前,KingbaseES对MySQL的兼容性,已从功能兼容阶段过渡到强性能兼容、生态全面兼容阶段,针对客户常常遇到的用户变量问题,KingbaseES在兼容MySQL用户变量功能的基础上,优化了MySQL用户变量的一些原生问题,使…...
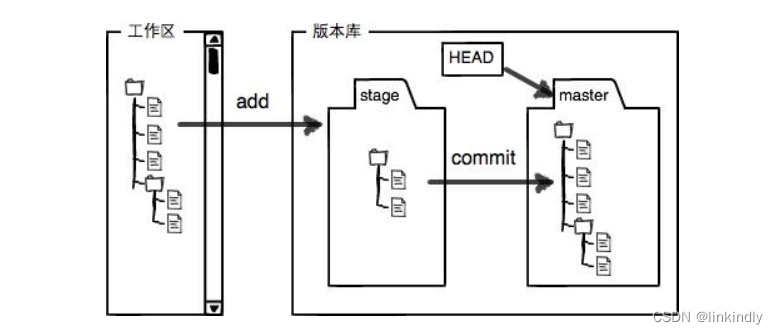
Git介绍与安装使用
目录 1.Git初识 1.1提出问题 1.2如何解决--版本控制器 1.3注意事项 2.Git安装 2.1Linux-centos安装 2.2Linux-ubuntu安装 2.3Windows安装 3.Git基本操作 3.1创建Git本地仓库 3.2配置Git 4.认识⼯作区、暂存区、版本库 1.Git初识 1.1提出问题 不知道你工作或学习时…...

理解DuLinkList L中的“”引用符号
在C中,DuLinkList &L 这种形式的参数表示 L 是一个 DuLinkList 类型的引用。这里的 & 符号表示引用。 引用是C的一个特性,它提供了一种方式来访问已存在的变量的别名。当你对引用进行操作时,实际上是在操作它所引用的变量。如果你在…...

前端并发多个请求并失败重发
const MAX_RETRIES 3;// 模拟请求 function makeRequest(url) {return new Promise((resolve, reject) > {setTimeout(() > {Math.random() < 0.75 ? resolve(${url} 成功) : reject(${url} 失败); // 随机决定请求是否成功}, Math.random() * 2000); // 随机延时执…...
【Qt开发流程】之对象模型2:属性系统
描述 Qt提供了一个复杂的属性系统,类似于一些编译器供应商提供的属性系统。然而,作为一个独立于编译器和平台的库,Qt不依赖于非标准的编译器特性,如__property或[property]。 Qt解决方案适用于Qt支持的所有平台上的任何标准c编译…...

PHP之curl详细讲解
cURL(全称为Client for URLs)是一个功能强大的开源库,用于在多种协议上进行数据传输、发送HTTP请求和获取响应。它支持多种协议,包括HTTP、HTTPS、FTP、SMTP等,并且能够与各种服务器进行通信。 cURL库可以通过命令行工…...
R语言30分钟上手
文章目录 1. 环境&安装1.1. rstudio保存工作空间 2. 创建数据集2.1. 数据集概念2.2. 向量、矩阵2.3. 数据框2.3.1. 创建数据框2.3.2. 创建新变量2.3.3. 变量的重编码2.3.4. 列重命名2.3.5. 缺失值2.3.6. 日期值2.3.7. 数据框排序2.3.8. 数据框合并(合并沪深300和中证500收盘…...
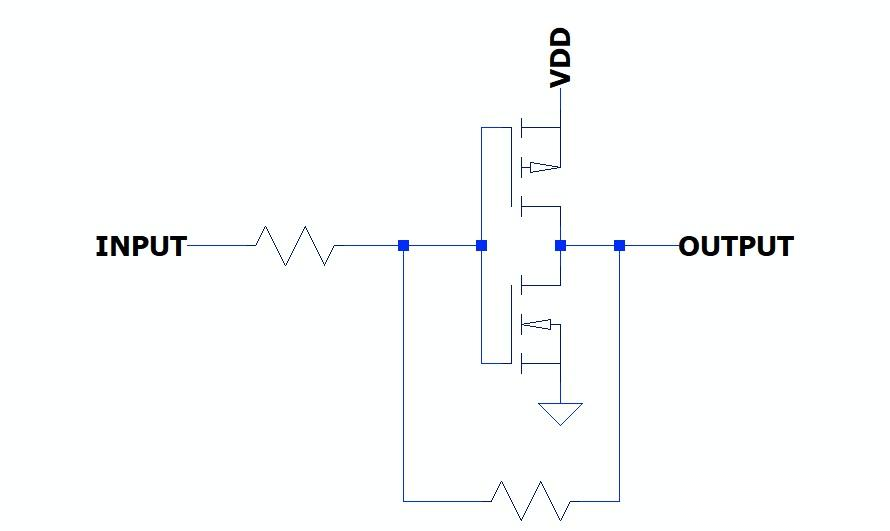
上下拉电阻会增强驱动能力吗?
最近看到一个关于上下拉电阻的问题,发现不少人认为上下拉电阻能够增强驱动能力。随后跟几个朋友讨论了一下,大家一致认为不存在上下拉电阻增强驱动能力这回事,因为除了OC输出这类特殊结构外,上下拉电阻就是负载,只会减…...

题目:小明的彩灯(蓝桥OJ 1276)
题目描述: 解题思路: 一段连续区间加减,采用差分。最终每个元素结果与0比较大小,比0小即负数输出0。 题解: #include<bits/stdc.h> using namespace std;using ll long long; const int N 1e5 10; ll a[N],…...

换元法求不定积分
1.一般步骤:选取换元对象(不一定是式子中的值,也可以是式子中的最小公倍数或者最大公因数),然后将dx换为dt*t的导数,再用t将原式表示,化简计算即可 2. 3. 4. 5. 6....

在Docker容器中启用SSH服务,实现外部访问的详细教程
目录 步骤 1: 安装 SSH 服务器 步骤 2: 配置 SSH 服务器 步骤 3: 设置 SSH 用户 步骤 4: 重启 SSH 服务器 步骤 5: 映射容器端口 步骤 6: 使用 SSH 连接到容器 要在Docker容器中启用SSH服务,以便从外部访问,您需要执行以下步骤: 步骤 …...

Go 模块系统最小版本选择法 MVS 详解
目录 Golang 模块系统简介 包版本管理 最小版本选择(MVS)原理 MVS 的优点 MVS的缺点 实际使用MVS 小结 参考资料 Golang 模块系统简介 Golang 模块系统是 Go 1.11 版本引入的一个新特性,主要目的是解决 Go 项目中的依赖管理问题。在模…...

ifstream读取txt中的中文数据转成QString出现乱码
使用ifstream从txt文本中读取中文数据到string,再将string转成QString输出时出现了乱码。 分析:如果ifstream能成功从txt文本中读出中文数据,那大概率txt用的编码是ANSI编码(GBK就是ANSI的一种),那么在转成…...
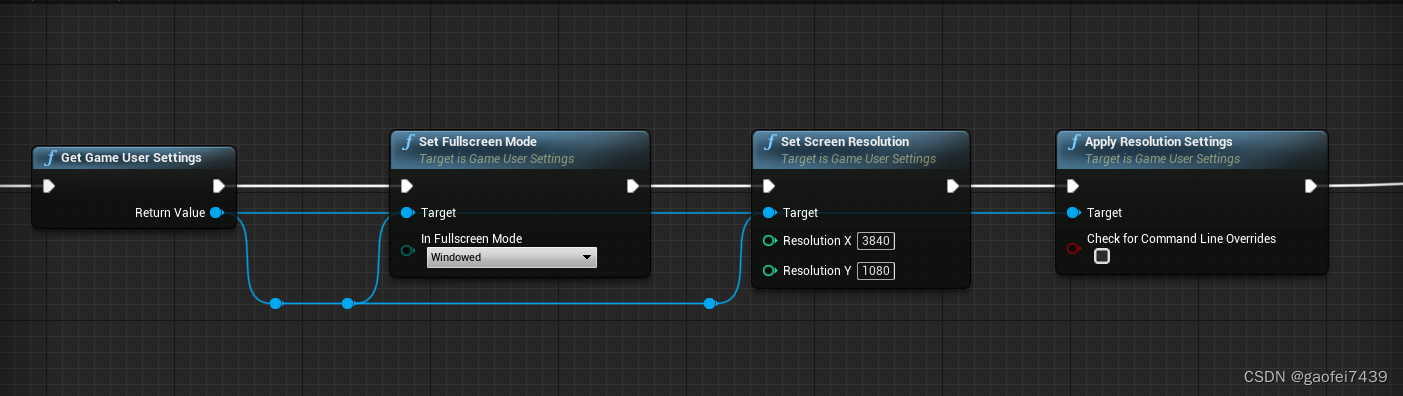
UE4 双屏分辨率设置
背景: 做了一个UI 应用,需要在双屏上进行显示。 分辨率如下:3840*1080; 各种折腾,其实很简单: 主要是在全屏模式的时候 一开始没有选对,双屏总是不稳定。 全屏模式改成:Windows 之…...

$sformat在仿真中打印文本名的使用
在仿真中,定义队列,使用任务进行函数传递,并传递文件名,传递队列,进行打印 $sformat(filename, “./data_log/%0d_%0d_%0d_0.txt”, f_num, lane_num,dt); 使用此函数可以自定义字符串,在仿真的时候进行文件…...

【Rust】结构体与枚举
文章目录 结构体struct基础用法使用字段初始化简写语法使用没有命名字段的元组结构体来创建不同的类型没有任何字段的类单元结构体方法语法关联函数多个 impl 块 枚举枚举值Option 结构体struct 基础用法 一个存储用户账号信息的结构体: struct User {active: bo…...

CentOS7 防火墙常用命令
以下是在 CentOS 7 上使用 firewall-cmd 命令管理防火墙时的一些常用命令: 检查防火墙状态: sudo firewall-cmd --state 启动防火墙: sudo systemctl start firewalld 停止防火墙: sudo systemctl stop firewalld 重启防火墙&…...

【无标题】什么是UL9540测试,UL9540:2023版本增加哪些测试项目
什么是UL9540测试,UL9540:2023版本增加哪些测试项目 UL 9540是美国安全实验室(Underwriters Laboratories)发布的标准,名称为"UL 9540: Energy Storage Systems and Equipment",翻译为中文为"能量存储…...
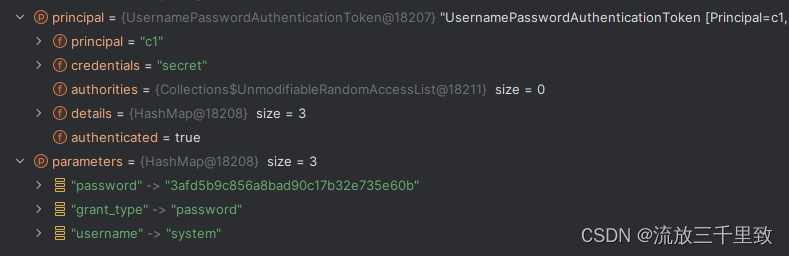
springcloud整合Oauth2自定义登录/登出接口
我使用的是password模式,并配置了token模式 一、登录 (这里我使用的示例是用户名密码认证方式) 1. Oath2提供默认登录授权接口 org.springframework.security.oauth2.provider.endpoint.postAccess; Tokenpublic ResponseEntity<OAuth2AccessToken> pos…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...
