[足式机器人]Part2 Dr. CAN学习笔记-数学基础Ch0-4线性时不变系统中的冲激响应与卷积
本文仅供学习使用
本文参考:
B站:DR_CAN
Dr. CAN学习笔记-数学基础Ch0-4线性时不变系统中的冲激响应与卷积
- 1. LIT System:Linear Time Invariant
- 2. 卷积 Convolution
- 3. 单位冲激 Unit Impulse——Dirac Delta
线性时不变系统 : LIT System
冲激响应:Impluse Response
卷积:Convolution
1. LIT System:Linear Time Invariant
-
运算operator : O { ⋅ } O\left\{ \cdot \right\} O{⋅}
I n p u t O { f ( t ) } = o u t p u t x ( t ) \begin{array}{c} Input\\ O\left\{ f\left( t \right) \right\}\\ \end{array}=\begin{array}{c} output\\ x\left( t \right)\\ \end{array} InputO{f(t)}=outputx(t) -
线性——
叠加原理superpositin principle:
{ O { f 1 ( t ) + f 2 ( t ) } = x 1 ( t ) + x 2 ( t ) O { a f 1 ( t ) } = a x 1 ( t ) O { a 1 f 1 ( t ) + a 2 f 2 ( t ) } = a 1 x 1 ( t ) + a 2 x 2 ( t ) \begin{cases} O\left\{ f_1\left( t \right) +f_2\left( t \right) \right\} =x_1\left( t \right) +x_2\left( t \right)\\ O\left\{ af_1\left( t \right) \right\} =ax_1\left( t \right)\\ O\left\{ a_1f_1\left( t \right) +a_2f_2\left( t \right) \right\} =a_1x_1\left( t \right) +a_2x_2\left( t \right)\\ \end{cases} ⎩ ⎨ ⎧O{f1(t)+f2(t)}=x1(t)+x2(t)O{af1(t)}=ax1(t)O{a1f1(t)+a2f2(t)}=a1x1(t)+a2x2(t) -
时不变Time Invariant:
O { f ( t ) } = x ( t ) ⇒ O { f ( t − τ ) } = x ( t − τ ) O\left\{ f\left( t \right) \right\} =x\left( t \right) \Rightarrow O\left\{ f\left( t-\tau \right) \right\} =x\left( t-\tau \right) O{f(t)}=x(t)⇒O{f(t−τ)}=x(t−τ)
2. 卷积 Convolution

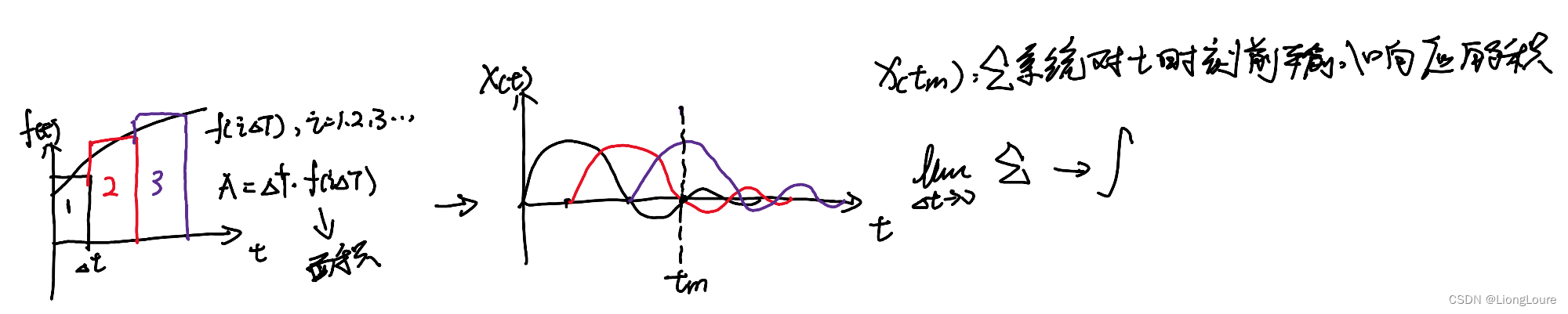
3. 单位冲激 Unit Impulse——Dirac Delta
LIT系统,h(t)可以完全定义系统

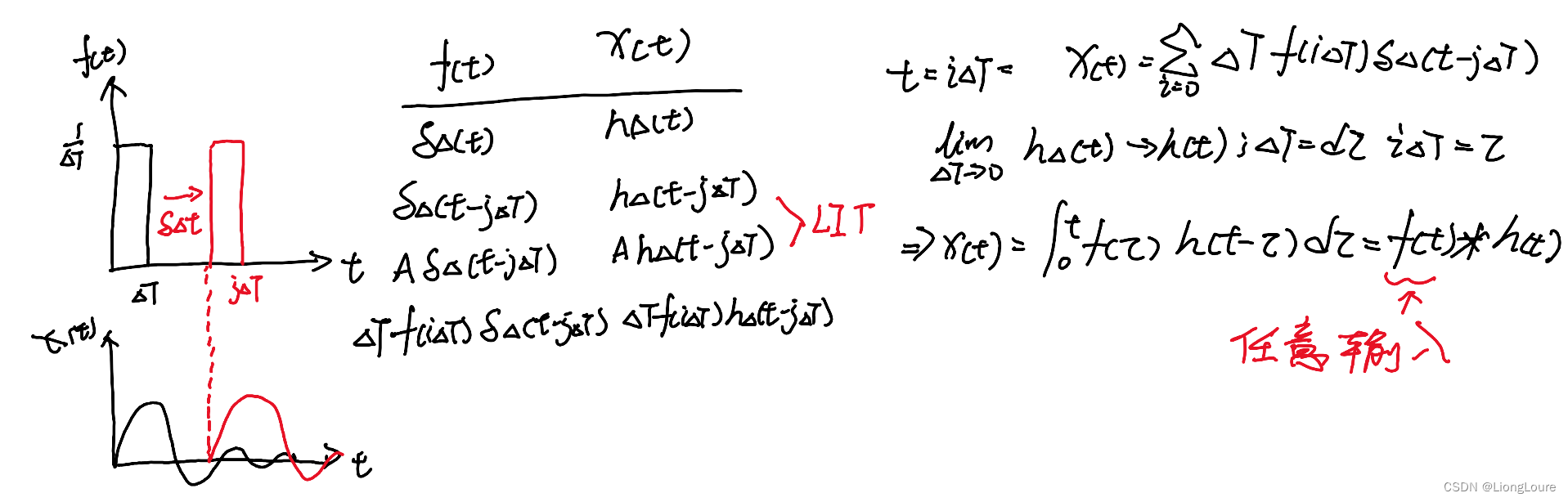
相关文章:
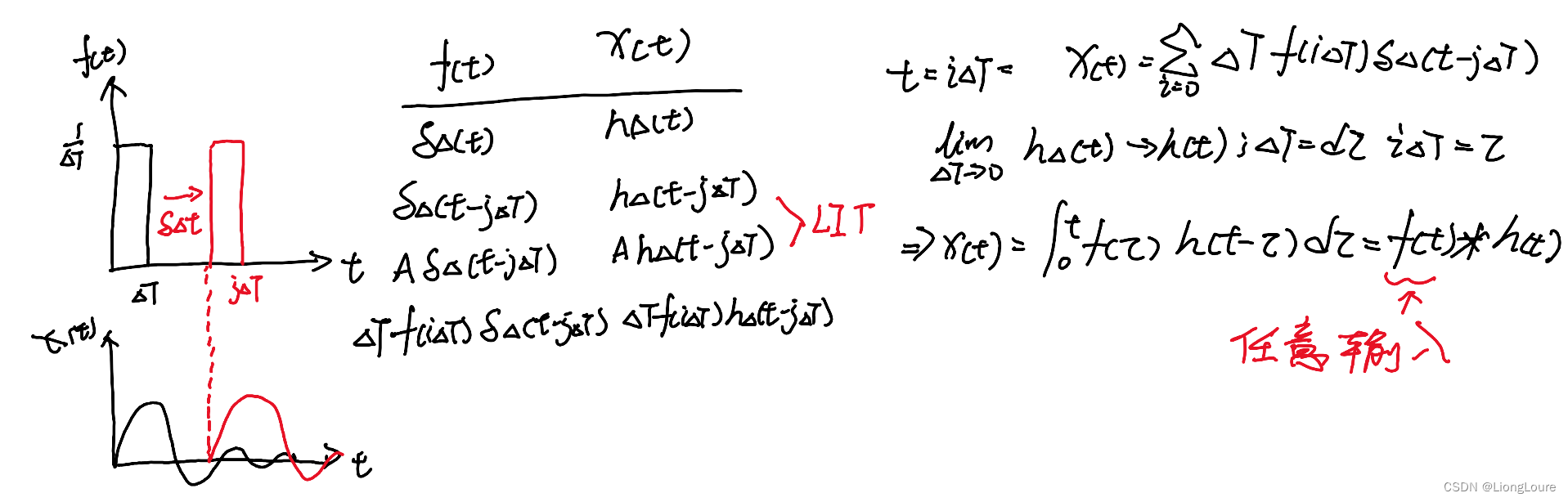
[足式机器人]Part2 Dr. CAN学习笔记-数学基础Ch0-4线性时不变系统中的冲激响应与卷积
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记-数学基础Ch0-4线性时不变系统中的冲激响应与卷积 1. LIT System:Linear Time Invariant2. 卷积 Convolution3. 单位冲激 Unit Impulse——Dirac Delta 线性时不变系统 : L…...

CSS BFC特性和应用
目录 1,介绍2,BFC布局规则3,创建BFC4,BFC应用1,浮动子元素使父级高度坍塌2,非浮动元素被浮动元素覆盖3,margin 合并1,父子 margin 合并:父级和第1个/最后1个子元素2&…...
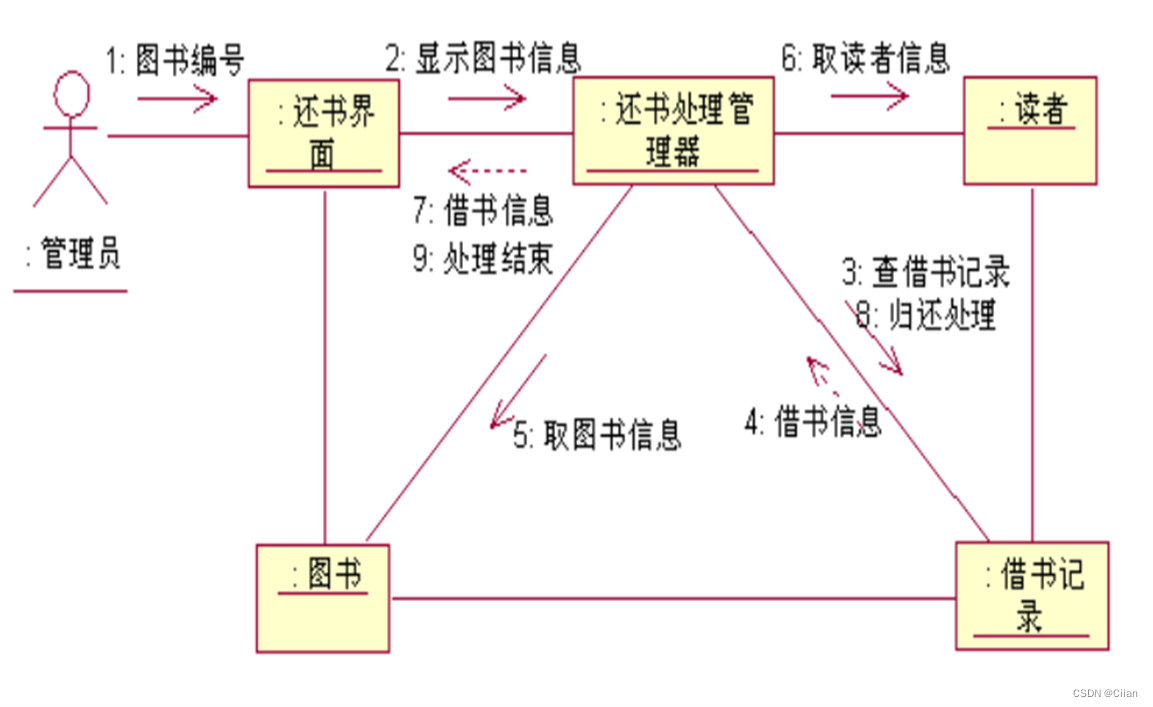
软件工程 - 第8章 面向对象建模 - 3 - 动态建模
状态图 状态是指在对象生命周期中满足某些条件、执行某些活动或等待某些事件的一个条件和状况 。 案例一:描述烧水器在工作时的详细行为细节 “人就是一个类,而你”、我”、张三”等都是“人这个类的一个实例,站着”、“躺着等都是对象的一…...

Stable Diffusion AI绘画系列【16】:霸气侧漏的二次元武侠风
《博主简介》 小伙伴们好,我是阿旭。专注于人工智能、AIGC、python、计算机视觉相关分享研究。 ✌更多学习资源,可关注公-仲-hao:【阿旭算法与机器学习】,共同学习交流~ 👍感谢小伙伴们点赞、关注! 《------往期经典推…...
第二证券:苹果市值重返3万亿美元,关键因素并非人工智能
当地时间12月5日,到美股收盘,苹果公司股价收涨2.1%,报193.42美元,收盘市值重返3万亿美元上方。 上一年12月,苹果公司市值曾在盘中时间短触及3万亿门槛,但收盘并未站稳,本年6月收盘时正式打破3万…...

西南科技大学C++程序设计实验六( 继承与派生一)
一、实验目的 1. 理解不同继承属性对派生类访问基类成员的区别 2. 掌握单继承程序编写 二、实验任务 1、调试下列程序,并在对程序进行修改后再调试,指出调试中的出错原因(该题中A为基类,B为派生类,B以public方式继承A) 重点:理解不同继承方式数据的访问权限,派生类…...
MySQL 性能优化
未完待续... 1. 分库、分表结构优化 1.1 数据库设计 不规范的数据库设计存在数据冗余以及插入、更新、删除异常问题。 规范化(Normalization)是数据库设计的一系列原理和技术,主要用于减少表中数据的冗余,增加完整性和一致性&…...

求职招聘小程序源码系统 全开源源代码:找工作+招人才 平台级别运营版 附带完整的搭建教程
在当前的求职招聘市场中,尽管存在大量的求职者和招聘者,但依然存在着信息不对称、沟通不畅等问题。小编来给大家分享一款求职招聘小程序源码系统,旨在提供一个高效、便捷、安全的求职招聘平台。 以下是部分代码示例: 系统特色功能…...

26、卷积 - 实际上是一个特征提取器
矩阵乘法的本质是特征的融合,卷积算法的本质是特征的提取。 回想一下之前所有介绍卷积的时候,描述了一种卷积运算的场景,那就是一个窗口在图片上滑动,窗口中的数值是卷积核的参数,也就是权值。 卷积的计算本质是乘累…...

web前端之vue3
MENU vue3响应式数据的判断、isRef、isReactive、isReadonly、isProxy、ref、reactive、readonlyvue3的生命周期vue3手写isRef、isReactive、isReadonly、isProxyvue3手写ref、深的refvue3手写shallowRef、浅的refvue3customRefvue3readonly与shallowReadonlyvue3toRaw与markRa…...

原来在C++的类中声明函数时可以不写参数名只写参数类型
2023年12月6日,周三上午 今天才发现原来可以这样写 在C的类中声明函数时可以不写参数名只写参数类型, 但是,在实现时必须写出参数名。 #include<iostream>class People { public:void move(int);void say(std::string);void doSomet…...

独孤思维:这里有蓝海项目,你要吗?
很多人,一看到蓝海项目,就趋之若鹜。 觉得红海项目太卷了,根本赚不到钱。 凡是认为蓝海项目不卷,可以做起来,做的轻松的,都是弱智和无能的表现。 你所能接触到的蓝海,根本就不是蓝海。 能够…...

外卖平台推荐算法的优化与实践
目录 引言 一、推荐算法的原理 二、推荐算法的挑战 三、实际案例分析 四、优化推荐算法的策略 五、结论 引言 在当今数字化社会,外卖平台成为了人们生活中不可或缺的一部分。为了提供更加个性化、高效的服务,外卖平台使用推荐算法成为了一项关键技…...

CONTROLLING VISION-LANGUAGE MODELS FOR MULTI-TASK IMAGE RESTORATION
CONTROLLING VISION-LANGUAGE MODELS FOR MULTI-TASK IMAGE RESTORATION (Paper reading) Ziwei Luo, Uppsala University, ICLR under review(6663), Cited:None, Stars: 350, Code, Paper. 1. 前言 像CLIP这样的视觉语言模型已经显示出对零样本或无标签预测的各种下游任务…...

HarmonyOS应用开发——页面
我们将对于多页面以及更多有趣的功能展开叙述,这次我们对于 HarmonyOS 的很多有趣常用组件并引出一些其他概念以及解决方案、页面跳转传值、生命周期、启动模式(UiAbility),样式的书写、状态管理以及动画等方面进行探讨 页面之间…...
)
Java流Stream使用详解(练习)
练习 第一题 数据过滤 定义一个集合,并添加一些整数1,2,3,4,5,6,7,8,9,10过滤奇数,只留下偶数,并将结果保存起来 import java.util.ArrayList; import java.util.Collections; import java.util.List; import java.util.stream.Collectors…...

请介绍一下MySQL的存储引擎及其特点
问题:请介绍一下MySQL的存储引擎及其特点。 回答: MySQL是一个开源的关系型数据库管理系统,它支持多种存储引擎,每个存储引擎都有其自身的特点和适用场景。下面是对MySQL常见存储引擎的简要介绍: InnoDB: …...

Python---魔术方法
1、什么是魔术方法 在Python中,__xxx__()的函数叫做魔法方法,指的是具有特殊功能的函数。 2、__init__()方法(初始化方法或构造方法) 思考:人的姓名、年龄等信息都是与生俱来的属性,可不可以在生产过程中就赋予这些属性呢&…...

手把手教你注册意大利商标
在当今全球商业环境中,拥有一个独特的商标可以为企业在市场竞争中提供重要优势。商标作为品牌形象的核心,有助于吸引潜在客户,提升品牌价值,增加客户忠诚度。在意大利,商标注册同样具有重要意义,它能为企业…...

pandas详细笔记
一:什么是Pandas from matplotlib import pyplot import numpy as np import pandas as pdarange np.arange(1, 10, 2) series pd.Series(arange,indexlist("ABCDE")) print(series)二:索引 三:切片 位置索引切片(左闭…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
