在开发软件KEIL MDK和IAR开发工程里面打印行号、文件名、函数名、时间
最近应用固件没有时间记录,分别请那个是最新的(在没有版本区别的情况下),有个办法记录编译时间即可,记录笔记以便查看
在软件工程里面直接用宏
__FILE __ 当前程序文件名的字符串
__FUNCTION __ 当前函数的名字字符串
__LINE __ 当前行数整型
__TATE __ 当前日期
__TIME __ 当前时间
测试一下例题,如下
void AppWritedToFlash(void)
{printf("\n*********************************************************\n"); printf("Time:%s%s\nfuncName:%s\nLine:%d\n",__DATE__,__TIME__,__FUNCTION__,__LINE__);printf("OTA executed now \r\n");printf("pragraming....\r\n");printf("\n*********************************************************\n"); }
串口助手打印信息如下
*********************************************************
Time:Dec 6 2023 17:34:57
funcName:AppWritedToFlash
Line:170
OTA executed now
pragraming....*********************************************************
相关文章:

在开发软件KEIL MDK和IAR开发工程里面打印行号、文件名、函数名、时间
最近应用固件没有时间记录,分别请那个是最新的(在没有版本区别的情况下),有个办法记录编译时间即可,记录笔记以便查看 在软件工程里面直接用宏 __FILE __ 当前程序文件名的字符串 __FUNCTION __ 当前函数的名字字符串 …...
)
springboot(ssm健身器材用品网 健身用品商城Java(codeLW)
springboot(ssm必录德健身器材用品网 健身用品商城Java(code&LW) 开发语言:Java 框架:ssm/springboot vue JDK版本:JDK1.8(或11) 服务器:tomcat 数据库:mysql 5.7(或8.0&am…...

idea git合并推送分支
远端代码合并到当前分支 1.本地切换到当前分支 2.远端目标分支右键合并到当前分支(使用合并拉入) 本地当前分支推送合并到远端分支 1.切换到远端本地分支 2.合并本地其他分支(想要推送的分支)到当前分支 3.推送分支 注意:这里的合并是:将XXX合并到XXX中 …...
AntDesignBlazor示例——创建列表页
本示例是AntDesign Blazor的入门示例,在学习的同时分享出来,以供新手参考。 示例代码仓库:https://gitee.com/known/AntDesignDemo 1. 学习目标 使用Table组件创建列表页面使用DisplayName特性显示中文表头使用模板和Tag组件显示高温数据使…...
微信小程序模板选择指南:如何找到靠谱的平台?
随着移动互联网的快速发展,越来越多的企业和商家都在微信小程序上开展业务。而他们也希望可以通过微信小程序模板快速搭建小程序,那么如何才能找到一个靠谱的微信小程序模板平台呢?下面给大家简单讲解一下。 首先要知道的是,微信小…...

es常用查询编辑
查询指定id信息 GET /index_name/_doc/1074266245查询指定信息并降序 GET /index_name/_search {"query": {"term": {"deviceId": {"value": "1074266245"}}}, "sort": [{"timestamp": {"order&qu…...

记录 | linux静态库和动态库的理解
hello.cpp: #include <cstdio>void hello() {printf("Hello, world!\n"); }main.cpp: #include <cstdio>void hello();int main() {hello();return 0; }静态库编译配置: cmake_minimum_required(VERSION 3.12) proj…...
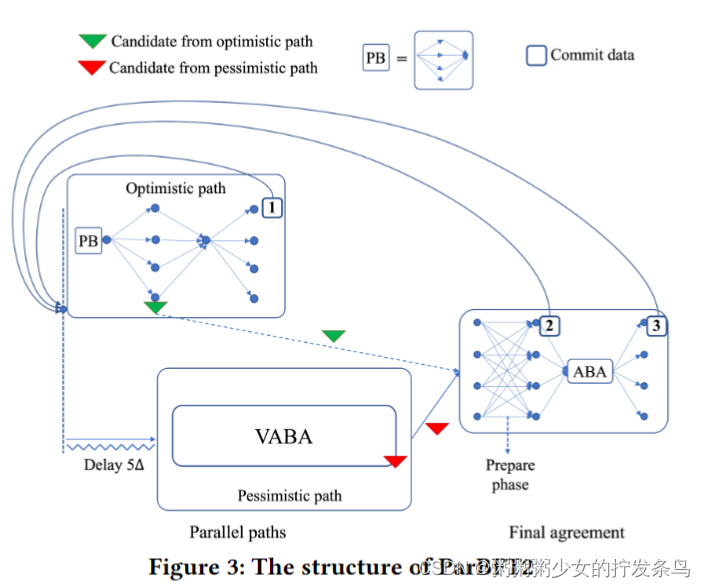
ParBFT: Faster Asynchronous BFT Consensus with a Parallel Optimistic Path
目录 笔记后续的研究方向摘要引言 ParBFT: Faster Asynchronous BFT Consensus with a Parallel Optimistic Path CCS 2023 笔记 后续的研究方向 摘要 为了减少异步拜占庭容错(BFT)共识的延迟和通信开销,通常会添加一条乐观的路径…...

java小工具util系列3:JSON转实体类对象工具
文章目录 准备工作1.JSONObject获取所有的key2.集合中实体对象转换 list中Enrey转Dto3.字符串转List<BusyTimeIndicatorAlarmThreshold>4.json字符串转JSONObject5.list根据ids数组过滤list6.json字符串转JavaBean对象7.json对象转javabean8.jsonObject转map9.List\<U…...
MySQL:找回root密码
一、情景描述 我们在日常学习中,经常会忘记自己的虚拟机中MySQL的root密码。 这个时候,我们要想办法重置root密码,从而,解决root登陆问题。 二、解决办法 1、修改my.cnf配置文件并重启MySQL 通过修改配置文件,来跳…...
计算机网络扫盲(1)——因特网
一、概述 因特网是一个世界范围的计算机网络,即它是一个互联了遍及全世界数十亿计算设备的网络。大家对此应该并不陌生,我们身边有着不计其数的计算机设备被接入了因特网,如今计算机网络这个术语似乎已经有点过时了,用因特网的术语…...
分号问题)
C语言 if语句有无(;)分号问题
在C语言中,if语句后面不带分号(;)的情况有两种主要形式: 1. 带有大括号的代码块:如果if语句后面跟随一个由大括号({})包围的代码块,那么这个代码块中的语句只有在if条件为真时才会执…...
)
Python-列表详解(列表的创建、用法、遍历、注意事项、特点等)
本文有以下内容: 列表的创建 列表的下标索引注意事项 列表的访问 列表的增加元素 列表的删除元素 列表的任意删除元素 列表的查找元素 列表的查找元素位置 列表的插入任意位置 列表的遍历 列表的拼接方式 列表的切片操作以及注意事项 列表类似于其他语言的数组 列…...
【langchain实战】开源项目-RasaGPT
1、概述 RasaGpt是一个建立在 Rasa 和 Langchain 之上的没有显示界面的LMM聊天机器人平台。它是一个Rasa和Telegram这种利用像Langchain这样的LMM库进行索引、检索和上下文注入的样板及参考实现。 开源地址: GitHub - paulpierre/RasaGPT: 💬 RasaGPT is…...
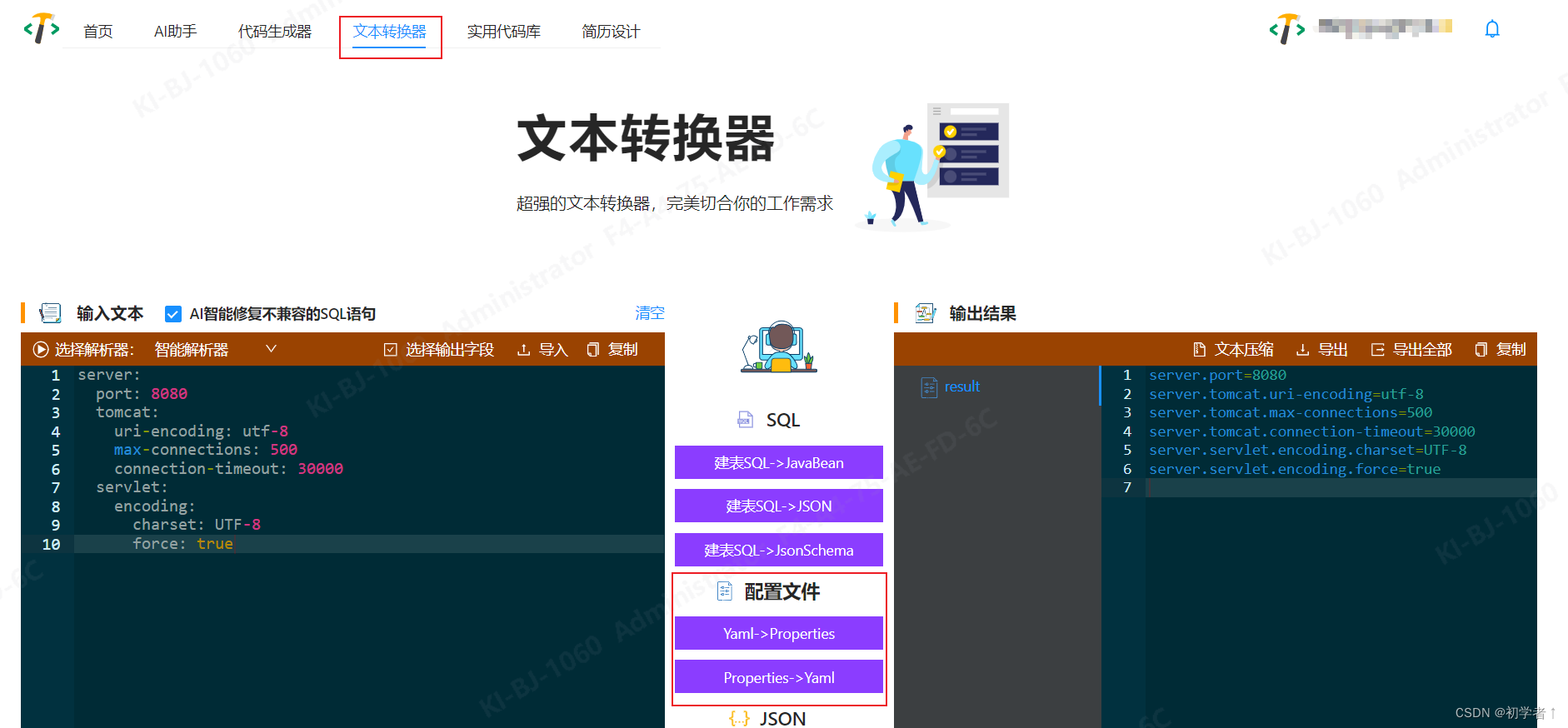
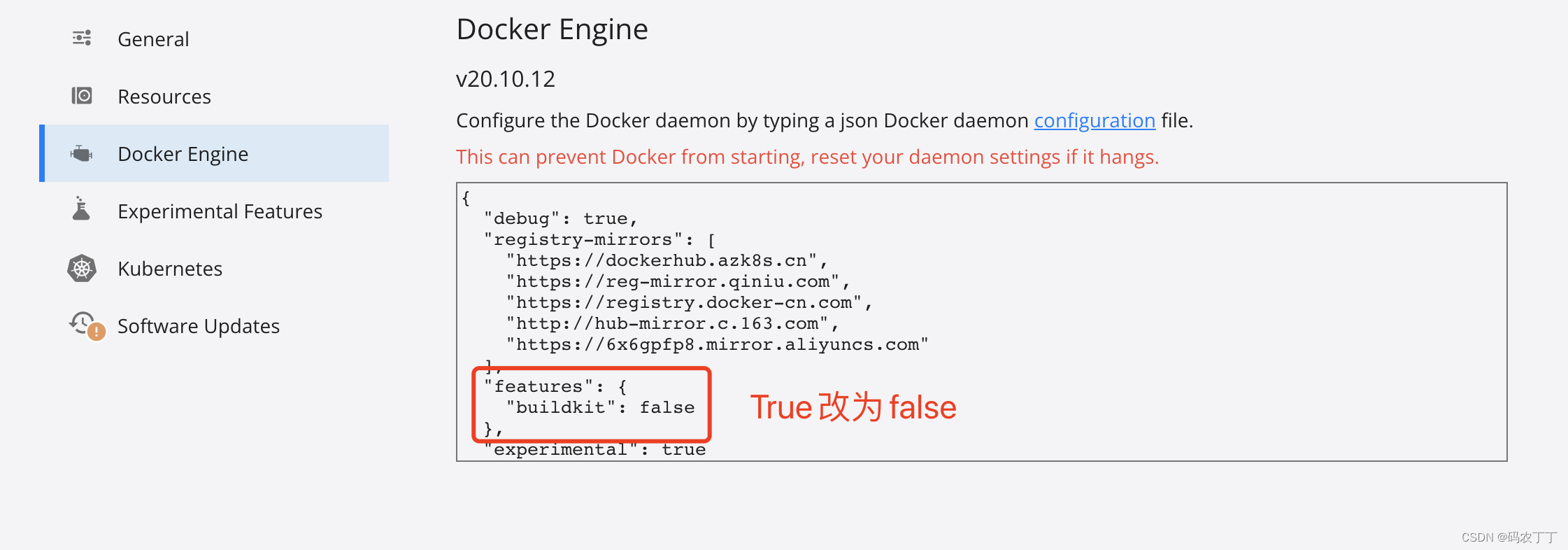
在线yml和properties相互转换
目前搜索到的大部分代码都存在以下问题: 复杂结构解析丢失解析后顺序错乱 所以自己写了一个,经过不充分测试,基本满足使用。可以直接在线使用 在线地址 除了yml和properties互转之外,还可以生成代码、sql转json等,可…...
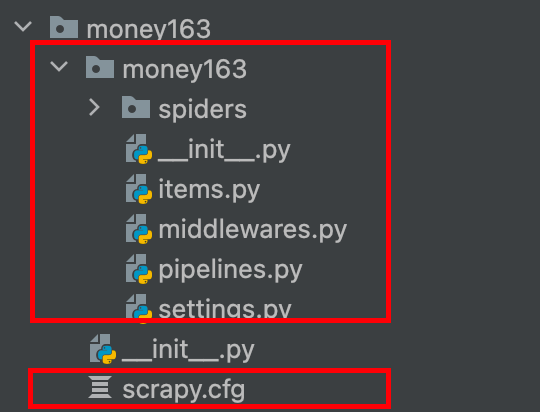
数据收集与处理(爬虫技术)
文章目录 1 前言2 网络爬虫2.1 构造自己的Scrapy爬虫2.1.1 items.py2.1.2 spiders子目录2.1.3 pipelines.py 2.2 构造可接受参数的Scrapy爬虫2.3 运行Scrapy爬虫2.3.1 在命令行运行2.3.2 在程序中调用 2.4 运行Scrapy的一些要点 3 大规模非结构化数据的存储与分析4 全部代码 1 …...
C# 雪花算法生成Id工具类
写在前面 传说自然界中并不存在两片完全一样的雪花的,每一片雪花都拥有自己漂亮独特的形状、独一无二;雪花算法也表示生成的ID如雪花般独一无二,该算法源自Twitter。 雪花算法主要用于解决分布式系统的唯一Id生成问题,在生产环境…...
什么是通配符证书?
通配符证书是一种特殊的数字证书,主要用于加密网站与用户之间的通信,以保证数据的私密性和完整性。它的独特之处在于可以使用一个单一的证书来保护无限数量的相关子域名。它使用通配符字符(*)作为占位符,代表任意子域名…...
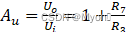
西南科技大学模拟电子技术实验五(集成运算放大器的应用设计)预习报告
一、计算/设计过程 设计一:用集成运放设计一个输入为0.05v,放大为-100的反相比例运算电路。 对于理想电路,反相比例运算电路的输出电压与输入电压之间的关系如下: =-100,所以 =100 若是假定R1为100k,则R2= =1k 为了减小输入级偏置电流引起的运算误差,在同相输入端…...
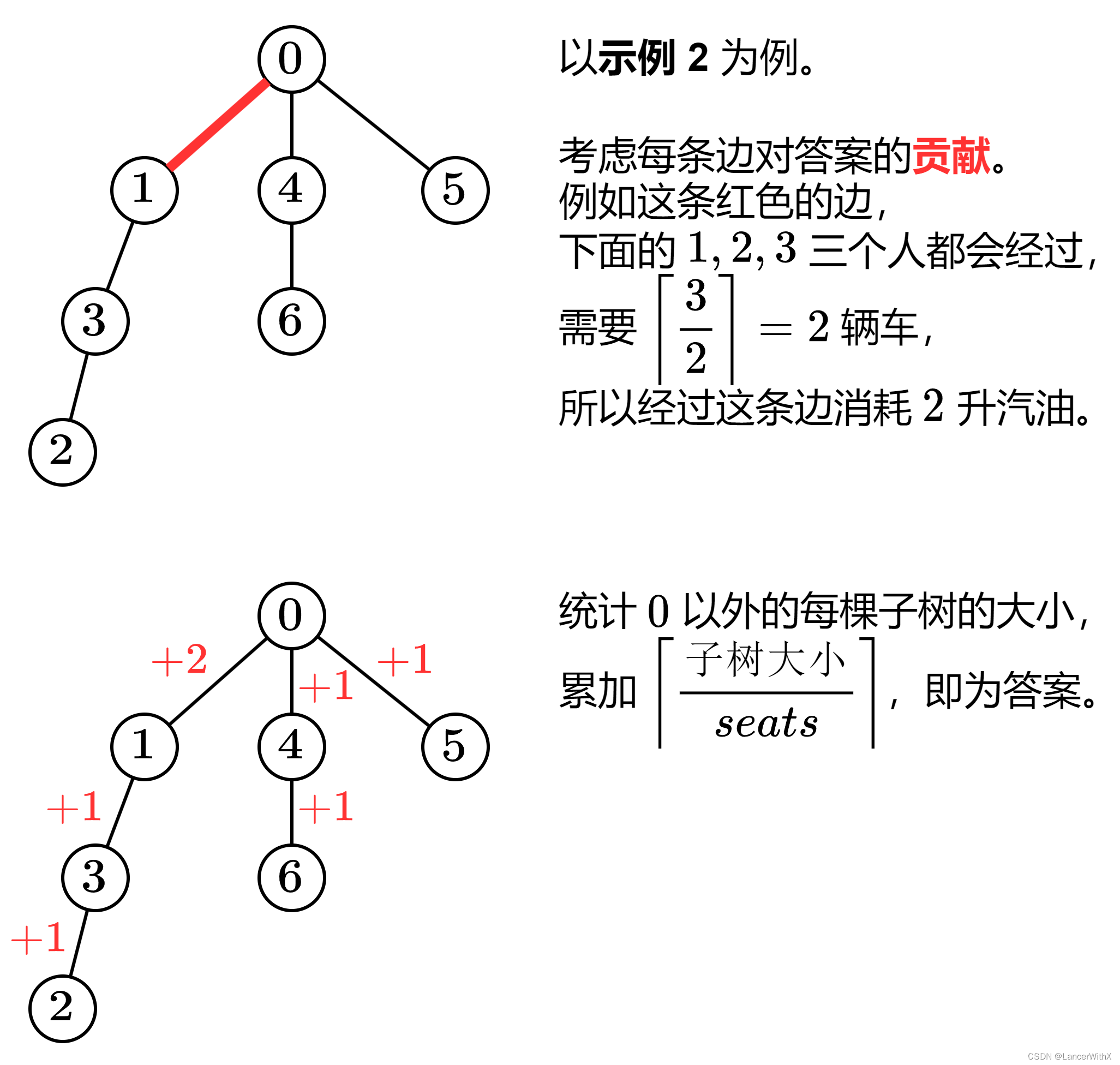
LeetCode 每日一题 Day 4
2477. 到达首都的最少油耗 给你一棵 n 个节点的树(一个无向、连通、无环图),每个节点表示一个城市,编号从 0 到 n - 1 ,且恰好有 n - 1 条路。0 是首都。给你一个二维整数数组 roads ,其中 roads[i] [ai,…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...
