使用Pytoch实现Opencv warpAffine方法
随着深度学习的不断发展,GPU/NPU的算力也越来越强,对于一些传统CV计算也希望能够直接在GPU/NPU上进行,例如Opencv的warpAffine方法。Opencv的warpAffine的功能主要是做仿射变换,如果不了解仿射变换的请自行了解。由于Pytorch的图像坐标系(图像左上角对应坐标(-1, -1)右下角对应坐标(1, 1))与Opencv的坐标系(图像左上角对应坐标(0, 0)右下角对应坐标(w - 1, h - 1))有差异,故无法直接使用Opencv的warp矩阵对Pytorch数据进行变换。
主要参考文章:https://zhuanlan.zhihu.com/p/349741938
本文逻辑推理部分主要是参照上述的参考文章,这里再简单推导一遍。后面会给出基于该公式推导的Pytorch实现。
下面公式简单介绍了原始图片中 ( x 1 , y 1 ) (x_1, y_1) (x1,y1)点通过仿射变化到输出图片 ( x 2 , y 2 ) (x_2, y_2) (x2,y2)点的过程,假设 ( x , y ) (x, y) (x,y)对应Opencv图像坐标系。
[ x 2 y 2 1 ] = [ a b c d e f 0 0 1 ] [ x 1 y 1 1 ] \begin{bmatrix} x_2\\ y_2 \\ 1 \end{bmatrix} = \begin{bmatrix} a & b & c\\ d & e & f\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_1\\ y_1 \\ 1 \end{bmatrix} x2y21 = ad0be0cf1 x1y11
现在要将Opencv图像坐标系下的 ( x 1 , y 1 ) (x_1, y_1) (x1,y1)点映射到Pytorch的图像坐标系下 ( u 1 , v 1 ) (u_1, v_1) (u1,v1)点,由于Pytorch的图像坐标系是从-1到1,所以对Opencv的坐标做如下变化即可。注,由于Opencv坐标从0开始,所以对于原图宽为src_w,高为src_h实际右下角的坐标应该是 ( s r c w − 1 , s r c h − 1 ) (src_w - 1, src_h - 1) (srcw−1,srch−1)。
u 1 = x 1 − s r c w − 1 2 s r c w − 1 2 = 2 x 1 s r c w − 1 − 1 u_1 = \frac{x_1 - \frac{src_w - 1}{2} }{\frac{src_w - 1}{2}} = \frac{2x_1}{src_w - 1} -1 u1=2srcw−1x1−2srcw−1=srcw−12x1−1
v 1 = y 1 − s r c h − 1 2 s r c h − 1 2 = 2 y 1 s r c h − 1 − 1 v_1 = \frac{y_1 - \frac{src_h - 1}{2} }{\frac{src_h - 1}{2}} = \frac{2y_1}{src_h - 1} -1 v1=2srch−1y1−2srch−1=srch−12y1−1
写成矩阵乘的形式:
[ u 1 v 1 1 ] = [ 2 s r c w − 1 0 − 1 0 2 s r c h − 1 − 1 0 0 1 ] [ x 1 y 1 1 ] \begin{bmatrix} u_1\\ v_1 \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{2}{src_w - 1} & 0 & -1\\ 0 & \frac{2}{src_h - 1} & -1\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_1\\ y_1 \\ 1 \end{bmatrix} u1v11 = srcw−12000srch−120−1−11 x1y11
那么同理将仿射变化后Opencv图像坐标系下的 ( x 2 , y 2 ) (x_2, y_2) (x2,y2)点映射到Pytorch的图像坐标系下 ( u 2 , v 2 ) (u_2, v_2) (u2,v2)点,其中dst_w为仿射变化后输出图片的宽度,dst_h为仿射变化后输出图片的高度:
[ u 2 v 2 1 ] = [ 2 d s t w − 1 0 − 1 0 2 d s t h − 1 − 1 0 0 1 ] [ x 2 y 2 1 ] \begin{bmatrix} u_2\\ v_2 \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{2}{dst_w - 1} & 0 & -1\\ 0 & \frac{2}{dst_h - 1} & -1\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x_2\\ y_2 \\ 1 \end{bmatrix} u2v21 = dstw−12000dsth−120−1−11 x2y21
然后将上面两个公式代入最开始的仿射变化公式中:
[ 2 d s t w − 1 0 − 1 0 2 d s t h − 1 − 1 0 0 1 ] − 1 [ u 2 v 2 1 ] = [ a b c d e f 0 0 1 ] [ 2 s r c w − 1 0 − 1 0 2 s r c h − 1 − 1 0 0 1 ] − 1 [ u 1 v 1 1 ] \begin{bmatrix} \frac{2}{dst_w - 1} & 0 & -1\\ 0 & \frac{2}{dst_h - 1} & -1\\ 0 & 0 & 1 \end{bmatrix}^{-1} \begin{bmatrix} u_2\\ v_2 \\ 1 \end{bmatrix} = \begin{bmatrix} a & b & c\\ d & e & f\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \frac{2}{src_w - 1} & 0 & -1\\ 0 & \frac{2}{src_h - 1} & -1\\ 0 & 0 & 1 \end{bmatrix}^{-1} \begin{bmatrix} u_1\\ v_1 \\ 1 \end{bmatrix} dstw−12000dsth−120−1−11 −1 u2v21 = ad0be0cf1 srcw−12000srch−120−1−11 −1 u1v11
整理得到:
[ u 2 v 2 1 ] = [ 2 d s t w − 1 0 − 1 0 2 d s t h − 1 − 1 0 0 1 ] [ a b c d e f 0 0 1 ] [ 2 s r c w − 1 0 − 1 0 2 s r c h − 1 − 1 0 0 1 ] − 1 [ u 1 v 1 1 ] \begin{bmatrix} u_2\\ v_2 \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{2}{dst_w - 1} & 0 & -1\\ 0 & \frac{2}{dst_h - 1} & -1\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} a & b & c\\ d & e & f\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \frac{2}{src_w - 1} & 0 & -1\\ 0 & \frac{2}{src_h - 1} & -1\\ 0 & 0 & 1 \end{bmatrix}^{-1} \begin{bmatrix} u_1\\ v_1 \\ 1 \end{bmatrix} u2v21 = dstw−12000dsth−120−1−11 ad0be0cf1 srcw−12000srch−120−1−11 −1 u1v11
引用参考文章中大佬的原话,这个暂时没在Pytorch官方文档中找到,但是通过实验,确实如此。
affine_grid定义为目标图到原图的变换
所以,Pytorch中使用的theta实际是从 ( u 2 , v 2 ) (u_2, v_2) (u2,v2)到 ( u 1 , v 1 ) (u_1, v_1) (u1,v1)的矩阵:
[ u 1 v 1 1 ] = [ 2 s r c w − 1 0 − 1 0 2 s r c h − 1 − 1 0 0 1 ] [ a b c d e f 0 0 1 ] − 1 [ 2 d s t w − 1 0 − 1 0 2 d s t h − 1 − 1 0 0 1 ] − 1 [ u 2 v 2 1 ] \begin{bmatrix} u_1\\ v_1 \\ 1 \end{bmatrix} = \begin{bmatrix} \frac{2}{src_w - 1} & 0 & -1\\ 0 & \frac{2}{src_h - 1} & -1\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} a & b & c\\ d & e & f\\ 0 & 0 & 1 \end{bmatrix}^{-1} \begin{bmatrix} \frac{2}{dst_w - 1} & 0 & -1\\ 0 & \frac{2}{dst_h - 1} & -1\\ 0 & 0 & 1 \end{bmatrix}^{-1} \begin{bmatrix} u_2\\ v_2 \\ 1 \end{bmatrix} u1v11 = srcw−12000srch−120−1−11 ad0be0cf1 −1 dstw−12000dsth−120−1−11 −1 u2v21
故Opencv使用的theta到Pytorch的theta变换过程如下:
t h e t a ( p y t o r c h ) = [ 2 s r c w − 1 0 − 1 0 2 s r c h − 1 − 1 0 0 1 ] t h e t a ( o p e n c v ) − 1 [ 2 d s t w − 1 0 − 1 0 2 d s t h − 1 − 1 0 0 1 ] − 1 theta_{(pytorch)} = \begin{bmatrix} \frac{2}{src_w - 1} & 0 & -1\\ 0 & \frac{2}{src_h - 1} & -1\\ 0 & 0 & 1 \end{bmatrix} {theta}^{-1}_{(opencv)} \begin{bmatrix} \frac{2}{dst_w - 1} & 0 & -1\\ 0 & \frac{2}{dst_h - 1} & -1\\ 0 & 0 & 1 \end{bmatrix}^{-1} theta(pytorch)= srcw−12000srch−120−1−11 theta(opencv)−1 dstw−12000dsth−120−1−11 −1
最后给出对应代码实现:
"""
pip install numpy
pip install opencv-python
pip install opencv-python-headless
"""
import numpy as np
import cv2
import torch
import torch.nn.functional as Fdef cal_torch_theta(opencv_theta: np.ndarray, src_h: int, src_w: int, dst_h: int, dst_w: int):m = np.concatenate([opencv_theta, np.array([[0., 0., 1.]], dtype=np.float32)])m_inv = np.linalg.inv(m)a = np.array([[2 / (src_w - 1), 0., -1.],[0., 2 / (src_h - 1), -1.],[0., 0., 1.]], dtype=np.float32)b = np.array([[2 / (dst_w - 1), 0., -1.],[0., 2 / (dst_h - 1), -1.],[0., 0., 1.]], dtype=np.float32)b_inv = np.linalg.inv(b)pytorch_m = a @ m_inv @ b_invreturn torch.as_tensor(pytorch_m[:2], dtype=torch.float32)def main():img_bgr = cv2.imread("1.png")src_h, src_w, _ = img_bgr.shapeprint(f"src image h:{src_h}, w:{src_w}")dst_h = src_h * 2dst_w = src_w * 2print(f"dst image h:{src_h}, w:{src_w}")theta = cv2.getRotationMatrix2D(center=(src_w // 2, src_h // 2), angle=-30, scale=2)# using opencv warpAffinewarp_img_bgr = cv2.warpAffine(src=img_bgr,M=theta,dsize=(dst_w, dst_h),flags=cv2.INTER_LINEAR,borderValue=(0, 0, 0))cv2.imwrite("warp_img.jpg", warp_img_bgr)# using pytorch grid_sampletorch_img_bgr = torch.as_tensor(img_bgr, dtype=torch.float32).unsqueeze(0).permute([0, 3, 1, 2]) # [N,C,H,W]torch_theta = cal_torch_theta(theta, src_h, src_w, dst_h, dst_w).unsqueeze(0) # [N, 2, 3]grid = F.affine_grid(torch_theta, size=[1, 3, dst_h, dst_w])torch_warp_img_bgr = F.grid_sample(torch_img_bgr, grid=grid, mode="bilinear", padding_mode="zeros")torch_warp_img_bgr = torch_warp_img_bgr.permute([0, 2, 3, 1]).squeeze(0) # [H, W, C]cv2.imwrite("torch_warp_img.jpg", torch_warp_img_bgr.numpy())# save concat imgcv2.imwrite("compare_warp_img.jpg",np.concatenate([warp_img_bgr, torch_warp_img_bgr.numpy()], axis=1))if __name__ == '__main__':main()下图是生成的compare_warp_img.jpg图片,左边是通过Opencv warpAffine得到的图片,右边是通过Pytorch grid_sample得到的图片。可以看到基本是一致,如果使用专业的图像对比工具还是能看到像素差异(很难完全对齐)。

相关文章:

使用Pytoch实现Opencv warpAffine方法
随着深度学习的不断发展,GPU/NPU的算力也越来越强,对于一些传统CV计算也希望能够直接在GPU/NPU上进行,例如Opencv的warpAffine方法。Opencv的warpAffine的功能主要是做仿射变换,如果不了解仿射变换的请自行了解。由于Pytorch的图像…...
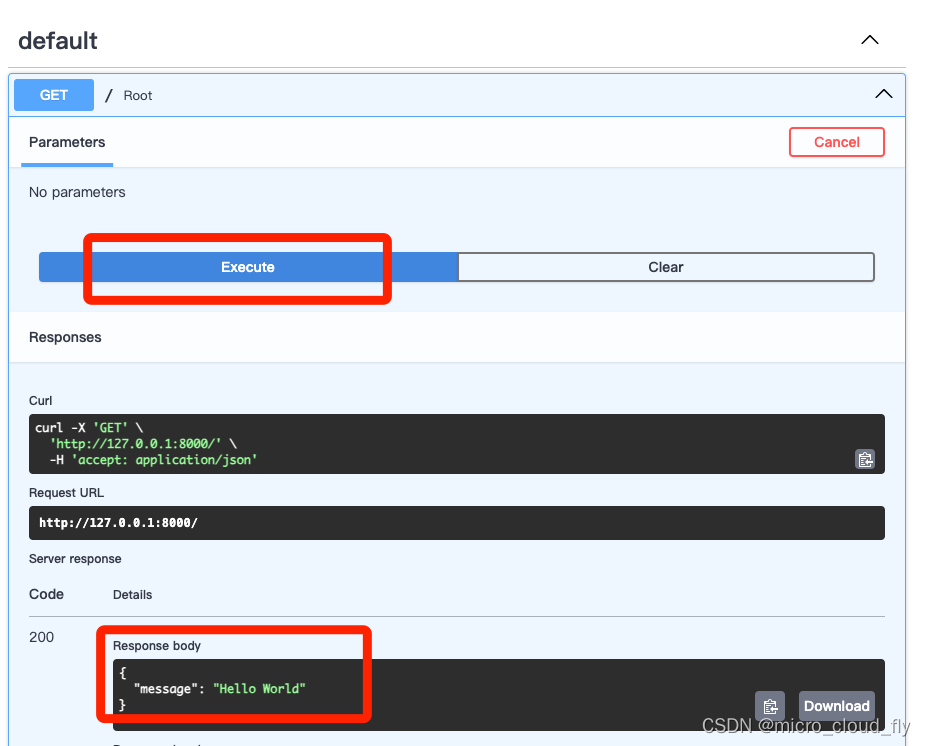
Hello World
世界上最著名的程序 from fastapi import FastAPIapp FastAPI()app.get("/") async def root():return {"message": "Hello World"}app.get("/hello/{name}") async def say_hello(name: str):return {"message": f"…...
【Python】Python读Excel文件生成xml文件
目录 前言 正文 1.Python基础学习 2.Python读取Excel表格 2.1安装xlrd模块 2.2使用介绍 2.2.1常用单元格中的数据类型 2.2.2 导入模块 2.2.3打开Excel文件读取数据 2.2.4常用函数 2.2.5代码测试 2.2.6 Python操作Excel官方网址 3.Python创建xml文件 3.1 xml语法…...
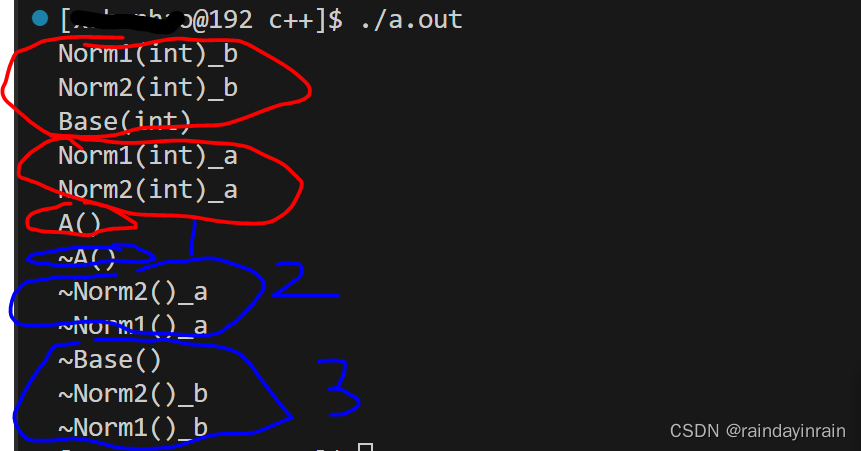
c++--类型行为控制
1.c的类 1.1.c的类关键点 c类型的关键点在于类存在继承。在此基础上,类存在构造,赋值,析构三类通用的关键行为。 类型提供了构造函数,赋值运算符,析构函数来让我们控制三类通用行为的具体表现。 为了清楚的说明类的构…...

笔记64:Bahdanau 注意力
本地笔记地址:D:\work_file\(4)DeepLearning_Learning\03_个人笔记\3.循环神经网络\第10章:动手学深度学习~注意力机制 a a a a a a a a a a a...

面试官问:如何手动触发垃圾回收?幸好昨天复习到了
在Java中,手动触发垃圾回收可以使用 System.gc() 方法。但需要注意,调用 System.gc() 并不能确保立即执行垃圾回收,因为具体的垃圾回收行为是由Java虚拟机决定的,而不受程序员直接控制。 public class GarbageCollectionExample …...
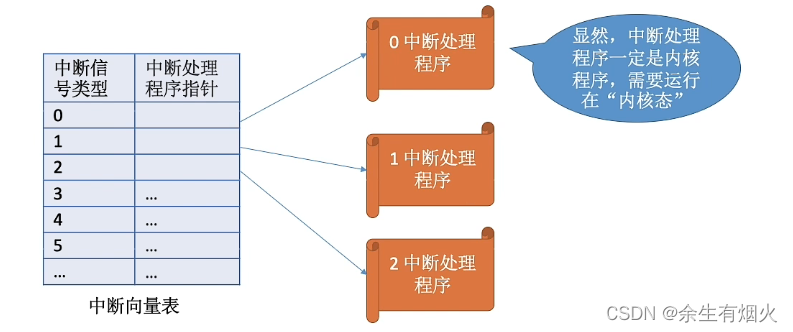
操作系统的运行机制+中断和异常
一、CPU状态 在CPU设计和生产的时候就划分了特权指令和非特叔指令,因此CPU执行一条指令前就能断出其类型 CPU有两种状态,“内核态”和“用户态” 处于内核态时,说明此时正在运行的是内核程序,此时可以执行特权指令。 处于用户态…...

Python实战:批量加密Excel文件指南
更多Python学习内容:ipengtao.com 大家好,我是彭涛,今天为大家分享 Python实战:批量加密Excel文件指南,全文3800字,阅读大约10分钟。 在日常工作中,保护敏感数据是至关重要的。本文将引导你通过…...
二叉树链式结构的实现和二叉树的遍历以及判断完全二叉树
二叉树的实现 定义结构体 我们首先定义一个结构来存放二叉树的节点 结构体里分别存放左子节点和右子节点以及节点存放的数据 typedef int BTDataType; typedef struct BinaryTreeNode {BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right; }BTNode;…...

vue中的动画组件使用及如何在vue中使用animate.css
“< Transition >” 是一个内置组件,这意味着它在任意别的组件中都可以被使用,无需注册。它可以将进入和离开动画应用到通过默认插槽传递给它的元素或组件上。进入或离开可以由以下的条件之一触发: 由 v-if 所触发的切换由 v-show 所触…...

qt 5.15.2 网络文件下载功能
qt 5.15.2 网络文件下载功能 #include <QCoreApplication>#include <iostream> #include <QFile> #include <QTextStream> // #include <QtCore> #include <QtNetwork> #include <QNetworkAccessManager> #include <QNetworkRep…...

Wifi adb 操作步骤
1.连接usb 到主机 手机开起热点,电脑和车机连接手机,或者电脑开热点,车机连接电脑,车机和电脑连接同一个网络 因为需要先使用usb,后面切换到wifi usb 2.查看车机ip地址,和电脑ip地址 电脑win键r 输入cmd…...

湿货 - 231206 - 关于如何构造输入输出数据并读写至文件中
TAG - 造数据、读写文件 造数据、读写文件 造数据、读写文件//*.in // #include<bits/stdc.h> using namespace std;/* *********** *********** 全局 ********** *********** */ string Pre_File_Name; ofstream IN_cout; int idx;void Modify_ABS_Path( string& …...
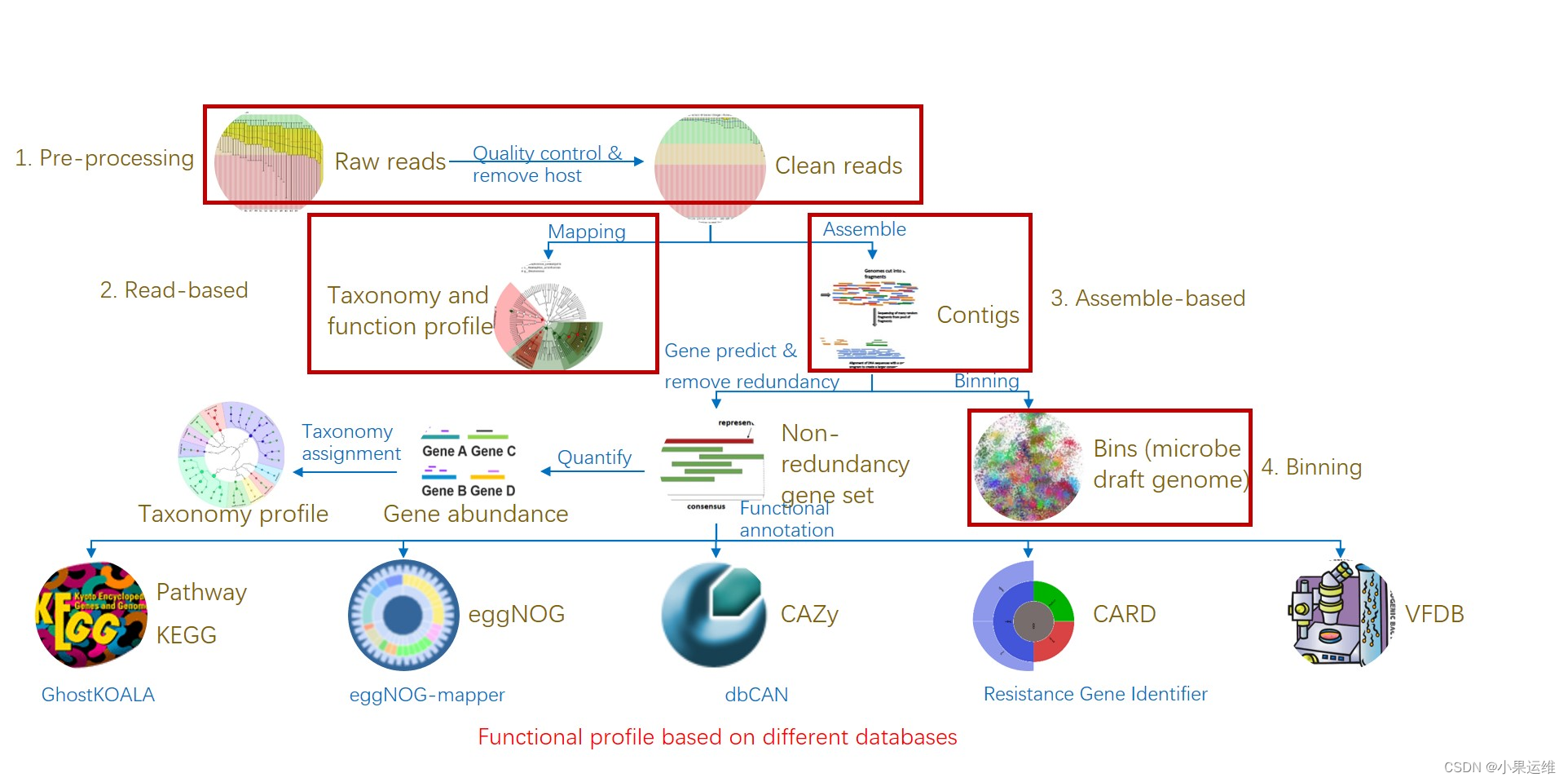
EasyMicrobiome-易扩增子、易宏基因组等分析流程依赖常用软件、脚本文件和数据库注释文件
啥也不说了,这个好用,给大家推荐:YongxinLiu/EasyMicrobiome (github.com) 大家先看看引用文献吧,很有用:https://doi.org/10.1002/imt2.83 还有这个,后面马上介绍:YongxinLiu/EasyAmplicon: E…...

【Python百宝箱】漫游Python数据可视化宇宙:pyspark、dash、streamlit、matplotlib、seaborn全景式导览
Python数据可视化大比拼:从大数据处理到交互式Web应用 前言 在当今数字时代,数据可视化是解释和传达信息的不可或缺的工具之一。本文将深入探讨Python中流行的数据可视化库,从大数据处理到交互式Web应用,为读者提供全面的了解和…...

企业数字档案馆室建设指南
数字化时代,企业数字化转型已经成为当下各行业发展的必然趋势。企业数字化转型不仅仅是IT系统的升级,也包括企业内部各种文件、档案、合同等信息的数字化管理。因此,建设数字档案馆室也变得尤为重要。本篇文章将为您介绍企业数字档案馆室建设…...

JavaScript中处理时间差
ES6版本 function countdown(endTime, includeSeconds true) {// 获取当前时间let now new Date();// 将传入的结束时间字符串转换为日期对象let endDateTime new Date(endTime);// 检查传入的时间字符串是否只包含日期(不包含时分秒)if (endTime.tr…...
Multidimensional Scaling(MDS多维缩放)算法及其应用
在这篇博客中,我将与大家分享在流形分析领域的一个非常重要的方法,即多维缩放MDS。整体来说,该方法提供了一种将内蕴距离映射到显性欧氏空间的计算,为非刚性形状分析提供了一种解决方案。当初就是因为读了Bronstein的相关工作【1】…...

单片机_RTOS_架构
一. RTOS的概念 // 经典单片机程序 void main() {while (1){喂一口饭();回一个信息();} } ------------------------------------------------------ // RTOS程序 喂饭() {while (1){喂一口饭();} }回信息() {while (1){回一个信息();} }void main() {create_task(喂饭);cr…...

Golang rsa 验证
一下代码用于rsa 签名的验签, 签名可以用其他语言产生。也可以用golang生成。 package mainimport ("crypto""crypto/rsa""crypto/sha256""crypto/x509""encoding/pem""errors""fmt" )fun…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...
