Java LeetCode篇-深入了解二叉树经典解法(三种方式实现:获取二叉树的最大深度)
🔥博客主页: 【小扳_-CSDN博客】
❤感谢大家点赞👍收藏⭐评论✍


文章目录
1.0 对称二叉树
1.1 判断对称二叉树实现思路
1.2 代码实现:判断对称二叉树
2.0 二叉树的最大深度
2.1 使用递归实现获取二叉树的最大深度思路
2.2 代码实现:使用递归实现获取二叉树的最大深度
2.3 使用非递归实现获取二叉树的最大深度思路
2.4 代码实现:使用非递归实现获取二叉树的最大深度
2.5 使用层序遍历实现获取二叉树的最大深度
2.6 代码实现:使用层序遍历实现获取二叉树的最大深度
3.0 二叉树的最小深度
3.1 使用递归实现获取二叉树的最小深度思路
3.2 代码实现:使用递归实现获取二叉树最小深度
3.3 使用层序遍历实现获取二叉树的最小深度思路
3.4 代码实现:使用层序遍历实现获取二叉树的最小深度
4.0 翻转二叉树
4.1 使用实现递归翻转二叉树思路
4.2 代码实现:使用递归翻转二叉树
5.0 二叉树经典解法的完整代码
1.0 对称二叉树
题目:
给你一个二叉树的根节点
root, 检查它是否轴对称。示例 1:
输入:root = [1,2,2,3,4,4,3] 输出:true示例 2:
输入:root = [1,2,2,null,3,null,3] 输出:falseOJ链接:
101. 对称二叉树
1.1 判断对称二叉树实现思路
假设该树的图:
具体思路为:如果当前节点的左子树的值等于当前节点的右子树时,可以说目前为止还是对称的,不能直接下结论,因为不能保证之后的节点是否对称。比如:当前节点的值为 1 ,它的左孩子的值为 2 ,它的右孩子的值为 2,此时可以说暂时是对称的,还需要接着向下判断。它的左孩子的左孩子的值为 3,它的右孩子的右孩子为 3 ,同理,现在还不能说明该树是否对称,当递归到底的时候,当前的节点的左右孩子都是 null ,此时可以返回 true ,不能足以证明该树对称,因为单单只是判断完外侧的节点,在外层回归的过程中,需要判断内层的节点是否对称,回归到节点值都为 2 的节点,接着进行内层递归,对于在外层判断完左孩子,那么接下来需要判断右孩子,同样,对于在外层判断完右孩子,那么接下来需要判断左孩子。如,刚刚的外层结束递出之后,开始回归,到节点为 2 的节点,对于左边的节点值为 2 的节点的右孩子,与右边的节点值为 2 的节点的左孩子进行比较,如果相同,由于说明不了什么,还得继续往下递出,直到该节点的左右孩子都为 null 时,可以返回 true 。最后返回到节点值为 1 的根节点中,可以得到该树是对称。
在无论是外层递出还是内层递出:
- 当左右孩子节点的值不相同的时候,就说明了该树时不相等的,直接返回 false ;
- 遇到一个节点的左孩子不为 null 而右孩子为 null 时,可以直接返回 false ,不需要接着往后递出了。同理,遇到一个节点的右孩子不为 null ,而左孩子为 null 时,直接返回 false ;
- 当且仅当,当该节点的左右孩子都为 null 时,返回 true ;
1.2 代码实现:判断对称二叉树
//判断对称二叉树public boolean isSymmetry(TreeNode root) {return isSymmetryRecursion(root.left,root.right);}private boolean isSymmetryRecursion(TreeNode left,TreeNode right) {if (left == null && right == null ) {return true;}if (left == null || right == null) {return false;}if (left.val != right.val) {return false;}return isSymmetryRecursion(left.left,right.right) && isSymmetryRecursion(left.right,right.left);}大体上的思路跟后序遍历二叉树一致。
2.0 二叉树的最大深度
题目:
给定一个二叉树
root,返回其最大深度。二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
示例 1:
输入:root = [3,9,20,null,null,15,7] 输出:3OJ链接:
104. 二叉树的最大深度
2.1 使用递归实现获取二叉树的最大深度思路
具体思路为:先从整体思路出发,得到最大的深度,无非就是比较左右子树的深度,选取较大的值 + 1,返回即可。当遇到的节点为 null 时,返回 0 ,结束递出。比如,节点值为 3 的节点,它的左子树的深度为 1,它的右子树的深度为 2 ,那么选取最大的值为 2 ,最后最大的值再加上 1 ,所以得出的该树的最大深度为 3 。
接下来具体分析每一个节点:根节点值为 3 ,先获取左子树的深度:沿着该方向递出,直到遇到当前节点的左右孩子都为 null 时,返回 0 ,所以值为 9 的节点目前返回上一个递归调用的值为 1 ,对于根节点的左子树的深度为 1 ;再获取右子树的深度:沿着根节点的右子树递出,这次遇到的节点的左右子树都不为 null 时,对于当前值为 20 的节点来说,需要获取该左右子树的最大的值,先获取左子树的深度:沿着该方式递出,直到遇到的节点为 null 时,返回 0,节点值为 15 的节点的左右孩子都为 null ,返回 0 + 1 ,所以对于节点 20 来说,该左子树的深度为 1 ;接着继续来获取节点值为 20 的右子树的深度:沿着该方式递出,直到遇到的节点为 null 时,返回 0,节点值为 7 的左右孩子都为 null ,返回 0 + 1。那么选取较大的值 + 1,就是节点值为 20 的深度为 2 。相对与根节点来说已经得到了左右子树的深度了,分别为 1 与 2 ,选取最大的值 2 再加 1 就是该树的最大深度为 3 。
2.2 代码实现:使用递归实现获取二叉树的最大深度
//用递归方式求树的最大深度public int maximumDepthRecursion(TreeNode node) {if (node == null) {return 0;}int l = maximumDepth(node.left);int r = maximumDepth(node.right);return Math.max(l,r) + 1;}大体上思路跟后序遍历思路大致相同。
2.3 使用非递归实现获取二叉树的最大深度思路
具体思路为:在之前讲到使用非递归实现后序遍历的思路,跟这里的思路大致一致。简单再讲一下思路,根节点从左孩子开始出发,在到下一个节点之前,需要先把该节点压入栈中,直到 node == null 时,不再继续下去,按照原路返回。由于需要完成对右节点的操作后,需要返回该节点,所以不能直接把栈顶元素弹出,先查找栈顶元素,查看该右孩子是否为 null 或者已经完成对右孩子的相关操作之后,这才能弹出栈顶元素。如果以上情况都不符合,需要对右孩子进行处理。以上就是使用非递归实现后序循环,那么结合该题求树的最大深度,即什么时候栈的元素达到最大的时候,这时候就是树的最大深度。
2.4 代码实现:使用非递归实现获取二叉树的最大深度
//用非递归方式求树的最大深度public int maximumDepth(TreeNode root) {TreeNode curr = root;LinkedList<TreeNode> stack = new LinkedList<>();int max = 0;TreeNode pop = null;while (curr != null || !stack.isEmpty()) {if (curr != null) {stack.push(curr);curr = curr.left;if (max < stack.size()) {max = stack.size();}} else {TreeNode peek = stack.peek();if ( peek.right == null || peek.right == pop ) {pop = stack.pop();}else {curr = peek.right;}}}return max;}当然,这个时间复杂度比使用递归实现的要大,效率不如使用递归的实现二叉树最大深度。
2.5 使用层序遍历实现获取二叉树的最大深度
先了解层序遍历:顾名思义,按照层级进行依次访问节点。将每个节点压入队列中,按照先进先出的顺序依次访问队列中的节点。具体来说,我们从根节点开始,将根节点压入队列中,然后依次从队列中取出节点,将其左右子节点(如果存在)压入队列中。
需要准备队列来存储节点,根据该数据结构的特性:先进先出,一开始先让根节点压入队列中,接着从队列中弹出来,如果弹出来的节点的左孩子不为 null 时,将其压入队列中;如果左孩子为 null 时,不需要压入队列中;同理,如果弹出来节点的右孩子不为 null 时,将其压入队列中。循环结束条件为:当队列中的元素个数为 0 时,退出循环。
再结合该题的逻辑,该二叉树的最大深度就是树的层级数量。那么怎么才能得出 int depth 层级数量呢?再嵌套一个内层循环,每一层遍历结束之后,depth++ 。内层循环的次数为:当前的队列的元素的个数。
2.6 代码实现:使用层序遍历实现获取二叉树的最大深度
//使用层序遍历求树的最大深度public int sequenceMaxDepth(TreeNode root) {if (root == null) {return 0;}LinkedList<TreeNode> queue = new LinkedList<>();queue.offer(root);int depth = 0;while ( !queue.isEmpty()) {int size = queue.size();for (int j = 0; j < size; j++) {TreeNode tp = queue.poll();if (tp.left != null) {queue.offer(tp.left);}if (tp.right != null) {queue.offer(tp.right);}//System.out.print(tp.val + " ");}//System.out.println();depth++;}return depth;}
3.0 二叉树的最小深度
题目:
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:
输入:root = [3,9,20,null,null,15,7] 输出:2OJ链接:
111. 二叉树的最小深度
二叉树的最小深度是指从根节点到最近叶子节点的最短路径上的节点数量。换句话说,最小深度是从根节点到最近的叶子节点的路径长度。
3.1 使用递归实现获取二叉树的最小深度思路
具体思路为:思路大体跟或去最大深度的思路差不太多,当比较前节点的左右子树,获取最小的值 + 1 ,则为当前节点的深度。获取最小深度相较于获取最大深度,多了一个判断条件,如果当前节点为 0 时,不应该参与比较。
如图例,该树的深度应该为 2 ,如果不加额外的条件来判断左右孩子节点是否为 null 时,那么此时根节点的右孩子为 null ,所以右子树为深度为 0 ;左孩子不为 null ,接着递归下去,直到 node == null 为止,从图可知,该根节点的左子树的深度为 1,因此用 1 与 0 来比较,获取最小的值为 0 ,再加上 1 ,最后结果为 1 。很明显不符合要求。所以,一定要加条件来判断,查看该节点的左右孩子是否为 null ,如果为 null ,需要返回另一个节点 + 1 当作当前节点的深度。
3.2 代码实现:使用递归实现获取二叉树最小深度
//使用递归求树的最小深度public int minDepth(TreeNode node) {if (node == null) {return 0;}int l = minDepth(node.left);int r = minDepth(node.right);if (l == 0) {return r + 1;}if (r == 0) {return l + 1;}return Math.min(l,r) + 1;}
3.3 使用层序遍历实现获取二叉树的最小深度思路
具体思路为:当带一个遇到的叶子节点时,当前的层数就是该树的最小深度。
3.4 代码实现:使用层序遍历实现获取二叉树的最小深度
//使用层序遍历求得树的最小深度public int sequenceMinDepth(TreeNode root) {LinkedList<TreeNode> queue = new LinkedList<>();queue.offer(root);int depth = 0;while (!queue.isEmpty()) {depth++;int size = queue.size();for (int i = 0; i < size ; i++) {TreeNode poll = queue.poll();if (poll.right == null && poll.left == null) {return depth;}if (poll.left != null) {queue.offer(poll.left);}if (poll.right != null) {queue.offer(poll.right);}}}return depth;}
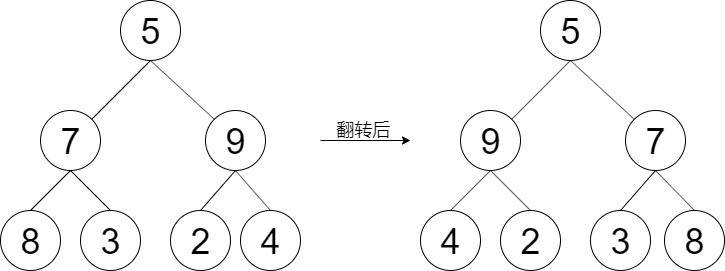
4.0 翻转二叉树
题目:
给定一棵二叉树的根节点
root,请左右翻转这棵二叉树,并返回其根节点。示例 1:
输入:root = [5,7,9,8,3,2,4] 输出:[5,9,7,4,2,3,8]OJ链接:
LCR 144. 翻转二叉树
4.1 使用实现递归翻转二叉树思路
具体思路为:从整体来看,将当前节点的左右节点进行翻转,每一个节点都是如此,递归结束条件为 node == null 时,结束递出。回归到每一个节点的右子树进行翻转。
4.2 代码实现:使用递归翻转二叉树
//翻转二叉树public void rollbackRecursion(TreeNode node) {if (node == null) {return;}TreeNode temp = node.left;node.left = node.right;node.right = temp;rollbackRecursion(node.left);rollbackRecursion(node.right);}
5.0 二叉树经典解法的完整代码
回顾本章代码,进一步巩固:
import java.util.ArrayList; import java.util.LinkedList; import java.util.List;public class TreeNode {private TreeNode left;private int val;private TreeNode right;public TreeNode(int val) {this.val = val;}public TreeNode(TreeNode left, int val, TreeNode right) {this.left = left;this.val = val;this.right = right;}//递归实现前序遍历public void prevRecursion(TreeNode node) {if (node == null) {return;}System.out.print(node.val + " ");prevRecursion(node.left);prevRecursion(node.right);}//递归实现中序遍历public void midRecursion(TreeNode node) {if (node == null) {return;}midRecursion(node.left);System.out.print(node.val + " ");midRecursion(node.right);}//递归实现后序遍历public void postRecursion(TreeNode node) {if (node == null) {return;}postRecursion(node.left);postRecursion(node.right);System.out.print(node.val + " ");}//非递归实现前序遍历public List<Integer> prev(TreeNode root) {TreeNode node = root;LinkedList<TreeNode> stack = new LinkedList<>();List<Integer> list = new ArrayList<>();while (node != null || !stack.isEmpty()) {if (node != null) {stack.push(node);list.add(node.val);node = node.left;}else {TreeNode tp = stack.pop();node = tp.right;}}return list;}//非递归实现中序遍历public void mid(TreeNode root) {TreeNode node = root;LinkedList<TreeNode> stack = new LinkedList<>();while (node != null || !stack.isEmpty()) {if (node != null) {stack.push(node);node = node.left;}else {TreeNode tp = stack.pop();System.out.print(tp.val + " ");node = tp.right;}}System.out.println();}//非递归实现后序遍历public List<Integer> post(TreeNode root) {TreeNode node = root;TreeNode pop = null;List<Integer> list = new ArrayList<>();LinkedList<TreeNode> stack = new LinkedList<>();while ( node != null || !stack.isEmpty()) {if (node != null) {stack.push(node);node = node.left;}else {TreeNode tp = stack.peek();if (tp.right == null || tp.right == pop) {pop = stack.pop();list.add(pop.val);}else {node = tp.right;}}}return list;}//判断对称二叉树public boolean isSymmetry(TreeNode root) {return isSymmetryRecursion(root.left,root.right);}private boolean isSymmetryRecursion(TreeNode left,TreeNode right) {if (left == null && right == null ) {return true;}if (left == null || right == null) {return false;}if (left.val != right.val) {return false;}return isSymmetryRecursion(left.left,right.right) && isSymmetryRecursion(left.right,right.left);}//用递归方式求树的最大深度public int maximumDepthRecursion(TreeNode node) {if (node == null) {return 0;}int l = maximumDepth(node.left);int r = maximumDepth(node.right);return Math.max(l,r) + 1;}//用非递归方式求树的最大深度public int maximumDepth(TreeNode root) {TreeNode curr = root;LinkedList<TreeNode> stack = new LinkedList<>();int max = 0;TreeNode pop = null;while (curr != null || !stack.isEmpty()) {if (curr != null) {stack.push(curr);curr = curr.left;if (max < stack.size()) {max = stack.size();}} else {TreeNode peek = stack.peek();if ( peek.right == null || peek.right == pop ) {pop = stack.pop();}else {curr = peek.right;}}}return max;}//使用层序遍历求树的最大深度public int sequenceMaxDepth(TreeNode root) {if (root == null) {return 0;}LinkedList<TreeNode> queue = new LinkedList<>();queue.offer(root);int depth = 0;while ( !queue.isEmpty()) {int size = queue.size();for (int j = 0; j < size; j++) {TreeNode tp = queue.poll();if (tp.left != null) {queue.offer(tp.left);}if (tp.right != null) {queue.offer(tp.right);}//System.out.print(tp.val + " ");}//System.out.println();depth++;}return depth;}//使用递归求树的最小深度public int minDepth(TreeNode node) {if (node == null) {return 0;}int l = minDepth(node.left);int r = minDepth(node.right);if (l == 0) {return r + 1;}if (r == 0) {return l + 1;}return Math.min(l,r) + 1;}//使用层序遍历求得树的最小深度public int sequenceMinDepth(TreeNode root) {LinkedList<TreeNode> queue = new LinkedList<>();queue.offer(root);int depth = 0;while (!queue.isEmpty()) {depth++;int size = queue.size();for (int i = 0; i < size ; i++) {TreeNode poll = queue.poll();if (poll.right == null && poll.left == null) {return depth;}if (poll.left != null) {queue.offer(poll.left);}if (poll.right != null) {queue.offer(poll.right);}}}return depth;}//翻转二叉树public void rollbackRecursion(TreeNode node) {if (node == null) {return;}TreeNode temp = node.left;node.left = node.right;node.right = temp;rollbackRecursion(node.left);rollbackRecursion(node.right);}}
相关文章:
Java LeetCode篇-深入了解二叉树经典解法(三种方式实现:获取二叉树的最大深度)
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 对称二叉树 1.1 判断对称二叉树实现思路 1.2 代码实现:判断对称二叉树 2.0 二叉树的最大深度 2.1 使用递归实现获取二叉树的最大深度思路 2.2 代码实…...
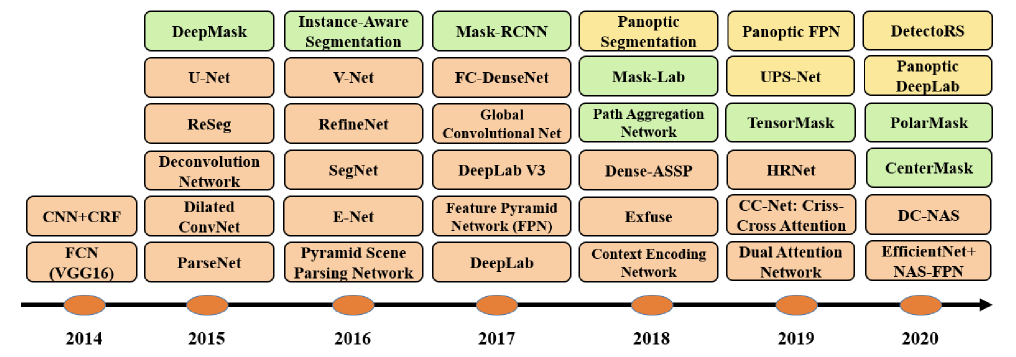
Image Segmentation Using Deep Learning: A Survey
论文标题:Image Segmentation Using Deep Learning:A Survey作者:发表日期:阅读日期 :研究背景:scene understanding,medical image analysis, robotic perception, video surveillance, augmented reality, and image…...
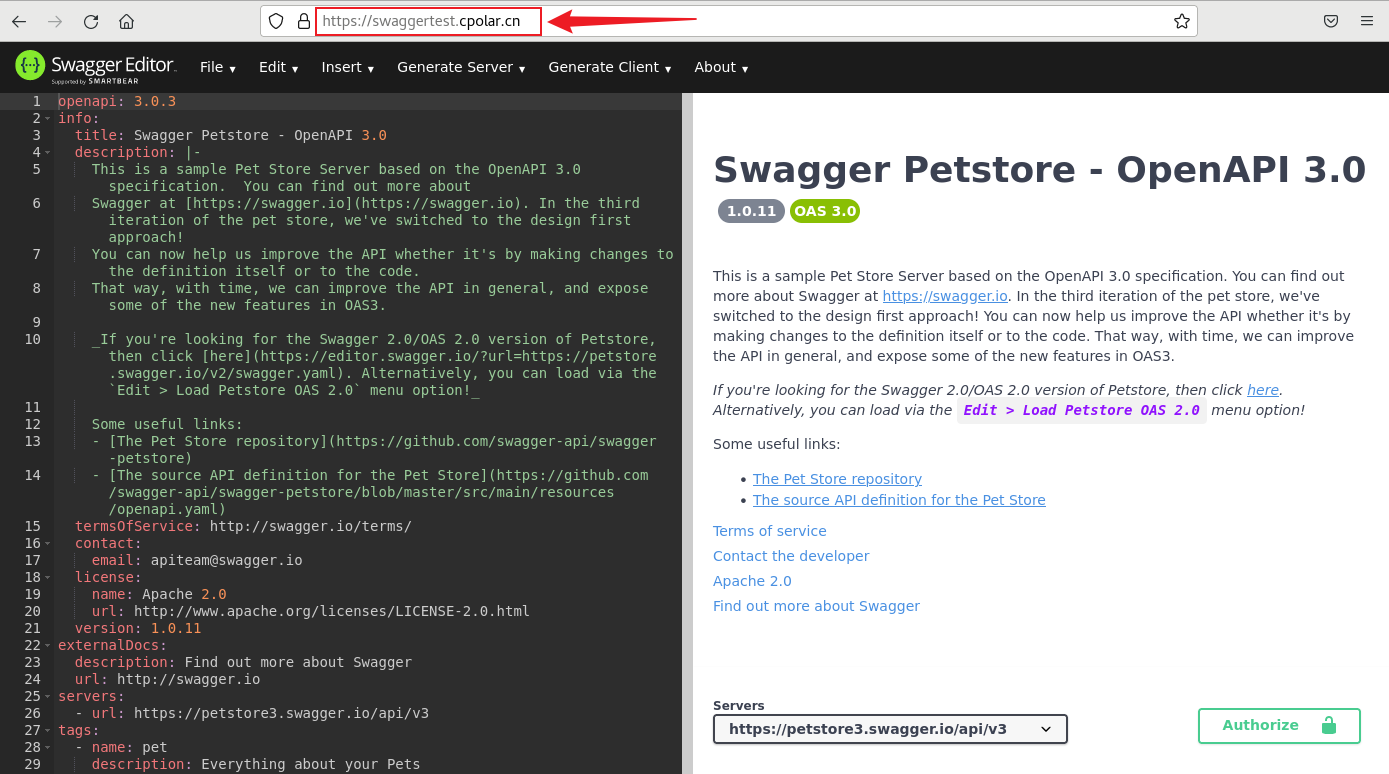
可视化开源编辑器Swagger Editor本地部署并实现远程访问管理编辑文档
最近,我发现了一个超级强大的人工智能学习网站。它以通俗易懂的方式呈现复杂的概念,而且内容风趣幽默。我觉得它对大家可能会有所帮助,所以我在此分享。点击这里跳转到网站。 文章目录 Swagger Editor本地接口文档公网远程访问1. 部署Swagge…...
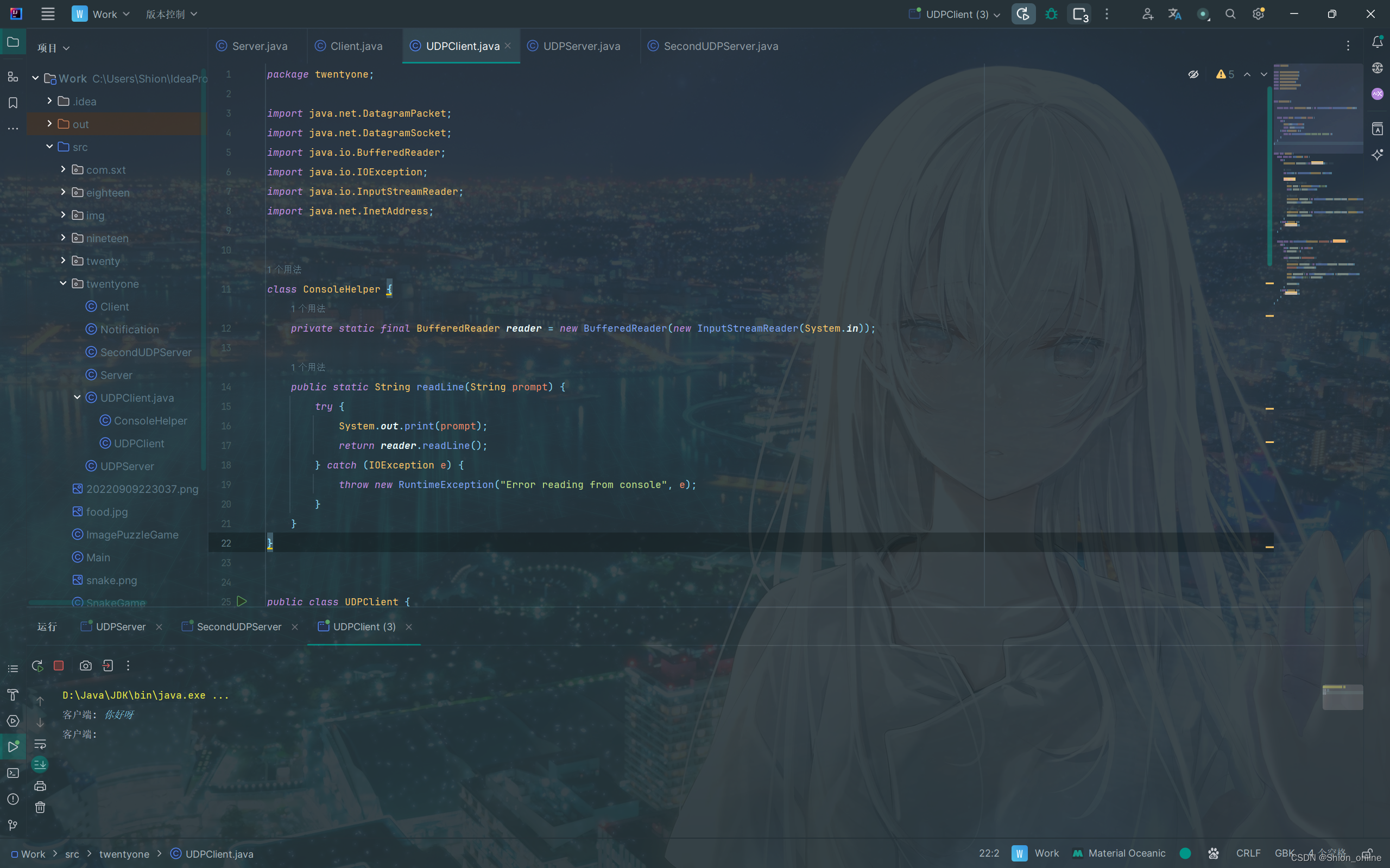
Java TCP协议实现一对一聊天与UDP协议实现群聊案例
JavaTCP协议实现一对一聊天与UDP协议实现群聊案例 1.TCP协议实现一对一聊天 1.1服务端运行结果 1.2客服端运行结果 1.3代码汇总 服务端 package twentyone;import java.io.IOException; import java.io.BufferedReader; import java.io.InputStreamReader; import java.io.…...
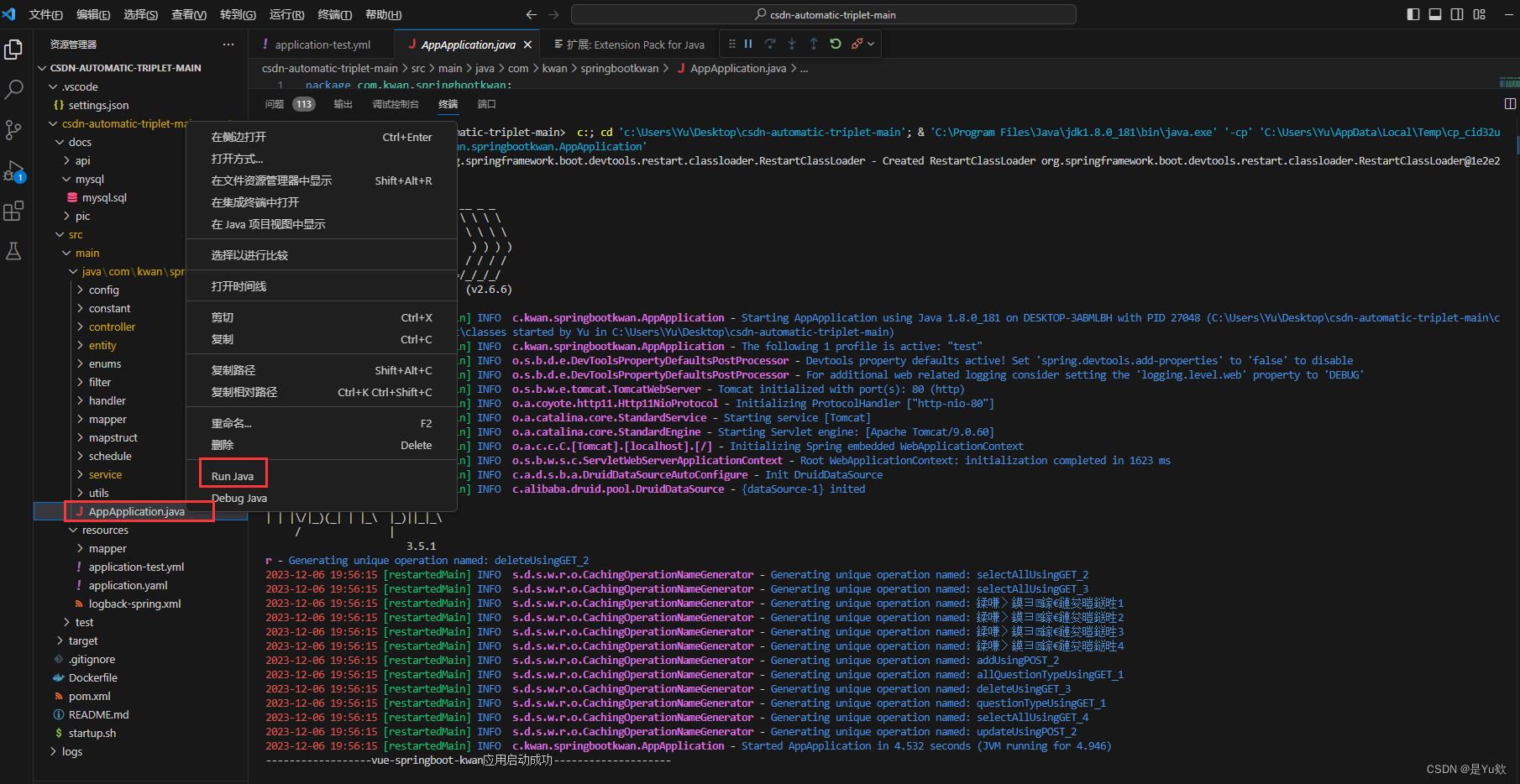
【从0配置JAVA项目相关环境1】jdk + VSCode运行java + mysql + Navicat + 数据库本地化 + 启动java项目
从0配置JAVA项目相关环境 写在最前面一、安装Java的jdk环境1. 下载jdk2. 配置jdk3. 配置环境变量 二、在vscode中配置java运行环境1. 下载VSCode2. 下载并运行「Java Extension Pack」 三、安装mysql1.官网下载MySQL2.开始安装如果没有跳过安装成功 3.配置MySQL Server4.环境变…...

人工智能_机器学习053_支持向量机SVM目标函数推导_SVM条件_公式推导过程---人工智能工作笔记0093
然后我们再来看一下支持向量机SVM的公式推导情况 来看一下支持向量机是如何把现实问题转换成数学问题的. 首先我们来看这里的方程比如说,中间的黑线我们叫做l2 那么上边界线我们叫l1 下边界线叫做l3 如果我们假设l2的方程是上面这个方程WT.x+b = 0 那么这里 我们只要确定w和…...

二叉树的前、中和后序遍历的递归与迭代实现
1. 前序遍历 1.1 递归 /*** Definition for a binary tree node.* function TreeNode(val, left, right) {* this.val (valundefined ? 0 : val)* this.left (leftundefined ? null : left)* this.right (rightundefined ? null : right)* }*/ /*** param …...

人体姿态估计算法
人体姿态估计算法 1 什么是人体姿态估计2 基于经典传统和基于深度学习的方法2.1 基于经典传统的人体姿态估计算法2.2 基于深度学习的人体姿态估计算法OpenPoseAlphaPose (RMPE) 3 算法应用4 Paper 人体姿态估计在现实中的应用场景很丰富,如下 动作捕捉:三…...
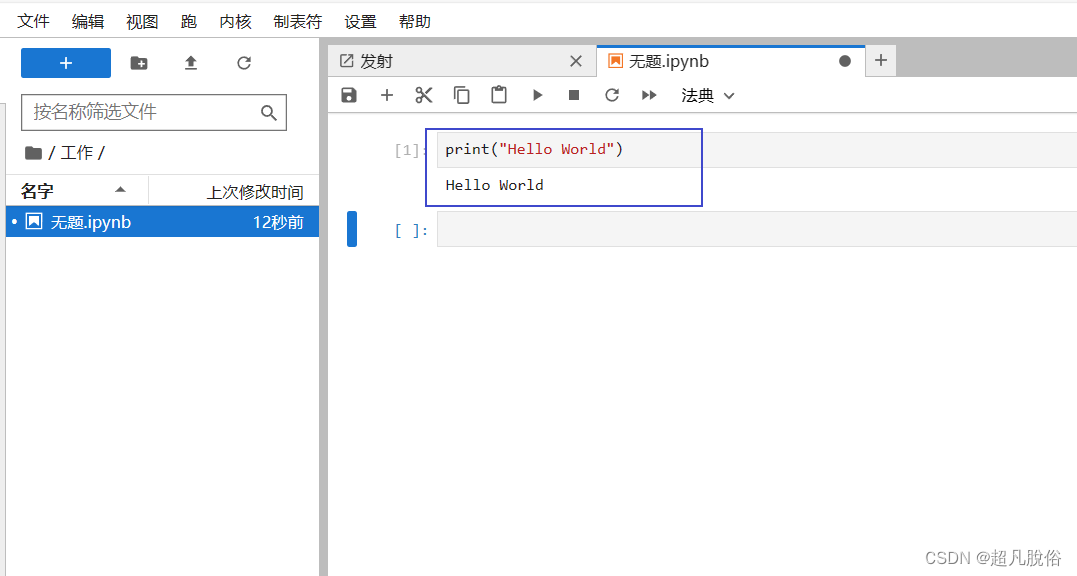
docker部署jupyter
文章目录 1.搜索镜像2.拉取镜像3.创建挂载4.运行容器4.查看容器运行运行状态5.token查看6.访问jupyter 1.搜索镜像 docker search jupyter: 命令用于在 Docker Hub 上搜索名为 “jupyter” 的镜像。搜索结果显示了一个名为 “jupyter/datascience-notebook” 的镜像࿰…...
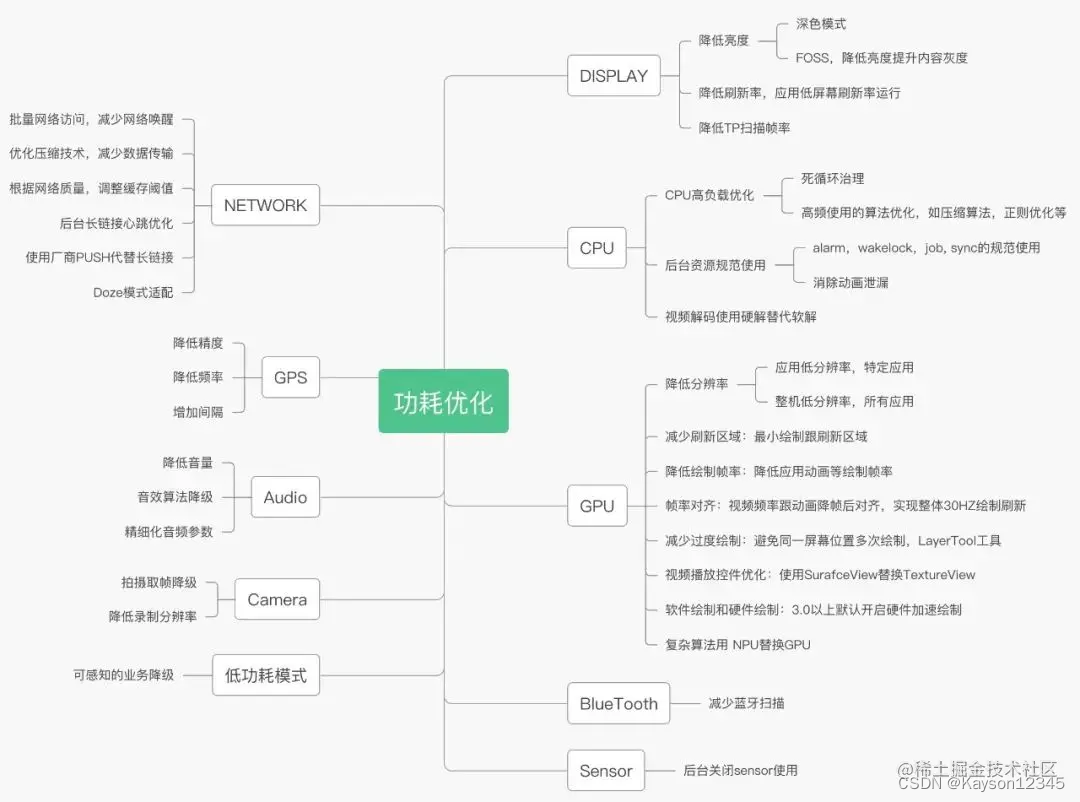
音视频的功耗优化
前言 在应用中,录制与音视频模块往往是高耗能的模块,设备容易发热,影响体验。 什么是功耗优化 手机有多个耗电模块, SOC(CPU,GPU,DDR),Display,Audio,Video࿰…...

Python实现FA萤火虫优化算法优化XGBoost回归模型(XGBRegressor算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 萤火虫算法(Fire-fly algorithm,FA)由剑桥大学Yang于2009年提出 , …...

SCAUoj综合性实验
Last One ! 文章目录 1109 综合实验:文件操作与字符处理总结 1109 综合实验:文件操作与字符处理 时间限制:4000MS 代码长度限制:10KB 提交次数:6265 通过次数:1646 题型: 填空题 语言: GCC Description 在当前目录中存在文件名为"case1.in"&…...

智加科技获全国首张重卡无人驾驶开放道路测试牌照
2023年12月1日,智加科技获得苏州市智能网联汽车无人化测试牌照。该牌照也是江苏省及国内首张无人重卡开放高速公路全路段全场景全息路网(S17苏台高速)道路测试牌照。 该重卡无人驾驶开放道路测试牌照,经由苏州市智能网联汽车联席小…...

LLM大语言模型(一):ChatGLM3-6B本地部署
目录 前言 本机环境 ChatGLM3代码库下载 模型文件下载 修改为从本地模型文件启动 启动模型网页版对话demo 超参数设置 GPU资源使用情况 (网页对话非常流畅) 前言 LLM大语言模型工程化,在本地搭建一套开源的LLM,方便后续的…...

chatgpt prompt提示词
chatgpt的接口是一个标准的http请求,请求的url为 POST https://api.openai.com/v1/chat/completions 官方的接口文档地址为:https://platform.openai.com/docs/api-reference/chat/create Example request curl https://api.openai.com/v1/chat/comp…...

【PyTorch】数据集
文章目录 1. 创建数据集1.1. 直接继承Dataset类1.2. 使用TensorDataset类 2. 数据集的划分3. 加载数据集4. 将数据转移到GPU 1. 创建数据集 主要是将数据集读入内存,并用Dataset类封装。 1.1. 直接继承Dataset类 必须要重写__getitem__方法,用于根据索…...
)
oops-framework框架 之 本地存储(五)
引擎: CocosCreator 3.8.0 环境: Mac Gitee: oops-game-kit 注: 作者dgflash的oops-framework框架QQ群: 628575875 简介 在CocosCreator中,本地存储主要使用sys.localStorage 接口,通过 key-value的格式进…...

编程常见的问题
在现代社会中,编程已经成为一项非常重要的技能。随着科技的不断发展和普及,计算机已经渗透到我们生活的方方面面,从个人电脑、手机到智能家居、自动驾驶等。编程作为计算机科学的基础,为我们提供了解决问题和创造新事物的工具和方…...

针对Arrays.asList的坑,可以有哪些处理措施
上文讲述:Error querying database. Cause: java.lang.reflect.InaccessibleObjectException: 那么如果真的只习惯用Arrays.asList,那也是有对应的解决办法的。 一、解决办法大方向 不管做什么事情,都是先判定一个大方向,不管是…...
SE考研真题总结(一)
本帖开始分享考研真题中设计【软件工程】的部分,预计会出5期左右,敬请期待~ 一.单选题 1.程序编写不是软件质量保障过程~ 静态代码扫描是今年来多数被人提及的软件应用安全解决方案之一,指程序员在编写好代码后无需进行编译,直接…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...