c语言:整数与浮点数在内存中的存储方式
整数在内存中的存储:
在计算机内存中,整数通常以二进制形式存储。计算机使用一定数量的比特(bit)来表示整数,比如32位或64位。在存储整数时,计算机使用补码形式来表示负数,而使用原码形式来表示正数。整数的存储方式使得计算机能够进行加减乘除等运算。
浮点数在内存中的存储:
与整数不同,浮点数采用IEEE 754标准来存储。在内存中,浮点数由三个部分组成:符号位、指数位和尾数位。这种存储方式使得计算机能够表示小数和非常大或非常小的数字,但也带来了精度丢失的问题。
IEEE 754标准
IEEE 754标准定义了浮点数的存储格式,包括单精度浮点数(32位)和双精度浮点数(64位)。在这两种格式中,浮点数的存储结构都由三个部分组成:符号位、指数位和尾数位。
-
符号位:用于表示浮点数的正负,0表示正数,1表示负数。
-
指数位:用于表示浮点数的阶码(指数部分),指数位的长度决定了浮点数的表示范围。
-
尾数位:用于表示浮点数的尾数,尾数位的长度决定了浮点数的精度。
单精度浮点数(32位)
单精度浮点数采用32位来存储,其中1位用于符号位,8位用于指数位,23位用于尾数位。
符号位(1位) 指数位(8位) 尾数位(23位)双精度浮点数(64位)
双精度浮点数采用64位来存储,其中1位用于符号位,11位用于指数位,52位用于尾数位。
符号位(1位) 指数位(11位) 尾数位(52位)
特别注意:
当我们使用单精度浮点数(32位)来存储一个小数时,可能会出现精度丢失的情况。例如,让我们考虑存储十进制数 0.1 在单精度浮点数中的表示。
在十进制中,0.1 可以用有限位数准确表示,但在二进制中,0.1 是一个无限循环小数。因此,在单精度浮点数中,0.1 的精确表示是不可能的。
让我们看看单精度浮点数中存储 0.1 的近似表示:
首先,将 0.1 转换为二进制。0.1 的二进制表示是 0.00011001100110011001100110...,这是一个无限循环。
然后,根据单精度浮点数的格式,我们将其表示为科学计数法形式:1.100110011001100110011002 x 2^-4。
在单精度浮点数中,我们需要舍入到23位尾数。因此,最终存储的近似值是:
符号位:0(正数)
指数位:-4 + 127(偏移值,127是单精度浮点数的偏移量)
尾数位:10011001100110011001100
这个存储的近似值会导致精度丢失,因为实际的0.1在单精度浮点数中无法被精确表示。在进行浮点数运算时,这种精度丢失可能会积累导致不准确的结果。
举个例子:
#include <stdio.h>
#include <stdint.h>int main()
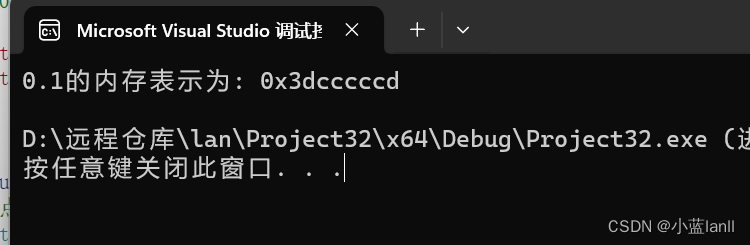
{float num = 0.1f; // 使用单精度浮点数表示0.1// 将浮点数的内存表示以十六进制打印出来uint32_t* ptr = (uint32_t*)#printf("0.1的内存表示为: 0x%08x\n", *ptr);return 0;
}
#include <stdio.h>
#include <stdint.h>int main()
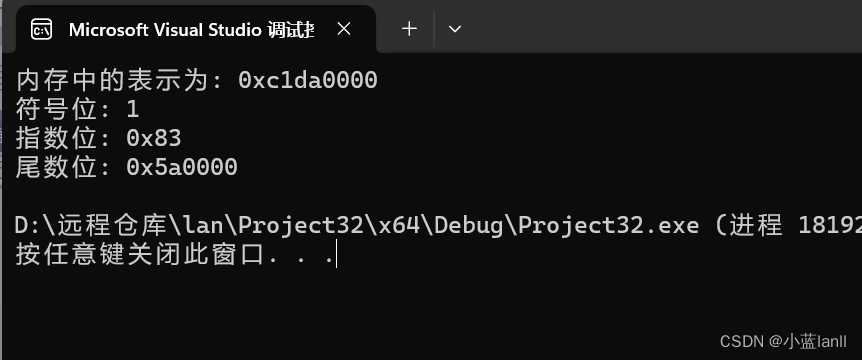
{float num = -27.25f; // 使用单精度浮点数表示-27.25// 将浮点数的内存表示以十六进制打印出来uint32_t* ptr = (uint32_t*)#printf("内存中的表示为: 0x%08x\n", *ptr);// 分别提取符号位、指数位和尾数位uint32_t sign = (*ptr >> 31) & 0x1;uint32_t exponent = (*ptr >> 23) & 0xFF;uint32_t mantissa = *ptr & 0x7FFFFF;printf("符号位: %d\n", sign);printf("指数位: 0x%x\n", exponent);printf("尾数位: 0x%x\n", mantissa);return 0;
}
符号位:1位
┌─────┬───────────────────────┬─────────────────────────────────────┐
| S | 指数位(E) | 尾数位(M) |
└─────┴───────────────────────┴─────────────────────────────────────┘31 23 0例如 1.5,
符号位:1位
┌─────┬───────────────────────┬─────────────────────────────────────┐
| 0 | 01111111 | 10000000000000000000000 |
└─────┴───────────────────────┴─────────────────────────────────────┘31 23 0- 符号位(S):用于表示浮点数的正负,0表示正数,1表示负数。
- 指数位(E):用于表示浮点数的指数部分,通过偏移(bias)来表示实际的指数值。
- 尾数位(M):用于表示浮点数的尾数部分,包括小数点后面的数字。
相关文章:

c语言:整数与浮点数在内存中的存储方式
整数在内存中的存储: 在计算机内存中,整数通常以二进制形式存储。计算机使用一定数量的比特(bit)来表示整数,比如32位或64位。在存储整数时,计算机使用补码形式来表示负数,而使用原码形式来表示…...

dockerdesktop 导出镜像,导入镜像
总体思路 备份时 容器 > 镜像 > 本地文件 恢复时 本地文件 > 镜像 > 容器 备份步骤 首先,把容器生成为镜像 docker commit [容器名称] [镜像名称] 示例 docker commit nginx mynginx然后,把镜像备份为本地文件,如果使用的是Docker Desktop,打包备份的文件会自动存…...

2-Django、Flask和Tornado三大主流框架对比
在Python的web开发框架中,目前使用量最高的几个是Django、Flask和Tornado, 经常会有人拿这几个对比,相信大家的初步印象应该是 Django大而全、Flask小而精、Tornado性能高。 了解常用框架 Django 主要特点是大而全,集成了很多组件,例如: Mo…...
【openssl】Window系统如何编译openssl
本文主要记录如何编译出windows版本的openss的lib库 如果需要获取RSA公钥私钥,推荐【openssl】 生成公钥私钥 |通过私钥获取公钥-CSDN博客 目录 1.下载openssl,获得openssl-master.zip。 2.下载Perl 3.下载NASM 4.配置perl和NASM的环境变量 5.进入…...

[leetcode 双指针]
1. 三数之和 M :::details 给你一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a b c 0 ?请你找出所有和为 0 且不重复的三元组。 注意:答案中不可以包含重复的三元组。 示例…...
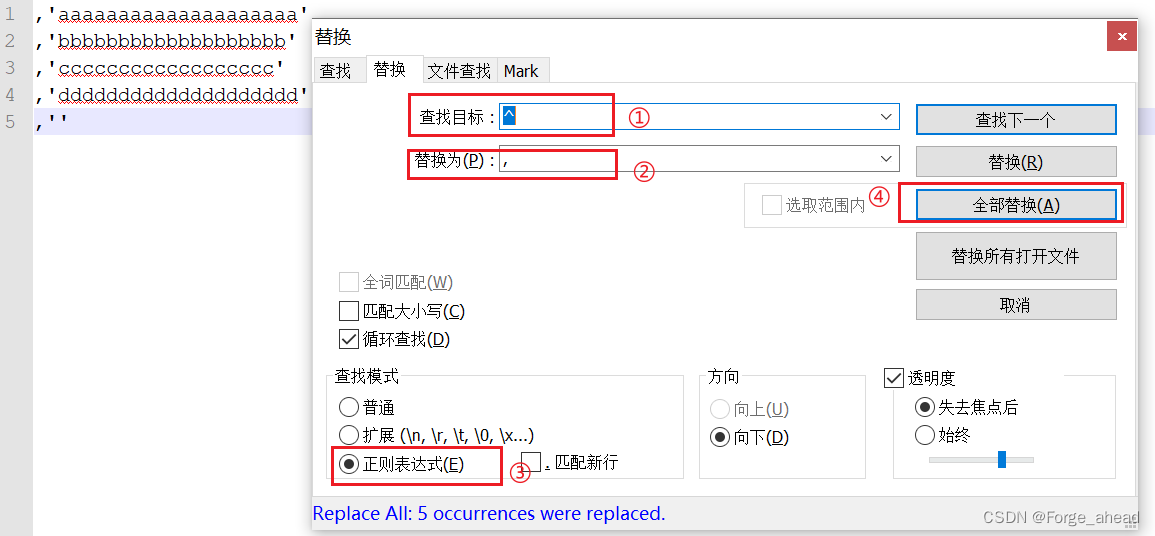
Notepad++批量添加引号
工作中经常会遇到这样情景:业务给到一批订单号,需要查询这批订单的某些字段信息。在where条件中需要传入这些订单号的数组,并且订单号用引号引起,用引号隔开。 字符串之间长度相同 可以按住CtrlAlt和鼠标左键选中区域࿰…...
HarmonyOS4.0从零开始的开发教程04 初识ArkTS开发语言(下)
HarmonyOS(二) 初识ArkTS开发语言(下)之TypeScript入门 声明式UI基本概念 应用界面是由一个个页面组成,ArkTS是由ArkUI框架提供,用于以声明式开发范式开发界面的语言。 声明式UI构建页面的过程ÿ…...
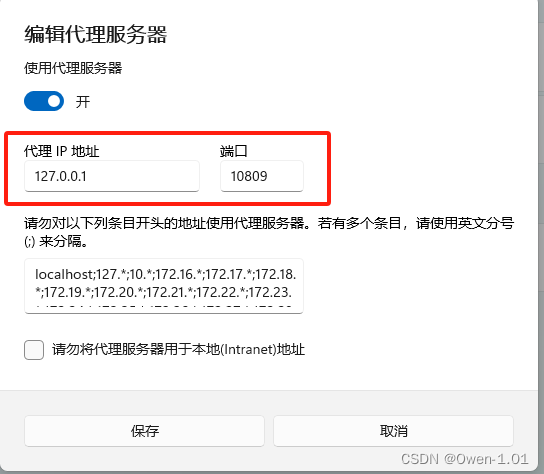
Failed to connect to github.com port 443 after 21055 ms: Timed out
目前自己使用了梯*子还是会报这样的错误,连接不到的github。 查了一下原因: 是因为这个请求没有走代理。 解决方案: 设置 -> 网络和Internet -> 代理 -> 编辑 记住这个IP和端口 使用以下命令: git config --global h…...
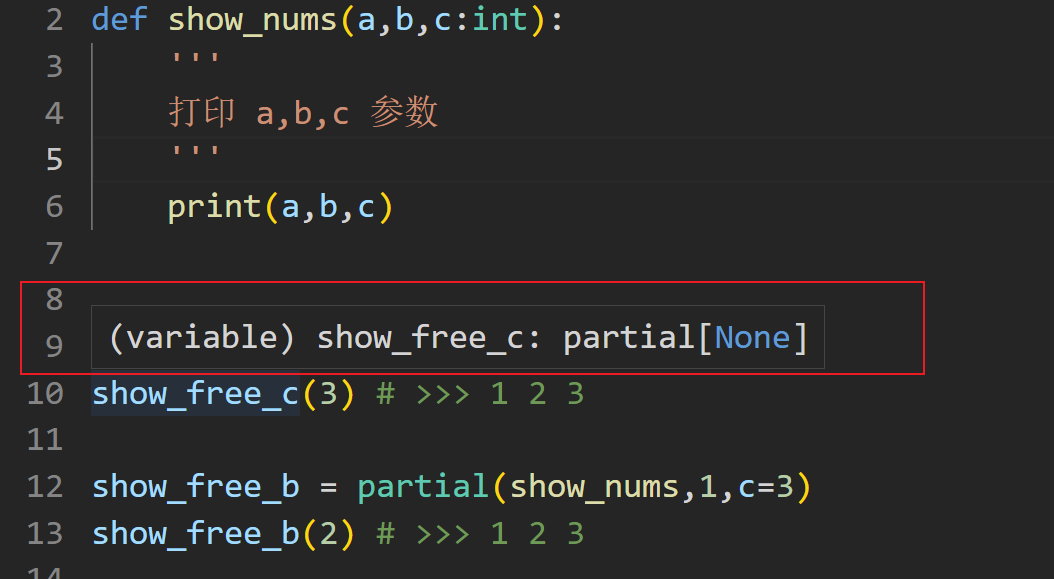
Python小技巧:冻结参数,让你的代码变简洁
Python 有一些非常使用的模块, functools 就是其中之一。今天我们来说说其中的 partial 函数, partial 函数看起来平平无奇,如果你经常翻看高手们写的库,会发现很多地方都在使用这函数。 入门 我们从一个小场景开始。 现在我们需…...

如何判断电脑电源质量的好坏?
电脑电源作为电脑的关键部件直接影响到电脑的性能和寿命,因此选择一个好的电源至关重要。那么要如何判断电脑电源的好坏呢?判断的指标都有哪些呢? 1.外观检测 观察电源外观可以初步判断电脑电源的工艺质量和材料质量。外观检测需要检查电源外壳是否坚固࿰…...

装饰器基础知识
一、概述 装饰器是可调用的对象,其参数是另一个函数(被装饰的函数)。装饰器可能会处理被装饰的函数,然后把它返回,或者将其替换成另一个函数或可调用对象。 装饰器的一大特性是,能把被装饰的函数替换成其他…...
轻量封装WebGPU渲染系统示例<42>- vsm阴影实现过程(源码)
前向实时渲染vsm阴影实现的主要步骤: 1. 编码深度数据,存到一个rtt中。 2. 纵向和横向执行遮挡信息blur filter sampling, 存到对应的rtt中。 3. 将上一步的结果(rtt)应用到可接收阴影的材质中。 具体代码情况文章最后附上的实现源码。 当前示例源码github地址: …...

[Electron] 将应用日志文件输出
日志文件输出可以使用 electron-log 模块。 electron-log 是一个用于 Electron 应用程序的日志记录库。它提供了一种简单且方便的方式来在 Electron 应用中记录日志信息,并支持将日志输出到文件、控制台和其他自定义目标。 以下是 electron-log 的一些主要特点…...

特性【C#】
C#特性是一种用于在编译时向程序元素添加声明性信息的语言结构。 下面是C#特性的使用方法: 1.使用系统提供的特性: 可以使用系统提供的特性来标记类、方法、属性等,以便在编译时进行验证或者提供其他信息。例如,可以使用Obsole…...

理解SpringIOC和DI第一课(Spring的特点),IOC对应五大注解,ApplicationContext vs BeanFactory
Spring是一个包含众多工具等Ioc容器 对象这个词在Spring范围内,称为bean Spring两大核心思想 1.IOC (IOC是控制反转,意思是控制权反转-控制权(正常是谁用这个对象,谁去创建,)-控制对象的控制权…...

【微服务】分布式限流如何实现
Sentinel 是一款阿里巴巴开源的分布式系统级流量控制组件,它提供了流量的自适应控制、熔断降级、系统负载保护等功能。下面是使用 Sentinel 实现分布式限流方案的基本步骤: 引入 Sentinel 依赖:首先在你的 Java 项目中引入 Sentinel 的相关依…...
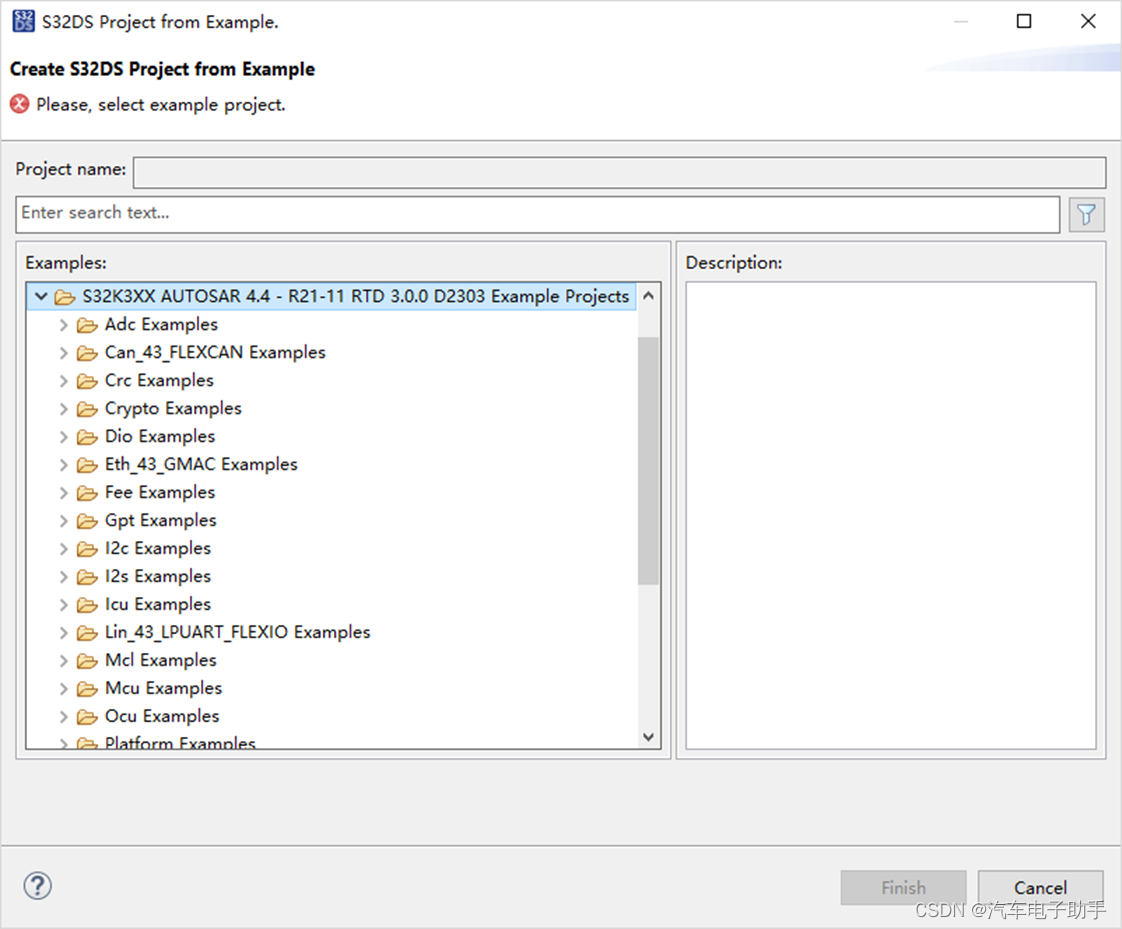
【S32K3环境搭建】-0.3-S32DS安装实时驱动RTD(Real-Time Driver)
目录 1 什么是“实时驱动RTD(Real-Time Driver)” 2 安装“实时驱动RTD(Real-Time Driver)” 2.1 方法一:通过S32DS Extensions and Updates安装“实时驱动RTD(Real-Time Driver)” 2.2 方法二:通过Install New Software…安装“实时驱动RTD(Real-Ti…...

软件设计之适配器模式
类模式 我们知道插座的电压为交流电220V,而日常电器使用的是直流电且电压会较小,比如手机充电会通过插头适配器达到额定的输入电流。下面我们实现这个案例:将220V电压转化为5V的电压。 package Adapter.Class;public class Adapter extends …...

虚拟化逻辑架构:OVS 交换机与端口管理
目录 一、实验 1.OVS 交换机管理 2.OVS端口管理 二、问题 1.KVM下的br0和virbr0有何区别 2.OVS 虚拟交换机 与接口如何实现关联的创建和删除 3.两个ovs之间如何进行流量交互 4.虚拟网络如何和物理网络互联 一、实验 1.OVS 交换机管理 (1)查看网…...

【springboot】idea项目启动端口被占用
问题 idea本地启动springboot项目端口老是被占用 解决 关闭被占用的端口进程 步骤: 1. winR打开程序框 2. 查出被占用端口的进程id netstat -ano | finderstr 端口号 例如 netstat -ano | finderstr 81013.杀死进程 taskkill /pid 进程id -t -f 例如 taskkill /pid 2…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...

rm视觉学习1-自瞄部分
首先先感谢中南大学的开源,提供了很全面的思路,减少了很多基础性的开发研究 我看的阅读的是中南大学FYT战队开源视觉代码 链接:https://github.com/CSU-FYT-Vision/FYT2024_vision.git 1.框架: 代码框架结构:readme有…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...

【java】【服务器】线程上下文丢失 是指什么
目录 ■前言 ■正文开始 线程上下文的核心组成部分 为什么会出现上下文丢失? 直观示例说明 为什么上下文如此重要? 解决上下文丢失的关键 总结 ■如果我想在servlet中使用线程,代码应该如何实现 推荐方案:使用 ManagedE…...

(12)-Fiddler抓包-Fiddler设置IOS手机抓包
1.简介 Fiddler不但能截获各种浏览器发出的 HTTP 请求,也可以截获各种智能手机发出的HTTP/ HTTPS 请求。 Fiddler 能捕获Android 和 Windows Phone 等设备发出的 HTTP/HTTPS 请求。同理也可以截获iOS设备发出的请求,比如 iPhone、iPad 和 MacBook 等苹…...
