[足式机器人]Part2 Dr. CAN学习笔记-Ch0-1矩阵的导数运算
本文仅供学习使用
本文参考:
B站:DR_CAN
Dr. CAN学习笔记-Ch0-1矩阵的导数运算
- 1. 标量向量方程对向量求导,分母布局,分子布局
- 1.1 标量方程对向量的导数
- 1.2 向量方程对向量的导数
- 2. 案例分析,线性回归
- 3. 矩阵求导的链式法则
1. 标量向量方程对向量求导,分母布局,分子布局
1.1 标量方程对向量的导数
- y y y 为 一元向量 或 二元向量
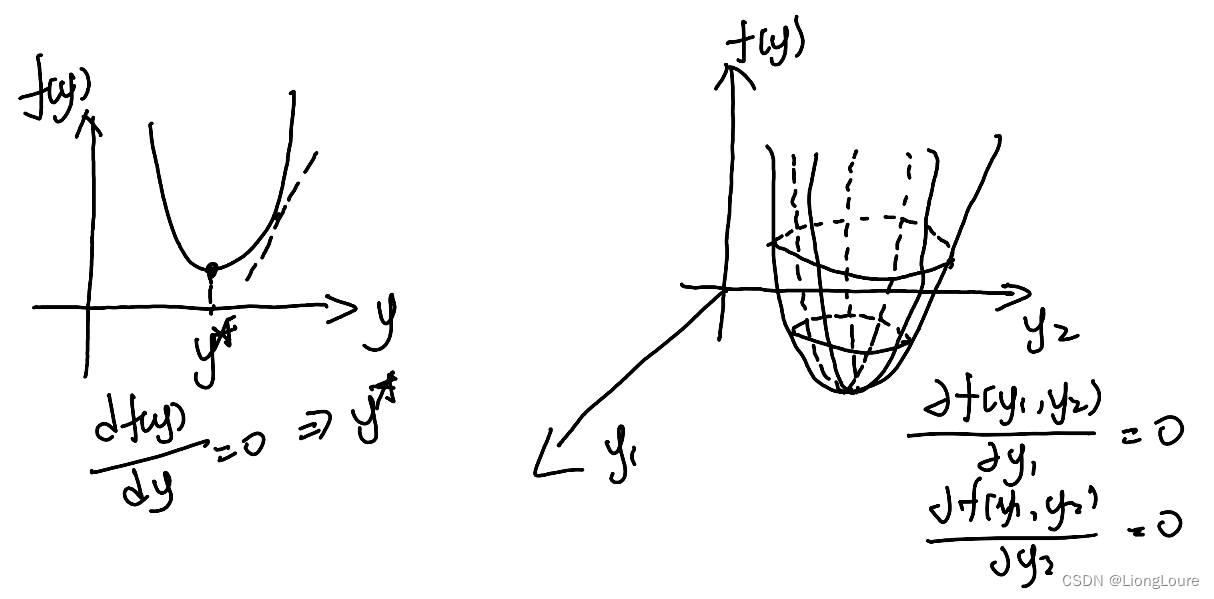
- y y y为多元向量
y ⃗ = [ y 1 , y 2 , ⋯ , y n ] ⇒ ∂ f ( y ⃗ ) ∂ y ⃗ \vec{y}=\left[ y_1,y_2,\cdots ,y_{\mathrm{n}} \right] \Rightarrow \frac{\partial f\left( \vec{y} \right)}{\partial \vec{y}} y=[y1,y2,⋯,yn]⇒∂y∂f(y)
其中: f ( y ⃗ ) f\left( \vec{y} \right) f(y) 为标量 1 × 1 1\times 1 1×1, y ⃗ \vec{y} y为向量 1 × n 1\times n 1×n
分母布局 Denominator Layout——行数与分母相同
∂ f ( y ⃗ ) ∂ y ⃗ = [ ∂ f ( y ⃗ ) ∂ y 1 ⋮ ∂ f ( y ⃗ ) ∂ y n ] n × 1 \frac{\partial f\left( \vec{y} \right)}{\partial \vec{y}}=\left[ \begin{array}{c} \frac{\partial f\left( \vec{y} \right)}{\partial y_1}\\ \vdots\\ \frac{\partial f\left( \vec{y} \right)}{\partial y_{\mathrm{n}}}\\ \end{array} \right] _{n\times 1} ∂y∂f(y)= ∂y1∂f(y)⋮∂yn∂f(y) n×1分子布局 Nunerator Layout——行数与分子相同
∂ f ( y ⃗ ) ∂ y ⃗ = [ ∂ f ( y ⃗ ) ∂ y 1 ⋯ ∂ f ( y ⃗ ) ∂ y n ] 1 × n \frac{\partial f\left( \vec{y} \right)}{\partial \vec{y}}=\left[ \begin{matrix} \frac{\partial f\left( \vec{y} \right)}{\partial y_1}& \cdots& \frac{\partial f\left( \vec{y} \right)}{\partial y_{\mathrm{n}}}\\ \end{matrix} \right] _{1\times n} ∂y∂f(y)=[∂y1∂f(y)⋯∂yn∂f(y)]1×n
1.2 向量方程对向量的导数
f ⃗ ( y ⃗ ) = [ f ⃗ 1 ( y ⃗ ) ⋮ f ⃗ n ( y ⃗ ) ] n × 1 , y ⃗ = [ y 1 ⋮ y m ] m × 1 \vec{f}\left( \vec{y} \right) =\left[ \begin{array}{c} \vec{f}_1\left( \vec{y} \right)\\ \vdots\\ \vec{f}_{\mathrm{n}}\left( \vec{y} \right)\\ \end{array} \right] _{n\times 1},\vec{y}=\left[ \begin{array}{c} y_1\\ \vdots\\ y_{\mathrm{m}}\\ \end{array} \right] _{\mathrm{m}\times 1} f(y)= f1(y)⋮fn(y) n×1,y= y1⋮ym m×1
∂ f ⃗ ( y ⃗ ) n × 1 ∂ y ⃗ m × 1 = [ ∂ f ⃗ ( y ⃗ ) ∂ y 1 ⋮ ∂ f ⃗ ( y ⃗ ) ∂ y m ] m × 1 = [ ∂ f 1 ( y ⃗ ) ∂ y 1 ⋯ ∂ f n ( y ⃗ ) ∂ y 1 ⋮ ⋱ ⋮ ∂ f 1 ( y ⃗ ) ∂ y m ⋯ ∂ f n ( y ⃗ ) ∂ y m ] m × n \frac{\partial \vec{f}\left( \vec{y} \right) _{n\times 1}}{\partial \vec{y}_{\mathrm{m}\times 1}}=\left[ \begin{array}{c} \frac{\partial \vec{f}\left( \vec{y} \right)}{\partial y_1}\\ \vdots\\ \frac{\partial \vec{f}\left( \vec{y} \right)}{\partial y_{\mathrm{m}}}\\ \end{array} \right] _{\mathrm{m}\times 1}=\left[ \begin{matrix} \frac{\partial f_1\left( \vec{y} \right)}{\partial y_1}& \cdots& \frac{\partial f_{\mathrm{n}}\left( \vec{y} \right)}{\partial y_1}\\ \vdots& \ddots& \vdots\\ \frac{\partial f_1\left( \vec{y} \right)}{\partial y_{\mathrm{m}}}& \cdots& \frac{\partial f_{\mathrm{n}}\left( \vec{y} \right)}{\partial y_{\mathrm{m}}}\\ \end{matrix} \right] _{\mathrm{m}\times \mathrm{n}} ∂ym×1∂f(y)n×1= ∂y1∂f(y)⋮∂ym∂f(y) m×1= ∂y1∂f1(y)⋮∂ym∂f1(y)⋯⋱⋯∂y1∂fn(y)⋮∂ym∂fn(y) m×n, 为分母布局
若: y ⃗ = [ y 1 ⋮ y m ] m × 1 , A = [ a 11 ⋯ a 1 n ⋮ ⋱ ⋮ a m 1 ⋯ a m n ] \vec{y}=\left[ \begin{array}{c} y_1\\ \vdots\\ y_{\mathrm{m}}\\ \end{array} \right] _{\mathrm{m}\times 1}, A=\left[ \begin{matrix} a_{11}& \cdots& a_{1\mathrm{n}}\\ \vdots& \ddots& \vdots\\ a_{\mathrm{m}1}& \cdots& a_{\mathrm{mn}}\\ \end{matrix} \right] y= y1⋮ym m×1,A= a11⋮am1⋯⋱⋯a1n⋮amn , 则有:
- ∂ A y ⃗ ∂ y ⃗ = A T \frac{\partial A\vec{y}}{\partial \vec{y}}=A^{\mathrm{T}} ∂y∂Ay=AT(分母布局)
- ∂ y ⃗ T A y ⃗ ∂ y ⃗ = A y ⃗ + A T y ⃗ \frac{\partial \vec{y}^{\mathrm{T}}A\vec{y}}{\partial \vec{y}}=A\vec{y}+A^{\mathrm{T}}\vec{y} ∂y∂yTAy=Ay+ATy, 当 A = A T A=A^{\mathrm{T}} A=AT时, ∂ y ⃗ T A y ⃗ ∂ y ⃗ = 2 A y ⃗ \frac{\partial \vec{y}^{\mathrm{T}}A\vec{y}}{\partial \vec{y}}=2A\vec{y} ∂y∂yTAy=2Ay
若为分子布局,则有: ∂ A y ⃗ ∂ y ⃗ = A \frac{\partial A\vec{y}}{\partial \vec{y}}=A ∂y∂Ay=A
2. 案例分析,线性回归
- ∂ A y ⃗ ∂ y ⃗ = A T \frac{\partial A\vec{y}}{\partial \vec{y}}=A^{\mathrm{T}} ∂y∂Ay=AT(分母布局)
- ∂ y ⃗ T A y ⃗ ∂ y ⃗ = A y ⃗ + A T y ⃗ \frac{\partial \vec{y}^{\mathrm{T}}A\vec{y}}{\partial \vec{y}}=A\vec{y}+A^{\mathrm{T}}\vec{y} ∂y∂yTAy=Ay+ATy, 当 A = A T A=A^{\mathrm{T}} A=AT时, ∂ y ⃗ T A y ⃗ ∂ y ⃗ = 2 A y ⃗ \frac{\partial \vec{y}^{\mathrm{T}}A\vec{y}}{\partial \vec{y}}=2A\vec{y} ∂y∂yTAy=2Ay
Linear Regression 线性回归
z ^ = y 1 + y 2 x ⇒ J = ∑ i = 1 n [ z i − ( y 1 + y 2 x i ) ] 2 \hat{z}=y_1+y_2x\Rightarrow J=\sum_{i=1}^n{\left[ z_i-\left( y_1+y_2x_i \right) \right] ^2} z^=y1+y2x⇒J=i=1∑n[zi−(y1+y2xi)]2
找到 y 1 , y 2 y_1,y_2 y1,y2 使得 J J J最小
z ⃗ = [ z 1 ⋮ z n ] , [ x ⃗ ] = [ 1 x 1 ⋮ ⋮ 1 x n ] , y ⃗ = [ y 1 y 2 ] ⇒ z ⃗ ^ = [ x ⃗ ] y ⃗ = [ y 1 + y 2 x 1 ⋮ y 1 + y 2 x n ] \vec{z}=\left[ \begin{array}{c} z_1\\ \vdots\\ z_{\mathrm{n}}\\ \end{array} \right] ,\left[ \vec{x} \right] =\left[ \begin{array}{l} 1& x_1\\ \vdots& \vdots\\ 1& x_{\mathrm{n}}\\ \end{array} \right] ,\vec{y}=\left[ \begin{array}{c} y_1\\ y_2\\ \end{array} \right] \Rightarrow \hat{\vec{z}}=\left[ \vec{x} \right] \vec{y}=\left[ \begin{array}{c} y_1+y_2x_1\\ \vdots\\ y_1+y_2x_{\mathrm{n}}\\ \end{array} \right] z= z1⋮zn ,[x]= 1⋮1x1⋮xn ,y=[y1y2]⇒z^=[x]y= y1+y2x1⋮y1+y2xn
J = [ z ⃗ − z ⃗ ^ ] T [ z ⃗ − z ⃗ ^ ] = [ z ⃗ − [ x ⃗ ] y ⃗ ] T [ z ⃗ − [ x ⃗ ] y ⃗ ] = z ⃗ z ⃗ T − z ⃗ T [ x ⃗ ] y ⃗ − y ⃗ T [ x ⃗ ] T z ⃗ + y ⃗ T [ x ⃗ ] T [ x ⃗ ] y ⃗ J=\left[ \vec{z}-\hat{\vec{z}} \right] ^{\mathrm{T}}\left[ \vec{z}-\hat{\vec{z}} \right] =\left[ \vec{z}-\left[ \vec{x} \right] \vec{y} \right] ^{\mathrm{T}}\left[ \vec{z}-\left[ \vec{x} \right] \vec{y} \right] =\vec{z}\vec{z}^{\mathrm{T}}-\vec{z}^{\mathrm{T}}\left[ \vec{x} \right] \vec{y}-\vec{y}^{\mathrm{T}}\left[ \vec{x} \right] ^{\mathrm{T}}\vec{z}+\vec{y}^{\mathrm{T}}\left[ \vec{x} \right] ^{\mathrm{T}}\left[ \vec{x} \right] \vec{y} J=[z−z^]T[z−z^]=[z−[x]y]T[z−[x]y]=zzT−zT[x]y−yT[x]Tz+yT[x]T[x]y
其中: ( z ⃗ T [ x ⃗ ] y ⃗ ) T = y ⃗ T [ x ⃗ ] T z ⃗ \left( \vec{z}^{\mathrm{T}}\left[ \vec{x} \right] \vec{y} \right) ^{\mathrm{T}}=\vec{y}^{\mathrm{T}}\left[ \vec{x} \right] ^{\mathrm{T}}\vec{z} (zT[x]y)T=yT[x]Tz, 则有:
J = z ⃗ z ⃗ T − 2 z ⃗ T [ x ⃗ ] y ⃗ + y ⃗ T [ x ⃗ ] T [ x ⃗ ] y ⃗ J=\vec{z}\vec{z}^{\mathrm{T}}-2\vec{z}^{\mathrm{T}}\left[ \vec{x} \right] \vec{y}+\vec{y}^{\mathrm{T}}\left[ \vec{x} \right] ^{\mathrm{T}}\left[ \vec{x} \right] \vec{y} J=zzT−2zT[x]y+yT[x]T[x]y
进而:
∂ J ∂ y ⃗ = 0 − 2 ( z ⃗ T [ x ⃗ ] ) T + 2 [ x ⃗ ] T [ x ⃗ ] y ⃗ = ∇ y ⃗ ⟹ ∂ J ∂ y ⃗ ∗ = 0 , y ⃗ ∗ = ( [ x ⃗ ] T [ x ⃗ ] ) − 1 [ x ⃗ ] T z ⃗ \frac{\partial J}{\partial \vec{y}}=0-2\left( \vec{z}^{\mathrm{T}}\left[ \vec{x} \right] \right) ^{\mathrm{T}}+2\left[ \vec{x} \right] ^{\mathrm{T}}\left[ \vec{x} \right] \vec{y}=\nabla \vec{y}\Longrightarrow \frac{\partial J}{\partial \vec{y}^*}=0,\vec{y}^*=\left( \left[ \vec{x} \right] ^{\mathrm{T}}\left[ \vec{x} \right] \right) ^{-1}\left[ \vec{x} \right] ^{\mathrm{T}}\vec{z} ∂y∂J=0−2(zT[x])T+2[x]T[x]y=∇y⟹∂y∗∂J=0,y∗=([x]T[x])−1[x]Tz
其中: ( [ x ⃗ ] T [ x ⃗ ] ) − 1 \left( \left[ \vec{x} \right] ^{\mathrm{T}}\left[ \vec{x} \right] \right) ^{-1} ([x]T[x])−1不一定有解,则 y ⃗ ∗ \vec{y}^* y∗无法得到解析解——定义初始 y ⃗ ∗ \vec{y}^* y∗, y ⃗ ∗ = y ⃗ ∗ − α ∇ , α = [ α 1 0 0 α 2 ] \vec{y}^*=\vec{y}^*-\alpha \nabla ,\alpha =\left[ \begin{matrix} \alpha _1& 0\\ 0& \alpha _2\\ \end{matrix} \right] y∗=y∗−α∇,α=[α100α2]
其中: α \alpha α称为学习率,对 x x x而言则需进行归一化
3. 矩阵求导的链式法则
标量函数: J = f ( y ( u ) ) , ∂ J ∂ u = ∂ J ∂ y ∂ y ∂ u J=f\left( y\left( u \right) \right) ,\frac{\partial J}{\partial u}=\frac{\partial J}{\partial y}\frac{\partial y}{\partial u} J=f(y(u)),∂u∂J=∂y∂J∂u∂y
标量对向量求导: J = f ( y ⃗ ( u ⃗ ) ) , y ⃗ = [ y 1 ( u ⃗ ) ⋮ y m ( u ⃗ ) ] m × 1 , u ⃗ = [ u ⃗ 1 ⋮ u ⃗ n ] n × 1 J=f\left( \vec{y}\left( \vec{u} \right) \right) ,\vec{y}=\left[ \begin{array}{c} y_1\left( \vec{u} \right)\\ \vdots\\ y_{\mathrm{m}}\left( \vec{u} \right)\\ \end{array} \right] _{m\times 1},\vec{u}=\left[ \begin{array}{c} \vec{u}_1\\ \vdots\\ \vec{u}_{\mathrm{n}}\\ \end{array} \right] _{\mathrm{n}\times 1} J=f(y(u)),y= y1(u)⋮ym(u) m×1,u= u1⋮un n×1
分析: ∂ J 1 × 1 ∂ u n × 1 n × 1 = ∂ J ∂ y m × 1 m × 1 ∂ y m × 1 ∂ u n × 1 n × m \frac{\partial J_{1\times 1}}{\partial u_{\mathrm{n}\times 1}}_{\mathrm{n}\times 1}=\frac{\partial J}{\partial y_{m\times 1}}_{m\times 1}\frac{\partial y_{m\times 1}}{\partial u_{\mathrm{n}\times 1}}_{\mathrm{n}\times \mathrm{m}} ∂un×1∂J1×1n×1=∂ym×1∂Jm×1∂un×1∂ym×1n×m 无法相乘
y ⃗ = [ y 1 ( u ⃗ ) y 2 ( u ⃗ ) ] 2 × 1 , u ⃗ = [ u ⃗ 1 u ⃗ 2 u ⃗ 3 ] 3 × 1 \vec{y}=\left[ \begin{array}{c} y_1\left( \vec{u} \right)\\ y_2\left( \vec{u} \right)\\ \end{array} \right] _{2\times 1},\vec{u}=\left[ \begin{array}{c} \vec{u}_1\\ \vec{u}_2\\ \vec{u}_3\\ \end{array} \right] _{3\times 1} y=[y1(u)y2(u)]2×1,u= u1u2u3 3×1
J = f ( y ⃗ ( u ⃗ ) ) , ∂ J ∂ u ⃗ = [ ∂ J ∂ u ⃗ 1 ∂ J ∂ u ⃗ 2 ∂ J ∂ u ⃗ 3 ] 3 × 1 ⟹ ∂ J ∂ u ⃗ 1 = ∂ J ∂ y 1 ∂ y 1 ( u ⃗ ) ∂ u ⃗ 1 + ∂ J ∂ y 2 ∂ y 2 ( u ⃗ ) ∂ u ⃗ 1 ∂ J ∂ u ⃗ 2 = ∂ J ∂ y 1 ∂ y 1 ( u ⃗ ) ∂ u ⃗ 2 + ∂ J ∂ y 2 ∂ y 2 ( u ⃗ ) ∂ u ⃗ 2 ∂ J ∂ u ⃗ 3 = ∂ J ∂ y 1 ∂ y 1 ( u ⃗ ) ∂ u ⃗ 3 + ∂ J ∂ y 2 ∂ y 2 ( u ⃗ ) ∂ u ⃗ 3 ⟹ ∂ J ∂ u ⃗ = [ ∂ y 1 ( u ⃗ ) ∂ u ⃗ 1 ∂ y 2 ( u ⃗ ) ∂ u ⃗ 1 ∂ y 1 ( u ⃗ ) ∂ u ⃗ 2 ∂ y 2 ( u ⃗ ) ∂ u ⃗ 2 ∂ y 1 ( u ⃗ ) ∂ u ⃗ 3 ∂ y 2 ( u ⃗ ) ∂ u ⃗ 3 ] 3 × 2 [ ∂ J ∂ y 1 ∂ J ∂ y 2 ] 2 × 2 = ∂ y ⃗ ( u ⃗ ) ∂ u ⃗ ∂ J ∂ y ⃗ J=f\left( \vec{y}\left( \vec{u} \right) \right) ,\frac{\partial J}{\partial \vec{u}}=\left[ \begin{array}{c} \frac{\partial J}{\partial \vec{u}_1}\\ \frac{\partial J}{\partial \vec{u}_2}\\ \frac{\partial J}{\partial \vec{u}_3}\\ \end{array} \right] _{3\times 1}\Longrightarrow \begin{array}{c} \frac{\partial J}{\partial \vec{u}_1}=\frac{\partial J}{\partial y_1}\frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_1}+\frac{\partial J}{\partial y_2}\frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_1}\\ \frac{\partial J}{\partial \vec{u}_2}=\frac{\partial J}{\partial y_1}\frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_2}+\frac{\partial J}{\partial y_2}\frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_2}\\ \frac{\partial J}{\partial \vec{u}_3}=\frac{\partial J}{\partial y_1}\frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_3}+\frac{\partial J}{\partial y_2}\frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_3}\\ \end{array} \\ \Longrightarrow \frac{\partial J}{\partial \vec{u}}=\left[ \begin{array}{l} \frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_1}& \frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_1}\\ \frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_2}& \frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_2}\\ \frac{\partial y_1\left( \vec{u} \right)}{\partial \vec{u}_3}& \frac{\partial y_2\left( \vec{u} \right)}{\partial \vec{u}_3}\\ \end{array} \right] _{3\times 2}\left[ \begin{array}{c} \frac{\partial J}{\partial y_1}\\ \frac{\partial J}{\partial y_2}\\ \end{array} \right] _{2\times 2}=\frac{\partial \vec{y}\left( \vec{u} \right)}{\partial \vec{u}}\frac{\partial J}{\partial \vec{y}} J=f(y(u)),∂u∂J= ∂u1∂J∂u2∂J∂u3∂J 3×1⟹∂u1∂J=∂y1∂J∂u1∂y1(u)+∂y2∂J∂u1∂y2(u)∂u2∂J=∂y1∂J∂u2∂y1(u)+∂y2∂J∂u2∂y2(u)∂u3∂J=∂y1∂J∂u3∂y1(u)+∂y2∂J∂u3∂y2(u)⟹∂u∂J= ∂u1∂y1(u)∂u2∂y1(u)∂u3∂y1(u)∂u1∂y2(u)∂u2∂y2(u)∂u3∂y2(u) 3×2[∂y1∂J∂y2∂J]2×2=∂u∂y(u)∂y∂J
∂ J ∂ u ⃗ = ∂ y ⃗ ( u ⃗ ) ∂ u ⃗ ∂ J ∂ y ⃗ \frac{\partial J}{\partial \vec{u}}=\frac{\partial \vec{y}\left( \vec{u} \right)}{\partial \vec{u}}\frac{\partial J}{\partial \vec{y}} ∂u∂J=∂u∂y(u)∂y∂J
eg:
x ⃗ [ k + 1 ] = A x ⃗ [ k ] + B u ⃗ [ k ] , J = x ⃗ T [ k + 1 ] x ⃗ [ k + 1 ] \vec{x}\left[ k+1 \right] =A\vec{x}\left[ k \right] +B\vec{u}\left[ k \right] ,J=\vec{x}^{\mathrm{T}}\left[ k+1 \right] \vec{x}\left[ k+1 \right] x[k+1]=Ax[k]+Bu[k],J=xT[k+1]x[k+1]
∂ J ∂ u ⃗ = ∂ x ⃗ [ k + 1 ] ∂ u ⃗ ∂ J ∂ x ⃗ [ k + 1 ] = B T ⋅ 2 x ⃗ [ k + 1 ] = 2 B T x ⃗ [ k + 1 ] \frac{\partial J}{\partial \vec{u}}=\frac{\partial \vec{x}\left[ k+1 \right]}{\partial \vec{u}}\frac{\partial J}{\partial \vec{x}\left[ k+1 \right]}=B^{\mathrm{T}}\cdot 2\vec{x}\left[ k+1 \right] =2B^{\mathrm{T}}\vec{x}\left[ k+1 \right] ∂u∂J=∂u∂x[k+1]∂x[k+1]∂J=BT⋅2x[k+1]=2BTx[k+1]
相关文章:

[足式机器人]Part2 Dr. CAN学习笔记-Ch0-1矩阵的导数运算
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记-Ch0-1矩阵的导数运算 1. 标量向量方程对向量求导,分母布局,分子布局1.1 标量方程对向量的导数1.2 向量方程对向量的导数 2. 案例分析,线性回归3. 矩阵求导的链…...
如何让软文更具画面感,媒介盒子分享
写软文这种带有销售性质的文案时,总说要有画面感,要有想象空间。只有针对目标用户的感受的设计,要了解用户想的是什么,要用可视化的描述来影响用户的感受,今天媒介盒子就和大家分享:如何让软文更具画面感。…...

Hadoop学习笔记(HDP)-Part.19 安装Kafka
目录 Part.01 关于HDP Part.02 核心组件原理 Part.03 资源规划 Part.04 基础环境配置 Part.05 Yum源配置 Part.06 安装OracleJDK Part.07 安装MySQL Part.08 部署Ambari集群 Part.09 安装OpenLDAP Part.10 创建集群 Part.11 安装Kerberos Part.12 安装HDFS Part.13 安装Ranger …...

Arrays类练习 - Java
案例:自定义Book类,里面包含name和price,按price排序(从大到小)。要求使用两种方式排序,有一个 Book[] books 4本书对象。 使用前面学习过的传递实现Comparator接口匿名内部类,也称为定制排序。可以按照price (1)从大到…...

Java多线程:代码不只是在‘Hello World‘
Java线程好书推荐 概述01 多线程对于Java的意义02 为什么Java工程师必须掌握多线程03 Java多线程使用方式04 如何学好Java多线程写在末尾: 主页传送门:📀 传送 概述 摘要:互联网的每一个角落,无论是大型电商平台的秒杀…...

使用PCSS实现的实时阴影效果
PCSS的技术可以使得阴影呈现出近硬远软的效果,并且能够实时实现。 其核心理念是通过模拟光源的面积来产生更自然、更柔和的阴影边缘。 具体步骤: 1、生成shadowmap 2、在进行阴影的比较时候进行平均,并非之前的shadow map 或者之后完全的阴影…...
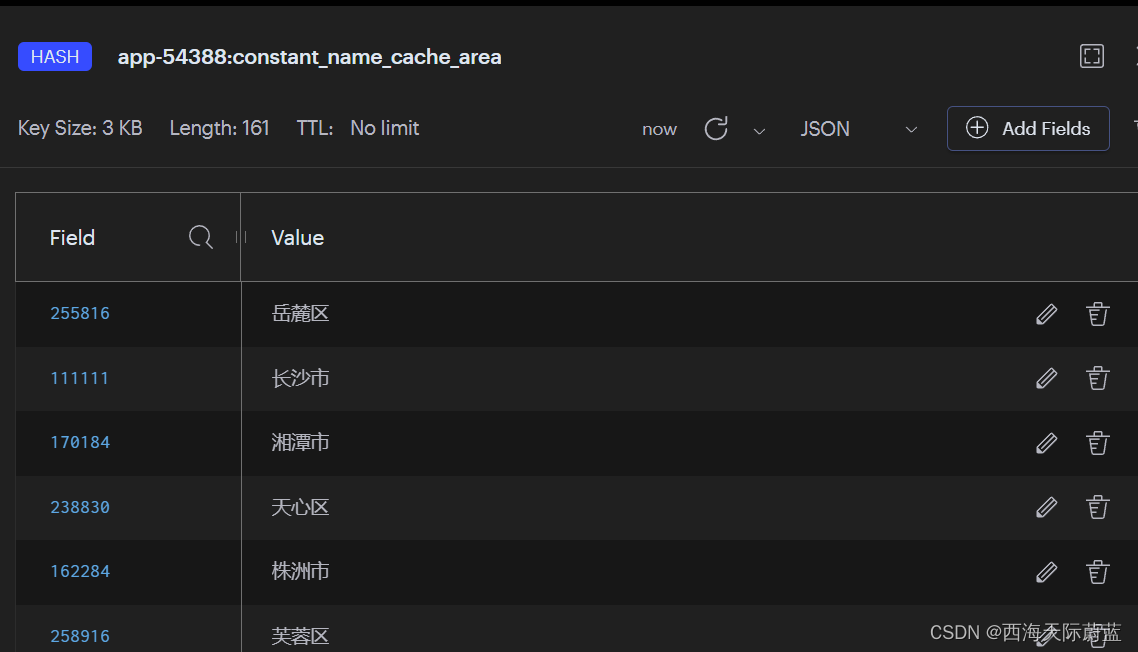
用于缓存一些固定名称的小组件
项目中,用于缓存姓名、地名、单位名称等一些较固定名称的id-name小组件。用于减少一些表的关连操作和冗余字段。优化代码结构。扩展也方便,写不同的枚举就行了。 具体用法: {NameCacheUser.USER.getName(userId);NameCacheUser.ACCOUNT.getN…...

Python 读取电子发票PDF 转成Excel
Python 读取电子发票PDF 转成Excel 目录 0.前提 1.python相关的处理PDF的库 2.实际好用的 3.实际代码 4.思考 0.前提 只识别普通电子发票PDF,提取其中某些关键内容到excel中。 1.python相关的处理PDF的库 如下4个库是经常更新维护的! pyP…...
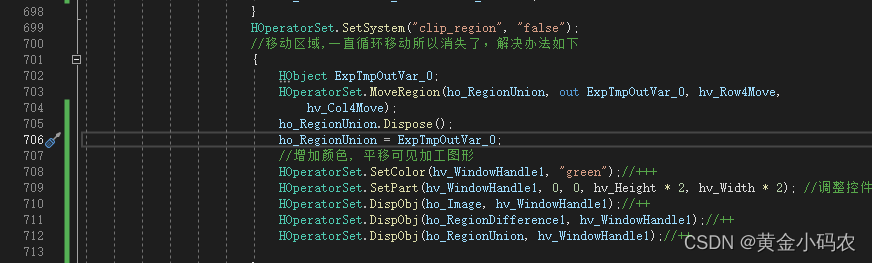
我的项目问题
1.一点缩放和旋转就消失,需要再次平移才出现 解决方案:在显示当前图形时,显示已有图形。 2.每次点击平移,图形移动到上次点击的位置。 ho_RegionUnion.Dispose(); ho_RegionUnion ExpTmpOutVar_0;这两段代码放到显示之后的&am…...
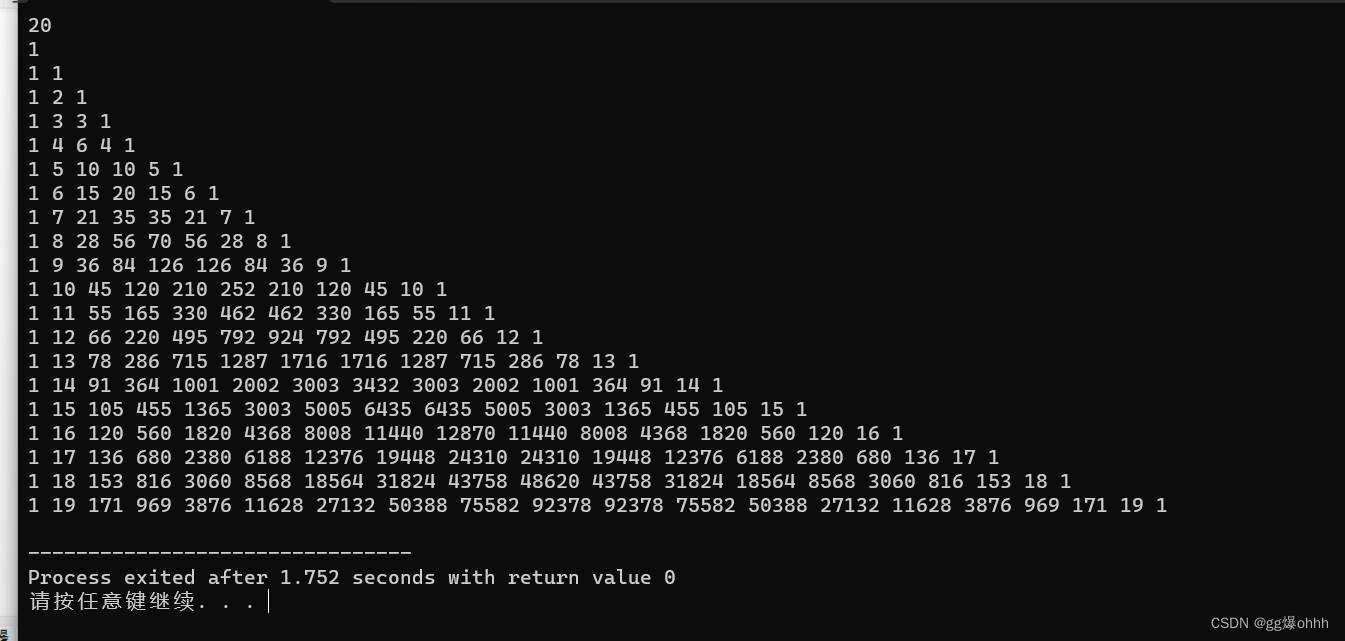
【c】杨辉三角
下面介绍两种方法 1.利用上面性质的第五条,我们可以求各行各列的组合数 2.利用上面性质的第7条,我们可以用数组完成 下面附上代码 1. #include<stdio.h> void fact(int n ,int m )//求组合数 {long long int sum11;long long int sum21;int a…...

算法刷题之数组篇
题目一:两数之和 给出一个整型数组 numbers 和一个目标值 target,请在数组中找出两个加起来等于目标值的数的下标,返回的下标按升序排列。 (注:返回的数组下标从1开始算起,保证target一定可以由数组里面2…...
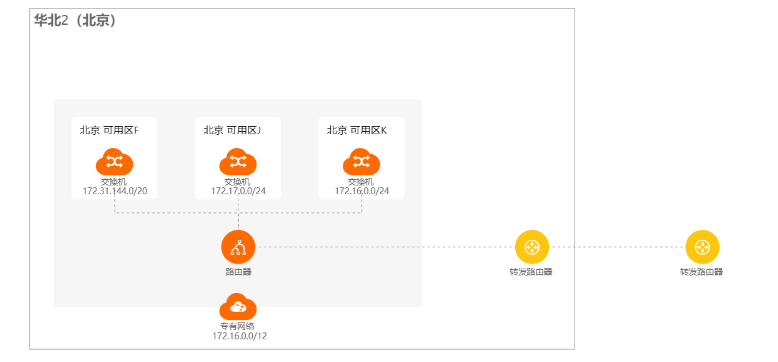
TR转发路由器测评—云企业网实现跨地域跨VPC的网络互通测评实战【阿里云产品测评】
文章目录 一.转发路由器 Transit Router 测评1.1 准备阶段1.2 本文测评收获1.3 什么是云企业网实例、转发路由器实例和云数据传输服务 二.使用云企业网实现跨地域跨VPC的网络互通2.2 **测试连通性**2.3 网络拓扑如下: 心得:总结: 声明&#x…...
1.1美术理论基础
一、光影 物体呈现在人们眼前的时候,不同的受光面其明暗变化以及物体的影子。 1.什么是黑白灰 在美术中黑白灰指亮面、灰面、暗面,属于素描的三大面,主要体验一个物体的整体寿光过程。普遍存在于各种艺术和设计领域。黑白灰作品的出现&#x…...

【Java 基础】21 多线程同步与锁
文章目录 1.存在的问题2.使用同步解决问题1) synchronized2) volatile3) 锁 总结 用多线程过程中,有可能出现 多个线程同时处理(获取或修改等)同一个数据,这个时候就 会发生数据不同步的问题, 因此出现了同步和锁来…...

Python语言基础知识(一)
文章目录 1、Python内置对象介绍2、标识符与变量3、数据类型—数字4、数据类型—字符串与字节串5、数据类型—列表、元组、字典、集合6、运算符和表达式7、运算符和表达式—算术运算符8、运算符和表达式—关系运算符9.1、运算符和表达式— 成员测试运算符in9.2、运算符和表达式…...
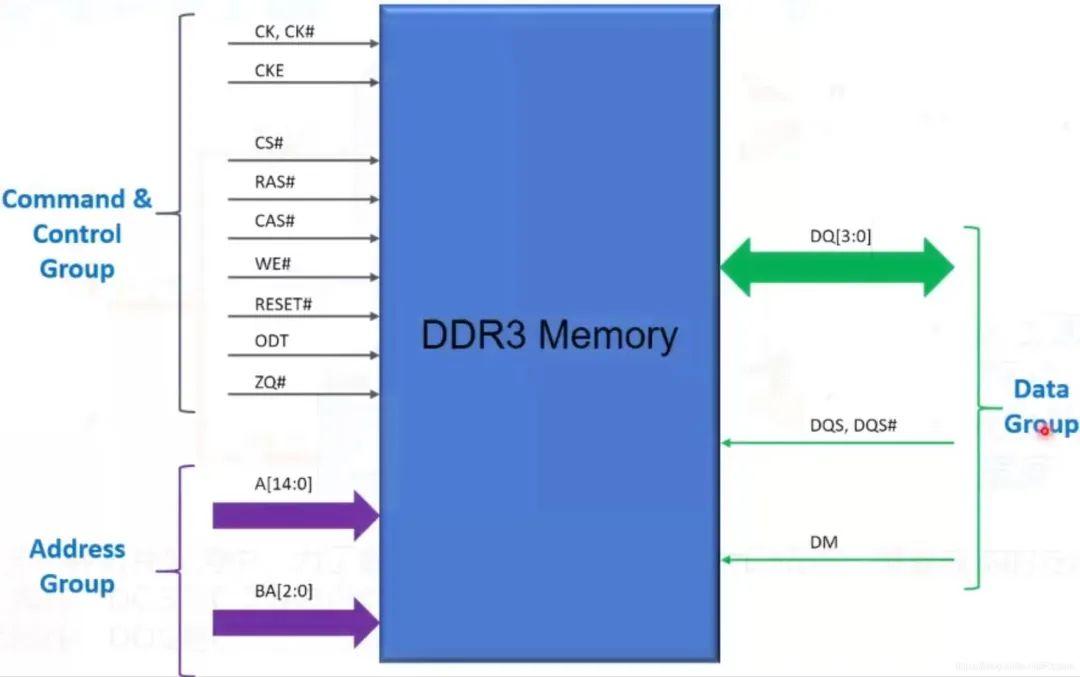
Xilinx FPGA平台DDR3设计详解(三):DDR3 介绍
本文介绍一下常用的存储芯片DDR3,包括DDR3的芯片型号识别、DDR3芯片命名、DDR3的基本结构等知识,为后续掌握FPGA DDR3的读写控制打下坚实基础。 一、DDR3芯片型号 电路板上的镁光DDR3芯片上没有具体的型号名。 如果想知道具体的DDR3芯片型号&#…...

字典的遍历
字典不是有序的集合,就不能通过index来遍历了,那如何遍历字典呢? 方法一:直接用字典 for key in a_dict: print a_dict[key] 通过这样的结构可以的。 d {"liming" : 98, "wangli":95, "mali":90, "liping&q…...
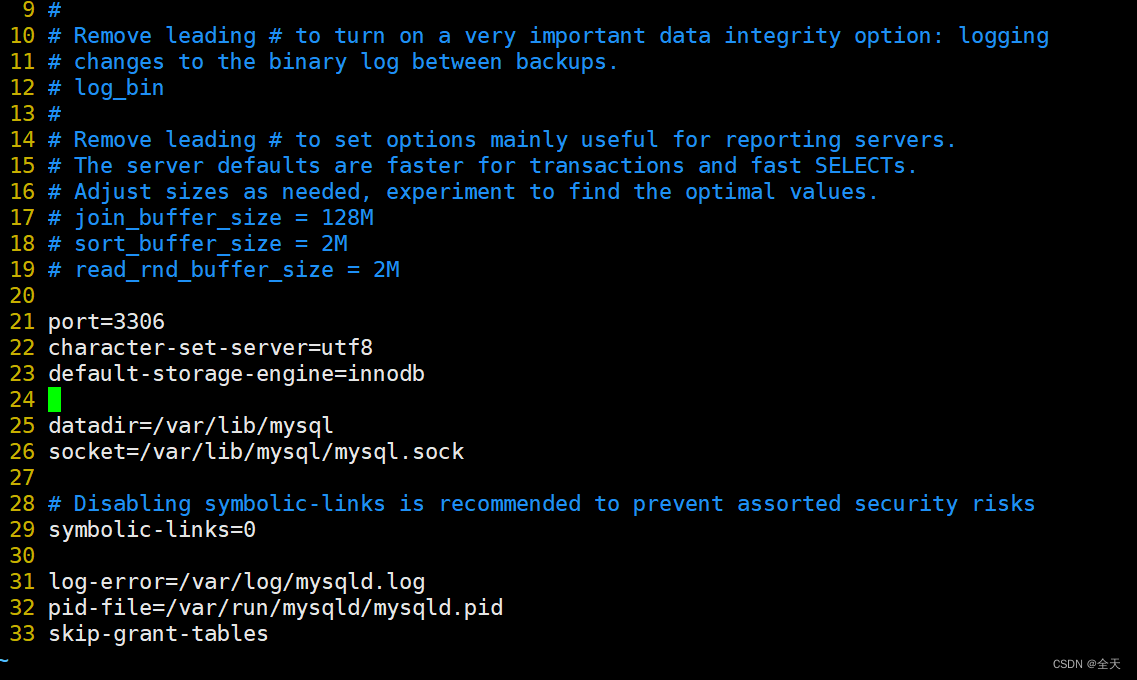
Linux环境下的MySQL安装
文章目录 前提说明1.卸载内置环境2.检查系统安装包3.卸载这些默认安装包4.获取MySQL官方yum源5.安装MySQLyum源,对比前后yum源6.查看yum源是否生效7.安装MySQL服务8.查看相对应的配置文件9.启动服务10.查看启动服务11.登录方法一12.登录方法二13.登录方法三14.设置开…...

梦想与魔法:编程之路的挑战与荣耀
在年少轻狂的岁月里,我们都有过一些不切实际的梦想,渴望成为某种神奇的存在。我的梦想是成为一名神奇的码农,用键盘编织魔法,创造出炫酷的虚拟世界。然而,现实是残酷的,当我刚入门计算机领域时,…...

qt 5.15.2 主窗体菜单工具栏树控件功能
qt 5.15.2 主窗体菜单工具栏树控件功能 显示主窗体效果: mainwindow.h文件内容: #ifndef MAINWINDOW_H #define MAINWINDOW_H#include <QMainWindow> #include <QFileDialog> #include <QString> #include <QMessageBox>#inc…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

基于江科大stm32屏幕驱动,实现OLED多级菜单(动画效果),结构体链表实现(独创源码)
引言 在嵌入式系统中,用户界面的设计往往直接影响到用户体验。本文将以STM32微控制器和OLED显示屏为例,介绍如何实现一个多级菜单系统。该系统支持用户通过按键导航菜单,执行相应操作,并提供平滑的滚动动画效果。 本文设计了一个…...
