南京大学考研机试题DP
3. dp 求子序列的个数
https://www.acwing.com/problem/content/description/3716/
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_set>
#include <vector>
using namespace std;
const int N = 1e4 + 10 , mod = 1000000007;
int T;
char s[N] , p[N];
int f[N];
int n , m;
/*
首先求公共子序列问题想到 DP
写出 F[i][j] 函数的含义:
s数组中由前i个字符构成的子序列 和P数组中前j个字符构成的子串构成的集合
// 字串和子序列不同的含义是字串是连续的 , 子序列可以不连续
分析状态转移:
1. 包含 s[i] 当且仅当 s[i] = p[j]
f[i][j] = f[i - 1][j - 1] 从上一个状态转移而来
上一个状态是由s中前 i - 1 个字符构成的子序列和 p 中前 j - 1 个字符构成的字串
2. 不包含 s[i] f[i][j] = f[i - 1][j]
优化空间
发现需要优化 f[i][j] = f[i - 1][j] + f[i - 1][j - 1]
我们发现 f[i][j] = f[i - 1][j] 从 i - 1 层计算得到
f[i][j] = f[i - 1][j - 1] 由 i - 1 层计算得到
如果我们从小到大枚举 j 那么 第 i - 1层的 f[j - 1] 会被 第 i 层的覆盖
所以 我们需要从 m - 0 枚举 j (为什么到 0 因为 f[0] 也是一种方案)
优化时间
分析时间复杂度 o(n ^ 2 * Q) > 1e9 我们依然是两维
其次我们发现依然 TLE
但我们知道 只有当 s[i] = p[j] 的时候才会更新
所以我们只需要将 s[i] = p[j] 的元素枚举即可
开一个 vector 存 b 中每一个字母出现的下标
第一层枚举 S 的时候只需要 第二层枚举 b[s[i] - 'a'] 也就是 p 和 s 相同的下标就可以了
*/
int main()
{
cin >> T;
while(T --)
{
cin >> s + 1 >> p + 1;
n = strlen(s + 1);
m = strlen(p + 1);
memset(f , 0 , sizeof f);
f[0] = 1;
vector<int> b[26];
for(int i = m ; i ; i --)
b[p[i] - 'a'].push_back(i);
for(int i = 1 ; i <= n ; i ++)
for(auto j : b[s[i] - 'a'])
{
if(s[i] == p[j])
f[j] = (f[j] + f[j - 1]) % mod;
}
cout << f[m] << endl;
}
return 0;
}
相关文章:

南京大学考研机试题DP
3. dp 求子序列的个数 https://www.acwing.com/problem/content/description/3716/ #include <iostream> #include <cstring> #include <algorithm> #include <unordered_set> #include <vector> using namespace std; const int N 1e4 10…...

如何进行多ip服务器租用?
如何进行多ip服务器租用? 对于网络时代来说,是需要很多设备才能维持的,比如说多ip服务器就是互联网时代常见的设备,所以我们需要对多ip服务器有足够的了解,这样才能更好的获取互联网上的信息,满足我们工作…...

(动手学习深度学习)第13章 实战kaggle竞赛:树叶分类
文章目录 实战kaggle比赛:树叶分类1. 导入相关库2. 查看数据格式3. 制作数据集4. 数据可视化5. 定义网络模型6. 定义超参数7. 训练模型8. 测试并提交文件 竞赛技术总结1. 技术分析2. 数据方面模型方面3. AutoGluon4. 总结 实战kaggle比赛:树叶分类 kagg…...

vue中shift+alt+f格式化防止格式掉其它内容
好处就是使得提交记录干净,否则修改一两行代码,习惯性按了一下格式化快捷键,遍地飘红,下次找修改就费时间 1.点击设置图标-设置 2.点击这个转成配置文件 {"extensions.ignoreRecommendations": true,"[vue]":…...
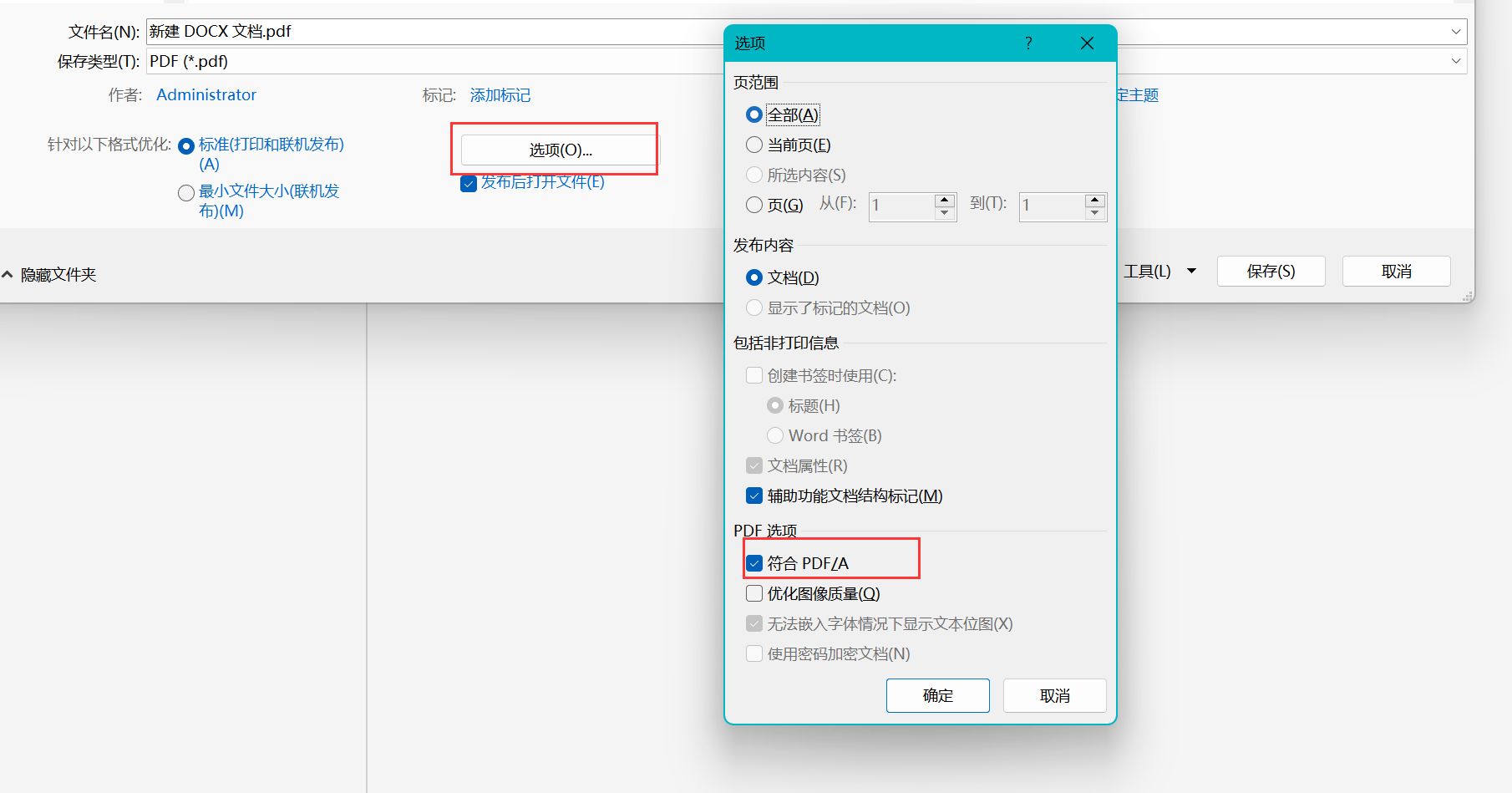
WPS导出的PDF比较糊,和原始的不太一样,将带有SVG的文档输出为PDF
一、在WPS的PPT中 你直接输出PDF可能会导致一些问题(比如照片比原来糊)/ 或者你复制PPT中的图片到AI中类似的操作,得到的照片比原来糊,所以应该选择打印-->高级打印 然后再另存为PDF 最后再使用AI打开PDF文件再复制到你想用…...

Linux /etc/hosts文件
Linux的 /etc/hosts 文件用于静态地映射主机名到 IP 地址。 通常用于本地网络中的名称解析,它可以覆盖 DNS 的设置。当你访问一个域名时,系统会首先检查 /etc/hosts 文件,如果找到了匹配项,就会使用该 IP 地址,否则会…...
webpack学习-3.管理输出
webpack学习-3.管理输出 1.简单练手2.设置 HtmlWebpackPlugin3.清理 /dist 文件夹4.manifest5.总结 1.简单练手 官网的第一个预先准备,是多入口的。 const path require(path);module.exports {entry: {index: ./src/index.js,print: ./src/print.js,},output: …...

【Go语言反射reflect】
Go语言反射reflect 一、引入 先看官方Doc中Rob Pike给出的关于反射的定义: Reflection in computing is the ability of a program to examine its own structure, particularly through types; it’s a form of metaprogramming. It’s also a great source of …...

LC-1466. 重新规划路线(DFS、BFS)
1466. 重新规划路线 中等 n 座城市,从 0 到 n-1 编号,其间共有 n-1 条路线。因此,要想在两座不同城市之间旅行只有唯一一条路线可供选择(路线网形成一颗树)。去年,交通运输部决定重新规划路线,…...
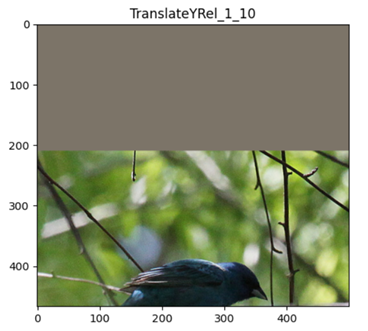
自动数据增广论文笔记 | AutoAugment: Learning Augmentation Strategies from Data
谷歌大脑出品 paper: https://arxiv.org/abs/1805.09501 这里是个论文的阅读心得,笔记,不等同论文全部内容 文章目录 一、摘要1.1 翻译1.2 笔记 二、(第3部分)自动增强:直接在感兴趣的数据集上搜索最佳增强策略2.1 翻译2.2 笔记 三、跳出论文,…...

CTF 7
信息收集 存活主机探测 arp-scan -l 端口探测 nmap -sT --min-rate 10000 -p- 192.168.0.5 服务版本等信息 nmap -sT -sV -sC -O -p22,80,137,138,139,901,5900,8080,10000 192.168.0.5Starting Nmap 7.94 ( https://nmap.org ) at 2023-11-02 21:23 CST Stats: 0:01:30 elaps…...

无公网IP环境Windows系统使用VNC远程连接Deepin桌面
🔥博客主页: 小羊失眠啦. 🎥系列专栏:《C语言》 《数据结构》 《Linux》《Cpolar》 ❤️感谢大家点赞👍收藏⭐评论✍️ 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,…...

java--枚举
1.枚举 枚举是一种特殊类 2.枚举类的格式 注意: ①枚举类中的第一行,只能写一些合法的标识符(名称),多个名称用逗号隔开。 ②这些名称,本质是常量,每个常量都会记住枚举类的一个对象。 3.枚举类的特点 ①枚举类的…...

JVM垃圾回收机制GC
一句话介绍GC: 自动释放不再使用的内存 一、判断对象是否能回收 思路一:引用计数 给这个对象里安排一个计数器, 每次有引用指向它, 就把计数器1, 每次引用被销毁,计数器-1,当计数器为0的时候…...

详解JAVA中的@ApiModel和@ApiModelProperty注解
目录 前言1. ApiModel注解2. ApiModelProperty注解3. 实战 前言 在Java中,ApiModel和ApiModelProperty是Swagger框架(用于API文档的工具)提供的注解,用于增强API文档的生成和展示。这两者搭配使用更佳 使用两者注解,…...
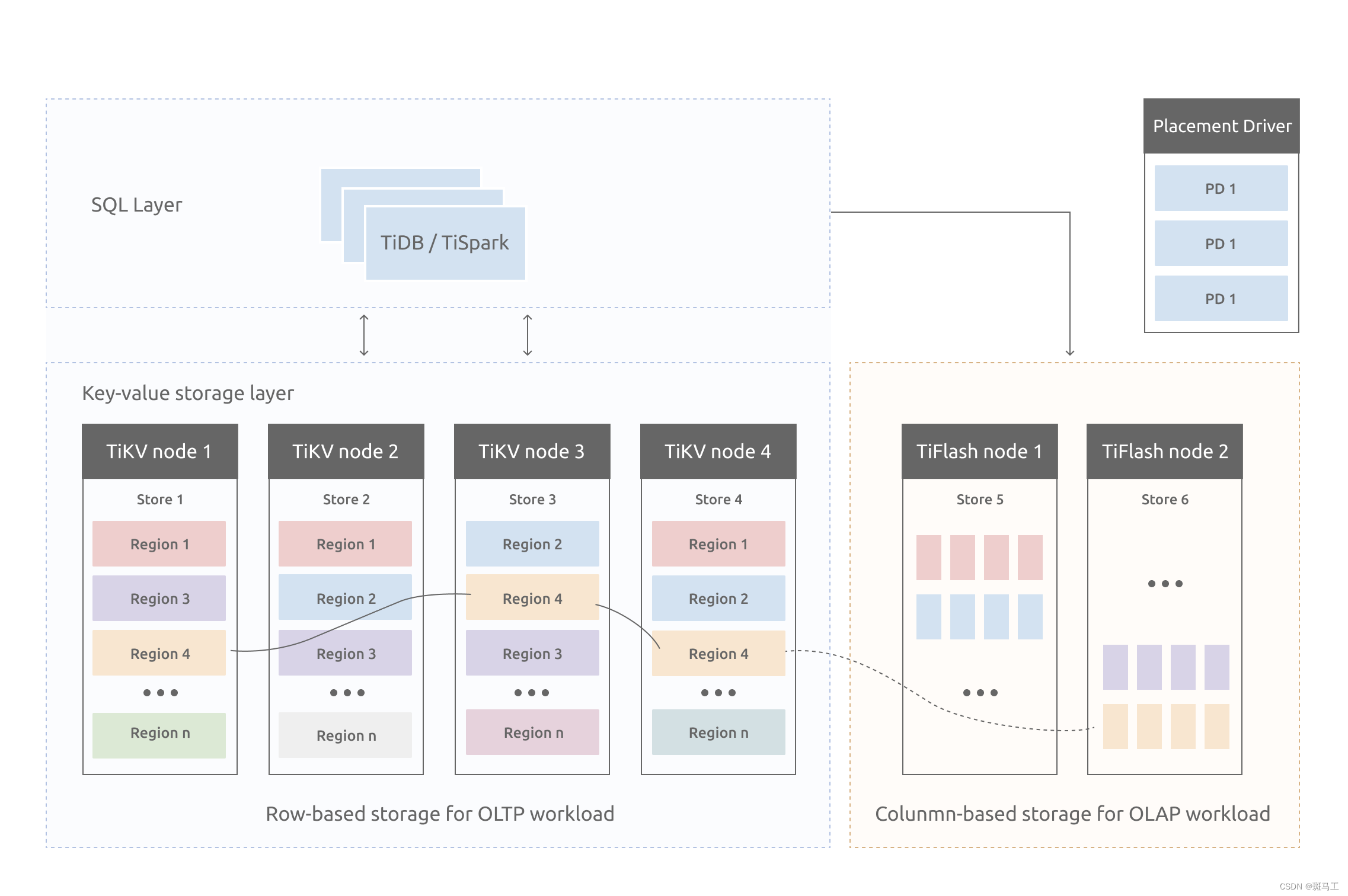
TiDB专题---2、TiDB整体架构和应用场景
上个章节我们讲解了TiDB的发展和特性,这节我们讲下TiDB具体的架构和应用场景。首先我们回顾下TiDB的优势。 TiDB的优势 与传统的单机数据库相比,TiDB 具有以下优势: 纯分布式架构,拥有良好的扩展性,支持弹性的扩缩容…...
性能调优入门
从公众号转载,关注微信公众号掌握更多技术动态 --------------------------------------------------------------- 一、性能定律和数理基础 1.三个定律法则 (1)帕累托法则 我它也被称为 80/20 法则、关键少数法则,或者八二法则。人们在生活中发现很多…...

JavaWeb | 验证码 、 文件的“上传”与“下载”
目录: 验证码 和 文件的“上传”与“下载”1.验证码1.1在JSP上开发验证码 2.“文件上传” 和 “文件下载”2.1“文件上传 ”2.2“文件下载” 验证码 和 文件的“上传”与“下载” 1.验证码 验证码:就是由服务器生成的一串随机数字或符号形成一幅图片&am…...

服务器感染了.halo勒索病毒,如何确保数据文件完整恢复?
导言: 随着科技的不断发展,网络安全问题日益突出,而.halo勒索病毒正是这个数字时代的一大威胁。本文将深入介绍.halo勒索病毒的特点,解释在受到攻击后如何有效恢复被加密的数据文件,并提供一些建议以预防未来可能的威…...
docker安装elasticsearch8.5.0和kibana
服务器环境,centos7 一、安装elasticsearch 1. 创建一个es和kibana通用的网络 docker network create es-net 2. 拉取es镜像,这里选择8.5.0版本 docker pull elasticsearch:8.5.03. 创建挂载目录,并授权 mkdir /usr/local/install/ela…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
