相交链表(LeetCode 160)
文章目录
- 1.问题描述
- 2.难度等级
- 3.热门指数
- 4.解题思路
- 方法一:暴力法
- 方法二:哈希表
- 方法三:双栈
- 方法四:双指针:记录链表长度
- 方法五:双指针:互换遍历
- 5.实现示例
- 参考文献
1.问题描述
给两个单链表的头节点 headA 和 headB ,请找出并返回两个单链表相交的起始节点。如果不存在相交节点,返回 null 。
题目数据保证整个链式结构中不存在环。
注意,函数返回结果后,链表必须保持其原始结构。
示例 1:
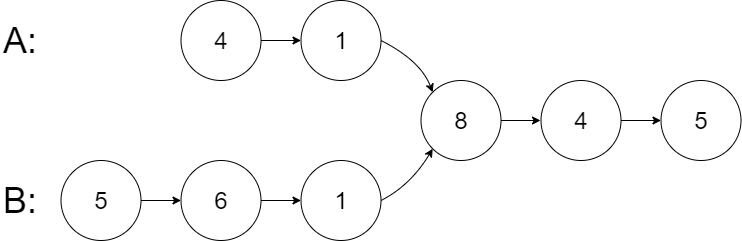
相交返回结点 8。
示例 2:
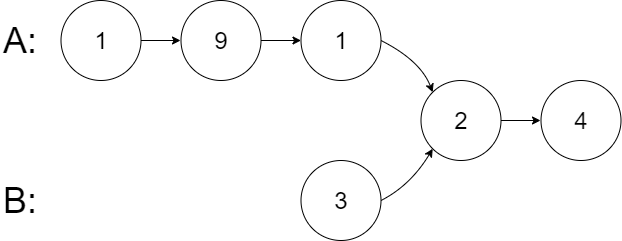
相交返回结点 2。
示例 3:
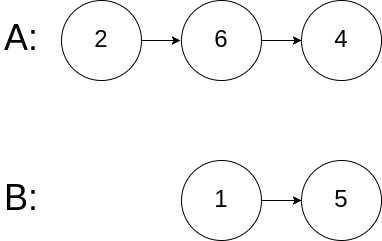
不相交返回 null。
进阶: 你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案?
2.难度等级
Easy。
3.热门指数
★★★★★
出题公司:阿里、腾讯、字节。
4.解题思路
解这道题之前,我们需要首先明确一个概念:何为相交?
相交指的是结点为同一个结点,那么指向结点的指针是相同的,而不是第一个结点值相同。
如果不考虑时间和空间复杂度,那么有多种解法。
假设 m 和 n 是分别是链表 headA 和 headB 的长度。
方法一:暴力法
从头开始遍历第一个链表,遍历第一个链表的每个节点时,同时从头到尾遍历第二个链表,看是否有相同的节点,第一次找到相同的节点即第一个交点。
若第一个链表遍历结束后,还未找到相同的节点,即不存在交点。
时间复杂度: O ( n 2 ) O(n^2) O(n2)。
空间复杂度: O ( 1 ) O(1) O(1)。
方法二:哈希表
判断两个链表是否相交,可以使用哈希集合存储链表节点。
首先遍历链表 headA,将链表中的每个节点加入哈希表中。然后遍历链表 headB,判断节点是否在哈希表中。
如果链表 headB 中的所有节点都不在哈希集合中,则两个链表不相交,返回 null。
时间复杂度: O(m+n),需要遍历两个链表各一次。
空间复杂度: O(m),需要使用哈希表存储链表 headA 的全部节点。
方法三:双栈
我们可以从头遍历两个链表。创建两个栈,第一个栈存储第一个链表的节点,第二个栈存储第二个链表的节点。每遍历到一个节点时,就将该节点入栈。两个链表都入栈结束后。
则通过判断栈顶的节点是否相等即可判断两个单链表是否相交。因为我们知道,若两个链表相交,则从第一个相交节点开始,后面的节点都相交。
若两链表相交,则循环出栈,直到遇到两个出栈的节点不相同,则这个节点的后一个节点就是第一个相交的节点。
时间复杂度: O(m+n)。需要遍历两个链表各两次,一次是入栈,一次是出栈。
空间复杂度: O(m+n),需要使用两个栈存储链表 headA 和 headB 的所有结点。
方法四:双指针:记录链表长度
同时遍历两个链表到尾部,同时记录两个链表的长度。若两个链表最后的一个节点相同,则两个链表相交。
有两个链表的长度后,我们就可以知道哪个链表长,设较长的链表长度为 len1,短的链表长度为 len2。
则先让较长的链表向后移动 len1-len2 个长度。然后开始从当前位置同时遍历两个链表,当遍历到的链表的节点相同时,则这个节点就是第一个相交的节点。
时间复杂度: O ( m + n ) O(m+n) O(m+n),两个指针同时遍历两个链表,然后再遍历两个链表至相同结点。
空间复杂度: O ( 1 ) O(1) O(1)。
方法五:双指针:互换遍历
当链表 headA 和 headB 都不为空时,创建两个指针 pA 和 pB,初始时分别指向两个链表的头节点 headA 和 headB,然后将两个指针依次遍历两个链表的每个节点。具体做法如下:
-
每步操作需要同时更新指针 pA 和 pB。
-
如果指针 pA 不为空,则将指针 pA 移到下一个节点;如果指针 pB 不为空,则将指针 pB 移到下一个节点。
-
如果指针 pA 为空,则将指针 pA 移到链表 headB 的头节点;如果指针 pB 为空,则将指针 pB 移到链表 headA 的头节点。
-
当指针 pA 和 pB 指向同一个节点或者都为空时,返回它们指向的节点或者 null。
为什么第一次遍历完后互换从头遍历后,如果相交会同时到达相交结点呢?
假设下面是一个相交的两个链表,省去了结点。其中链表 headA 的长度为 a + c = m,链表 headB 的长度为 b + c = n。
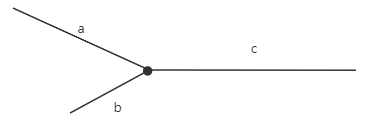
因为 a + c + b 等于 b + c + a,所以第一次遍历完后互换从头遍历,会同时到达相交结点。
如果两个链表不相交,也会同时到达尾结点,因为 m + n 等于 n + m。
时间复杂度: O ( m + n ) O(m+n) O(m+n),两个指针同时遍历两个链表,然后再遍历两个链表至相同结点。
空间复杂度: O ( 1 ) O(1) O(1)。
5.实现示例
面以 Golang 为例,给出「双指针:互换遍历」的实现。
/*** Definition for singly-linked list.* type ListNode struct {* Val int* Next *ListNode* }*/
func getIntersectionNode(headA, headB *ListNode) *ListNode {pA, pB := headA, headBfor pA != nil || pB != nil {if pA == pB {return pA}if pA == nil {pA = headB} else {pA = pA.Next}if pB == nil {pB = headA} else {pB = pB.Next} }return nil
}
参考文献
160. 相交链表 - LeetCode
判断两个单链表是否相交及找到第一个交点原创 -CSDN
相关文章:

相交链表(LeetCode 160)
文章目录 1.问题描述2.难度等级3.热门指数4.解题思路方法一:暴力法方法二:哈希表方法三:双栈方法四:双指针:记录链表长度方法五:双指针:互换遍历 5.实现示例参考文献 1.问题描述 给两个单链表的…...
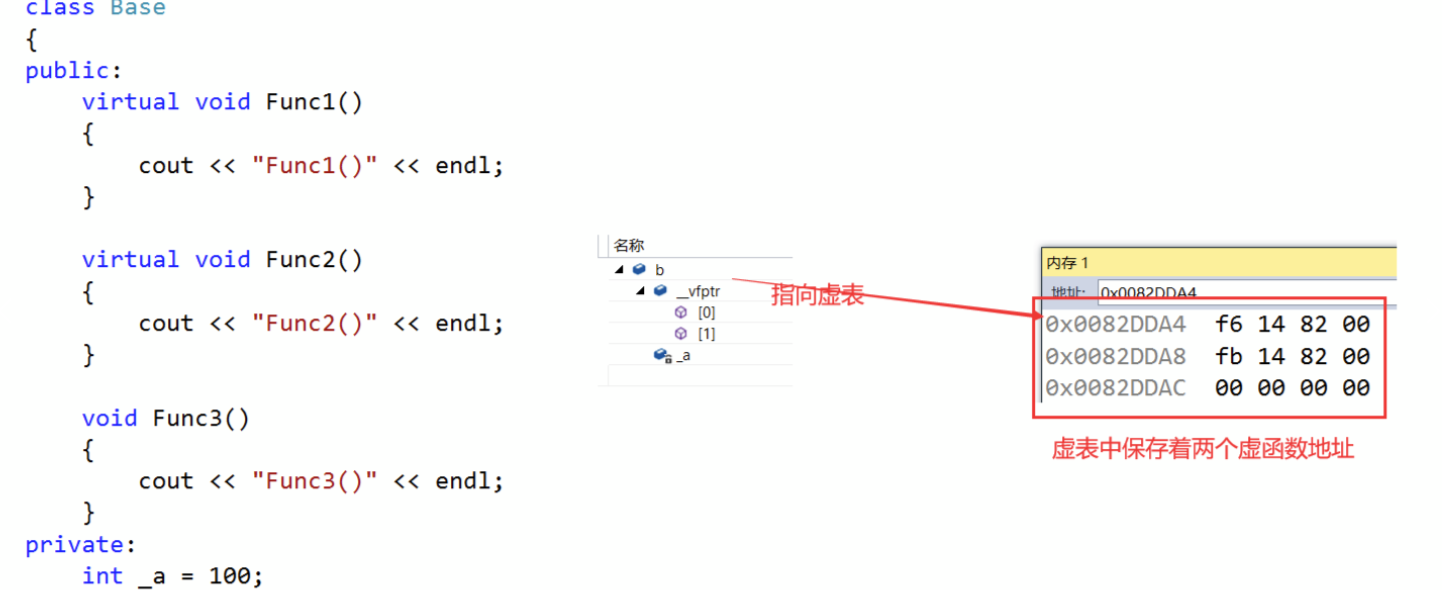
C++多态(详解)
一、多态的概念 1.1、多态的概念 多态:多种形态,具体点就是去完成某个行为,当不同的对象去完成时会产生出不同的状态。 举个例子:比如买票这个行为,当普通人买票时,是全价买票;学生买票时&am…...
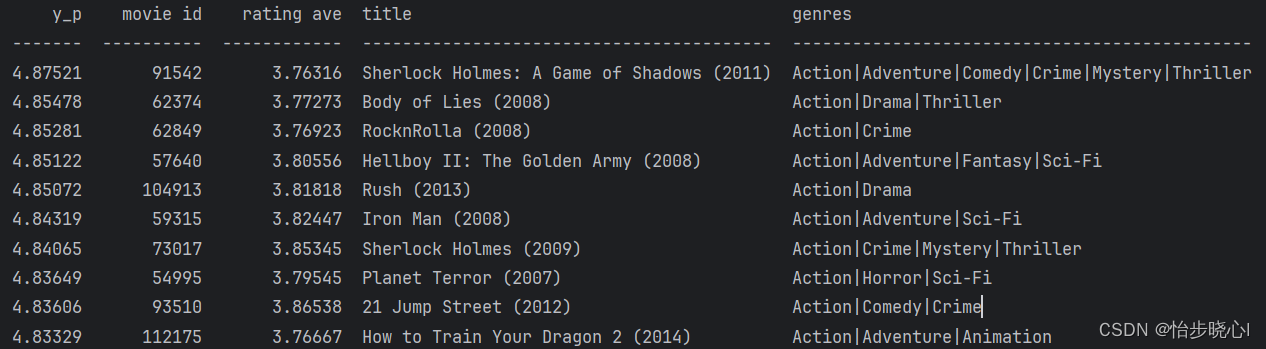
06、基于内容的过滤算法Tensorflow实现
06、基于内容的过滤算法Tensorflow实现 开始学习机器学习啦,已经把吴恩达的课全部刷完了,现在开始熟悉一下复现代码。全部工程可从最上方链接下载。 05、基于梯度下降的协同过滤算法中已经介绍了协同过滤算法的基本实现方法,但是这种方法仅…...
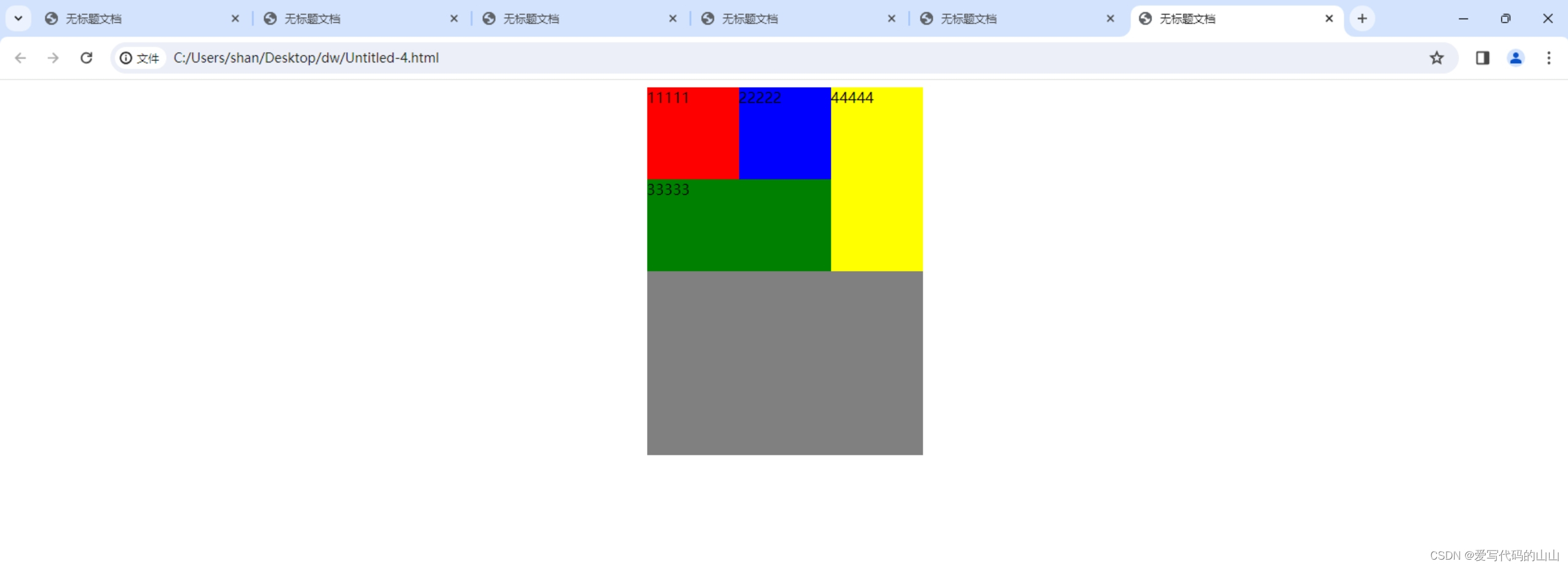
html/css中用float实现的盒子案例
运行效果: 代码部分: <!doctype html> <html> <head> <meta charset"utf-8"> <title>无标题文档</title> <style type"text/css">.father{width:300px; height:400px; background:gray;…...
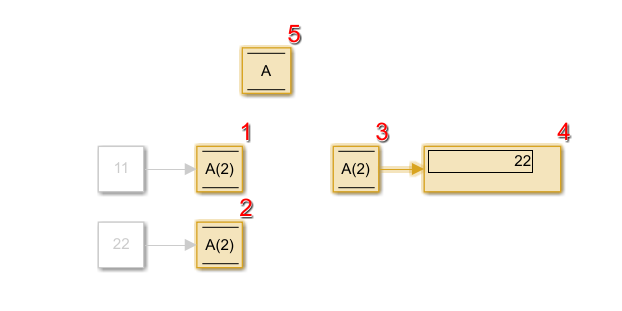
simulink中 Data store memory、write和read模块及案例介绍
目录 1.Data store memory模块 2.data store write模块 3.data store read模块 4.仿真分析 4.1简单使用三个模块 4.2 模块间的调用顺序剖析 1.Data store memory模块 向右拖拉得到Data store read模块,向左拉得到Data write模块 理解:可视为定义变量…...
java设计模式学习之【装饰器模式】
文章目录 引言装饰器模式简介定义与用途实现方式 使用场景优势与劣势装饰器模式在Spring中的应用画图示例代码地址 引言 在日常生活中,我们常常对基本事物添加额外的装饰以增强其功能或美观。例如,给手机加一个保护壳来提升其防护能力,或者在…...
Ubuntu宝塔面板本地部署Emlog个人博客网站并远程访问【内网穿透】
文章目录 前言1. 网站搭建1.1 Emolog网页下载和安装1.2 网页测试1.3 cpolar的安装和注册 2. 本地网页发布2.1 Cpolar临时数据隧道2.2.Cpolar稳定隧道(云端设置)2.3.Cpolar稳定隧道(本地设置) 3. 公网访问测试总结 前言 博客作为使…...

简述IO流的使用以及使用时需要注意的事项
Hi i,m JinXiang ⭐ 前言 ⭐ 本篇文章主要介绍介绍IO流的使用以及使用时需要注意的事项以及部分理论知识 🍉欢迎点赞 👍 收藏 ⭐留言评论 📝私信必回哟😁 🍉博主收将持续更新学习记录获,友友们有任何问题可…...
西工大计算机学院计算机系统基础实验一(函数编写11~14)
稳住心态不要慌,如果考试周冲突的话,可以直接复制这篇博客和上一篇博客西工大计算机学院计算机系统基础实验一(函数编写1~10)-CSDN博客最后的代码,然后直接提交,等熬过考试周之后回过头再慢慢做也可以。 第…...
Spring 声明式事务
Spring 声明式事务 1.Spring 事务管理概述1.1 事务管理的重要性1.2 Spring事务管理的两种方式1.2.1 编程式事务管理1.2.2 声明式事务管理 1.3 为什么选择声明式事务管理 2. 声明式事务管理2.1 基本用法2.2 常用属性2.2.1 propagation(传播行为)2.2.2 iso…...

通达OA inc/package/down.php接口存在未授权访问漏洞
声明 本文仅用于技术交流,请勿用于非法用途 由于传播、利用此文所提供的信息而造成的任何直接或者间接的后果及损失,均由使用者本人负责,文章作者不为此承担任何责任。 一. 产品简介 通达OA(Office Anywhere网络智能办公系统&am…...

数据库原理: 笛卡儿积
笛卡儿积(Cartesian Product)是集合论中的一个概念,也在数据库中的查询操作中经常使用。笛卡儿积是指两个集合(或更多集合)之间所有可能的组合。如果有两个集合A和B,它们的笛卡儿积记作A B,表示…...
docker安装配置prometheus+node_export+grafana
简介 Prometheus是一套开源的监控预警时间序列数据库的组合,Prometheus本身不具备收集监控数据功能,通过获取不同的export收集的数据,存储到时序数据库中。Grafana是一个跨平台的开源的分析和可视化工具,将采集过来的数据实现可视…...
【JavaScript】JS——Map数据类型
【JavaScript】JS——Map数据类型 什么是Map?特性Map与Object的比较 map的创建map的属性map相关方法map的遍历 什么是Map? 存储键值对的对象。 能够记住键的原始插入顺序任何值(对象或原始值)都可以作为键或值。 特性 Map中的一个键只能出现一次&am…...
【【FPGA的 MicroBlaze 的 介绍与使用 】】
FPGA的 MicroBlaze 的 介绍与使用 可编程片上系统(SOPC)的设计 在进行系统设计时,倘若系统非常复杂,采用传统 FPGA 单独用 Verilog/VHDL 语言进行开发的方式,工作量无疑是巨大的,这时调用 MicroBlaze 软核…...

PyQt pdf格式保存
参考文章 pyqt5:利用QFileDialog从本地选择图片\文本文档显示到label、保存图片\label文本到本地(附代码)_pyqt5中qfiledialog.getopenfileurl-CSDN博客 txt文件的打开与保存 def openTextFile(self): # 选择文本文件上传fd,fp QFileDialog.getOpen…...

微前端介绍
目录 微前端概念 微前端特性 场景演示 微前端方案 iframe 方案 qiankun 方案 micro-app 方案 EMP 方案 无界微前端 方案 无界方案 成本低 速度快 原生隔离 功能强大 总结 前言:微前端已经是一个非常成熟的领域了,但开发者不管采用哪个现…...
使用说明书(一,轻量级的visionpro))
工业机器视觉megauging(向光有光)使用说明书(一,轻量级的visionpro)
机器视觉megauging(未名之光,向光有光)程序软件资源已经发布,欢迎下载尝新 8:11 2023/12/2 首先,既然觉得可以发表了,就发表。 其次,我这个人没写过什么软件使用说明书,既然走到这路…...

Java——面试:String 和 StringBuffer 的区别?
相同点: String 和 StringBuffer,它们可以储存和操作字符串, 即包含多个字符的字符数据。 String 和 StringBuffer 的区别有以下几点: 1.String 类提供了数值不可改变的字符串。而 StringBuffer 类提供的字符串进行修改。 当你知…...

图扑软件受邀出席高交会-全球清洁能源创新博览会
“相聚鹏城深圳,共享能源盛宴” 第二十五届中国国际高新技术成果交易会(简称“高交会”)于 11 月 15-18 日在深圳盛大开幕。高交会由商务部、科学技术部、工业和信息化部、国家发展改革委、农业农村部、国家知识产权局、中国科学院、中国工程院和深圳市人民政府共同…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
