西工大计算机学院计算机系统基础实验一(函数编写11~14)
稳住心态不要慌,如果考试周冲突的话,可以直接复制这篇博客和上一篇博客西工大计算机学院计算机系统基础实验一(函数编写1~10)-CSDN博客最后的代码,然后直接提交,等熬过考试周之后回过头再慢慢做也可以。
第11个函数,rempwr2,要求计算x%(2^n),其中0<=n<=30。比如rempwr2(15,2) = 3, rempwr2(-35,3) = -3。什么意思呢?意思是15%(2^2)=15%4=3,-35%(2^3)=-35%8=-3。那么我们该怎么做呢?先考虑正数,当x为15并且n为2时,15可写作1111B,15%(2^2)即相当于取1111B的低2个比特位,即11B,正如答案中的3。接着考虑负数,-35可写作0xFFFF FFFF FFFF FFDD,-3可写作0xFFFF FFFF FFFF FFFD,如果像处理正数那样直接截取0xFFFF FFFF FFFF FFDD的第3个比特位的话,得到的应该是101B,也就是5,而不是-3,所以负数不能像正数那样被处理。最简单的方法是分类讨论,但是那样会使用蛮多的运算符,所以尝试使用一种新的思路去处理这个问题。我们可不可以这样子,先计算35%(2^3)=3,然后再把3变为-3呢?也就是说,先把一个数变成它自己的绝对值,然后参与%运算,最后再根据最开始这个数的符号位调整最终的结果呢?按照这个思路,我们首先将x变成它的绝对值,可以通过(x+(x>>31))^(x>>31)来实现,当为正时,(x+(x>>31))^(x>>31)的结果仍为x,当x为负数时,比如x=-35=0xFFFF FFDD,那么x>>31=0xFFFF FFFF,x+(x>>31)的结果是0xFFFF FFDE,接着0xFFFF FFDE与0xFFFF FFFF异或,得到了0x0000 0023,也就是35。(当x为负数时,+(x>>31)相当于-1,接着与x>>31异或相当于全取反,就是根据负数原码求补码的逆过程,只不过考虑到表达式(x+(x>>31))^(x>>31)也综合了x是正数的情况,所以不方便直白的写减一后全取反)接着当n=2时如何产生0000... ...0011,当n=3时如何产生0000... ...0111呢?可以通过(~0)+(1<<n)来产生。~0为0xFFFF FFFF,当n=3时,1<<3为0x8,~0+(1<<3)即得到了0x0000 0007。这时让((x+(x>>31))^(x>>31))与~0+(1<<n)进行位与操作,即可完成%操作。此时若x是正数,则所有步骤已完成,但是当x为负数时,还需要将最后的结果加一个负号。怎么加负号呢?各位取反加1,先与x>>31做异或操作完成各位取反,最后减去x>>31完成加1。结合上述的讲解,我们给出代码,如 图1:编写第11个函数rempwr2 所示。接着仿照前10个函数相同的检查流程,如 图2:检查第11个函数rempwr2 所示。
int s = x>>31;
x = (x+s)^s;
x &= ((~0)+(1<<n));
return (x^s)+~s+1;(图1:编写第11个函数rempwr2)


(图2:检查第11个函数rempwr2)
第12个函数,satMul2,执行算术乘法乘2。怎么做呢?如果x为小于0x4000 0000的正数,或者为0,或者为大于C000 0000的负数,那么直接返回x<<1即可。而当x超出这个范围时,就不能直接返回x<<1了。那如何判断什么时候可以直接返回x<<1,什么时候不能直接返回x<<1呢?发现可以引入变量int x2=x<<1,x2表示x*2,再引入变量int sx2=(x2)>>31表示x*2的符号位,一旦x的符号位与x<<1的符号位不相同,即(x^x2)>>31的结果为0xFFFF FFFF时,就不能直接返回x<<1,而如果x的符号位与x<<1的符号位相同,即(x^x2)>>31的结果为0x0时,就可以直接返回x<<1,所以可以引入变量int flag=(x^x2)>>31,并以此作为判断条件。根据已有的知识,可以写出下面的大框架:
(flag&( )) | (~flag&( x2 ))
接着,如果x的符号位与x<<1的符号位不相同,即(x^x2)>>31的结果为0xFFFF FFFF,不能直接返回x<<1时,该返回什么呢?易知此时只需返回0x8000 0000或者0x7FFF FFFF。该如何得知该返回0x8000 0000还是该返回0x7FFF FFFF呢?发现这时当x为很大的正数,并且x2的符号位为1时,sx2为0xFFFF FFFF,加上0x8000 0000之后即为0x7FFF FFFF,即应该返回的值;当x为很小的负数,并且x2的符号位为0时,sx2为0x0000 0000,加上0x8000 0000之后即为0x8000 0000,即应该返回的值。而0x8000 0000可写作1<<31。根据这个分析,我们进一步完善大框架:
(flag&( sx2+(1<<31) )) | (~flag&( x2 ))
这时再思考,能不能想办法进行优化以减少运算符使用的个数呢?发现当flag为0xFFFF FFFF时,(~flag&( x2 )中的x2不一定一定为0;当~flag为0xFFFF FFFF时,(flag&( sx2+(1<<31) ))中的sx2+(1<<31)也不一定一定为0,所以不能像第9个函数那样进行优化。因此,第12题最终的代码为如 图3:编写第12个函数satMul2 所示。
int x2=x<<1;int sx2=x2>>31;int flag=(x^x2)>>31;int tmin=1<<31;return ((~flag&x2)+(flag&(sx2+tmin)));(图3:编写第12个函数satMul2)
然而这道题似乎有问题。为什么呢?其实只要简单的"return x<<1"就能通过!白白耗费我们这么多时间。如 图4:检查第12个函数satMul2 所示。

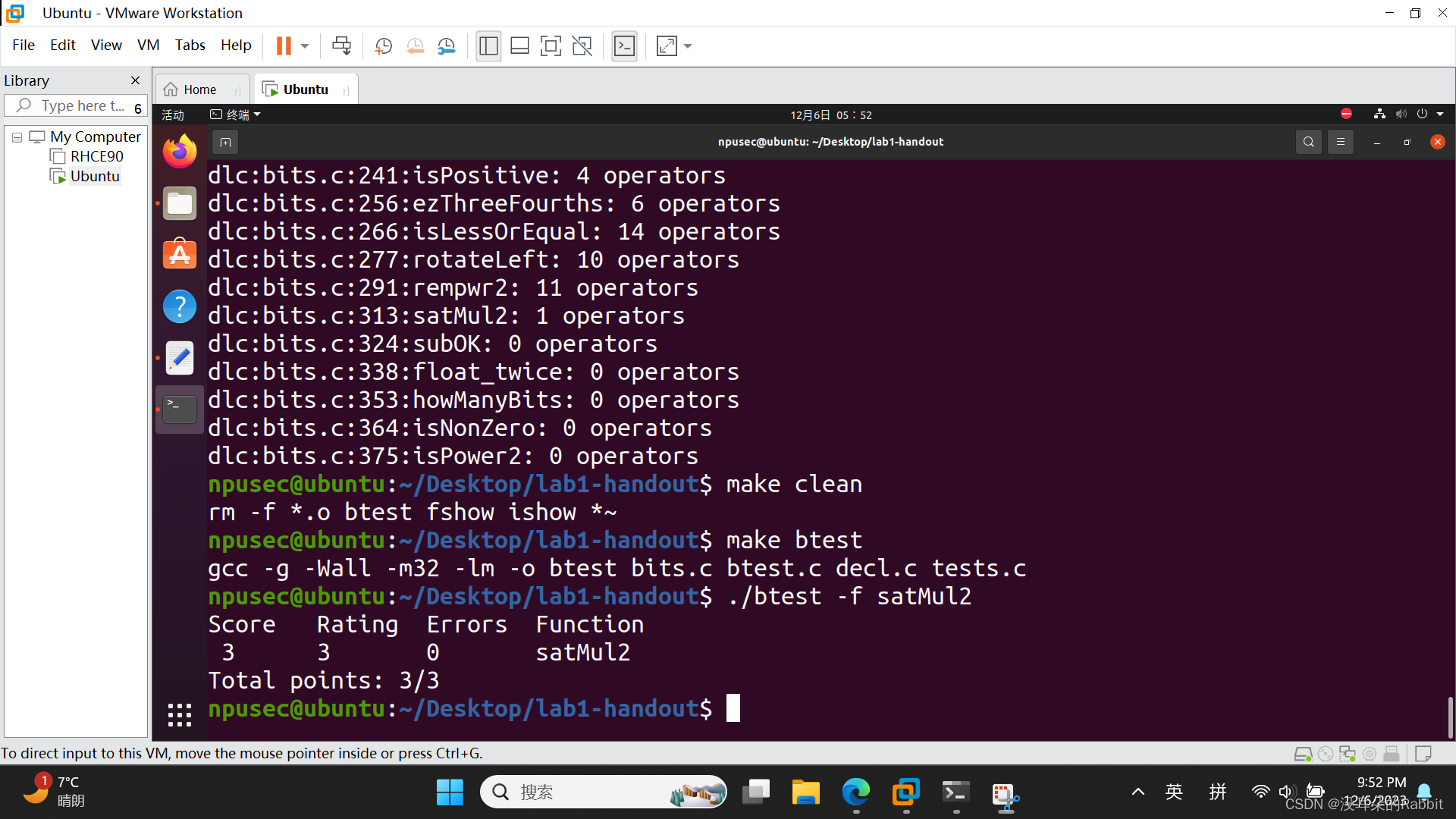
(图4:检查第12个函数satMul2)
第13个函数,subOK,如果x减去y的值能被int类型大小的变量装得下,就返回1,否则返回0。接着我们发现,当x与y同号时,不可能出现装不下也就是溢出的问题,只有当x与y异号时,才可能会用装不下也就是溢出的问题,顺着这个思路,我们可以分成两类来讨论。而分类的依据则是x^~y,当x与y同号时,x^~y的符号位为1,当x与y异号时,x^~y的符号位为0。顺着这个思路,写出下面的大框架:
(( (x^~y)&( ) | ( ~(x^~y)&( ) ) ) >>31)&1
当x与y同号时,x与~y异号,x^~y的符号位为1,此时x减去y的值一定能被int类型大小的变量装得下,所以此时返回1即可。这时大框架即为:
(( (x^~y) | ( ~(x^~y)&( ) ) ) >>31)&1
而当x与y异号时,x与~y同号,x^~y的符号位为0,此时如果x与x-y=x+~y+1异号,那么必定发生了溢出,x减去y的值一定不能被int类型大小的变量装得下,所以选择表达式~(x^(x+~y+1)),当x与x-y同号时,说明可以装得下,应该返回1,而~(x^(x+~y+1))的符号位恰好就是1;当当x与x-y异号时,说明不可以装得下,应该返回0,而~(x^(x+~y+1))的符号位恰好就是0。所以最终的大框架即为:
(( (x^~y) | ( ~(x^~y)&( ~(x^(x+~y+1)) ) ) ) >>31)&1
代码如 图5:编写第13个函数subOK 所示。检查过程如 图6:检查第13个函数subOK 所示。
int flag=x^~y;return ((flag|(~flag&(~(x^(x+~y+1)))))>>31)&1;(图5:编写第13个函数subOK)
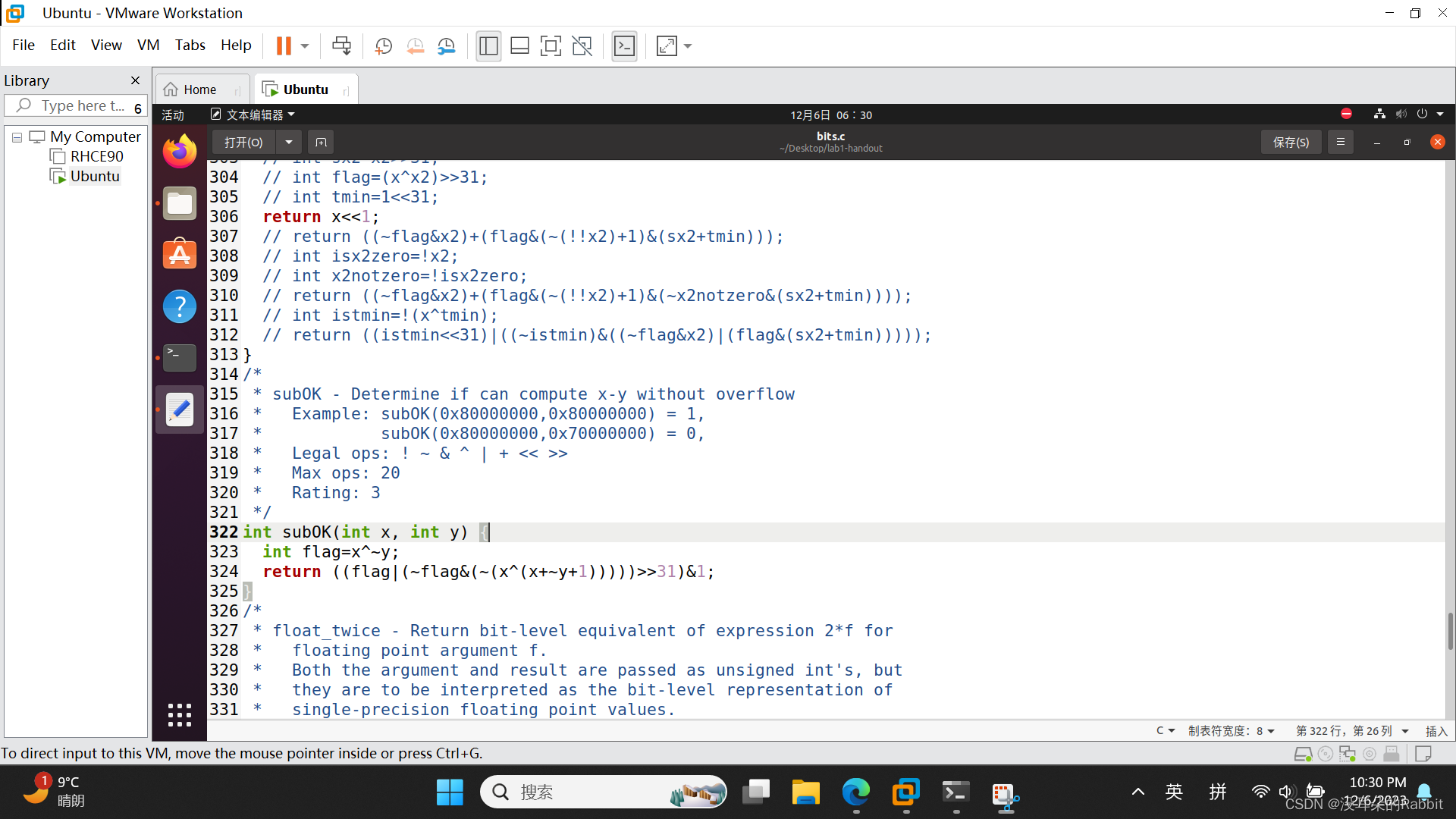
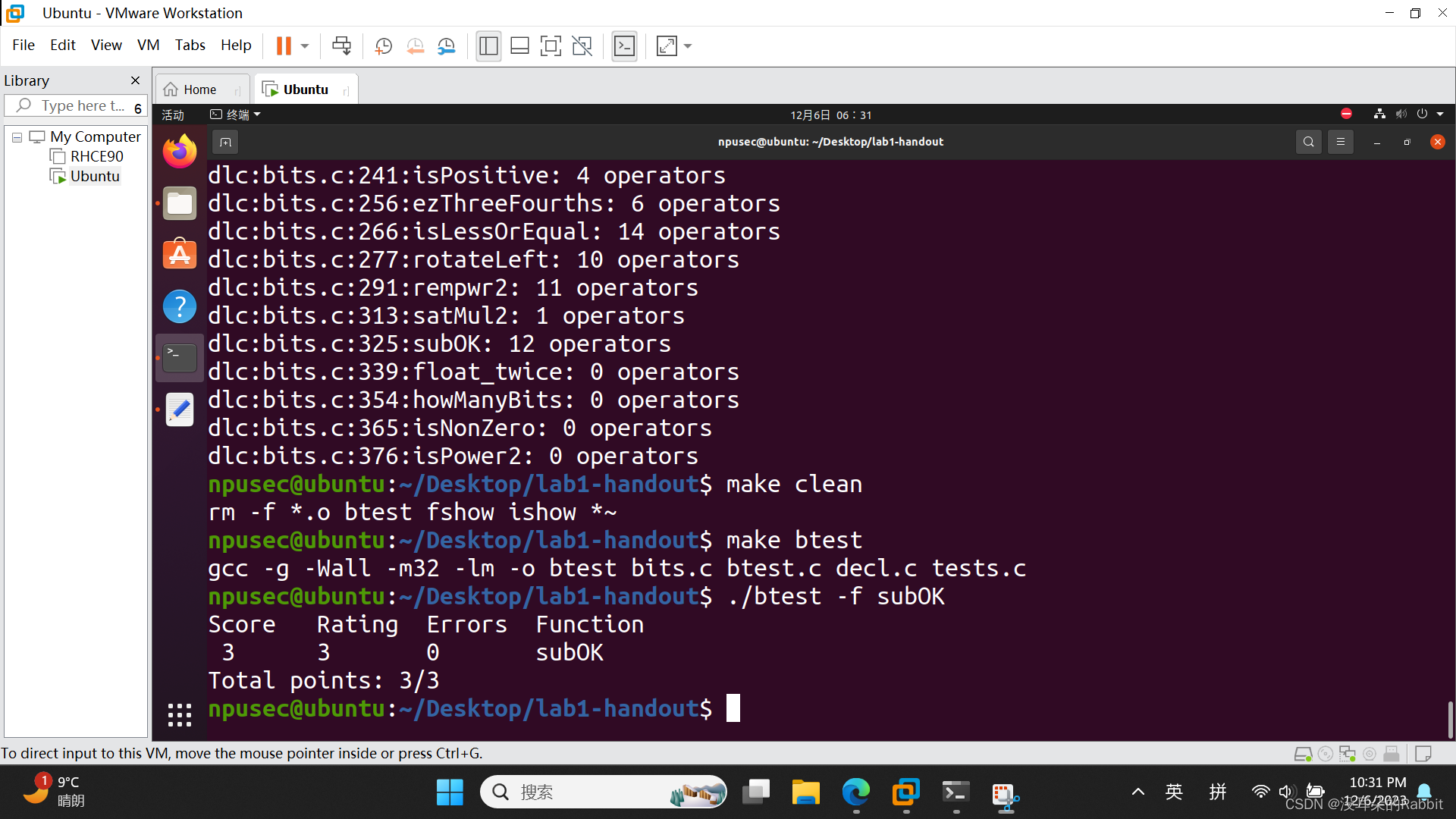
(图6:检查第13个函数subOK)
第14个函数,float_twice,在这里限制被释放,条件判断可以被使用,while语句也可以被使用,||和&&也可以被使用,而且也可以创建unsigned型的局部变量。那么这个函数要求我们做到什么呢?这个函数要求我们,对于一个浮点数f,计算2*f。举个例子来讲,如果f=0.625,那么其在计算机内部的表示形式为0x3F20 0000,计算2*f可以得到0x3FA0 0000,而这个0x3FA0 0000就是期待我们返回的值。对不起大家,在这里作者实在有点累了,所以没办法今天就讲完了。代码如 图7:编写第14个函数float_twice 所示。检查第14个函数的过程如 图8:检查第14个函数float_twice 所示
unsigned sign = 0, enow = 0, fnow = 0;unsigned pos = 1 << 31;unsigned frule = (1 << 23) - 1;if (uf == 0) {return 0;}if (uf == pos) {return uf;}sign = uf & pos;enow = (uf >> 23) & 0xff;if (enow == 0xff) {return uf;}fnow = uf & frule;if (enow == 0) {fnow = fnow << 1;if (fnow & (1 << 23)) {fnow = fnow & frule;enow += 1;}}else{enow += 1;}return sign | (enow << 23) | fnow;(图7:编写第14个函数float_twice)
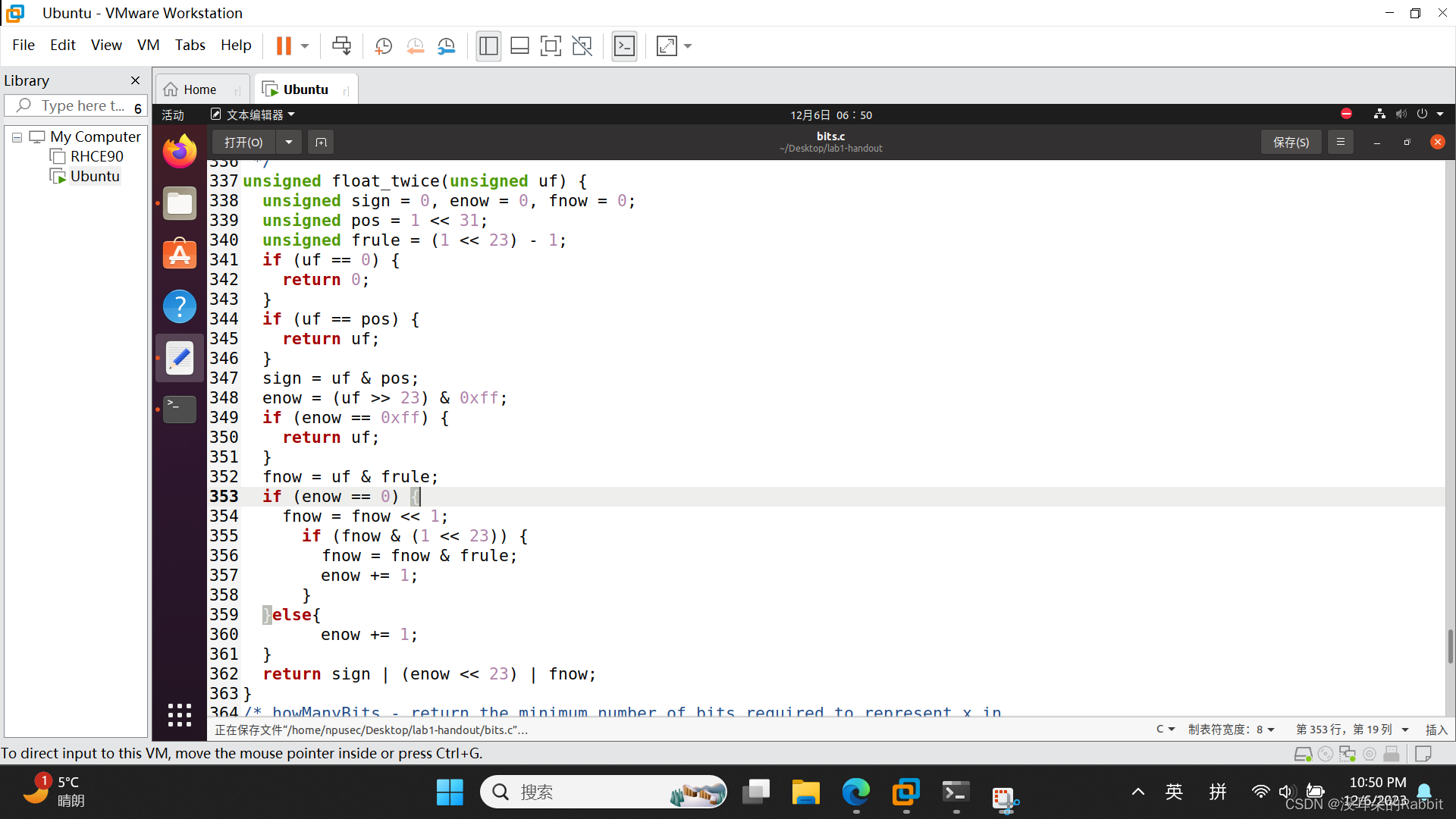
(图8:检查第14个函数float_twice)
/* * rempwr2 - Compute x%(2^n), for 0 <= n <= 30* Negative arguments should yield negative remainders* Examples: rempwr2(15,2) = 3, rempwr2(-35,3) = -3* Legal ops: ! ~ & ^ | + << >>* Max ops: 20* Rating: 3*/
int rempwr2(int x, int n) {int s = x>>31;x = (x+s)^s;x &= ((~0)+(1<<n));return (x^s)+~s+1;
}
/** satMul2 - multiplies by 2, saturating to Tmin or Tmax if overflow* Examples: satMul2(0x30000000) = 0x60000000* satMul2(0x40000000) = 0x7FFFFFFF (saturate to TMax)* satMul2(0x80034000) = 0x80000000 (saturate to TMin)* Legal ops: ! ~ & ^ | + << >>* Max ops: 20* Rating: 3*/
int satMul2(int x) {// int x2=x<<1;// int sx2=x2>>31;// int flag=(x^x2)>>31;// int tmin=1<<31;return x<<1;// return ((~flag&x2)+(flag&(~(!!x2)+1)&(sx2+tmin)));// int isx2zero=!x2;// int x2notzero=!isx2zero;// return ((~flag&x2)+(flag&(~(!!x2)+1)&(~x2notzero&(sx2+tmin))));// int istmin=!(x^tmin);// return ((istmin<<31)|((~istmin)&((~flag&x2)|(flag&(sx2+tmin)))));
}
/* * subOK - Determine if can compute x-y without overflow* Example: subOK(0x80000000,0x80000000) = 1,* subOK(0x80000000,0x70000000) = 0, * Legal ops: ! ~ & ^ | + << >>* Max ops: 20* Rating: 3*/
int subOK(int x, int y) {int flag=x^~y;return ((flag|(~flag&(~(x^(x+~y+1)))))>>31)&1;
}
/* * float_twice - Return bit-level equivalent of expression 2*f for* floating point argument f.* Both the argument and result are passed as unsigned int's, but* they are to be interpreted as the bit-level representation of* single-precision floating point values.* When argument is NaN, return argument* Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while* Max ops: 30* Rating: 4*/
unsigned float_twice(unsigned uf) {unsigned sign = 0, enow = 0, fnow = 0;unsigned pos = 1 << 31;unsigned frule = (1 << 23) - 1;if (uf == 0) {return 0;}if (uf == pos) {return uf;}sign = uf & pos;enow = (uf >> 23) & 0xff;if (enow == 0xff) {return uf;}fnow = uf & frule;if (enow == 0) {fnow = fnow << 1;if (fnow & (1 << 23)) {fnow = fnow & frule;enow += 1;}}else{enow += 1;}return sign | (enow << 23) | fnow;
}相关文章:

西工大计算机学院计算机系统基础实验一(函数编写11~14)
稳住心态不要慌,如果考试周冲突的话,可以直接复制这篇博客和上一篇博客西工大计算机学院计算机系统基础实验一(函数编写1~10)-CSDN博客最后的代码,然后直接提交,等熬过考试周之后回过头再慢慢做也可以。 第…...
Spring 声明式事务
Spring 声明式事务 1.Spring 事务管理概述1.1 事务管理的重要性1.2 Spring事务管理的两种方式1.2.1 编程式事务管理1.2.2 声明式事务管理 1.3 为什么选择声明式事务管理 2. 声明式事务管理2.1 基本用法2.2 常用属性2.2.1 propagation(传播行为)2.2.2 iso…...

通达OA inc/package/down.php接口存在未授权访问漏洞
声明 本文仅用于技术交流,请勿用于非法用途 由于传播、利用此文所提供的信息而造成的任何直接或者间接的后果及损失,均由使用者本人负责,文章作者不为此承担任何责任。 一. 产品简介 通达OA(Office Anywhere网络智能办公系统&am…...

数据库原理: 笛卡儿积
笛卡儿积(Cartesian Product)是集合论中的一个概念,也在数据库中的查询操作中经常使用。笛卡儿积是指两个集合(或更多集合)之间所有可能的组合。如果有两个集合A和B,它们的笛卡儿积记作A B,表示…...
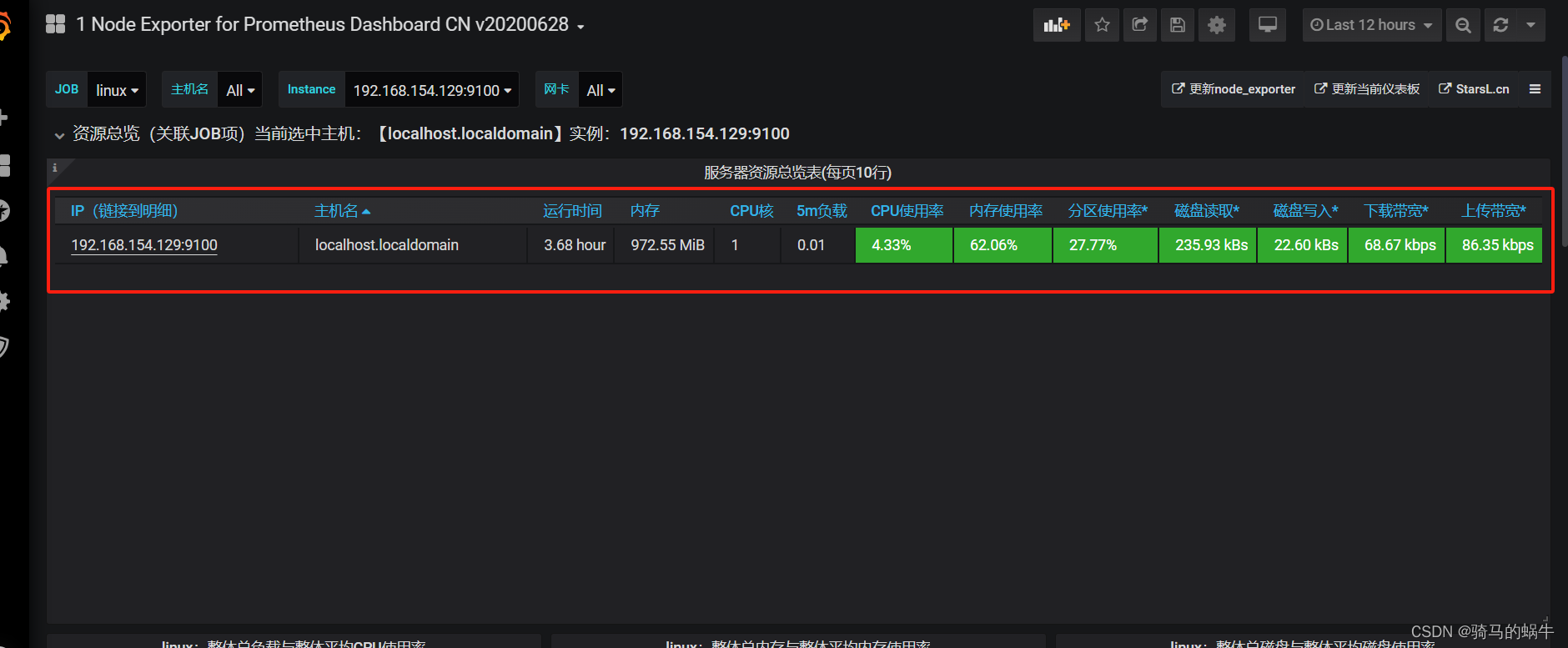
docker安装配置prometheus+node_export+grafana
简介 Prometheus是一套开源的监控预警时间序列数据库的组合,Prometheus本身不具备收集监控数据功能,通过获取不同的export收集的数据,存储到时序数据库中。Grafana是一个跨平台的开源的分析和可视化工具,将采集过来的数据实现可视…...
【JavaScript】JS——Map数据类型
【JavaScript】JS——Map数据类型 什么是Map?特性Map与Object的比较 map的创建map的属性map相关方法map的遍历 什么是Map? 存储键值对的对象。 能够记住键的原始插入顺序任何值(对象或原始值)都可以作为键或值。 特性 Map中的一个键只能出现一次&am…...
【【FPGA的 MicroBlaze 的 介绍与使用 】】
FPGA的 MicroBlaze 的 介绍与使用 可编程片上系统(SOPC)的设计 在进行系统设计时,倘若系统非常复杂,采用传统 FPGA 单独用 Verilog/VHDL 语言进行开发的方式,工作量无疑是巨大的,这时调用 MicroBlaze 软核…...

PyQt pdf格式保存
参考文章 pyqt5:利用QFileDialog从本地选择图片\文本文档显示到label、保存图片\label文本到本地(附代码)_pyqt5中qfiledialog.getopenfileurl-CSDN博客 txt文件的打开与保存 def openTextFile(self): # 选择文本文件上传fd,fp QFileDialog.getOpen…...

微前端介绍
目录 微前端概念 微前端特性 场景演示 微前端方案 iframe 方案 qiankun 方案 micro-app 方案 EMP 方案 无界微前端 方案 无界方案 成本低 速度快 原生隔离 功能强大 总结 前言:微前端已经是一个非常成熟的领域了,但开发者不管采用哪个现…...
使用说明书(一,轻量级的visionpro))
工业机器视觉megauging(向光有光)使用说明书(一,轻量级的visionpro)
机器视觉megauging(未名之光,向光有光)程序软件资源已经发布,欢迎下载尝新 8:11 2023/12/2 首先,既然觉得可以发表了,就发表。 其次,我这个人没写过什么软件使用说明书,既然走到这路…...

Java——面试:String 和 StringBuffer 的区别?
相同点: String 和 StringBuffer,它们可以储存和操作字符串, 即包含多个字符的字符数据。 String 和 StringBuffer 的区别有以下几点: 1.String 类提供了数值不可改变的字符串。而 StringBuffer 类提供的字符串进行修改。 当你知…...

图扑软件受邀出席高交会-全球清洁能源创新博览会
“相聚鹏城深圳,共享能源盛宴” 第二十五届中国国际高新技术成果交易会(简称“高交会”)于 11 月 15-18 日在深圳盛大开幕。高交会由商务部、科学技术部、工业和信息化部、国家发展改革委、农业农村部、国家知识产权局、中国科学院、中国工程院和深圳市人民政府共同…...
vue项目下npm或yarn下安装echarts多个版本
最近在大屏展示的时候,用到了百度的echarts图表库,看完效果图后,又浏览了一下echarts官网案例,大同小异。但是搬砖过程中发现实际效果和demo相差甚远,一番折腾发现,项目中安装的是echarts4.x版本࿰…...

在内网开发中使用Nginx代理来访问钉钉新版服务端API
如果你在内网开发中使用Nginx代理来访问钉钉新版服务端API,你可以在Nginx配置文件中进行相应的配置。 以下是一个简单的示例Nginx配置,用于将对指定URL的请求代理到钉钉服务端API: server { listen 80; server_name your_server_domain; l…...

机器学习算法如何进行特征重要性评估
特征重要性评估是机器学习中一种常用的方法,用于确定输入特征对模型预测的贡献程度。以下是几种常见的机器学习算法进行特征重要性评估的方法: 1 决策树算法(如随机森林和梯度提升树):决策树算法可以通过计算每个特征…...

运行启动vue项目报报错node: --openssl-legacy-provider is not allowed in NODE_OPTIONS解决
报错的问题就是package.json中的Scripts下的dev 解决方法就是要不升级你的应用代码,支持 新版本的node.js 要不就是删除SET NODE_OPTIONS--openssl-legacy-provider &&代码,如下代码即可正常运行起来...

网工学习5 交换机端口相关配置
交换机的接口属性默认支待一般网络环境,一般情况下是不需要对其接口进行设置的。在某些情况下需 要对其端口属性进行配置时,配置的对象主要有接口隔离、速率、双工等信息。 5.1 接口隔离设置 > 配置接口 GE0/0/1 和 GE0/0/2 的接口隔离功能…...

使用Pytorch从零开始实现CLIP
生成式建模知识回顾: [1] 生成式建模概述 [2] Transformer I,Transformer II [3] 变分自编码器 [4] 生成对抗网络,高级生成对抗网络 I,高级生成对抗网络 II [5] 自回归模型 [6] 归一化流模型 [7] 基于能量的模型 [8] 扩散模型 I, 扩散模型 II…...

Java网络编程 *TCP与UDP协议*
网络编程 什么是计算机网络? 把分布在不同地理区域的具有独立功能的计算机,通过通信设备与线路连接起来,由功能完善的软件实现资源共享和信息传递的系统 简单来说就是把不同地区的计算机通过设备连接起来,实现不同地区之前的数据传输 网络编程是干什么的? 网络…...

校园外卖小程序源码系统 附带完整的搭建教程
随着大学生消费水平的提高,对于外卖服务的需求也在不断增加。很多学生都面临着课业繁重、时间紧张等问题,无法亲自到餐厅就餐。因此,开发一款适合校园外卖市场的应用软件,将为广大学生提供极大的便利。 以下是部分代码示例&#…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

Python异步编程:深入理解协程的原理与实践指南
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 持续学习,不断…...

21-Oracle 23 ai-Automatic SQL Plan Management(SPM)
小伙伴们,有没有迁移数据库完毕后或是突然某一天在同一个实例上同样的SQL, 性能不一样了、业务反馈卡顿、业务超时等各种匪夷所思的现状。 于是SPM定位开始,OCM考试中SPM必考。 其他的AWR、ASH、SQLHC、SQLT、SQL profile等换作下一个话题…...
