【FPGA】Verilog:BCD 加法器的实现

0x00 XOR 运算在 2 的补码加减法中的应用
2 的补码加减法的特点是,当从某个数中减去负数时,将其转换为正数的加法来计算,并将减去正数的情况转换为负数的加法来计算,从而将所有减法运算转换为加法运算。在这种情况下,两个数的加法运算中产生进位的情况是在加法位的所有位都为 1 时。
换句话说,可以使用 AND 门来检测产生进位的情况。在两个数的加法运算中,进位传播的情况是在加法位的两个位中只有一个被设置为 1 时。这是因为从较低位传递上来的进位位会再次传递到下一个位,因此可以使用 XOR 门来检测进位传播的情况。
- carry-generate funciton:
- carry-propagate function:
0x01 BCD 运算
在 BCD 中,使用4位值作为操作数,但由于只表示 0 到 9 的数字,因此只使用 0000 到 1001 的二进制数,而不使用 1010 到 1111 的二进制数(don't care)。
因此,不能使用常规的 2'complement 运算来计算,需要额外的处理:如果 4 位二进制数的运算结果在 1010 到 1111 的范围内,需要将 6 (即 0110),添加到运算结果中。
| BCD 运算例子 |
|
|
0x02 BCD 加法器的实现
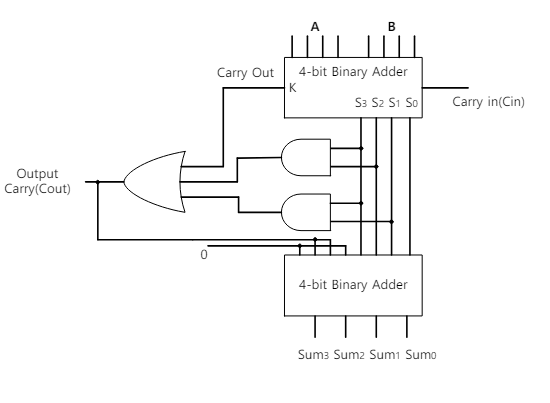
关于 BCD 加法器的结果和模拟过程进行说明(Verilog源代码,输出示例,详细描述过程)。
💬 Design source:
module BCD2(input Cin,input a1,input a2,input a3,input a4,input b1,input b2,input b3,input b4,output sum1,output sum2,output sum3,output sum4,output cout);
wire s1,s2,s3,s4;
wire c1,c2,c3,c4;
wire C1,C2,C3,C4;assign s1 = (a1^b1)^Cin;
assign c1 = (Cin && (a1^b1)) || (a1 && b1);assign s2 = (a2^b2)^c1;
assign c2 = (c1 && (a2^b2)) || (a2 && b2);assign s3 = (a3^b3)^c2;
assign c3 = (c2 && (a3^b3)) || (a3 && b3);assign s4 = (a4^b4)^c3;
assign c4 = (c3 && (a4^b4)) || (a4 && b4);///
assign cout = (c4 || (s3 && s4) || (s2 && s4));assign sum1 = s1;
assign C1 = (0 && (s1^0)) || (s1 && 0);assign sum2 = (s2^cout)^C1;
assign C2 = (C1 && (s2^cout)) || (s2 && cout);assign sum3 = (s3^cout)^C2;
assign C3 = (C2 && (s3^cout)) || (s3 && cout);assign sum4 = (s4^0)^C3;
assign C4 = (C3 && (s4^0)) || (s4 && 0);endmodule💬 Testbench:
`timescale 1ns / 1psmodule BCD2_tb;
reg Cin,a1,a2,a3,a4,b1,b2,b3,b4;
wire sum1,sum2,sum3,sum4,cout;BCD2 u_BCD2 (.Cin(Cin ),.a1(a1 ),.a2(a2 ),.a3(a3 ),.a4(a4 ),.b1(b1 ),.b2(b2 ),.b3(b3 ),.b4(b4 ),.sum1(sum1 ),.sum2(sum2 ),.sum3(sum3 ),.sum4(sum4 ),.cout(cout )
);initial beginCin = 1'b0;a1 = 1'b0;a2 = 1'b0;a3 = 1'b0;a4 = 1'b0;b1 = 1'b0;b2 = 1'b0;b3 = 1'b0;b4 = 1'b0;
endalways@(Cin or a1 or a2 or a3 or a4 or b1 or b2 or b3 or b4) beginCin <=#10 ~Cin;a1 <= #20 ~a1;a2 <= #40 ~a2;a3 <= #80 ~a3;a4 <= #160 ~a4;b1 <= #320 ~b1;b2 <= #640 ~b2;b3 <= #1280 ~b3;b4 <= #2560 ~b4;
endinitial begin#5120$finish;
endendmodule🚩 运行结果如下:

📜 Schematic:
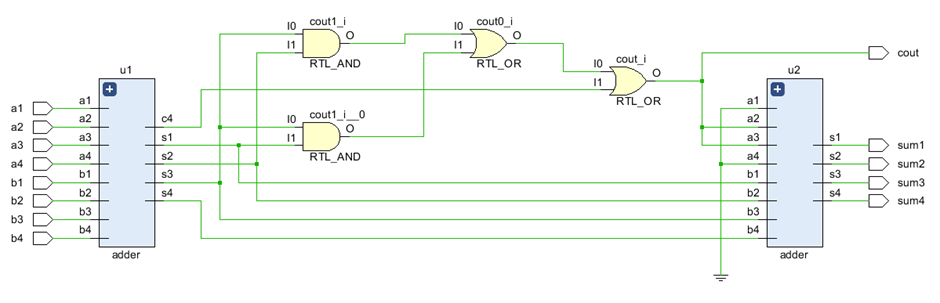 实现的 BCD 加法器是一种将 4 位加法器运算结果转换为 BCD 表示的设备。如果运算结果是一个大于 9 的数字,我们只需加上 6 (0110)。为了实现这一点,该装置由两个加法器电路组成:一个用于执行 4 位加法器运算,另一个电路用于在第一个运算结果大于 9 时加上 0110(补偿电路)。
实现的 BCD 加法器是一种将 4 位加法器运算结果转换为 BCD 表示的设备。如果运算结果是一个大于 9 的数字,我们只需加上 6 (0110)。为了实现这一点,该装置由两个加法器电路组成:一个用于执行 4 位加法器运算,另一个电路用于在第一个运算结果大于 9 时加上 0110(补偿电路)。
0x03 补充:Single-level 16 bit 超前进位加法器
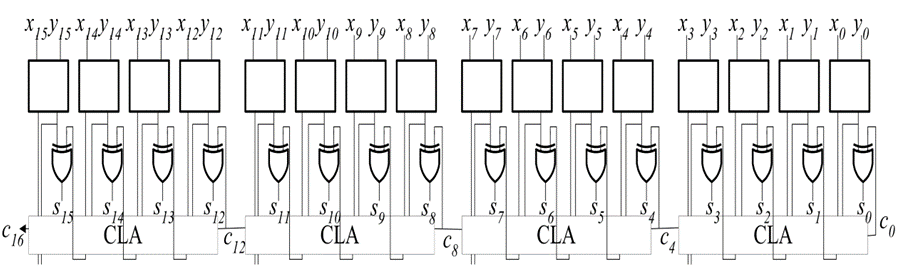
四个 4 位超前进位加法器可以合并成一个 16 位超前进位加法器。它是四个并行结构的串行连接,是并行和串行结构的混合体。
0x04 补充:2-level 16-bit 超前进位加法器

2 级 16 位超前进位加法器是一种通过使用双 CLA 发生器,比单级 16 位超前进位加法器更能减少通过栅极所需的延迟的结构。
| 2-level 16-bit Carry Look-ahead Adder |
|
|

📌 [ 笔者 ] 최역우(韩)
📃 [ 更新 ] 2022.9.20
❌ [ 勘误 ] /* 暂无 */
📜 [ 声明 ] 由于作者水平有限,本文有错误和不准确之处在所难免,本人也很想知道这些错误,恳望读者批评指正!| 📜 参考资料 Introduction to Logic and Computer Design, Alan Marcovitz, McGrawHill, 2008 Microsoft. MSDN(Microsoft Developer Network)[EB/OL]. []. . 百度百科[EB/OL]. []. https://baike.baidu.com/. |
相关文章:

【FPGA】Verilog:BCD 加法器的实现
0x00 XOR 运算在 2 的补码加减法中的应用 2 的补码加减法的特点是,当从某个数中减去负数时,将其转换为正数的加法来计算,并将减去正数的情况转换为负数的加法来计算,从而将所有减法运算转换为加法运算。在这种情况下,…...
机器学习第15天:GBDT模型
☁️主页 Nowl 🔥专栏《机器学习实战》 《机器学习》 📑君子坐而论道,少年起而行之 文章目录 GBDT模型介绍 Boosting 残差 GBDT的缺点 python代码实现 代码 模型参数解释 结语 GBDT模型介绍 GBDT(Gradient Boos…...

STM32F407-14.3.9-01输出比较模式
输出比较模式 此功能用于控制输出波形,或指示已经过某一时间段。 当捕获/比较寄存器与计数器之间相匹配时,输出比较功能: ● 将为相应的输出引脚分配一个可编程值,该值由输出比较模式(TIMx_CCMRx 寄存器中的 OCxM⑦…...
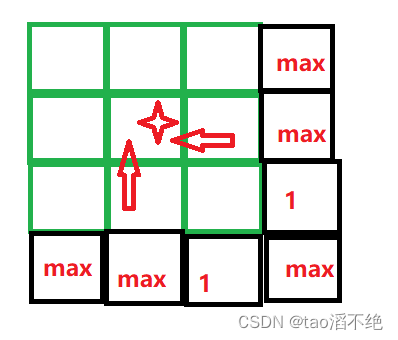
LeetCode题:174. 地下城游戏
目录 一、题目要求 二、解题思路 (1)状态表示 (2)状态转移方程 (3)初始化dp表 (4)填表顺序 (5)返回值 三、代码 一、题目要求 174. 地下城游戏 恶魔们…...
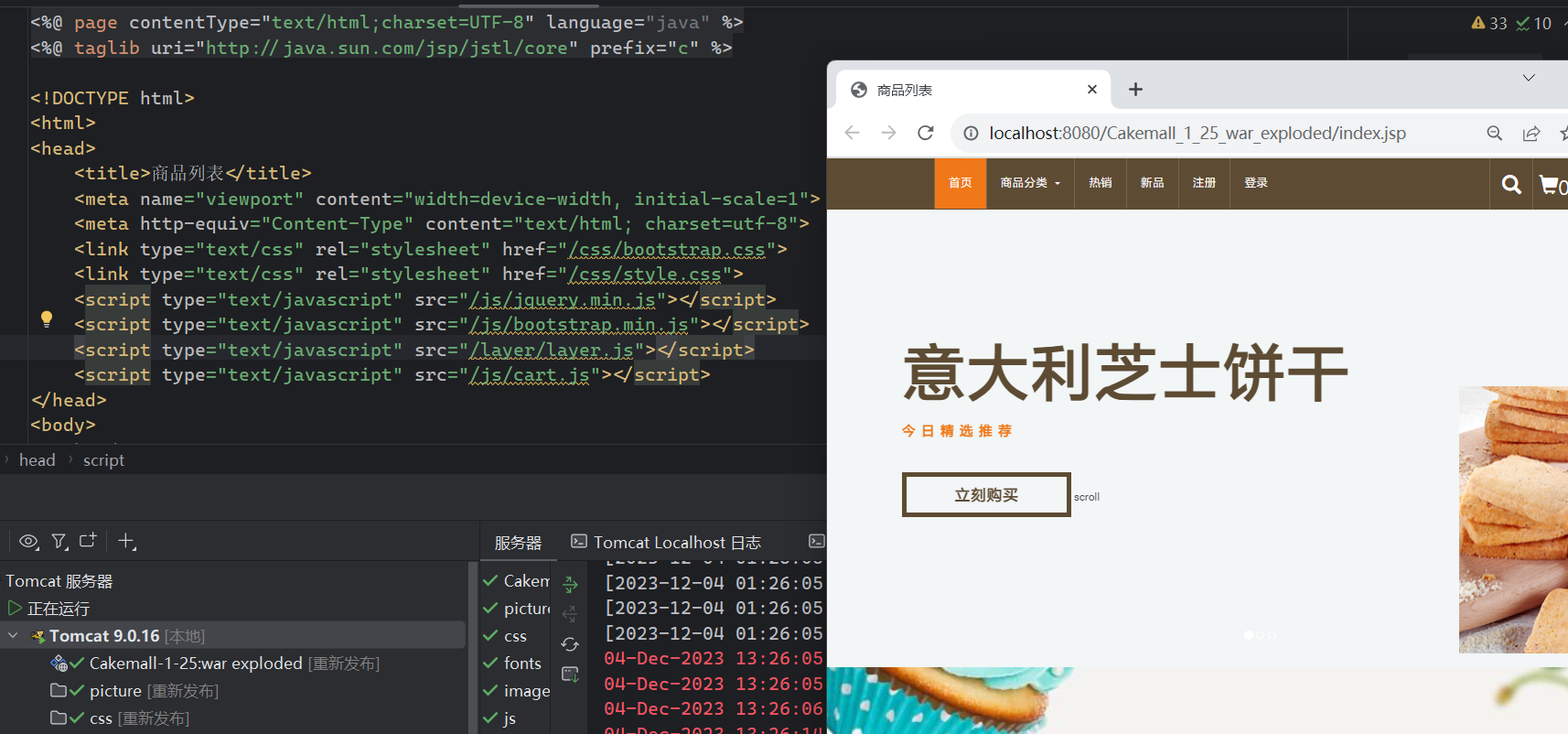
CSS、JS文件无法正确加载至页面问题与解决
目录 1. 问题出现 2. 分析与解决 3. 总结 1. 问题出现 自己在写项目是时候,想启动浏览器查询首页面index.jsp的显示效果 预期效果应该是下面这样的: 但是实际上是这样的: 意思也就是说可能是关于CSS、JS相关的引入方面出了问题ÿ…...
ftp的服务安装配置
安装 yum install -y vsftpd # 是否安装成功 rpm -qa | grep vsftpd # 是否开机启动 systemctl list-unit-files | grep vsftpd # 开机启动 systemctl enable vsftpd.service # ftp端口 netstat -antup | grep ftp # 状态 service vsftpd status service vsftpd start service…...
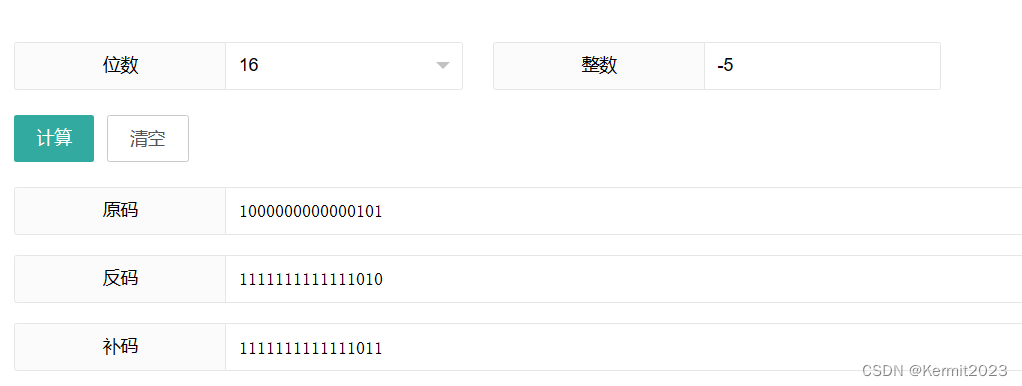
原码,补码,反码(极简版)
原码补码反码 都有符号位,0表示正数,1表示负数 正数 正数的原码,补码,反码都相同 负数 负数的原码,最高位是1,其余的用正常二进制表示 负数的反码,对原码进行符号位不变,其余位…...

uniapp监听wifi连接状态
在uniapp中检测WiFi连接状态可以使用uni的API进行操作。 uni.onNetworkStatusChange((res) > { console.log(res)uni.getConnectedWifi({success: function(res) {console.log(已连接WIFI, res);},fail: function(err) {console.log(未连接WIFI, err);}}); }) 此函数将返回…...
)
2023年总结和2024年展望(以ue为主攻)
2023年就要过去了,总结下: 先说好的地方 1,pbr材质集成到了osg中,加上直接光和间接光。终于知道pbr咋回事了。光线追踪的视频也跟着敲了一个。 2,得到了认可。拿到了半年奖,leader让我明年和架构师一起进行…...

南京大学计算机学院面试准备
该内容是我面试南京大学计算机学院保研的时候的准备题目,最后是面试的时候问到的问题。 目录 1. 自我介绍2. 进程和线程的区别3. 循环引用4. 操作系统怎么利用多核?5. 英文介绍二叉搜索树6. 英文介绍二叉搜索树的时间复杂度7. 介绍 stackover flow8. 什…...
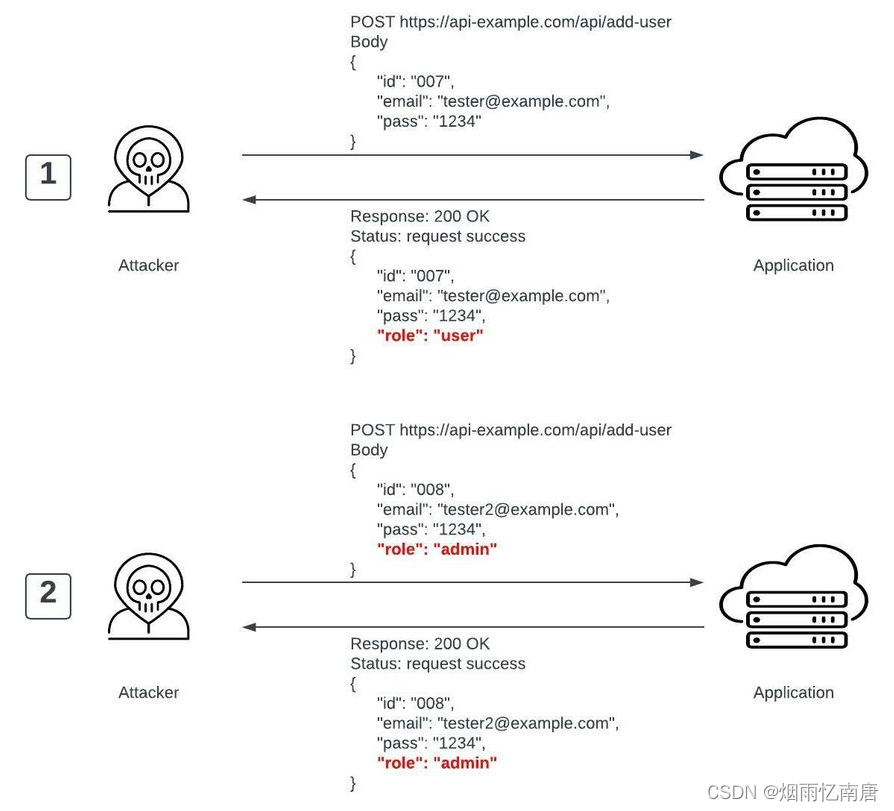
API成批分配漏洞介绍与解决方案
一、API成批分配漏洞介绍 批量分配:在API的业务对象或数据结构中,通常存在多个属性,攻击者通过篡改属性值的方式,达到攻击目的。比如通过设置user.is_admin和user.is_manager的值提升用户权限等级;假设某API的默认接口…...

跨网文件摆渡系统:安全、可控的数字传输桥梁
在企业高度信息化的时代,数据的流通与共享已经成为企业、组织乃至个人之间不可或缺的沟通方式。然而,在数据流通的过程中,我们经常会遇到各种难题和挑战,尤其是当涉及到不同网络环境之间的文件传输。这不仅需要保证文件的安全性&a…...

线程池的原理和基本使用~
线程池的基本原理: 无论是之前在JavaSE基础中,我们学习过的常量池,还是在操作数据库时,我们学习过数据库连接池,以及接下来要学习的线程池,均是一种池化思想,其目的就是为了提高资源的利用率&a…...
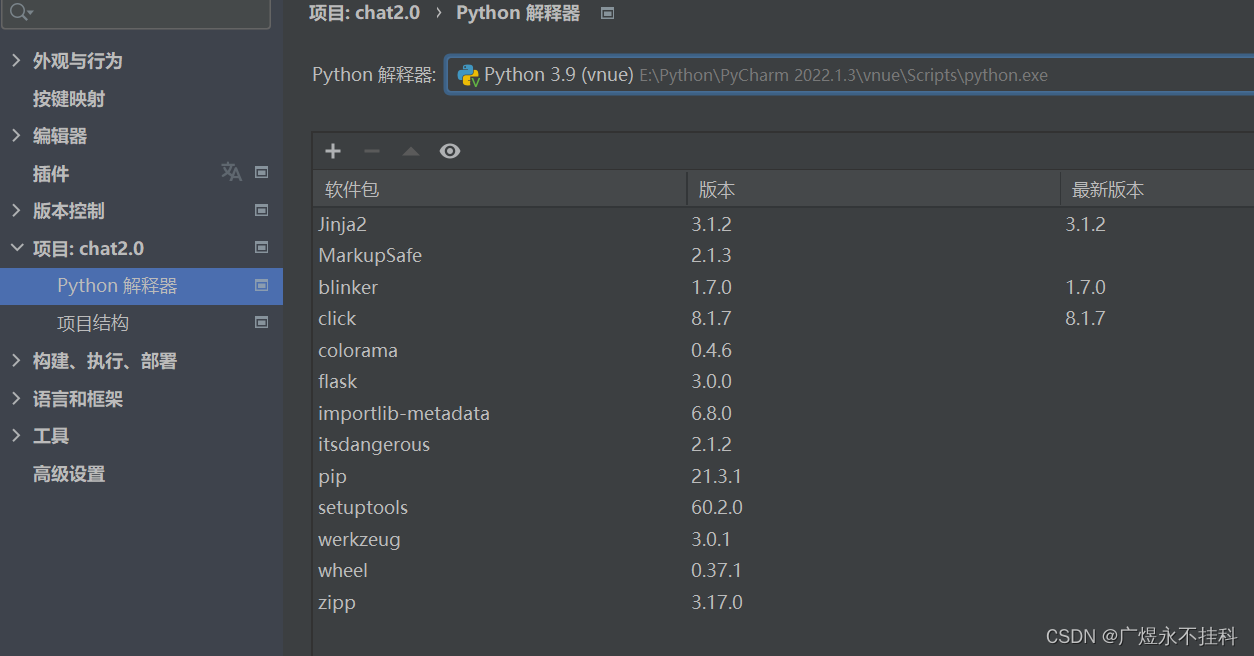
PyTorch2.0环境搭建
一、安装python并配置环境变量 1、打开python官网,下载并安装 Welcome to Python.org 下载 寻找版本:推荐使用3.9版本,或其他表中显示为安全(security)的版本 安装:(略) 2、配置环…...

figma 基础使用 —— 常用方法
一、 导入组件 分成两种方式 (1)离线的包导入(iOS 常用组件.fig 直接拖拽到figma最近网页) (2)在插件市场下载https://www.figma.com/community 二、figma中使用标尺 快捷键:shift R 三、插件…...

linux rsync 和scp区别
rsync 和 scp 都是 Linux 中用于文件复制的命令,但它们之间存在一些关键差异: 效率:rsync 在复制文件时,只会复制文件中改变的部分,而 scp 则会复制整个文件,即使文件只有一小部分发生了变化。因此…...

mac如何永久设置环境变量
1. 先将默认shell修改为bash mac修改默认shell为bash-CSDN博客 2. 修改环境变量 Mac中的环境变量介绍 Mac系统的环境变量,加载顺序为: /etc/profile /etc/paths ~/.bash_profile ~/.bash_login ~/.profile ~/.bashrc 当然/etc/profile和/etc/paths…...
小程序一键生成工具哪个好?
在这个数字化时代,小程序已经成为商家吸引客户、提升业务的重要工具。但是,传统的小程序开发方式既费时又费力,让许多商家望而却步。 现在,有了乔拓云小程序模板开发平台,一切都变了。 乔拓云提供了大量精心设计的模板…...

Ubuntu环境下使用nginx实现强制下载静态资源
安装Nginx sudo apt update sudo apt install nginx关闭防火墙 sudo ufw allow Nginx HTTP修改nginx配置 cd /etc/nginx/conf.d vi nginx.conf在http配置中添加(/your path/为需要下载的文件路径) server {listen 80;server_name localhost;location / {root /your path/…...

苹果 macOS 14.1.2 正式发布 更新了哪些内容?
苹果今日向 Mac 电脑用户推送了 macOS 14.1.2 更新(内部版本号:23B92 | 23B2091),本次更新距离上次发布隔了 28 天。 需要注意的是,因苹果各区域节点服务器配置缓存问题,可能有些地方探测到升级更新的时间略…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...


