LeetCode题:174. 地下城游戏
目录
一、题目要求
二、解题思路
(1)状态表示
(2)状态转移方程
(3)初始化dp表
(4)填表顺序
(5)返回值
三、代码
一、题目要求
174. 地下城游戏
恶魔们抓住了公主并将她关在了地下城
dungeon的 右下角 。地下城是由m x n个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快解救公主,骑士决定每次只 向右 或 向下 移动一步。
返回确保骑士能够拯救到公主所需的最低初始健康点数。
注意:任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
示例 1:
输入:dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]] 输出:7 解释:如果骑士遵循最佳路径:右 -> 右 -> 下 -> 下 ,则骑士的初始健康点数至少为 7 。示例 2:
输入:dungeon = [[0]] 输出:1
二、解题思路
这题我们用到动态规划的思想,分析题目,我们要从左上角走到右下角,求我们最小初始健康点数是多少。
(1)状态表示
按往常经验,我们喜欢以某个点为终点,填这个位置在dp表中的值是多少,因为在这里,如果以某个点为终点,从前面到这个位置所需要的最小健康点数,就是前面消耗健康点数到这个位置还剩1个健康点数,但到这个位置还剩一个健康点数,要是没到右下角呢,还要走好多步,肯定是还没到右下角就已经死掉了。
所以,这里的状态表示:定义以某个位置为起点,到达右下角所需要的最小健康点数。
(2)状态转移方程
如图:

我们想在dp表的四角星位置放值,放的是在原表中从四角星位置到右下角所需最小健康点数,那么,我们知道每个dp表放的都是当前位置到右下角所需健康的最小点数,设当前点数为x,要能从当前位置走到右下角,那么走到下一个位置时的位置,还有的点数要大于等于下一个位置的点数,设原表为d,有一个新建出的dp表,
所以我们推导出:x + d[ i ][ j ] >= dp[ i + 1 ][ j ] 或 x + d[ i ][ j ] >= dp[ i ][ j + 1 ]
所以,x = dp[ i + 1 ][ j ] - d[ i ][ j ] 或 x = dp[ i ][ j + 1 ] - d[ i ][ j ]
那么我们就要就要从右边或者下边,拿一个点数最小的值,走到下一步还需要的健康点数,当然是少的符合题目要求。
合并:x = min(dp[ i + 1 ][ j ],dp[ i ][ j + 1 ]) - d[ i ][ j ]
特殊情况:当前位置如果是一个很大的正整数,也就是一个大血包,那么x就会算出负数,这时候就不符合我们的预期了,因为当前位置的点数是负数,也可以走到右下角,就不符合题目要求了,负数早就死了,所以我们当前x值大于0时,就不做处理,x还是原来的值,当x值小于等于0时,当前位置就放一个1,至少有血还能继续往下走。
推出:当前位置的值:max(1,x)
(3)初始化dp表
根据我们定义的状态表示,我们要知道下面和左边的dp表值,才能推出当前的dp表值,所以最后一行和最后一列可能会数组越界,我们多加最后一行和最后一列,并且两个位置初始化为1,其他位置初始化为正无穷,如图:
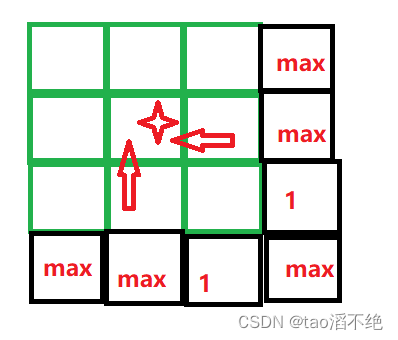
因为,骑士要到右下角,最后至少必须要有1个健康点数,才能到右下角,说明到右下角值至少需要1个健康点数,而其他位置初始化为正无穷是为了不影响最后一行和最后一列填表,比如最后一行,处除了右下角,只能往往右边走,最后一列,只能往下走。所以得到的是右边的dp值,右边的值肯定比正无穷小。
(4)填表顺序
从右到左,从下到上
(5)返回值
return dp[0][0]
三、代码
class Solution {public int calculateMinimumHP(int[][] dungeon) {//1、创建dp表int row = dungeon.length;//行int col = dungeon[0].length;//列int[][] dp = new int[row + 1][col + 1];//2、初始化dp表for(int i = 0; i < col + 1; i++) {//初始化最后一行dp[row][i] = Integer.MAX_VALUE;}dp[row][col - 1] = 1;//最后一行的特殊位置for(int i = 0; i < row + 1; i ++) {//初始化最后一列dp[i][col] = Integer.MAX_VALUE;}dp[row - 1][col] = 1;//最后一列的特殊位置//3、填dp表(顺序:从右到左,从下到上)for(int i = row - 1; i >= 0; i--) {for(int j = col - 1; j >= 0; j--) {int min = Math.min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];dp[i][j] = Math.max(1, min);}}//4、返回值return dp[0][0];}
}相关文章:

LeetCode题:174. 地下城游戏
目录 一、题目要求 二、解题思路 (1)状态表示 (2)状态转移方程 (3)初始化dp表 (4)填表顺序 (5)返回值 三、代码 一、题目要求 174. 地下城游戏 恶魔们…...
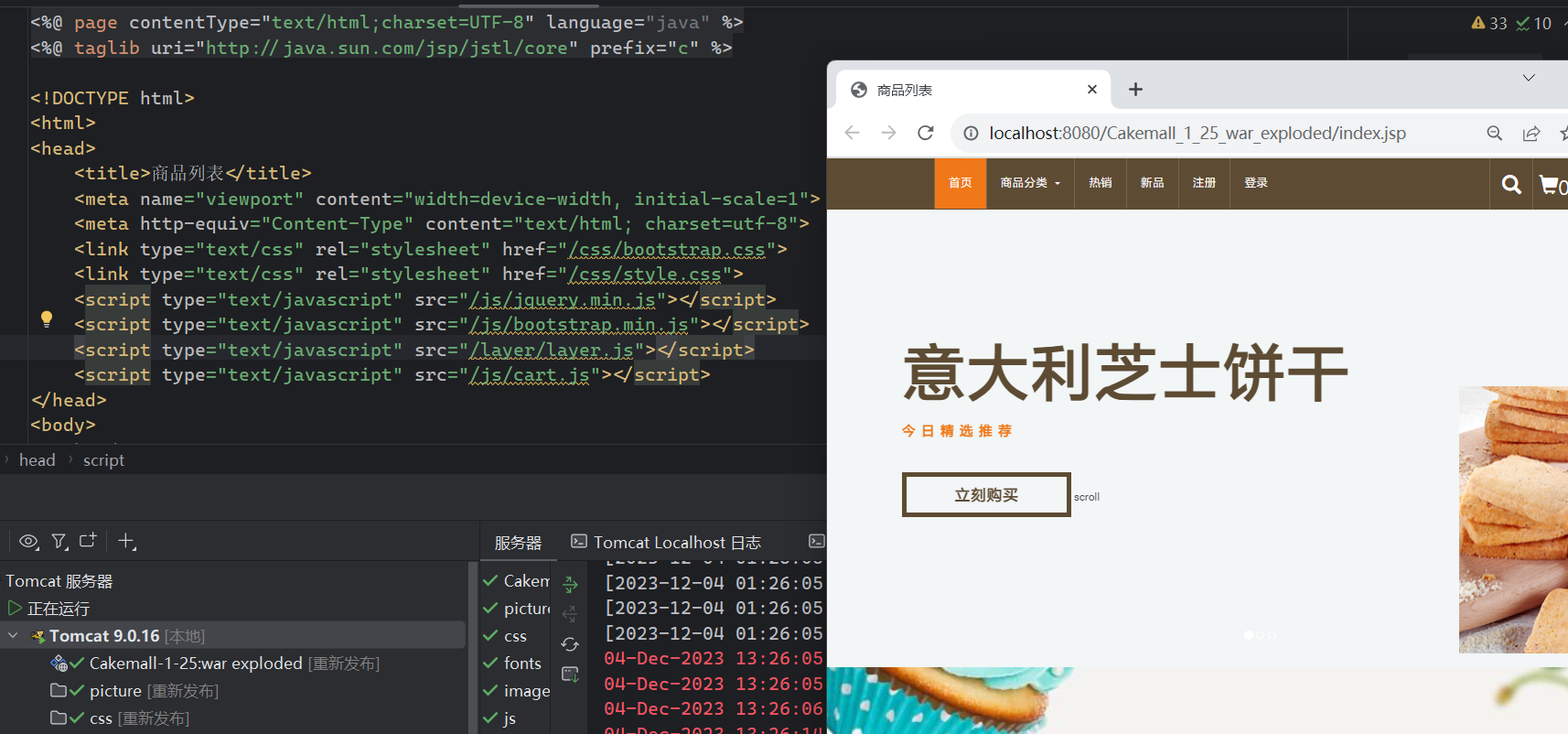
CSS、JS文件无法正确加载至页面问题与解决
目录 1. 问题出现 2. 分析与解决 3. 总结 1. 问题出现 自己在写项目是时候,想启动浏览器查询首页面index.jsp的显示效果 预期效果应该是下面这样的: 但是实际上是这样的: 意思也就是说可能是关于CSS、JS相关的引入方面出了问题ÿ…...
ftp的服务安装配置
安装 yum install -y vsftpd # 是否安装成功 rpm -qa | grep vsftpd # 是否开机启动 systemctl list-unit-files | grep vsftpd # 开机启动 systemctl enable vsftpd.service # ftp端口 netstat -antup | grep ftp # 状态 service vsftpd status service vsftpd start service…...
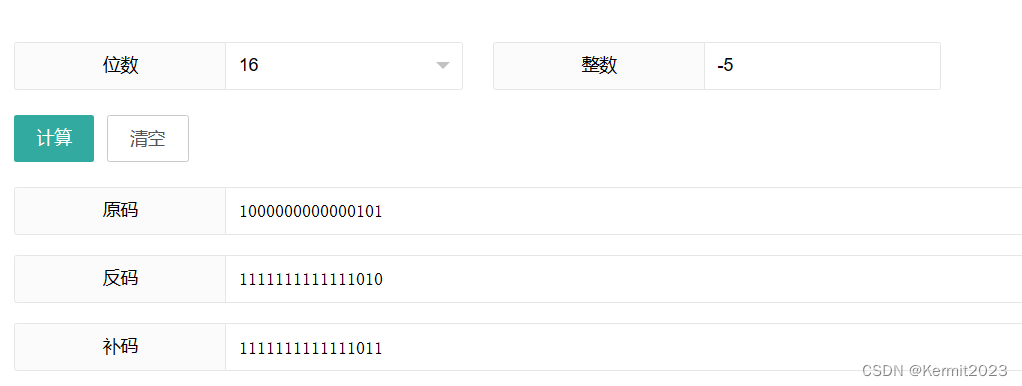
原码,补码,反码(极简版)
原码补码反码 都有符号位,0表示正数,1表示负数 正数 正数的原码,补码,反码都相同 负数 负数的原码,最高位是1,其余的用正常二进制表示 负数的反码,对原码进行符号位不变,其余位…...

uniapp监听wifi连接状态
在uniapp中检测WiFi连接状态可以使用uni的API进行操作。 uni.onNetworkStatusChange((res) > { console.log(res)uni.getConnectedWifi({success: function(res) {console.log(已连接WIFI, res);},fail: function(err) {console.log(未连接WIFI, err);}}); }) 此函数将返回…...
)
2023年总结和2024年展望(以ue为主攻)
2023年就要过去了,总结下: 先说好的地方 1,pbr材质集成到了osg中,加上直接光和间接光。终于知道pbr咋回事了。光线追踪的视频也跟着敲了一个。 2,得到了认可。拿到了半年奖,leader让我明年和架构师一起进行…...

南京大学计算机学院面试准备
该内容是我面试南京大学计算机学院保研的时候的准备题目,最后是面试的时候问到的问题。 目录 1. 自我介绍2. 进程和线程的区别3. 循环引用4. 操作系统怎么利用多核?5. 英文介绍二叉搜索树6. 英文介绍二叉搜索树的时间复杂度7. 介绍 stackover flow8. 什…...
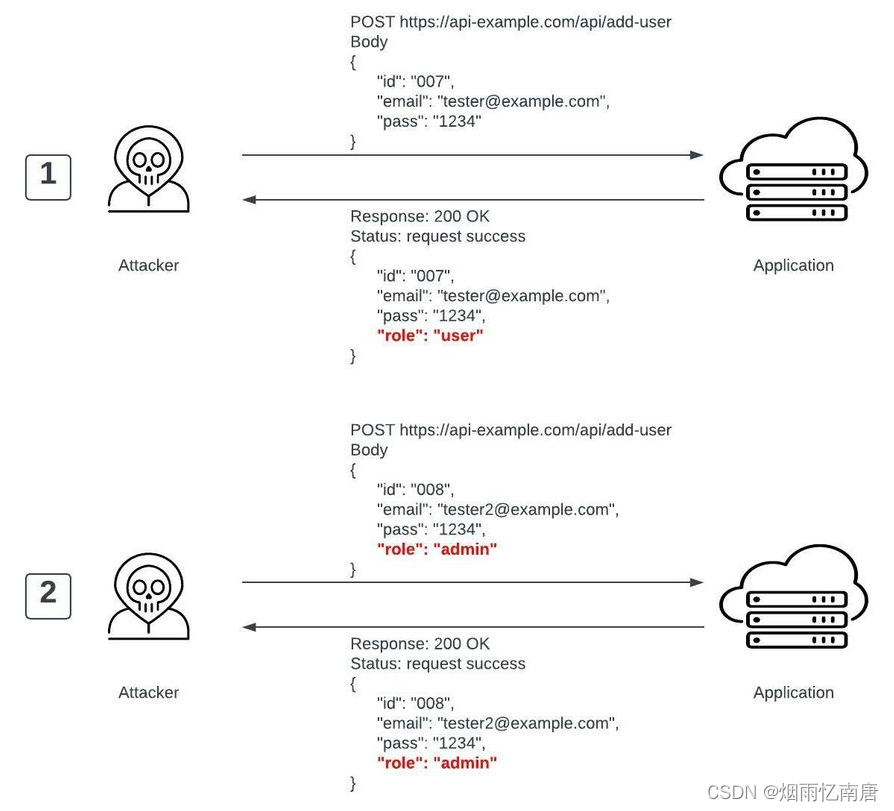
API成批分配漏洞介绍与解决方案
一、API成批分配漏洞介绍 批量分配:在API的业务对象或数据结构中,通常存在多个属性,攻击者通过篡改属性值的方式,达到攻击目的。比如通过设置user.is_admin和user.is_manager的值提升用户权限等级;假设某API的默认接口…...

跨网文件摆渡系统:安全、可控的数字传输桥梁
在企业高度信息化的时代,数据的流通与共享已经成为企业、组织乃至个人之间不可或缺的沟通方式。然而,在数据流通的过程中,我们经常会遇到各种难题和挑战,尤其是当涉及到不同网络环境之间的文件传输。这不仅需要保证文件的安全性&a…...

线程池的原理和基本使用~
线程池的基本原理: 无论是之前在JavaSE基础中,我们学习过的常量池,还是在操作数据库时,我们学习过数据库连接池,以及接下来要学习的线程池,均是一种池化思想,其目的就是为了提高资源的利用率&a…...
PyTorch2.0环境搭建
一、安装python并配置环境变量 1、打开python官网,下载并安装 Welcome to Python.org 下载 寻找版本:推荐使用3.9版本,或其他表中显示为安全(security)的版本 安装:(略) 2、配置环…...

figma 基础使用 —— 常用方法
一、 导入组件 分成两种方式 (1)离线的包导入(iOS 常用组件.fig 直接拖拽到figma最近网页) (2)在插件市场下载https://www.figma.com/community 二、figma中使用标尺 快捷键:shift R 三、插件…...

linux rsync 和scp区别
rsync 和 scp 都是 Linux 中用于文件复制的命令,但它们之间存在一些关键差异: 效率:rsync 在复制文件时,只会复制文件中改变的部分,而 scp 则会复制整个文件,即使文件只有一小部分发生了变化。因此…...

mac如何永久设置环境变量
1. 先将默认shell修改为bash mac修改默认shell为bash-CSDN博客 2. 修改环境变量 Mac中的环境变量介绍 Mac系统的环境变量,加载顺序为: /etc/profile /etc/paths ~/.bash_profile ~/.bash_login ~/.profile ~/.bashrc 当然/etc/profile和/etc/paths…...
小程序一键生成工具哪个好?
在这个数字化时代,小程序已经成为商家吸引客户、提升业务的重要工具。但是,传统的小程序开发方式既费时又费力,让许多商家望而却步。 现在,有了乔拓云小程序模板开发平台,一切都变了。 乔拓云提供了大量精心设计的模板…...

Ubuntu环境下使用nginx实现强制下载静态资源
安装Nginx sudo apt update sudo apt install nginx关闭防火墙 sudo ufw allow Nginx HTTP修改nginx配置 cd /etc/nginx/conf.d vi nginx.conf在http配置中添加(/your path/为需要下载的文件路径) server {listen 80;server_name localhost;location / {root /your path/…...

苹果 macOS 14.1.2 正式发布 更新了哪些内容?
苹果今日向 Mac 电脑用户推送了 macOS 14.1.2 更新(内部版本号:23B92 | 23B2091),本次更新距离上次发布隔了 28 天。 需要注意的是,因苹果各区域节点服务器配置缓存问题,可能有些地方探测到升级更新的时间略…...
【网络编程】-- 02 端口、通信协议
网络编程 3 端口 端口表示计算机上的一个程序的进程 不同的进程有不同的端口号!用来区分不同的软件进程 被规定总共0~65535 TCP,UDP:65535 * 2 在同一协议下,端口号不可以冲突占用 端口分类: 公有端口:0~1023 HT…...

数字发射链路噪声系数核算方法、实例与matlab程序
前言 发射链路各器件噪声性能较差会影响发射信号信噪比,从而导致较高的误码率,通过定量的分析发射链路噪声系数与信噪比恶化的关系,能够在设计过程中进行合理的评估和处理。 一、发射链路噪声 发射链路的噪声从特性上可以大致分为࿱…...
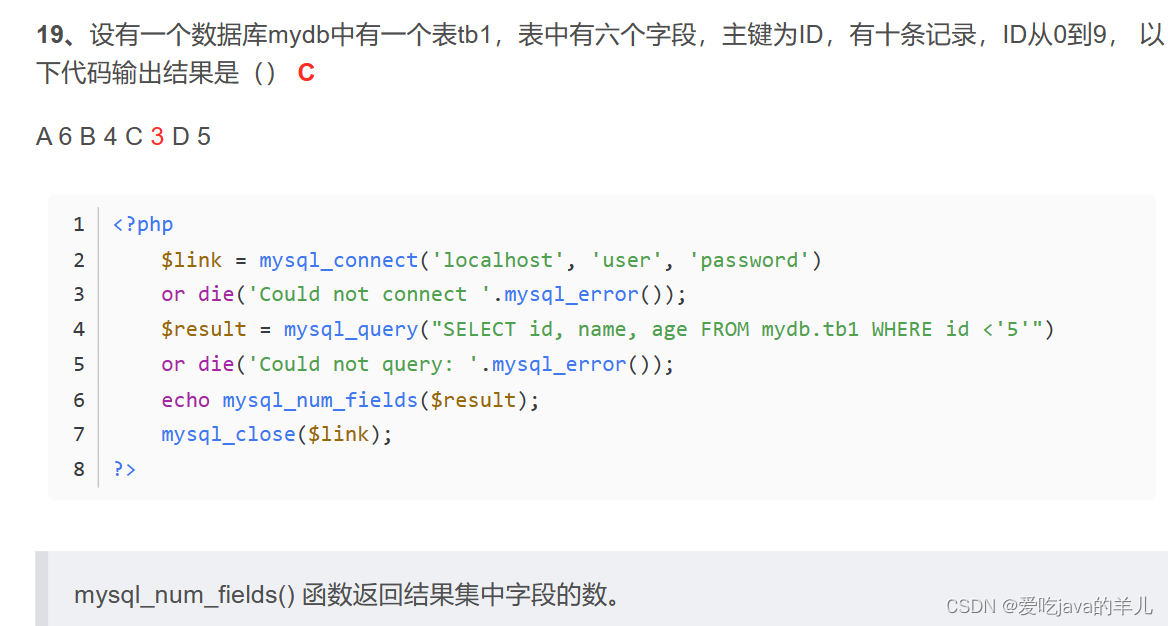
SQL数据库知识点总结归纳
前后顺序可以任意颠倒,不影响库中的数据关系 关系数据库的逻辑性强而物理性弱,因此关系数据库中的各条记录前后顺序可以任意颠倒,不影响库中的数据关系 一名员工可以使用多台计算机(1:m),而一台计算机只能被一名员工使用(1:1),所以员工和计算机两个实体之间是一对多…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

倒装芯片凸点成型工艺
UBM(Under Bump Metallization)与Bump(焊球)形成工艺流程。我们可以将整张流程图分为三大阶段来理解: 🔧 一、UBM(Under Bump Metallization)工艺流程(黄色区域ÿ…...

