当前位置： 首页 > news >正文

决策树 算法原理

news 2025/12/20 4:07:01

决策树 算法原理

决策树的原理

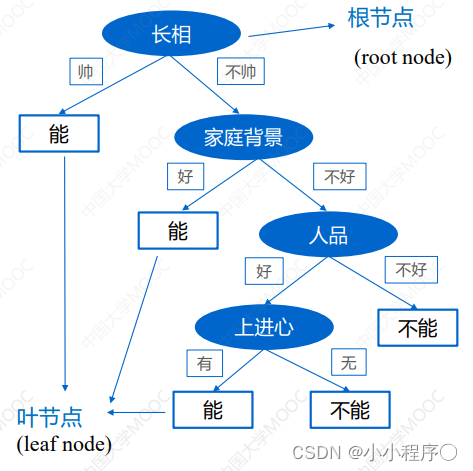
在这里插入图片描述

  • 决策树: 从训练数据中学习得出一个树状结构的模型

  • 决策树属于判别模型

  • 决策树是一种树状结构，通过做出一系列决策 (选择)
    来对数据进行划分，这类似于针对一系列问题进行选择。

  • 决策树的决策过程就是从根节点开始，测试待分类项中对应的特征属性，并按照其值选择输出分支，直到叶子节点，将叶子节点的存放的类别作为决策结果。

  • 决策树算法是一种归纳分类算法它通过对训练集的学习，挖掘出有用的规则，用于对新数据进行预测。

  • 决策树算法属于监督学习方法

  • 决策树归纳的基本算法是贪心算法自顶向下来构建决策树。

  • 贪心算法:在每一步选择中都采取在当前状态下最好/优的选择

  • 在决策树的生成过程中，分割方法即属性选择的度量是关键。

决策树的特点

优点

  • 推理过程容易理解，计算简单，可解释性强
  • 比较适合处理有缺失属性的样本。
  • 可自动忽略目标变量没有贡献的属性变量，也为判断属性变量的重要性减少变量的数目提供参考。
    缺点
  • 容易造成过拟合，需要采用剪枝操作.
  • 忽略了数据之间的相关性。
  • 对于各类别样本数量不一致的数据，信息增益会偏向于那些更多数值的特征

决策树的三种基本类型

  • 建立决策树的关键，即在当前状态下选择哪个属性作为分类依据。根据不同的目标函数，建立决策树主要有一下三种算法: ID3(lterativeDichotomiser)、C4.5CART(Classification And Regression Tree).
    在这里插入图片描述

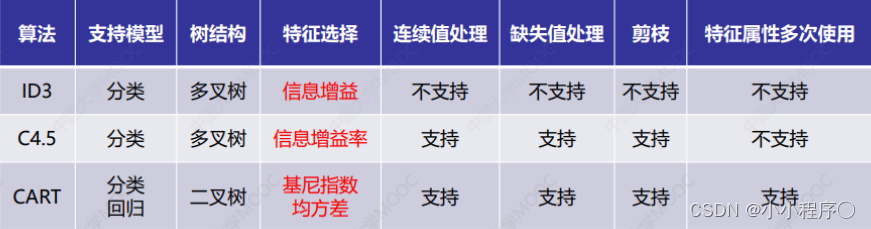
下次博客简述ID3算法、C4.5算法、CART算法

相关文章：

决策树 算法原理

决策树 算法原理 决策树的原理 决策树: 从训练数据中学习得出一个树状结构的模型 决策树属于判别模型 决策树是一种树状结构，通过做出一系列决策 (选择) 来对数据进行划分，这类似于针对一系列问题进行选择。 决策树的决策过程就是从根节点开始&#…...

编程日记 2023/12/9 6:20:46

Git全局设置命令---设置提交人邮箱

介绍 使用git命令设置提交人邮箱。 命令 git config --global user.email "xxxxxxxx.com"...

编程日记 2023/12/9 6:19:46

3DCAT+上汽奥迪：打造新零售汽车配置器实时云渲染解决方案

在 5G、云计算等技术飞速发展的加持下，云渲染技术迎来了突飞猛进的发展。在这样的背景下，3DCAT应运而生，成为了业内知名的实时云渲染服务商之一。 交互式3D实时云看车作为云渲染技术的一种使用场景，也逐步成为一种新的看车方式&a…...

编程日记 2023/12/9 6:18:45

物联网+AI智慧工地云平台源码（SaaS模式）

智慧工地云平台充分运用数字化技术，聚焦施工现场岗位一线，依托物联网、互联网、AI等技术，围绕施工现场管理的人、机、料、法、环五大维度，以及施工过程管理的进度、质量、安全三大体系为基础应用，实现全面高效的工程管…...

编程日记 2023/12/9 6:17:44

python打开相机，用鼠标左键框选矩形区域，支持一次框选多个矩形区域，通过鼠标右标清除上一次画的矩形。

方案一 import cv2# Global variables rectangles [] current_rectangle [] drawing False# Mouse callback function def mouse_callback(event, x, y, flags, param):global rectangles, current_rectangle, drawingif event cv2.EVENT_LBUTTONDOWN:drawing Truecurren…...

编程日记 2023/12/9 6:16:43

卷积之后通道数为什么变了

通道数增多与卷积之后得到的图像特征数量有关 卷积层的作用本来就是把输入中的特征分离出来变成新的 feature map，每一个输出通道就是一个卷积操作提取出来的一种特征。在此过程中ReLU激活起到过滤的作用，把负相关的特征点去掉，把正相关的留…...

编程日记 2023/12/9 6:15:42

ubuntu18.04安装opencv-4.5.5+opencv_contrib-4.5.5

一、安装opencv依赖 sudo apt-get install build-essential sudo apt-get install cmake git libgtk2.0-dev pkg-config libavcodec-dev libavformat-dev libswscale-dev sudo apt-get install python-dev python-numpy libtbb2 libtbb-dev libjpeg-dev libpng-dev libtiff-d…...

编程日记 2023/12/9 6:13:41

实验3.5 路由器的单臂路由配置

实验3.5 路由器的单臂路由配置 一、任务描述二、任务分析三、具体要求四、实验拓扑五、任务实施1.SWA的基本配置2.RA的基本配置3.在RA上查看接口状态 六、任务验收七、任务小结 一、任务描述 某公司对部门划分了需VLAN之后，发现两个部门之间无法通信，但…...

编程日记 2023/12/9 6:12:40

nodejs微信小程序＋python＋PHP的基于大数据的家电销售分析系统设计与实现-计算机毕业设计推荐django

目 录 摘 要 I ABSTRACT II 目 录 II 第1章 绪论 1 1.1背景及意义 1 1.2 国内外研究概况 1 1.3 研究的内容 1 第2章 相关技术 3 2.1 nodejs简介 4 2.2 express框架介绍 6 2.4 MySQL数据库 4 第3章 系统分析 5 3.1 需求分析 5 3.2 系统可行性分析 5 3.2.1技术可行性：…...

编程日记 2023/12/9 6:10:36

Windows server flask

1、Windows server 通过python的flask执行命令 from flask import Flask, request, abort import subprocess from flask_basicauth import BasicAuth app Flask(__name__) # 获取url是进行账号密码认证，设置url的账号密码 app.config[BASIC_AUTH_USERNAME] 账号…...

编程日记 2023/12/9 6:09:36

maven工程的pom.xml文件中增加了依赖，但偶尔没有下载到本地仓库

maven工程pom.xml文件中的个别依赖没有下载到本地maven仓库。以前没有遇到这种情况，今天就遇到了这个问题，把解决过程记录下来。 我在eclipse中编辑maven工程的pom.xml文件，增加对mybatis的依赖，但保存文件后，依赖的j…...

编程日记 2023/12/9 6:08:33

Navicat 技术指引 | 适用于 GaussDB 分布式的用户/权限功能

Navicat Premium（16.3.3 Windows 版或以上）正式支持 GaussDB 分布式数据库。GaussDB 分布式模式更适合对系统可用性和数据处理能力要求较高的场景。Navicat 工具不仅提供可视化数据查看和编辑功能，还提供强大的高阶功能（如模型、结…...

编程日记 2023/12/9 6:06:31

基于支持向量机SVM的新鲜度等级预测，基于自适应粒子群优化长短期神经网络的新鲜度等级预测

目录 背影 支持向量机SVM的详细原理 SVM的定义 SVM理论 粒子群算法原理 SVM应用实例，基于支持向量机SVM的新鲜度等级预测，基于自适应粒子群优化长短期神经网络的新鲜度等级预测 代码 结果分析 展望 完整代码：基于支持向量机SVM的新鲜度等级预测，基于自适应粒子群优化长短期…...

编程日记 2023/12/9 6:05:30

麒麟系统系统添加路由

系统添加路由 一、路由的解释： 路由工作在OSI参考模型第三层——网络层的数据包转发设备（TCP/IP）路由器根据收到数据包中的网络层地址以及路由器内部维护的路由表决定输出端口以及下一跳地址，并且重写链路层数据包头实现转发数据…...

编程日记 2023/12/9 6:04:30

考研真题数据结构

【2021年山西大学真题】将二叉树中所有非终端结点的左右子树交换位置，可以得到原二叉树的 镜像二叉树，如图。假设二叉树的存储形式为（lchild，data，rchild），给出求镜像二叉树的算法: &#xff0…...

编程日记 2023/12/9 6:03:29

python爬取 HTTP_2 网站超时问题的解决方案

问题背景 在进行网络数据爬取时，使用 Python 程序访问支持 HTTP/2 协议的网站时，有时会遇到超时问题。这可能会导致数据获取不完整，影响爬虫程序的正常运行。 问题描述 在实际操作中，当使用 Python 编写的爬虫程序访问支持 HTT…...

编程日记 2023/12/9 6:01:26

学会用bash在linux写脚本 (二)

接着上一章继续 数值的对比 判断语句 循环语句 22.5 比较、对比、判断 在写脚本时，有时需要做一些比较，例如，两个数字谁大谁小，两个字符串是否相同等。 做对比的表达式有[]、[[]]、test，其中[]和 test这两种表达式的…...

编程日记 2023/12/9 6:00:25

QML中Dialog获取close与open状态

1.新建MyDialog.qml import QtQuick 2.15import QtQuick.Dialogs 1.2Dialog {id: rootvisible: falsetitle: qsTr("弹出对话框")width: 250height: 200} 2.main.qml中调用MyDialog import QtQuick 2.15 import QtQuick.Window 2.15 import QtQuick.Controls 2.15…...

编程日记 2023/12/9 5:59:24

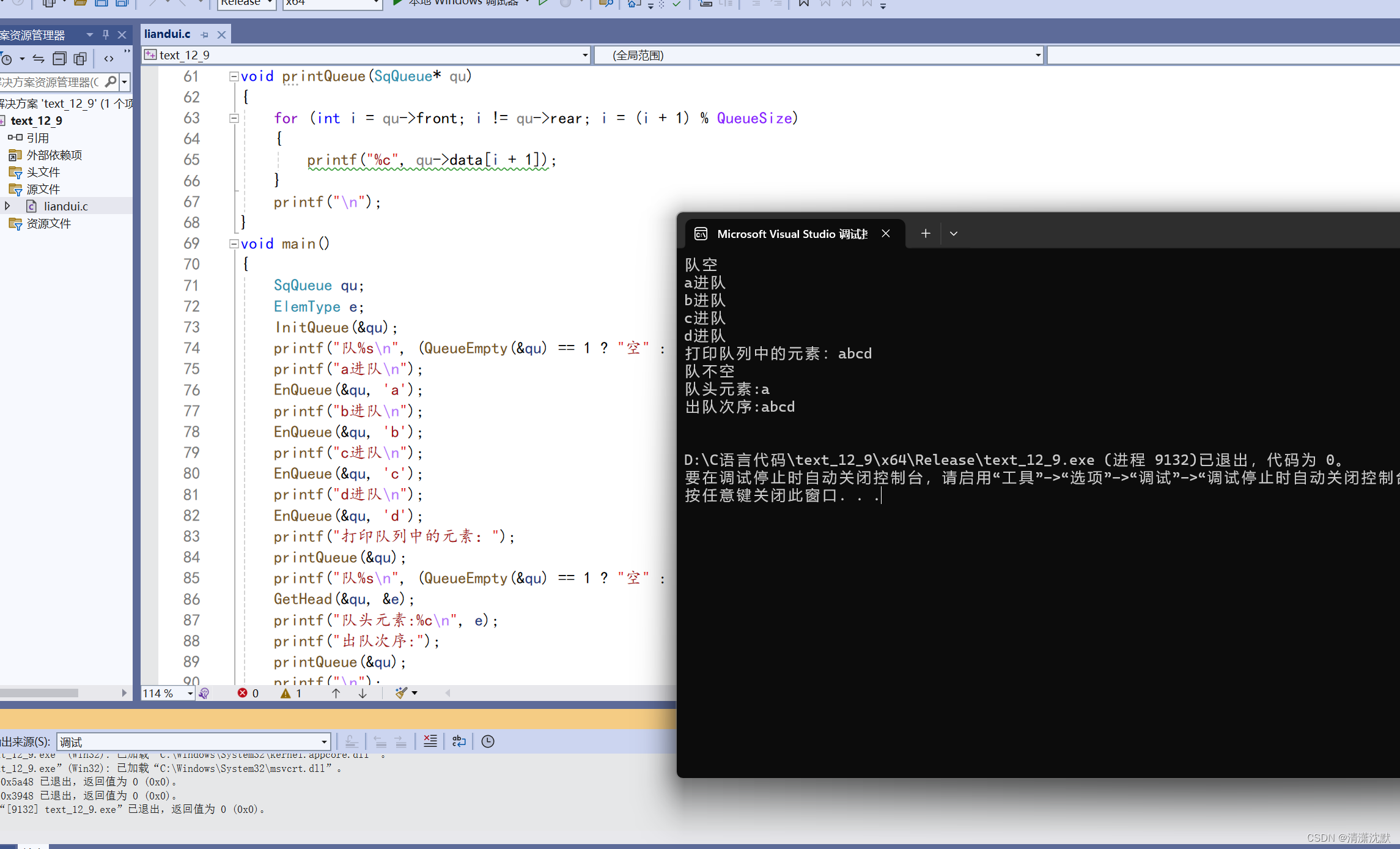
用C语言实现队列的顺序结构

用C语言实现队列的初始化、队列的判空操作、入队操作、出队运算、取队头元素运算、顺序打印队列。 #include<stdio.h> #define QueueSize 100 typedef char ElemType; typedef struct//队列结构体 {ElemType data[QueueSize];//保存队中元素int front, rear;//队头和队尾…...

编程日记 2023/12/9 5:58:23

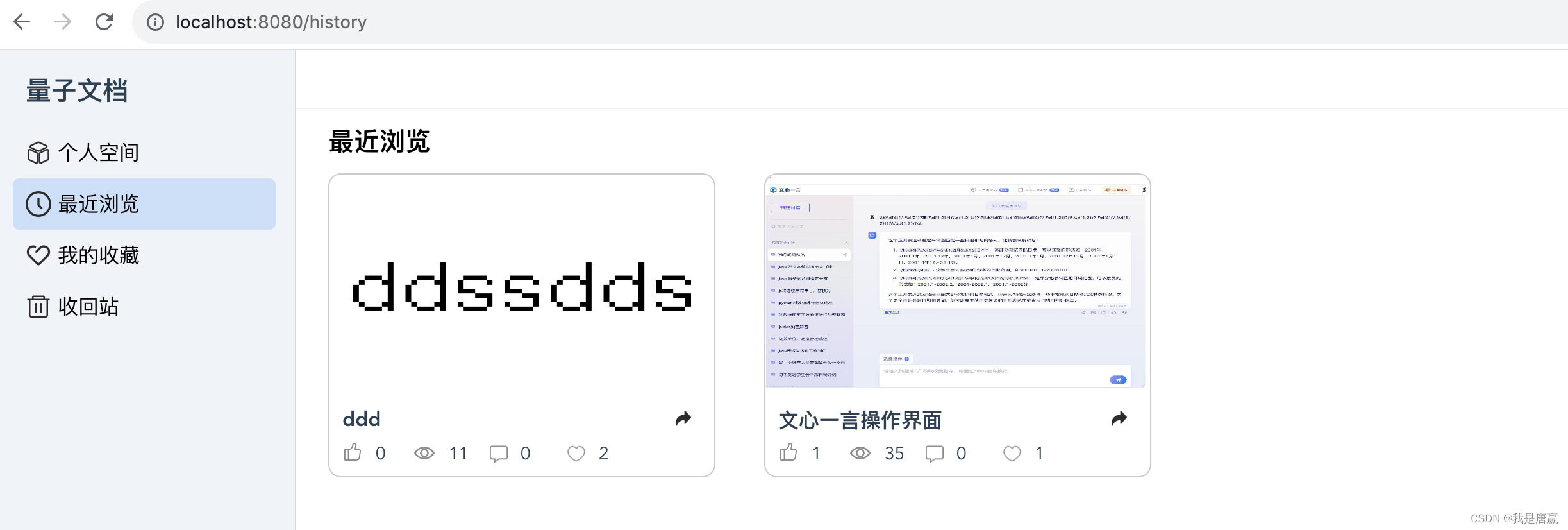
Vue 子路由页面发消息给主路由页面 ，实现主页面显示子页面的信息

需求 子页面进入后&#xff0c;能在主页面显示子页的相关信息&#xff0c;比如说主页面的菜单激活的是哪个子页面的菜单项 如上图&#xff0c;当刷新浏览器页面时&#xff0c;让菜单的激活项仍保持在【最近浏览】。 实现方式&#xff1a; 在子页面的create事件中增加&#xff…...

编程日记 2023/12/9 5:57:22

测试微信模版消息推送

进入“开发接口管理”--“公众平台测试账号”&#xff0c;无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息&#xff1a; 关注测试号&#xff1a;扫二维码关注测试号。 发送模版消息&#xff1a; import requests da…...

编程新知 2025/12/18 11:50:11

深入剖析AI大模型：大模型时代的 Prompt 工程全解析

今天聊的内容&#xff0c;我认为是AI开发里面非常重要的内容。它在AI开发里无处不在&#xff0c;当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗"&#xff0c;或者让翻译模型 "将这段合同翻译成商务日语" 时&#xff0c;输入的这句话就是 Prompt。…...

编程新知 2025/12/19 13:31:20

springboot 百货中心供应链管理系统小程序

一、前言 随着我国经济迅速发展&#xff0c;人们对手机的需求越来越大&#xff0c;各种手机软件也都在被广泛应用&#xff0c;但是对于手机进行数据信息管理&#xff0c;对于手机的各种软件也是备受用户的喜爱&#xff0c;百货中心供应链管理系统被用户普遍使用&#xff0c;为方…...

编程新知 2025/12/10 15:27:46

线程同步：确保多线程程序的安全与高效！

全文目录&#xff1a; 开篇语前序前言第一部分&#xff1a;线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分&#xff1a;synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分&#xff…...

编程新知 2025/9/24 16:02:40

Cinnamon修改面板小工具图标

Cinnamon开始菜单-CSDN博客 设置模块都是做好的&#xff0c;比GNOME简单得多&#xff01; 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

编程新知 2025/12/14 17:38:32

从零实现STL哈希容器：unordered_map/unordered_set封装详解

本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说&#xff0c;直接开始吧&#xff01; 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

编程新知 2025/12/18 4:40:10

实现弹窗随键盘上移居中

实现弹窗随键盘上移的核心思路 在Android中&#xff0c;可以通过监听键盘的显示和隐藏事件&#xff0c;动态调整弹窗的位置。关键点在于获取键盘高度&#xff0c;并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

编程新知 2025/10/6 18:46:56

css3笔记 （1） 自用

outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size&#xff1a;0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格&#xff…...

编程新知 2025/10/11 5:18:43

C/C++ 中附加包含目录、附加库目录与附加依赖项详解

在 C/C 编程的编译和链接过程中&#xff0c;附加包含目录、附加库目录和附加依赖项是三个至关重要的设置&#xff0c;它们相互配合&#xff0c;确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中&#xff0c;这些概念容易让人混淆&#xff0c;但深入理解它们的作用和联…...

编程新知 2025/12/19 23:17:48

C#学习第29天：表达式树（Expression Trees）

目录 什么是表达式树&#xff1f; 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持&#xff1a; 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

编程新知 2025/10/20 9:03:01