线性代数入门与学习笔记
该内容为重拾部分线性代数知识的学习笔记,内容上更多的是为了解决问题而学习的内容,并非系统化的学习。
针对的问题为:Music算法推导求解过程中的矩阵计算知识。
学习的内容包括:矩阵原理、矩阵行列式、矩阵的秩、线性变换矩阵变换、单位矩阵与逆矩阵、特征值和特征向量。
推荐学习视频:bilibili的视频:【线性代数全集从入门到精通(清楚易懂,看过的都说好,哈哈)】 https://www.bilibili.com/video/BV1wL411H7x1/?share_source=copy_web&vd_source=a0df23ab5f45bf4a580c20684f4a6705
一. 矩阵
-
线性方程组
线性方程组,多元x1 x2 x3等组成的线性方程组。线性方程组的解只有三种情况:0个解、1个(组)解和无穷多个解。
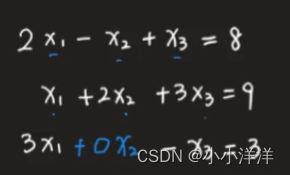
-
增广矩阵
增广矩阵为系数矩阵+常数项矩阵,是一种更简单的表达。

-
理想矩阵:阶梯型矩阵、对角矩阵
通过对矩阵进行初等行变换,即行的倍数、行的叠加、行的倍数再叠加,矩阵的解不变。
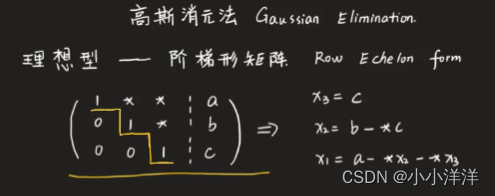
从最下面一行开始消元,得到理想型矩阵可以方便求解元,该方法叫做高斯消元法。
阶梯型矩阵就可以方便求解,对角矩阵则是更加理想的矩阵。
-
矩阵与向量
空间中的向量,可以用多个正交单位向量的组合表示。
多个向量的线性组合为这些向量的向量空间。
线性相关:多个向量的线性组合能够等于0,其中他们的系数不全为0,即线性相关,否则线性无关。
定义:n+1个n维向量一定是线性相关的。因为n个不相关的向量已经组成了整个n维的自由空间,多一个肯定是在这个自由空间中的。
向量的计算:数乘、加法、线性组合。

-
齐次方程组
齐次方程组的常数矩阵为0,即Ax = 0

-
矩阵乘法
矩阵乘法中,左边矩阵的列数要等于右边矩阵的行数。
二、矩阵行列式
- 行列式可以Det(A)表示
- 行列式为符号系数+子矩阵行列式的叠加。
三、矩阵秩
- 秩的定义
矩阵的秩为最高阶非零子式的阶数。

- 秩对求解个数的意义
系数矩阵的秩=增广矩阵的秩:1个解
系数矩阵的秩<增广矩阵的秩:0个解
系数矩阵的秩>增广矩阵的秩:无穷个解
四、线性变换、矩阵变换
- 线性变换和矩阵变换
这两种变换是可以在一定程度上转换的。
五、单位矩阵与逆矩阵
- 单位矩阵

- 逆矩阵
逆矩阵与原矩阵的乘积为单位矩阵。
逆矩阵的计算可以由下述公式计算,分母为矩阵行列式,也可以用Det(A)表示,选取最佳的一行(0比较多的行)进行计算。分子为伴随矩阵。


六、特征值与特征向量
-
特征值和特征向量
矩阵和特征向量的乘积,正好为一个特征值与该特征向量的乘积。即矩阵的乘积,只改变该方向的大小,而不改变方向。
特征向量表达了方向,特征值表达了大小。
个人理解:特征向量意味着该矩阵在这个方向上的映射。

-
特征值计算
Ax = λx
Ax = λIx
(A-λI)x = 0
Det(A-λI) = 0
得到多个特征值 -
特征向量的计算
带入特征值到上式,进行计算和求解。

-
意义
几何意义为变换效果只发生缩放,不发生其他如旋转、平移。
代数意义为矩阵的内部结构进行了分解和化解。
七、协方差矩阵
- 协方差矩阵
个人理解:表达了两个矩阵之间的关联性。
相关文章:

线性代数入门与学习笔记
该内容为重拾部分线性代数知识的学习笔记,内容上更多的是为了解决问题而学习的内容,并非系统化的学习。 针对的问题为:Music算法推导求解过程中的矩阵计算知识。 学习的内容包括:矩阵原理、矩阵行列式、矩阵的秩、线性变换矩阵变换…...

Linux安全学习路标
1. 操作系统基础知识 首先,你需要建立坚实的操作系统基础知识,包括Linux文件系统和目录结构、Linux进程管理、权限管理等基本概念。 2. 网络和通信安全 学习关于网络和通信安全的基础知识,包括TCP/IP协议栈、网络攻击类型、防火墙配置、网…...
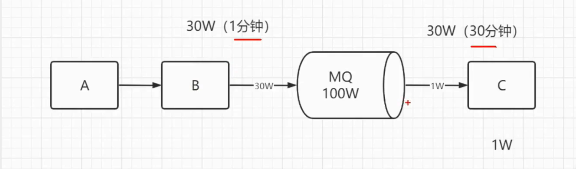
常见的中间件--消息队列中间件测试点
最近刷题,看到了有问中间件的题目,于是整理了一些中间件的知识,大多是在小破站上的笔记,仅供大家参考~ 主要分为七个部分来分享: 一、常见的中间件 二、什么是队列? 三、常见消息队列MQ的比较 四、队列…...

【USRP】5G / 6G OAI 系统 5g / 6G OAI system
面向5G/6G科研应用 USRP专门用于5G/6G产品的原型开发与验证。该系统可以在实验室搭建一个真实的5G 网络,基于开源的代码,专为科研用户设计。 软件无线电架构,构建真实5G移动通信系统 X410 采用了目前流行的异构式系统,融合了FP…...
)
ubuntu20.04设置开机自启动jar(依赖其他服务)
目的: 有的时候我们的项目是部署在物理机上给其他公司员工使用,对于他们来说操作越简单越好。所以我需要实现将我的jar部署在ubuntu上,实现开机自启。(我的项目依赖emqx服务)。 步骤: 切换到system目录 …...

【GEE笔记】在线分类流程,标注样本点、分类和精度评价
GEE在线分类流程 介绍 GEE(Google Earth Engine)是一个强大的地理信息处理平台,可以实现在线的遥感影像分析和处理。本文将介绍如何使用GEE进行在线的分类流程,包括标注样本点、分类和精度评价。本文以2020年5月至8月的哨兵2影像…...
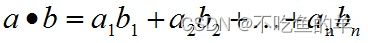
MATLAB基础运算
矩阵和数字相乘 就是矩阵里面每个元素跟这个数字乘一遍 矩阵和矩阵相乘 能不能相乘,需要前面矩阵的列数等于后面矩阵的行数,出来的矩阵大小是前面矩阵的行数*后面矩阵的列数。 所以大家会发现,矩阵相乘如果前后调转了,结果会完全…...

Linux DAC权限的简单应用
Linux的DAC(Discretionary Access Control)权限模型是一种常见的访问控制机制,它用于管理文件和目录的访问权限。作为一名经验丰富的Linux系统安全工程师,我会尽可能以简单明了的方式向计算机小白介绍Linux DAC权限模型。 在Linu…...
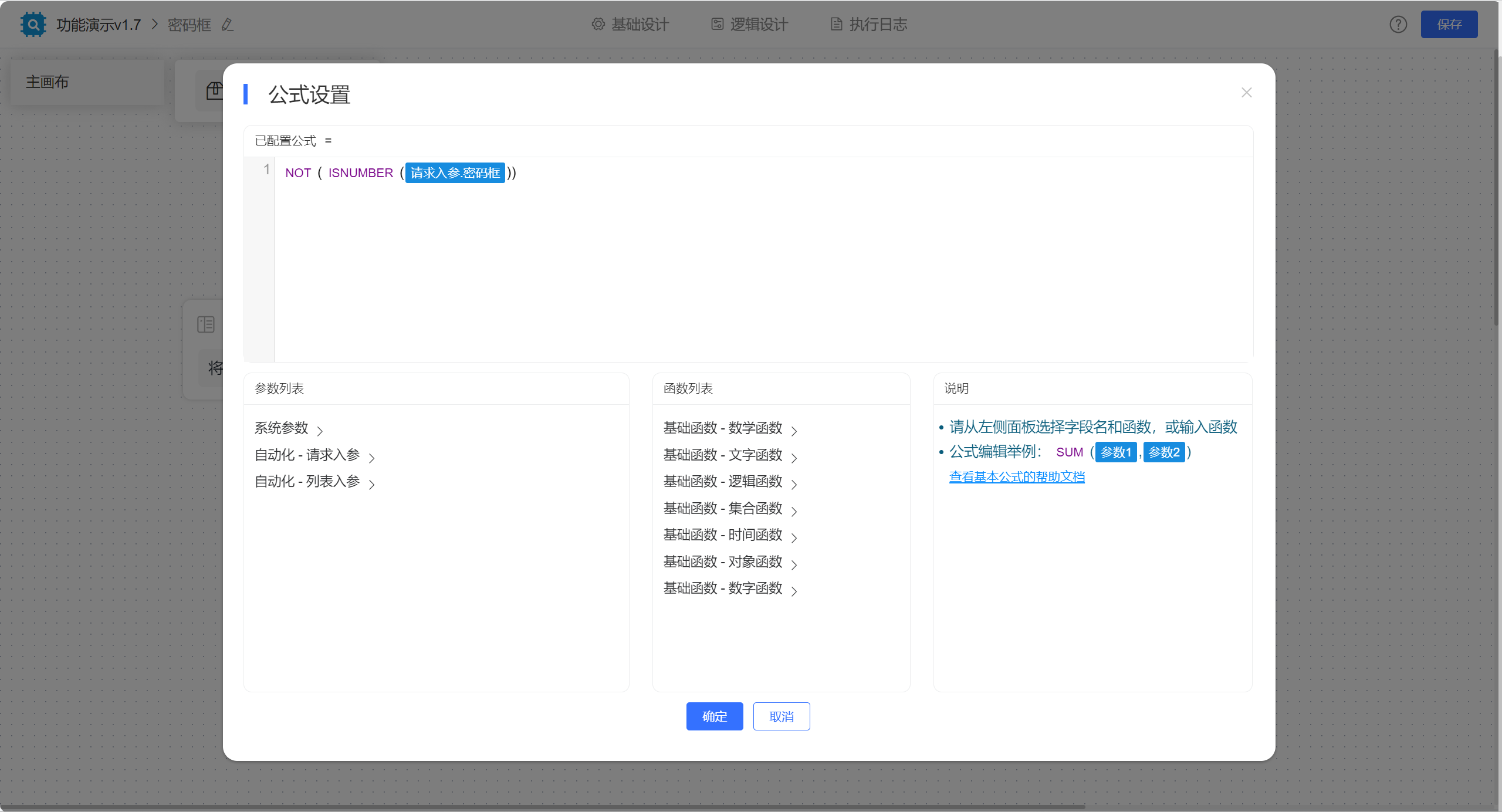
JVS低代码表单引擎:数据校验与处理的先锋
随着信息技术的迅速发展,数据校验与处理已经成为了各类应用中不可或缺的一环。尤其是在涉及敏感信息,如密码处理时,其安全性和准确性显得尤为重要。JVS低代码表单引擎提供了强大的文本组件触发逻辑校验功能,它能够在用户填写数据的…...

clickhouse删除partition分区数据
clickhouse分布式表tencent_table_20231208_DIST,本地表tencent_table_20231208_local; 30台clickhouse存储服务器; 本地表:tencent_table_20231208_local CREATE TABLE tencent_sz.tencent_table_20231208_local (id Int64 DEFA…...

持续集成交付CICD:CentOS 7 安装 Nexus 3.63
目录 一、实验 1.CentOS 7 安装Nexus3.63 二、问题 1.安装Nexus报错 2.Nexus启动停止相关命令 一、实验 1.CentOS 7 安装Nexus3.63 (1)当前操作系统版本&JDK版本 cat /etc/redhat-releasejava -version(2)下载Nexus新…...

Apache Flink(十):Flink集群基础环境搭建-JDK及MySQL搭建
🏡 个人主页:IT贫道_大数据OLAP体系技术栈,Apache Doris,Clickhouse 技术-CSDN博客 🚩 私聊博主:加入大数据技术讨论群聊,获取更多大数据资料。 🔔 博主个人B栈地址:豹哥教你大数据的个人空间-豹哥教你大数据个人主页-哔哩哔哩视频 目录...
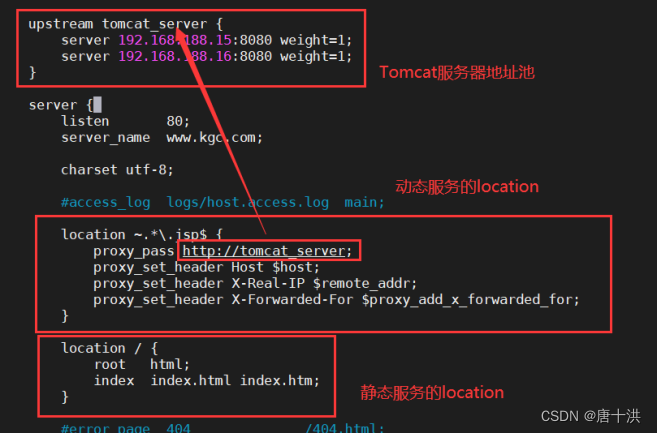
LVS-DR+Keepalived+动静分离实验
架构图 解释一下架构,大概就是用Keepalived实现两台DR服务器的LVS负载均衡,然后后端服务器是两台Nginx服务器两台Tomcat服务器并且实现动静分离这个实验其实就是把 LVS-DRKeepalived 和 动静分离 给拼起来,真的是拼起来,两个部分…...

java面试题-Hashmap、Hashtable、ConcurrentHashMap原理
远离八股文,面试大白话,通俗且易懂 看完后试着用自己的话复述出来。有问题请指出,有需要帮助理解的或者遇到的真实面试题不知道怎么总结的也请评论中写出来,大家一起解决。 java面试题汇总-目录-持续更新中 Hashmap和hashtable存储…...
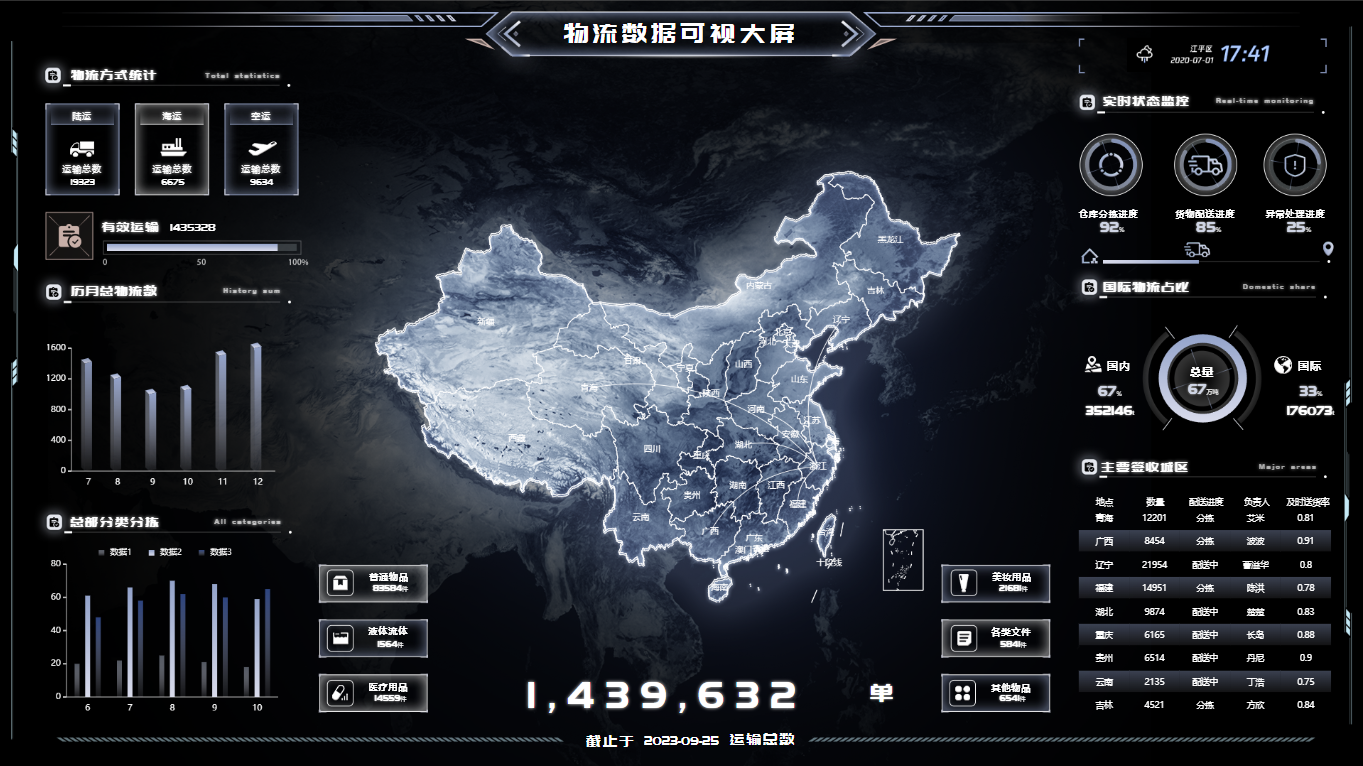
数据可视化:解锁企业经营的智慧之道
在现代企业管理中,数据可视化已经成为了一项重要的工具。它不仅仅是简单地展示数据,更是提供了深入理解数据、做出更明智决策的方法。作为一名可视化设计从业人员,我经手过一些企业自用的数据可视化项目,今天就来和大家聊聊数据可…...

JVM 性能调优
概述篇 面试题 讲讲你理解的性能评价及测试指标?(瓜子) 生产环境中的问题 生产环境发生了内存溢出该如何处理?生产环境应该给服务器分配多少内存合适?如何对垃圾回收器的性能进行调优?生产环境CPU负载飙高…...
)
linux常用命令-yum命令详解(超详细)
文章目录 前言一、yum命令介绍1. yum命令简介2. yum命令的基本语法3. 常用的yum命令选项4. 常用的yum命令参数 二、yum命令示例用法1. 安装软件包2. 更新软件包3. 删除软件包4. 搜索软件包5. 列出已安装的软件包6. 列出可用的软件包7. 清理缓存8. 禁用软件包仓库 总结 前言 yu…...

解决 Element-ui中 表格(Table)使用 v-if 条件切换后,表格的列的筛选不显示了
解决方法 在每个需要使用 v-if 或 v-else 的 el-table-column 上增加 key 作为唯一标识,这样渲染的时候就不会因为复用原则导致列数据混乱了。关于key值,一般习惯使用字段名,也可随机生成一个值,只要具有唯一性就可以。...
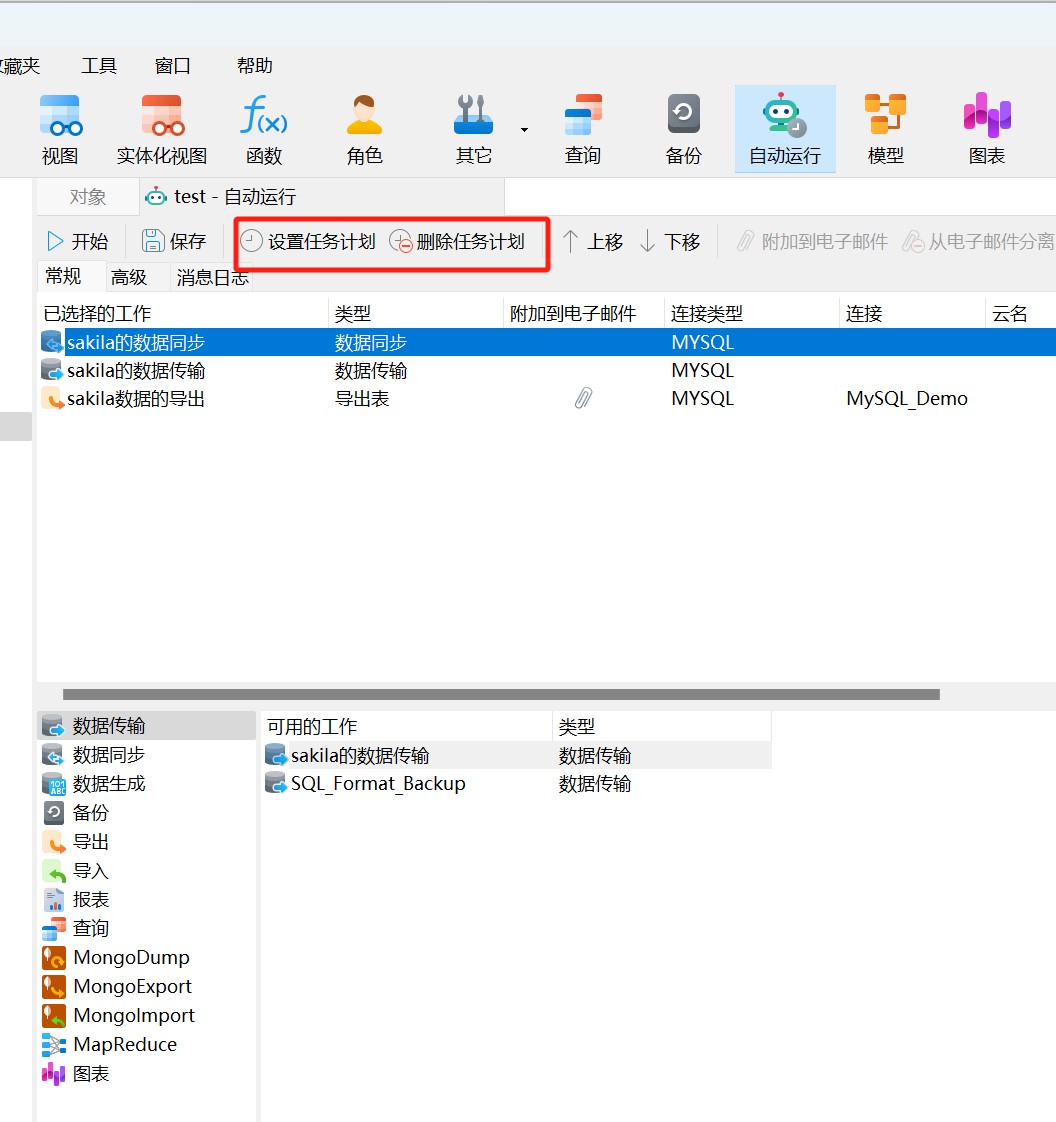
Navicat 技术指引 | 适用于 GaussDB 分布式的自动运行功能
Navicat Premium(16.3.3 Windows 版或以上)正式支持 GaussDB 分布式数据库。GaussDB 分布式模式更适合对系统可用性和数据处理能力要求较高的场景。Navicat 工具不仅提供可视化数据查看和编辑功能,还提供强大的高阶功能(如模型、结…...
爬虫 selenium语法 (八)
目录 一、为什么使用selenium 二、selenium语法——元素定位 1.根据 id 找到对象 2.根据标签属性的属性值找到对象 3.根据Xpath语句获取对象 4.根据标签名获取对象 5.使用bs语法获取对象 6.通过链接文本获取对象 三、selenium语法——访问元素信息 1.获取属性的属性值…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
