最长子序列问题(LCS)--动态规划解法
题目描述:
如果Z既是X的子序列,又是Y的子序列,则称Z为X和Y的公共子序列。
如果给定X、Y,求出Y及其长度。
示例:
输入
ABCPDSFJGODIHJOFDIUSHGD
OSDIHGKODGHBLKSJBHKAGHI输出
SDIHODSHG
9分析:
c[i][j]表示X从0到i与Y从0到j之间公共子序列的长度。
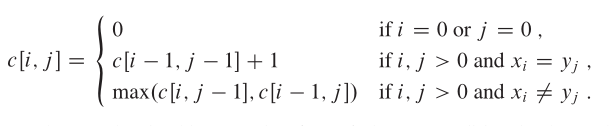
代码 :
//最长子序列问题,不是最长字串问题
#include<iostream>
#include<stack>
using namespace std;const int N = 1000;
int dp[N][N] = { 0 };
int path[N][N];
int main()
{string a, b;cin >> a;cin >> b;int lena = a.size();int lenb = b.size();for (int i = 0; i <lena-1; i++){for (int j = 0; j <lenb-1; j++){if (a[i] == b[j]){dp[i+1][j+1] = dp[i][j] + 1;path[i + 1][j + 1] = 1;}else if (dp[i][j + 1] >= dp[i + 1][j]){dp[i + 1][j + 1] = dp[i][j + 1];path[i + 1][j + 1] = 2;}else{dp[i + 1][j + 1] = dp[i+1][j];path[i + 1][j + 1] = 3;}}}cout << "dp数组为:" << endl;for (int i = 0; i < lena; i++){for (int j = 0; j < lenb; j++){cout << dp[i][j] << ' ';}cout << endl;}cout << "最长子序列数为:" << dp[lena - 1][lenb - 1] << endl;//存放最长子序列stack<char>same;for (int i = lena - 1, j = lenb - 1; i >= 0 && j >= 0;){if (path[i][j] == 1){i--;j--;same.push(a[i]);}else if (path[i][j] == 2){i--;}else{j--;}}cout << "最长子序列为";while (!same.empty()){cout << same.top();same.pop();}cout << endl;system("pause");return 0;}相关文章:
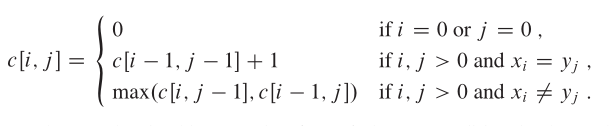
最长子序列问题(LCS)--动态规划解法
题目描述: 如果Z既是X的子序列,又是Y的子序列,则称Z为X和Y的公共子序列。 如果给定X、Y,求出Y及其长度。 示例: 输入 ABCPDSFJGODIHJOFDIUSHGD OSDIHGKODGHBLKSJBHKAGHI 输出 SDIHODSHG 9 分析: c…...

实时流式计算 kafkaStream
文章目录 实时流式计算Kafka StreamKafka Streams 的关键概念KStreamKafka Stream入门案例编写SpringBoot 集成 Kafka Stream 实时流式计算 一般流式计算会与批量计算相比较 流式计算就相当于上图的右侧扶梯,是可以源源不断的产生数据,源源不断的接收数…...

西南科技大学模拟电子技术实验七(集成运算放大器的非线性应用)预习报告
一、计算/设计过程 说明:本实验是验证性实验,计算预测验证结果。是设计性实验一定要从系统指标计算出元件参数过程,越详细越好。用公式输入法完成相关公式内容,不得贴手写图片。(注意:从抽象公式直接得出结果,不得分,页数可根据内容调整) 预习计算内容根据运放的非线…...
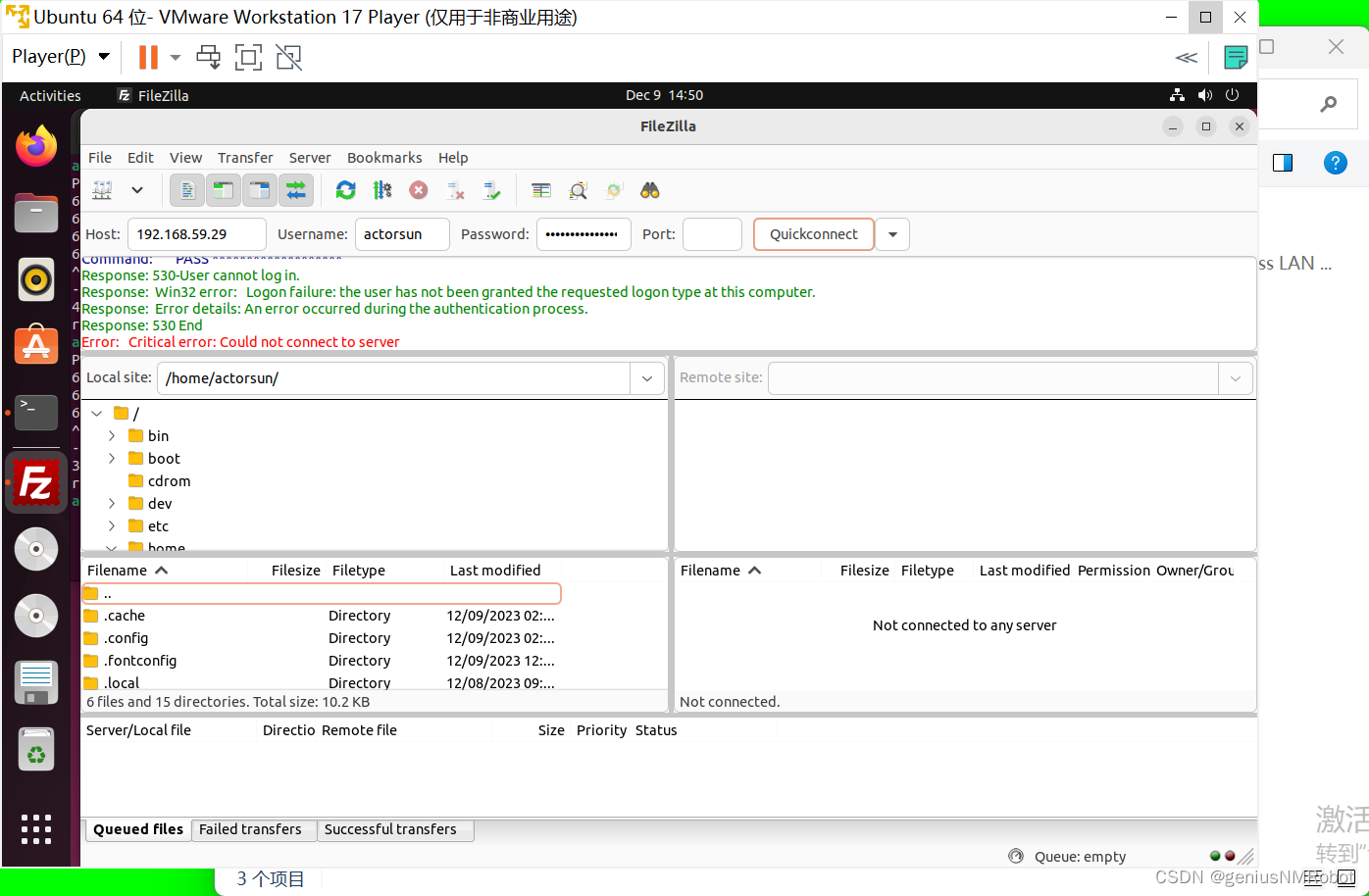
Ubuntu与Windows通讯传输文件(FTP服务器版)(没用的方法,无法施行)
本文介绍再Windows主机上建立FTP服务器,并且在Ubuntu虚拟机上面访问Windows上FTP服务器的方法 只要按照上图配置就可以了 第二部:打开IIS管理控制台 右击网站,新建FTP站点。需要注意的一点是在填写IP地址的时候,只需要填写Window…...
2024年AI视频识别技术的6大发展趋势预测
随着人工智能技术的快速发展,AI视频识别技术也将会得到进一步的发展和应用。2023年已经进入尾声,2024年即将来临,那么AI视频识别技术又将迎来怎样的发展趋势?本文将对2023年的AI视频技术做一个简单的盘点并对2024年的发展趋势进行…...

一篇文章了解JDK的前世今生
我们每天都在开发Java,每天都在使用JDK,那么我们了解JDK的发展史吗,这篇文章将带你深入了解JDK的发展史。 JDK(Java Development Kit)是Java开发者工具包,是用于编写Java程序和运行Java程序的软件开发工具集。自从1995年Java语言首次发布以来,JDK已经经历了数十年的发展…...

Redisson出现问题总结
org.redisson.client.RedisAuthRequiredException: NOAUTH Authentication required… channel: 出现此问题的原因为没有redis权限。解决方案在setAddress()后面加上setPassword()方法。 config.useSingleServer().setAddress("redis://localhost:6379").setPasswo…...

领域驱动架构(DDD)建模
一、背景 常见的软件开发方式是拿到产品需求后,直接考虑数据库中表应该如何设计,这种方式已经将设计与业务需求脱节,而更多的是直接考虑应该如何实现了,这有点本末倒置。而DDD是从领域(问题域)为出发点进行的设计方法。 领域驱动…...
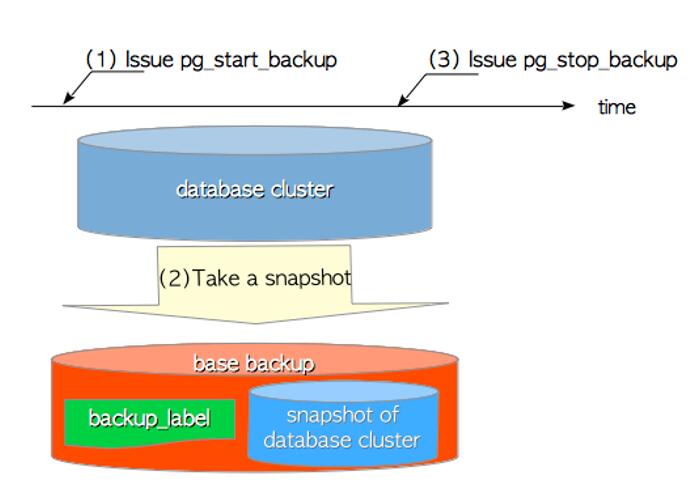
PostgreSQL从小白到高手教程 - 第38讲:数据库备份
PostgreSQL从小白到专家,是从入门逐渐能力提升的一个系列教程,内容包括对PG基础的认知、包括安装使用、包括角色权限、包括维护管理、、等内容,希望对热爱PG、学习PG的同学们有帮助,欢迎持续关注CUUG PG技术大讲堂。 第38讲&#…...
 和 eglCreateWindowSurface() 的对比和使用)
OpenGL ES eglCreatePbufferSurface() 和 eglCreateWindowSurface() 的对比和使用
一、介绍 相同点: eglCreatePbufferSurface 和 eglCreateWindowSurface 都是 OpenGL ES 中用于创建不同类型的EGL表面的函数,以便在OpenGL ES中进行渲染。 不同点: 选择使用哪种表面类型取决于你的需求。如果你只是需要在内存中进行离屏渲…...
)
python之马尔科夫链(Markov Chain)
马尔可夫链(Markov Chain)是一种随机过程,具有“马尔可夫性质”,即在给定当前状态的条件下,未来状态的概率分布仅依赖于当前状态,而与过去状态无关。马尔可夫链在很多领域都有广泛的应用,包括蒙…...
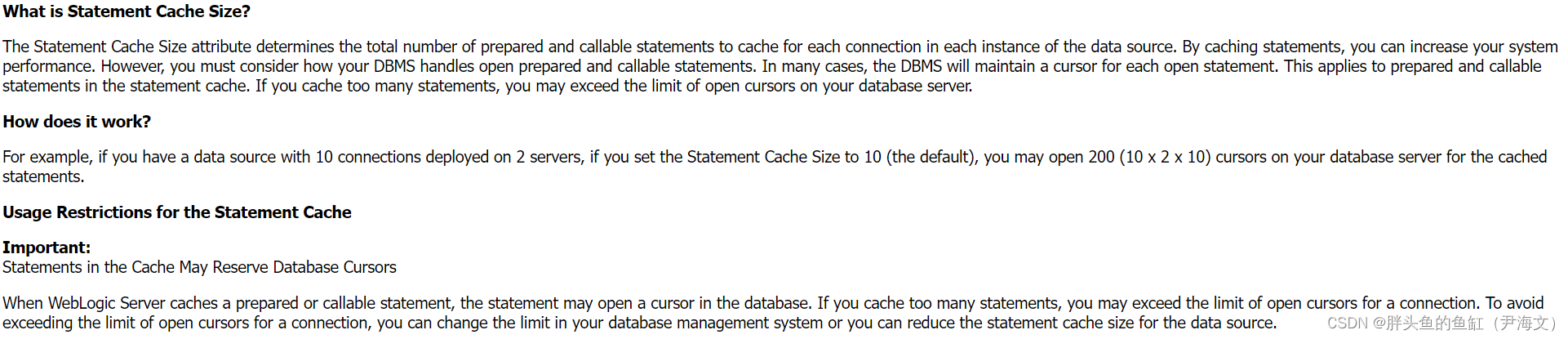
数据库管理-第123期 Oracle相关两个参数(202301205)
数据库管理-第123期 Oracle相关两个参数(202301205) 最近在群聊中看到俩和Oracle数据库相关的俩参数,一个是Oracle数据库本身的,一个是来自于Weblogic的,挺有趣的,本期研究一下。(本期涉及参数…...

掌握vue中国际化使用及配置
文章目录 🍁i18n组件安装🍁项目中配置 vue-i18n🍁编写语言包🍁国际化的使用 随着互联网的普及和全球化的发展,开发国际化的应用程序已经成为一种趋势。因此,将 VUE 应用程序国际化是非常有必要的。 以下是…...
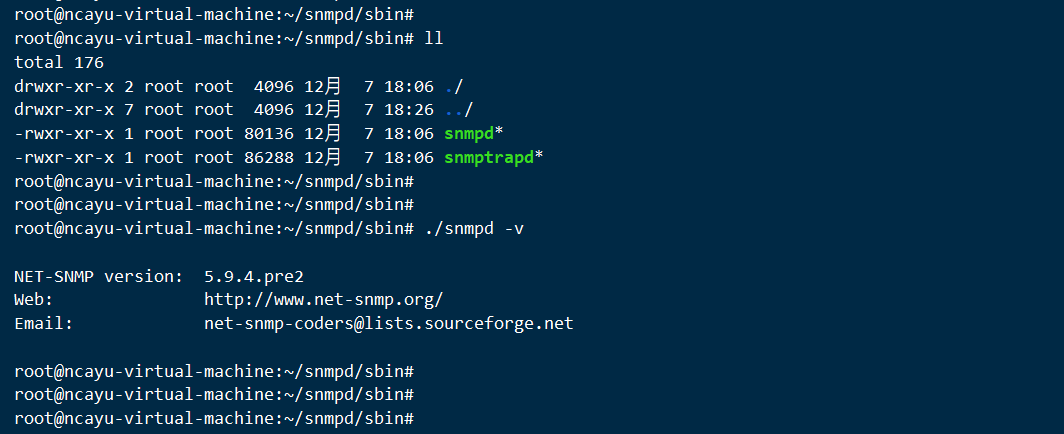
Ubuntu编译文件安装SNMP服务
net-snmp源码下载 http://www.net-snmp.org/download.html 编译步骤 指定参数编译 ./configure --prefix/root/snmpd --with-default-snmp-version"2" --with-logfile"/var/log/snmpd.log" --with-persistent-directory"/var/net-snmp" --wi…...
3D Web可视化平台助力Aras开发PLM系统:提供数据访问、可视化和发布功能
HOOPS中文网慧都科技是HOOPS全套产品中国地区指定授权经销商,提供3D软件开发工具HOOPS售卖、试用、中文试用指导服务、中文技术支持。http://techsoft3d.evget.com/ Aras是一个面向数字化工业应用的开放性平台,帮助世界领先的复杂互联产品制造商转变其产…...

Graphpad Prism10.1.0 安装教程 (含Win/Mac版)
GraphPad Prism GraphPad Prism是一款非常专业强大的科研医学生物数据处理绘图软件,它可以将科学图形、综合曲线拟合(非线性回归)、可理解的统计数据、数据组织结合在一起,除了最基本的数据统计分析外,还能自动生成统…...

【动态规划】路径问题_不同路径_C++
题目链接:leetcode不同路径 目录 题目解析: 算法原理 1.状态表示 2.状态转移方程 3.初始化 4.填表顺序 5.返回值 编写代码 题目解析: 题目让我们求总共有多少条不同的路径可到达右下角; 由题可得: 机器人位于…...
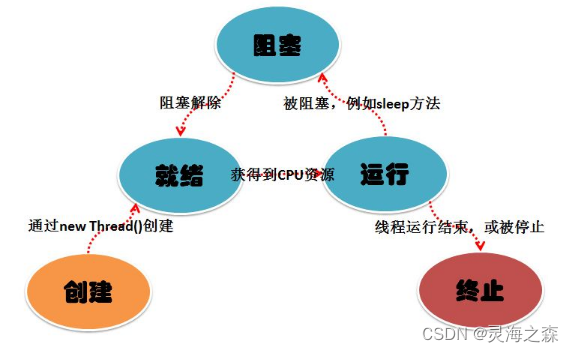
Python并发-线程和进程
一、线程和进程对应的问题 **1.进程:**CPU密集型也叫计算密集型,指的是系统的硬盘、内存性能相对CPU要好很多,此时,系统运作大部分的状况是CPU Loading 100%,CPU要读/写I/O(硬盘/内存),I/O在很短的时间就可…...

微信小程序适配方案:rpx(responsive pixel响应式像素单位)
小程序适配单位:rpx 规定任何屏幕下宽度为750rpx 小程序会根据屏幕的宽度自动计算rpx值的大小 Iphone6下:1rpx 1物理像素 0.5css 小程序编译后,rpx会做一次px换算,换算是以375个物理像素为基准,也就是在一个宽度…...
vue2 echarts饼状图,柱状图,折线图,简单封装以及使用
vue2 echarts饼状图,柱状图,折线图,简单封装以及使用 1. 直接上代码(复制可直接用,请根据自己的文件修改引用地址,图表只是简单封装,可根据自身功能,进行进一步配置。) …...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...
