机器学习之无监督学习:九大聚类算法
今天,和大家分享一下机器学习之无监督学习中的常见的聚类方法。
今天,和大家分享一下机器学习之无监督学习中的常见的聚类方法。
在无监督学习中,我们的数据并不带有任何标签,因此在无监督学习中要做的就是将这一系列无标签的数据输入到算法中,然后让算法找到一些隐含在数据中的结构,通过下图中的数据,可以找到的一个结构就是数据集中的点可以分成两组分开的点集(簇),能够圈出这些簇(cluster)的算法,就叫做聚类算法(clustering algorithm)。

聚类算法的应用

- 市场分割:将数据库中客户的信息根据市场进行不同的分组,从而实现对其分别销售或者根据不同的市场进行服务改进。
- 社交网络分析:通过邮件最频繁联系的人及其最频繁联系的人来找到一个关系密切的群体。
- 组织计算机集群:在数据中心里,计算机集群经常一起协同工作,可以用它来重新组织资源、重新布局网络、优化数据中心以及通信数据。
- 了解银河系的构成:利用这些信息来了解一些天文学的知识。
聚类分析的目标是将观测值划分为组(“簇”),以便分配到同一簇的观测值之间的成对差异往往小于不同簇中的观测值之间的差异。聚类算法分为三种不同的类型:组合算法、混合建模和模式搜索。
常见的几种聚类算法有:
- K-Means Clustering
- Hierarchical Clustering
- Agglomerative Clustering
- Affinity Propagation
- Mean Shift Clustering
- Bisecting K-Means
- DBSCAN
- OPTICS
- BIRCH
K-means
K-means 算法是目前最流行的聚类方法之一。
K-means 是由贝尔实验室的 Stuart Lloyd 在 1957 年提出来的,最开始是用于脉冲编码调制,直到 1982 年才将该算法对外公布。1965 年,Edward W.Forgy 发布了相同的算法,因此 K-Means 有时被称为 Lloyd-Forgy。
在聚类问题中,我们会给定一组未加标签的数据集,同时希望有一个算法能够自动地将这些数据分成有紧密关系的的(coherent)子集(subsets) 或是簇(clusters)。K 均值(K-means)算法是现在最热门最为广泛运用的聚类算法。
直观理解 K 均值算法:

假如有一个无标签的数据集(上图左),并且我们想要将其分为两个簇,现在执行 K 均值算法,具体操作如下:
- 第一步,随机生成两个点(因为想要将数据聚成两类)(上图右),这两个点叫做聚类中心(cluster centroids)。
- 第二步,进行 K 均值算法的内循环。K 均值算法是一个迭代算法,它会做两件事情,第一个是簇分配(cluster assignment),第二个是移动聚类中心(move centroid)。
内循环的第一步是要进行簇分配,也就是说,遍历每一个样本,再根据每一个点到聚类中心距离的远近将其分配给不同的聚类中心(离谁近分配给谁),对于本例而言,就是遍历数据集,将每个点染成红色或蓝色。
内循环的第二步是移动聚类中心,将红色和蓝色的聚类中心移动到各自点的均值处(每组点的平均位置)。
接着就是将所有的点根据与新的聚类中心距离的远近进行新的簇分配,如此循环,直至聚类中心的位置不再随着迭代而改变,并且点的颜色也不再发生改变,此时可以说 K 均值已经聚合了。该算法在找出数据中两个簇的方面做的相当好。

K-Means算法的优点:
简单易懂,计算速度较快,适用于大规模数据集。
缺点:
- 例如对于非球形簇的处理能力较差,容易受到初始簇心的选择影响,需要预先指定簇的数量K等。
- 此外,当数据点之间存在噪声或者离群点时,K-Means算法可能会将它们分配到错误的簇中。
Hierarchical Clustering
层次聚类(Hierarchical Clustering)顾名思义就是按照某个层次对样本集进行聚类操作,这里的层次实际上指的就是某种距离定义。
层次聚类最终的目的是消减类别的数量,所以在行为上类似于树状图由叶节点逐步向根节点靠近的过程,这种行为过程又被称为“自底向上”。
更通俗的,层次聚类是将初始化的多个类簇看做树节点,每一步迭代,都是将两两相近的类簇合并成一个新的大类簇,如此反复,直至最终只剩一个类簇(根节点)。
层次聚类策略分为两种基本范式:聚集型(自下而上)和分裂型(自上而下)。
与层次聚类相反的是分裂聚类(divisive clustering),又名 DIANA(Divise Analysis),它的行为过程为“自顶向下”。
应用 K-means 的结果取决于要搜索的聚类数量的选择和起始配置分配。相反,层次聚类方法不需要这样的规范。相反,它们要求用户根据两组观察值之间的成对差异性,指定(不相交)观察组之间的差异性度量。顾名思义,它们产生层次结构表示,其中层次结构每个级别的集群都是通过合并下一个较低级别的集群来创建的。在最低级别,每个集群包含一个观察值。在最高级别,只有一个集群包含所有数据。
优点:
- 距离和规则的相似度容易定义,限制少;
- 不需要预先制定聚类数;
- 可以发现类的层次关系;
- 可以聚类成其它形状。
缺点:
- 计算复杂度太高;
- 奇异值也能产生很大影响;
- 算法很可能聚类成链状。
Agglomerative Clustering
凝聚层次聚类(Agglomerative Clustering)是一种自底向上的聚类算法,它将每个数据点视为一个初始簇,并将它们逐步合并成更大的簇,直到达到停止条件为止。在该算法中,每个数据点最初被视为一个单独的簇,然后逐步合并簇,直到所有数据点被合并为一个大簇。
优点:
- 适用于不同形状和大小的簇,且不需要事先指定聚类数目。
- 该算法也可以输出聚类层次结构,便于分析和可视化。
缺点:
- 计算复杂度较高,尤其是在处理大规模数据集时,需要消耗大量的计算资源和存储空间。
- 该算法对初始簇的选择也比较敏感,可能会导致不同的聚类结果。
Affinity Propagation
Affinity Propagation(AP)算法,通常被翻译为近邻传播算法或者亲和力传播算法,
Affinity Propagation 是一种基于图论的聚类算法,旨在识别数据中的"exemplars"(代表点)和"clusters"(簇)。与 K-Means 等传统聚类算法不同,Affinity Propagation 不需要事先指定聚类数目,也不需要随机初始化簇心,而是通过计算数据点之间的相似性得出最终的聚类结果。
优点:
- 不需要制定最终聚类族的个数
- 已有的数据点作为最终的聚类中心,而不是新生成一个簇中心。
- 模型对数据的初始值不敏感。
- 对初始相似度矩阵数据的对称性没有要求。
- 相比与 k-centers 聚类方法,其结果的平方差误差较小。
缺点:
- 该算法的计算复杂度较高,需要大量的存储空间和计算资源;
- 对于噪声点和离群点的处理能力较弱。
Mean Shift Clustering
Mean Shift Clustering 是一种基于密度的非参数聚类算法,其基本思想是通过寻找数据点密度最大的位置(称为"局部最大值"或"高峰"),来识别数据中的簇。算法的核心是通过对每个数据点进行局部密度估计,并将密度估计的结果用于计算数据点移动的方向和距离。算法的核心是通过对每个数据点进行局部密度估计,并将密度估计的结果用于计算数据点移动的方向和距离。
优点:
- 不需要指定簇的数目,且对于形状复杂的簇也有很好的效果。
- 算法还能够有效地处理噪声数据。
缺点:
- 计算复杂度较高,尤其是在处理大规模数据集时,需要消耗大量的计算资源和存储空间;
- 该算法还对初始参数的选择比较敏感,需要进行参数调整和优化。
Bisecting K-Means
Bisecting K-Means 是一种基于 K-Means 算法的层次聚类算法,其基本思想是将所有数据点划分为一个簇,然后将该簇分成两个子簇,并对每个子簇分别应用 K-Means 算法,重复执行这个过程,直到达到预定的聚类数目为止。
算法首先将所有数据点视为一个初始簇,然后对该簇应用K-Means算法,将该簇分成两个子簇,并计算每个子簇的误差平方和(SSE)。然后,选择误差平方和最大的子簇,并将其再次分成两个子簇,重复执行这个过程,直到达到预定的聚类数目为止。
优点:
- 具有较高的准确性和稳定性,能够有效地处理大规模数据集,并且不需要指定初始聚类数目。
- 该算法还能够输出聚类层次结构,便于分析和可视化。
缺点:
- 计算复杂度较高,尤其是在处理大规模数据集时,需要消耗大量的计算资源和存储空间。
- 此外该算法对初始簇的选择也比较敏感,可能会导致不同的聚类结果。
DBSCAN
具有噪声的基于密度的聚类方法(Density-Based Spatial Clustering of Applications with Noise,DBSCAN)是一种典型的基于密度的空间聚类算法。
基于密度的方法的特点是不依赖于距离,而是依赖于密度,从而克服基于距离的算法只能发现“球形”聚簇的缺点。
DBSCAN算法的核心思想是:对于一个给定的数据点,如果它的密度达到一定的阈值,则它属于一个簇中;否则,它被视为噪声点。
优点:
- 这类算法能克服基于距离的算法只能发现“类圆形”(凸)的聚类的缺点;
- 可发现任意形状的聚类,且对噪声数据不敏感;
- 不需要指定类的数目 cluster;
- 算法中只有两个参数,扫描半径 (eps)和最小包含点数(min_samples)。
缺点:
- 计算复杂度,不进行任何优化时,算法的时间复杂度是O(N^{2}),通常可利用R-tree,k-d tree, ball;
- tree索引来加速计算,将算法的时间复杂度降为O(Nlog(N));
- 受eps影响较大。在类中的数据分布密度不均匀时,eps较小时,密度小的cluster会被划分成多个性质相似的cluster;eps较大时,会使得距离较近且密度较大的cluster被合并成一个cluster。在高维数据时,因为维数灾难问题,eps的选取比较困难;
- 依赖距离公式的选取,由于维度灾害,距离的度量标准不重要;
- 不适合数据集集中密度差异很大的,因为eps和metric选取很困难。
OPTICS
OPTICS(Ordering Points To Identify the Clustering Structure)是一种基于密度的聚类算法,其能够自动确定簇的数量,同时也可以发现任意形状的簇,并能够处理噪声数据。
OPTICS 算法的核心思想是:对于一个给定的数据点,通过计算它到其它点的距离,确定其在密度上的可达性,从而构建一个基于密度的距离图。然后,通过扫描该距离图,自动确定簇的数量,并对每个簇进行划分。
优点:
- 能够自动确定簇的数量,并能够处理任意形状的簇,并能够有效地处理噪声数据。
- 该算法还能够输出聚类层次结构,便于分析和可视化。
缺点:
- 计算复杂度较高,尤其是在处理大规模数据集时,需要消耗大量的计算资源和存储空间。
- 该算法对于密度差异较大的数据集,可能会导致聚类效果不佳。
BIRCH
BIRCH(Balanced Iterative Reducing and Clustering using Hierarchies)是一种基于层次聚类的聚类算法,其可以快速地处理大规模数据集,并且对于任意形状的簇都有较好的效果。
BIRCH算法的核心思想是:通过对数据集进行分级聚类,逐步减小数据规模,最终得到簇结构。BIRCH算法采用一种类似于B树的结构,称为CF树,它可以快速地插入和删除子簇,并且可以自动平衡,从而确保簇的质量和效率。
优点:
- 能够快速处理大规模数据集,并且对于任意形状的簇都有较好的效果。
- 该算法对于噪声数据和离群点也有较好的容错性。
缺点:
- 对于密度差异较大的数据集,可能会导致聚类效果不佳;
- 对于高维数据集的效果也不如其他算法。
相关文章:

机器学习之无监督学习:九大聚类算法
今天,和大家分享一下机器学习之无监督学习中的常见的聚类方法。 今天,和大家分享一下机器学习之无监督学习中的常见的聚类方法。 在无监督学习中,我们的数据并不带有任何标签,因此在无监督学习中要做的就是将这一系列无标签的数…...
Linux高级管理-搭建网站服务
在Ihternet 网络环境中,Web 服务无疑是最为流行的应用系统。有了Web站点,企业可以充分 展示自己的产品,宣传企业形象。Web站点还为企业提供了与客户交流、电子商务交易平台等丰富 的网络应用。部署与维护Web 服务是运维工程师必须掌握的一个技…...
Windows 系统,TortoiseSVN 无法修改 Log 信息解决方法
使用SVN提交版本信息时,注释内容写的不全。通过右键TortoiseSVN的Show log看到提交的的注释,右键看到Edit log message的选项,然而提交后却给出错误提示: Repository has not been enabled to accept revision propchanges; ask …...

编译 Android gradle-4.6-all.zip 报错问题记录
编译 Android gradle-4.6-all.zip 报错问题记录 方法一:替换资源:方法二:修改源方法三:修改版本 编译时候无法下载 gradle-4.6-all Downloading https://services.gradle.org/distributions/gradle-4.6-all.zip 方法一…...
Linux系统调试课:Valgrind 内存调试
文章目录 一、为什么要学会Valgrind二、什么是内存泄露三、Valgrind的移植四、Valgrind相关参数沉淀、分享、成长,让自己和他人都能有所收获!😄 📢Valgrind 是一个开源的内存调试和性能分析工具,用于帮助开发者找出程序中的内存错误,如内存泄漏、使用未初始化的内存、非…...

python主流开发工具排名,python开发工具有哪些
本篇文章给大家谈谈python的开发工具软件有哪些,以及python主流开发工具排名,希望对各位有所帮助,不要忘了收藏本站喔。 python中用到哪些软件 一、Python代码编辑器1、sublime Textsublime Text是一款非常流行的代码编辑器,支持P…...
Spring Boot Async:从入门到精通,原理详解与最佳实践
Spring Boot 的异步功能(Async)允许我们将某些任务异步执行,而不会阻塞主线程。这对于处理耗时的操作非常有用,如发送电子邮件、生成报表、调用外部 API 等。通过异步处理,我们可以释放主线程,让它继续处理…...

oracle 19c创建db_link名称带.com域名问题处理
文章目录 一、修改PDB的global_name二、重启数据库实例三、修改domain后重试 一、修改PDB的global_name SYSorcl1>sho pdbsCON_ID CON_NAME OPEN MODE RESTRICTED ---------- ------------------------------ ---------- ----------2 PDB$SEED …...

银行卡二要素API的应用案例:从在线购物到金融投资
引言 随着互联网技术的不断发展,人们的金融需求也在不断增加。随之而来的是各种新型金融服务的涌现,让用户的金融体验更加便利快捷。其中,银行卡二要素API的应用,则为用户的金融体验和安全性提供了极大的保障。 银行卡二要素API…...
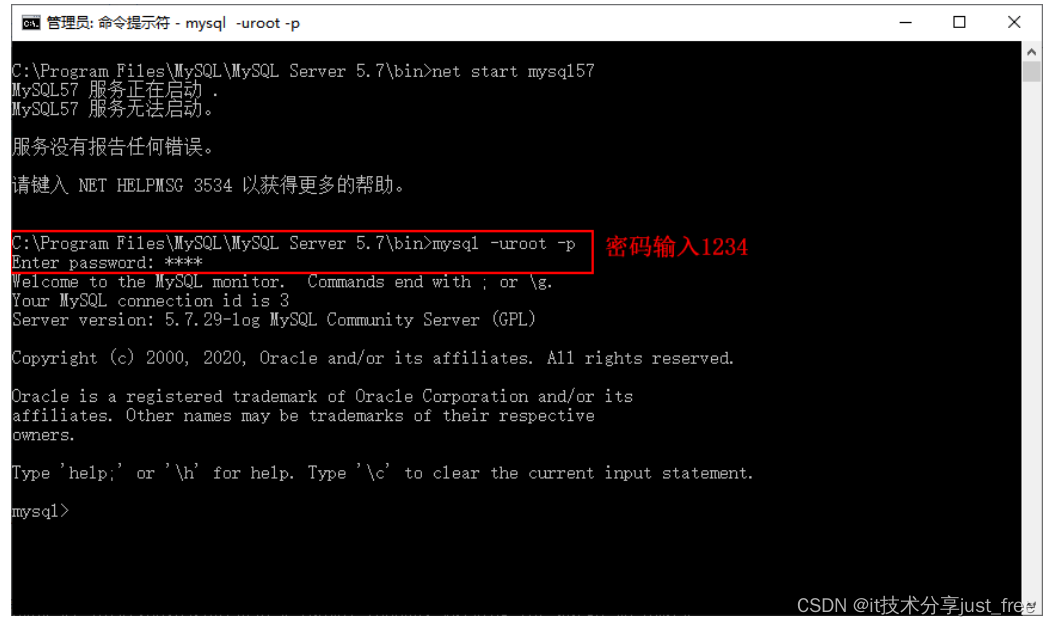
MySQL 忘记root密码后重置密码操作
在忘记 MySQL 密码的情况下,可以通过 --skip-grant-tables 关闭服务器的认证,然后重置 root 的密码,具体操作步骤如下。 步骤 1):关闭正在运行的 MySQL 服务。打开 cmd 进入 MySQL 的 bin 目录。 步骤 2):输入mysqld -…...
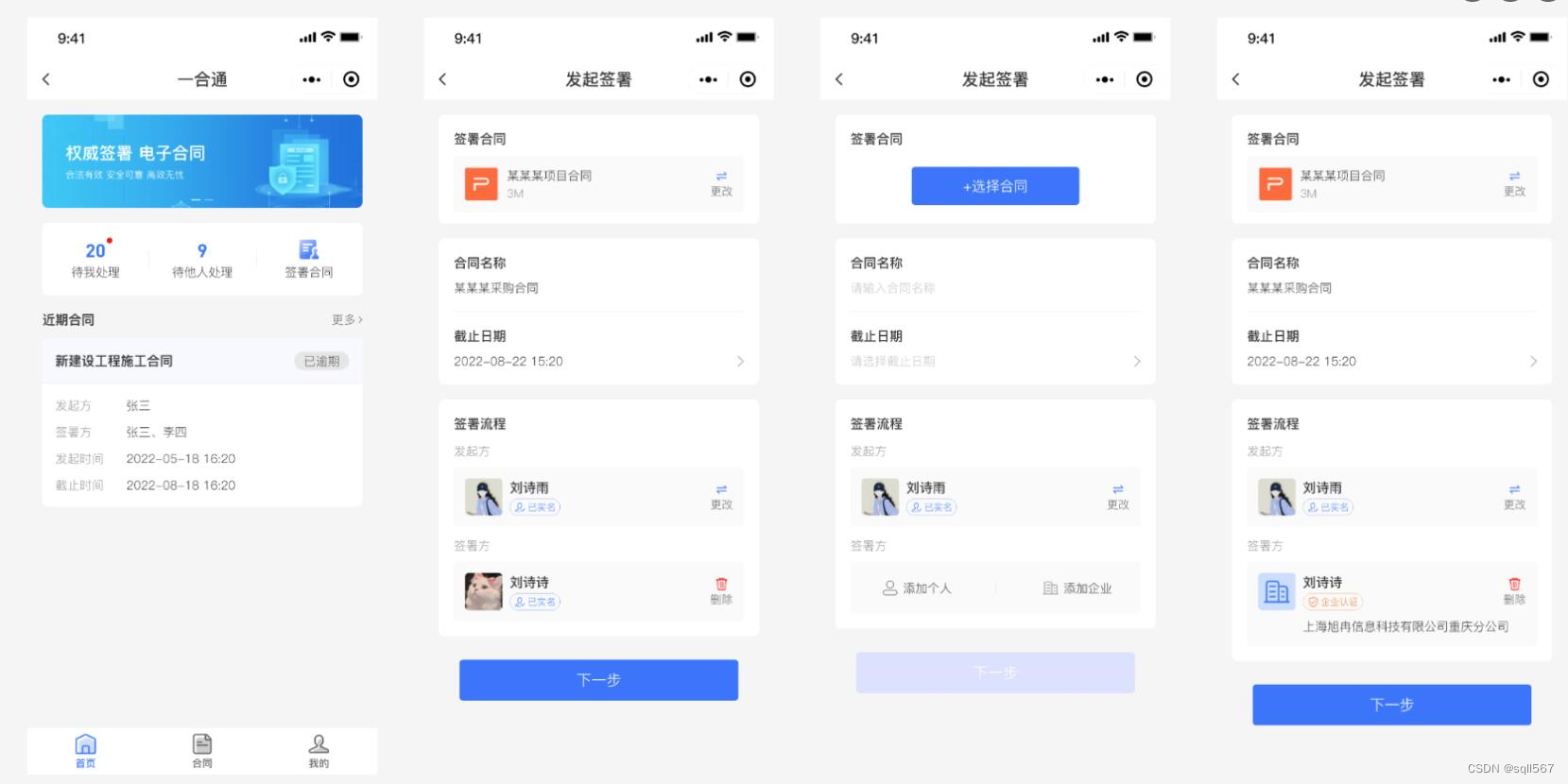
开源电子合同签署平台小程序源码/电子文件签字+在线合同签署系统源码/电子合同小程序源码
源码简介: 开源电子合同签署平台小程序源码,它是电子文件签字在线合同签署系统源码/电子合同小程序源码 目前商业端和开源端一致,免费开源状态! 聚合市场上各类电子合同解决方案商,你无需一个一个的对接电子合同厂商…...

J.408之数据结构
J-408之数据结构_北京信息科技大学第十五届程序设计竞赛(同步赛) (nowcoder.com) 思维好题,直接用两个set存没出现的数字就好了 // Problem: 408之数据结构 // Contest: NowCoder // URL: https://ac.nowcoder.com/acm/contest/68572/J // Me…...

前端食堂技术周刊第 107 期:技术播客节、Deno Cron、FEDAY、XState v5、Electron 2023 生态系统回顾
美味值:🌟🌟🌟🌟🌟 口味:烤椰拿铁 食堂技术周刊仓库地址:https://github.com/Geekhyt/weekly 大家好,我是童欧巴。欢迎来到前端食堂技术周刊,我们先来看下…...

三防平板|手持终端PDA|8寸/10寸工业三防平板电脑主板方案定制
近年来,随着科技的快速发展,三防平板成为了各行各业中不可或缺的工具。三防平板采用IP67级别的防护设计,通过了多项测试标准,如国标和美标,具备防水、防摔、防尘、防撞、防震、防跌落以及防盐雾等多重防护功能。因此&a…...
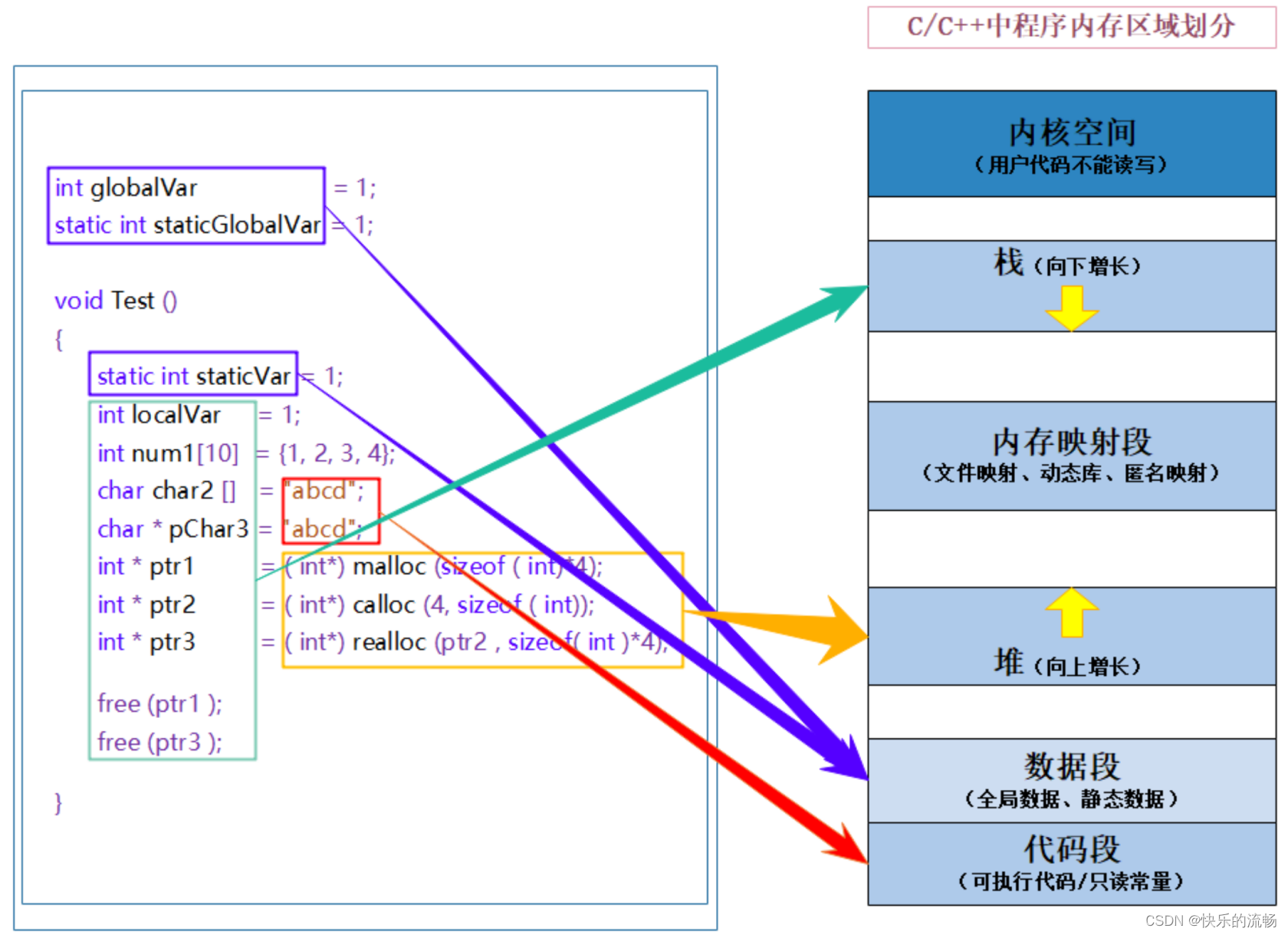
【C语言】动态内存管理(C语言的难点与精华,数据结构的前置知识,你真的掌握了吗?)
文章目录 引言一、为什么要动态内存分配二、动态内存分配的相关函数2.1 malloc2.2 free2.3 calloc2.4 realloc 三、常见的动态内存的错误3.1 对NULL指针的解引用3.2 对动态内存越界访问3.3 对非动态内存释放3.4 对动态内存部分释放3.5 对动态内存多次释放3.6 未对动态内存释放&…...
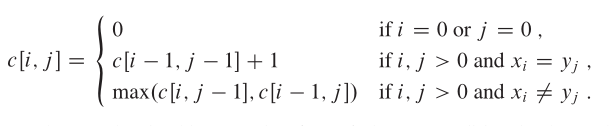
最长子序列问题(LCS)--动态规划解法
题目描述: 如果Z既是X的子序列,又是Y的子序列,则称Z为X和Y的公共子序列。 如果给定X、Y,求出Y及其长度。 示例: 输入 ABCPDSFJGODIHJOFDIUSHGD OSDIHGKODGHBLKSJBHKAGHI 输出 SDIHODSHG 9 分析: c…...

实时流式计算 kafkaStream
文章目录 实时流式计算Kafka StreamKafka Streams 的关键概念KStreamKafka Stream入门案例编写SpringBoot 集成 Kafka Stream 实时流式计算 一般流式计算会与批量计算相比较 流式计算就相当于上图的右侧扶梯,是可以源源不断的产生数据,源源不断的接收数…...

西南科技大学模拟电子技术实验七(集成运算放大器的非线性应用)预习报告
一、计算/设计过程 说明:本实验是验证性实验,计算预测验证结果。是设计性实验一定要从系统指标计算出元件参数过程,越详细越好。用公式输入法完成相关公式内容,不得贴手写图片。(注意:从抽象公式直接得出结果,不得分,页数可根据内容调整) 预习计算内容根据运放的非线…...
Ubuntu与Windows通讯传输文件(FTP服务器版)(没用的方法,无法施行)
本文介绍再Windows主机上建立FTP服务器,并且在Ubuntu虚拟机上面访问Windows上FTP服务器的方法 只要按照上图配置就可以了 第二部:打开IIS管理控制台 右击网站,新建FTP站点。需要注意的一点是在填写IP地址的时候,只需要填写Window…...
2024年AI视频识别技术的6大发展趋势预测
随着人工智能技术的快速发展,AI视频识别技术也将会得到进一步的发展和应用。2023年已经进入尾声,2024年即将来临,那么AI视频识别技术又将迎来怎样的发展趋势?本文将对2023年的AI视频技术做一个简单的盘点并对2024年的发展趋势进行…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

Kubernetes 网络模型深度解析:Pod IP 与 Service 的负载均衡机制,Service到底是什么?
Pod IP 的本质与特性 Pod IP 的定位 纯端点地址:Pod IP 是分配给 Pod 网络命名空间的真实 IP 地址(如 10.244.1.2)无特殊名称:在 Kubernetes 中,它通常被称为 “Pod IP” 或 “容器 IP”生命周期:与 Pod …...

负载均衡器》》LVS、Nginx、HAproxy 区别
虚拟主机 先4,后7...

命令行关闭Windows防火墙
命令行关闭Windows防火墙 引言一、防火墙:被低估的"智能安检员"二、优先尝试!90%问题无需关闭防火墙方案1:程序白名单(解决软件误拦截)方案2:开放特定端口(解决网游/开发端口不通)三、命令行极速关闭方案方法一:PowerShell(推荐Win10/11)方法二:CMD命令…...
