TinyMPC - CMU (卡耐基梅隆大学)开源的机器人 MPC 控制器
系列文章目录
CasADi - 最优控制开源 Python/MATLAB 库
文章目录
- 系列文章目录
- 前言
- 一、机器人硬件对比
- 1.1 Teensy 上的微控制器基准测试
- 1.2 机器人硬件
- 1.3 BibTeX
- 二、求解器
- 三、功能(预期)
- 3.1 高效
- 3.2 鲁棒
- 3.3 可嵌入式
- 3.4 最小依赖性
- 3.5 高效热启动
- 3.6 接口
- 四、在 Ubuntu 安装
- 4.1 在终端克隆此 repo
- 4.2 导航至根目录并运行
- 4.3 执行 CMake 配置步骤
- 4.4 构建 TinyMPC
- 五、示例
- 5.1 运行四旋翼飞行器悬停示例
- 5.2 运行 codegen 示例,然后在该目录下按照相同的构建步骤进行操作
前言
TinyMPC: 资源受限微控制器上的模型预测控制
作者:Anoushka Alavilli*, Khai Nguyen*, Sam Schoedel*, Brian Plancher, Zachary Manchester
Carnegie Mellon University, Barnard College
模型预测控制(Model-predictive control,MPC)是控制受复杂约束条件(complex constraints)影响的高动态机器人系统(highly dynamic robotic systems)的有力工具。然而,MPC 的计算要求很高,在资源有限的小型机器人平台上实施往往不切实际。我们推出的 TinyMPC 是一种高速 MPC 求解器,内存占用少,适用于小型机器人上常见的微控制器。我们的方法基于交替方向乘子法(ADMM),并利用 MPC 问题的结构来提高效率。我们以最先进的求解器 OSQP 为基准,对 TinyMPC 进行了演示,速度提高了近一个数量级,同时还在一个重达 27 克的四旋翼机器人上进行了硬件实验,演示了高速轨迹跟踪(high-speed trajectory tracking)和动态避障(dynamic obstacle avoidance)。
一、机器人硬件对比
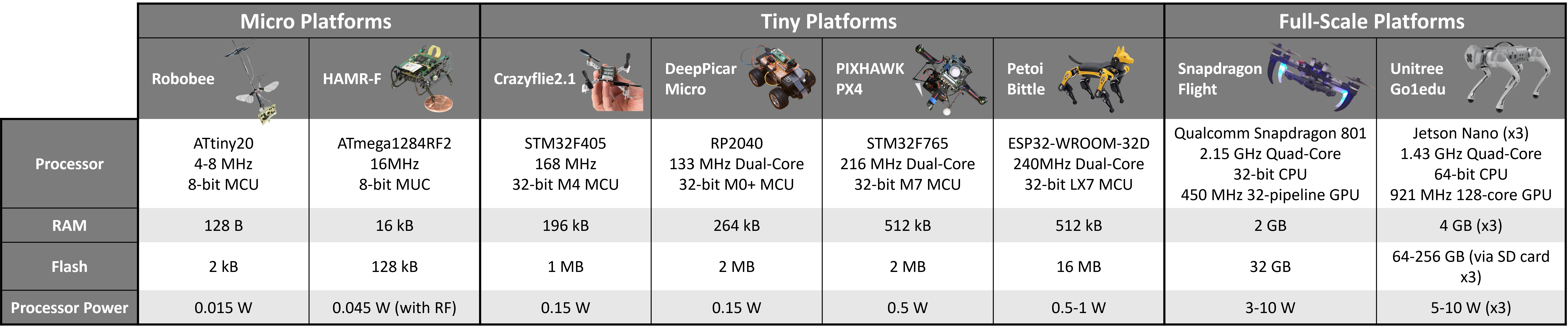

1.1 Teensy 上的微控制器基准测试
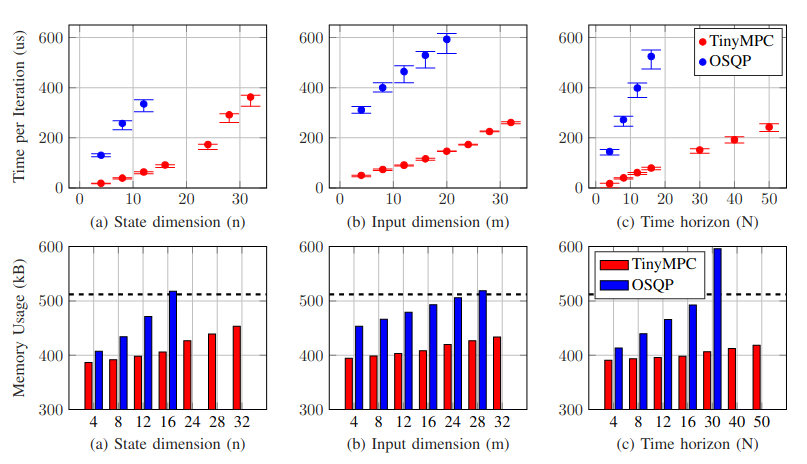
1.2 机器人硬件

1.3 BibTeX
@misc{tinympc,title={TinyMPC: Model-Predictive Control on Resource-Constrained Microcontrollers}, author={Anoushka Alavilli and Khai Nguyen and Sam Schoedel and Brian Plancher and Zachary Manchester},year={2023},eprint={2310.16985},archivePrefix={arXiv},primaryClass={cs.RO}
}二、求解器
TinyMPC 求解器是一个数值优化软件包,用于求解默认形式的凸二次规划型模型预测控制(convex quadratic model-predictive control)
minimize: 1 2 ( x N − x ˉ N ) T Q f ( x N − x ˉ N ) + ∑ k = 0 N ( 1 2 ( x k − x ˉ k ) T Q ( x k − x ˉ k ) + 1 2 ( u k − u ˉ k ) T R ( u k − u ˉ k ) ) subject to: x k + 1 = A x k + B u k u ‾ ≤ u k ≤ u ‾ x ‾ ≤ x k ≤ x ‾ \begin{array}{l l}{\operatorname*{minimize:}}&{\dfrac{1}{2}(x_{N}-\bar{x}_{N})^{T}Q_{f}(x_{N}-\bar{x}_{N})+{{\sum_{k=0}^{N}\bigl(\frac{1}{2}(x_{k}-\bar{x}_{k})^{T}Q(x_{k}-\bar{x}_{k})+\frac{1}{2}\bigl(u_{k}-\bar{u}_{k}\bigr)^{T}R(u_{k}-\bar{u}_{k})\bigr)}}} \\ {\operatorname*{subject\;to:}}&x_{k+1}=A x_{k}+B u_{k} \\ & \overline{{{u}}}\,\leq\,u_{k}\,\leq\underline{{u}} \\ & \overline{{{x}}}\,\leq\,x_{k}\,\leq\underline{{x}} \end{array} minimize:subjectto:21(xN−xˉN)TQf(xN−xˉN)+∑k=0N(21(xk−xˉk)TQ(xk−xˉk)+21(uk−uˉk)TR(uk−uˉk))xk+1=Axk+Buku≤uk≤ux≤xk≤x
其中, x k ∈ R n x_{k}\in\mathbb{R}^{n} xk∈Rn、 u k ∈ R m u_{k}\in\mathbb{R}^{m} uk∈Rm 分别为时间步长为 k 时的状态和控制输入,N 为时间步长(也称为视平线), A ∈ R n × n A\in\mathbb{R}^{n\times n} A∈Rn×n 和 B ∈ R n × m B\in\mathbb{R}^{n\times m} B∈Rn×m 定义了系统动力学, Q ≥ 0 Q\geq0 Q≥0、 R ≻ 0 R\succ0 R≻0 和 Q f ≥ 0 Q_{f}\geq0 Qf≥0 为对称成本权重矩阵, x ~ k {\tilde{x}}_{k} x~k 和 u ˉ k {\bar{u}}_{k} uˉk 是状态和输入参考轨迹。
三、功能(预期)
3.1 高效
它采用基于 ADMM 的定制一阶方法,无需矩阵因式分解。所有其他操作都非常简单。它还利用 MPC 问题中的结构,为基元更新实现了黎卡提递归(Riccati recursion)。
3.2 鲁棒
该算法完全 free,而且不需要对问题数据做任何假设(问题只需要是凸的)。它就是这么简单!
3.3 可嵌入式
它有一个简单的接口,无需内存管理器即可生成定制的可嵌入 C 代码。
3.4 最小依赖性
它只需要 Eigen 就能运行。
3.5 高效热启动
它可以轻松热启动,并且可以缓存矩阵因式分解,从而极其高效地解决参数化问题。
3.6 接口
它为 C、C++、Julia、Matlab 和 Python 提供了接口。
四、在 Ubuntu 安装
4.1 在终端克隆此 repo
git clone git@github.com:TinyMPC/TinyMPC.git
4.2 导航至根目录并运行
cd TinyMPC
mkdir build && cd build
4.3 执行 CMake 配置步骤
cmake ../
4.4 构建 TinyMPC
make
五、示例
5.1 运行四旋翼飞行器悬停示例
./examples/example_quadrotor_hovering
tracking error at step 0: 2.2472
tracking error at step 1: 2.9549
tracking error at step 2: 2.5478
tracking error at step 3: 2.6331
tracking error at step 4: 3.1375
tracking error at step 5: 3.6413
tracking error at step 6: 4.0214
tracking error at step 7: 4.2898
tracking error at step 8: 4.5070
tracking error at step 9: 4.6282
tracking error at step 10: 4.3689
tracking error at step 11: 3.8895
tracking error at step 12: 3.3699
tracking error at step 13: 2.8681
tracking error at step 14: 2.3877
tracking error at step 15: 1.9336
tracking error at step 16: 1.5516
tracking error at step 17: 1.2588
tracking error at step 18: 1.0420
tracking error at step 19: 0.8844
tracking error at step 20: 0.7680
tracking error at step 21: 0.6773
tracking error at step 22: 0.6009
tracking error at step 23: 0.5316
tracking error at step 24: 0.4658
tracking error at step 25: 0.4024
tracking error at step 26: 0.3416
tracking error at step 27: 0.2839
tracking error at step 28: 0.2305
tracking error at step 29: 0.1822
tracking error at step 30: 0.1393
tracking error at step 31: 0.1023
tracking error at step 32: 0.0715
tracking error at step 33: 0.0472
tracking error at step 34: 0.0301
tracking error at step 35: 0.0217
tracking error at step 36: 0.0218
tracking error at step 37: 0.0251
tracking error at step 38: 0.0279
tracking error at step 39: 0.0291
tracking error at step 40: 0.0290
tracking error at step 41: 0.0277
tracking error at step 42: 0.0254
tracking error at step 43: 0.0227
tracking error at step 44: 0.0197
tracking error at step 45: 0.0167
tracking error at step 46: 0.0140
tracking error at step 47: 0.0116
tracking error at step 48: 0.0097
tracking error at step 49: 0.0082
tracking error at step 50: 0.0072
tracking error at step 51: 0.0067
tracking error at step 52: 0.0065
tracking error at step 53: 0.0065
tracking error at step 54: 0.0065
tracking error at step 55: 0.0064
tracking error at step 56: 0.0063
tracking error at step 57: 0.0062
tracking error at step 58: 0.0061
tracking error at step 59: 0.0059
tracking error at step 60: 0.0058
tracking error at step 61: 0.0056
tracking error at step 62: 0.0055
tracking error at step 63: 0.0054
tracking error at step 64: 0.0053
tracking error at step 65: 0.0052
tracking error at step 66: 0.0052
tracking error at step 67: 0.0052
tracking error at step 68: 0.0052
tracking error at step 69: 0.0052
5.2 运行 codegen 示例,然后在该目录下按照相同的构建步骤进行操作
./examples/example_codegen
A = [1, 1]
[5, 2]
B = [3, 4]
[3, 1]
Q = [1.1, 0]
[ 0, 1.1]
R = [2.1, 0]
[ 0, 2.1]
rho = 0.1
Kinf converged after 5 iterations
Precomputing finished
Kinf = [ 1.36, 0.5335]
[-0.6323, -0.1066]
Pinf = [8.899, 2.664]
[2.664, 2.046]
Quu_inv = [ 0.1076, -0.09799]
[-0.09799, 0.09522]
AmBKt = [-0.5502, 1.553]
[-0.1739, 0.5062]
coeff_d2p = [7.438e-06, 8.381e-06]
[2.127e-06, 2.398e-06]
Creating generated code directory at /home/khai/SSD/Code/TinyMPC/generated_code
ERROR OPENING DATA WORKSPACE FILE
Segmentation fault
相关文章:

TinyMPC - CMU (卡耐基梅隆大学)开源的机器人 MPC 控制器
系列文章目录 CasADi - 最优控制开源 Python/MATLAB 库 文章目录 系列文章目录前言一、机器人硬件对比1.1 Teensy 上的微控制器基准测试1.2 机器人硬件1.3 BibTeX 二、求解器三、功能(预期)3.1 高效3.2 鲁棒3.3 可嵌入式3.4 最小依赖性3.5 高效热启动3.…...

C++ 对象的初始化和清理:构造函数和析构函数
目录 构造函数和析构函数 构造函数 析构函数 构造函数的分类及调用 括号法 显示法 隐式转换法 拷贝构造函数的调用时机 使用一个已经创建完毕的对象来初始化一个新对象 值传递的方式给函数参数传值 以值方式返回局部对象 构造函数调用规则 初始化列表 类对象作…...

Tmux中使用Docker报错 - 解决方案
问题 进入Tmux会话后,在其中使用Docker可能会出现如下报错: Got permission denied while trying to connect to the Docker ……解决方案 退出tmux会话: tmux detach在tmux会话外部杀掉tmux进程: pkill -f tmux重新进入tmux:…...

如何在WordPress中批量替换图片路径?
很多站长在使用WordPress博客或者搬家时,需要把WordPress文章中的图片路径进行替换来解决图片不显示的问题。总结一下WordPress图片路径批量替换的过程,方便有此类需求的站长们学习。 什么情况下批量替换图片路径 1、更换了网站域名 有许多网站建设初期…...
el-pagination 纯前端分页
需求:后端把所有数据都返给前端,前端进行分页渲染。 实现思路:先把数据存储到一个大数组中,然后调用方法进行切割。主要使用数组的slice方法 所有代码: html <template><div style"padding: 20px&qu…...
基于springboot的校园二手市场
博主主页:猫头鹰源码 博主简介:Java领域优质创作者、CSDN博客专家、公司架构师、全网粉丝5万、专注Java技术领域和毕业设计项目实战 主要内容:毕业设计(Javaweb项目|小程序等)、简历模板、学习资料、面试题库、技术咨询 文末联系获取 项目介绍…...

【开源】基于Vue和SpringBoot的在线课程教学系统
项目编号: S 014 ,文末获取源码。 \color{red}{项目编号:S014,文末获取源码。} 项目编号:S014,文末获取源码。 目录 一、摘要1.1 系统介绍1.2 项目录屏 二、研究内容2.1 课程类型管理模块2.2 课程管理模块2…...
Mysql分布式集群部署---MySQL集群Cluster将数据分成多个片段,每个片段存储在不同的服务器上
1.1 目的 部署MysqlCluster集群环境 1.2 MySQL集群Cluster原理 1 数据分片 MySQL集群Cluster将数据分成多个片段,每个片段存储在不同的服务器上。这样可以将数据负载分散到多个服务器上,提高系统的性能和可扩展性。 2. 数据同步 MySQL集群Cluster使…...

身份认证技术
身份认证是对系统的用户进行有效性、真实性验证。 1.口令认证方式 使用口令认证方式,用户必须具有一个唯一的系统标识,并且保证口令在系统的使用和存储过程中是安全的,同时口令在传输过程中不能被窃取、替换。另外特别要注意的是在…...
Centos7、Mysql8.0 load_file函数返回为空的终极解决方法--暨selinux的深入理解
零、问题背景 最近想换房,为了方便自己对比感兴趣的房子,因此决定将目标房源的基本信息放在表里,特别是要一目了然的看到众多房子的各种图纸和照片,因此决定要在Mysql8.0.34数据库中以二进制形式保存图片(抛开合理性和…...

基于Spring Boot的水产养殖管理系统
文章目录 项目介绍主要功能截图:部分代码展示设计总结项目获取方式🍅 作者主页:超级无敌暴龙战士塔塔开 🍅 简介:Java领域优质创作者🏆、 简历模板、学习资料、面试题库【关注我,都给你】 🍅文末获取源码联系🍅 项目介绍 基于Spring Boot的水产养殖管理系统,jav…...
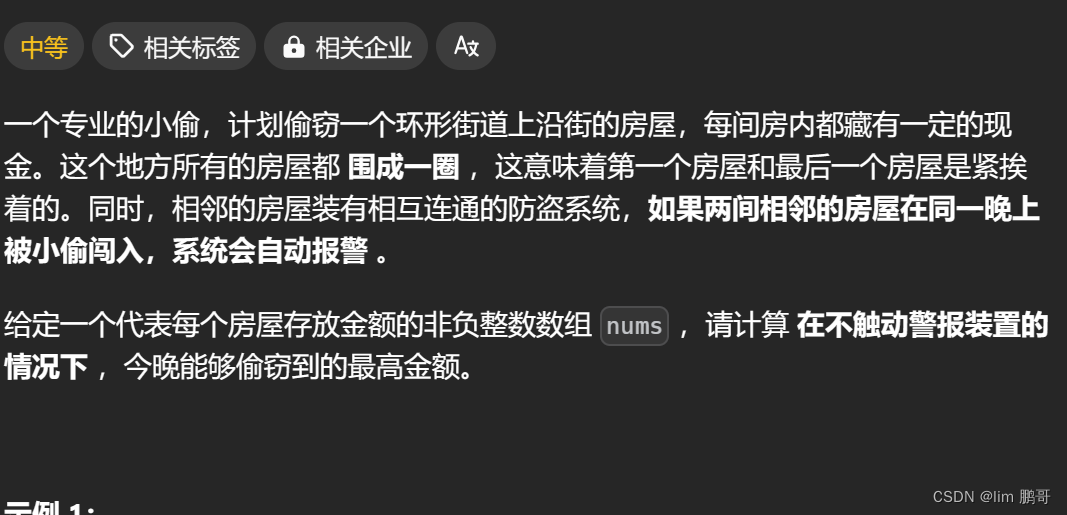
LCR 090. 打家劫舍 II(leetcode)动态规划
文章目录 前言一、题目分析二、算法原理1.状态表示2.状态转移方程3.初始化4.填表顺序5.返回值是什么 三、代码实现总结 前言 在本文章中,我们将要详细介绍一下LeetcodeLCR 090. 打家劫舍 II。采用动态规划解决,这是一道经典的多状态dp问题 一、题目分析…...
【小沐学Python】Python实现语音识别(Whisper)
文章目录 1、简介1.1 whisper简介1.2 whisper模型 2、安装2.1 whisper2.2 pytorch2.3 ffmpeg 3、测试3.1 命令测试3.2 代码测试:识别声音文件3.3 代码测试:实时录音识别 结语 1、简介 https://github.com/openai/whisper 1.1 whisper简介 Whisper 是…...
Nginx负载均衡实战
🎵负载均衡组件 ngx_http_upstream_module https://nginx.org/en/docs/http/ngx_http_upstream_module.html upstream模块允许Nginx定义一组或多组节点服务器组,使用时可以通过多种方式去定义服务器组 样例: upstream backend {server back…...
)
Redis skiplist源码解析(支持范围查询)
跳表是一个多层的有序链表,在跳表中进行查询操作时,查询代码可以从最高层开始查询。层数越高,结点数越少,同时高层结点的跨度会比较大。因此,在高层查询结点时,查询一个结点可能就已经查到了链表的中间位置…...
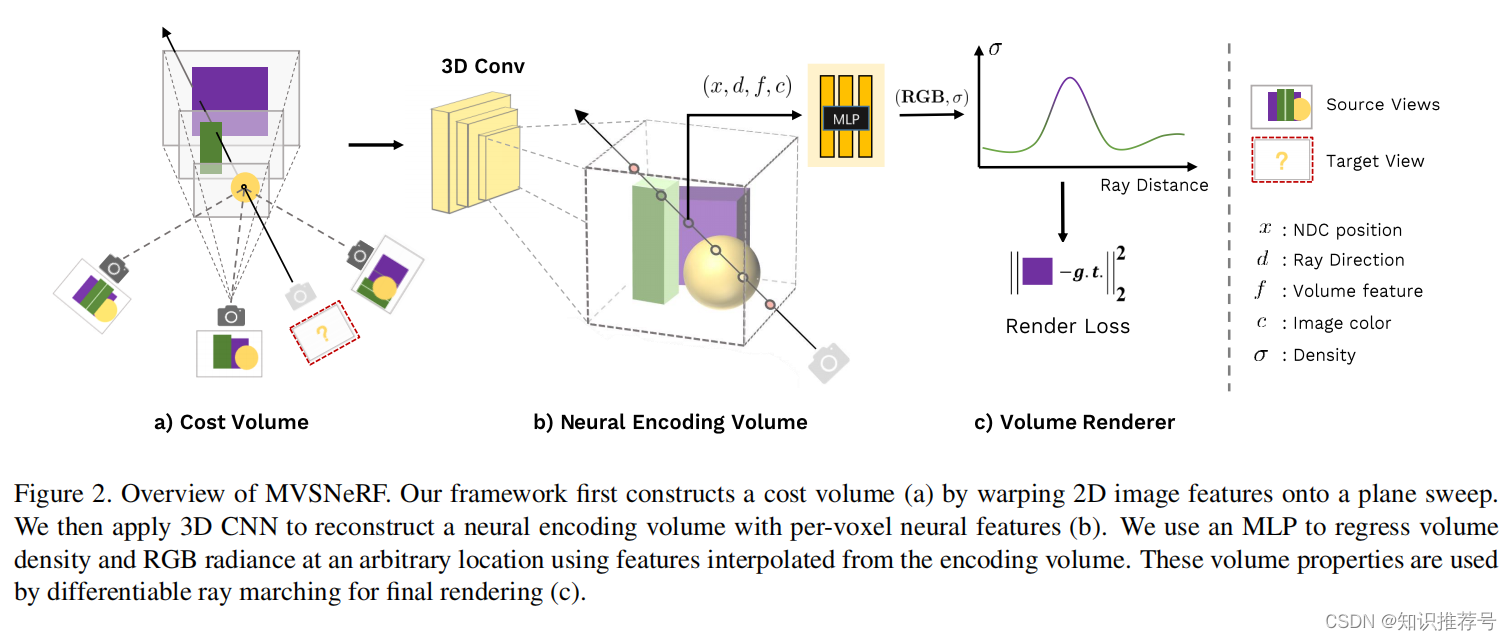
MVSNeRF:多视图立体视觉的快速推广辐射场重建(2021年)
MVSNeRF:多视图立体视觉的快速推广辐射场重建(2021年) 摘要1 引言2 相关工作3 MVSNeRF实现方法3.1 构建代价体3.2 辐射场的重建3.3 体渲染和端到端训练 3.4 优化神经编码体 Anpei Chen and Zexiang Xu and Fuqiang Zhao et al. MVSNeRF: Fast…...
)
华为OD机试真题-CPU算力分配-2023年OD统一考试(C卷)
题目描述: 现有两组服务器A和B,每组有多个算力不同的CPU,其中A[i]是A组第i个CPU的运算能力,B[i]是B组第i个CPU的运算能力。一组服务器的总算力是各CPU的算力之和。为了让两组服务器的算力相等,允许从每组各选出一个CPU进行一次交换,求两组服务器中,用于交换的CPU的算力,…...
)
校验数据是否重叠(各种操作符>,<,>=,<=,or,and)
最近接到一个需求,其中部分功能涉及到数据的重叠校验,并且录入的数据需要包含各种操作符。如果只通过java代码来查询并进行循环判断的话,判断情况会很复杂,幸好有同事的帮忙提供了一个用sql查询重叠部分的方法,现在分享…...

大一C语言作业 12.8
1.C 对一维数组初始化时,如果全部元素都赋了初值,可以省略数组长度。 这里没有指定数组长度,编译器会根据初始化列表的元素个数来确定数组长度。 2.C 在C语言中,字符数组是不能用赋值运算符直接赋值的。 3.C 在二维数组a中&#x…...
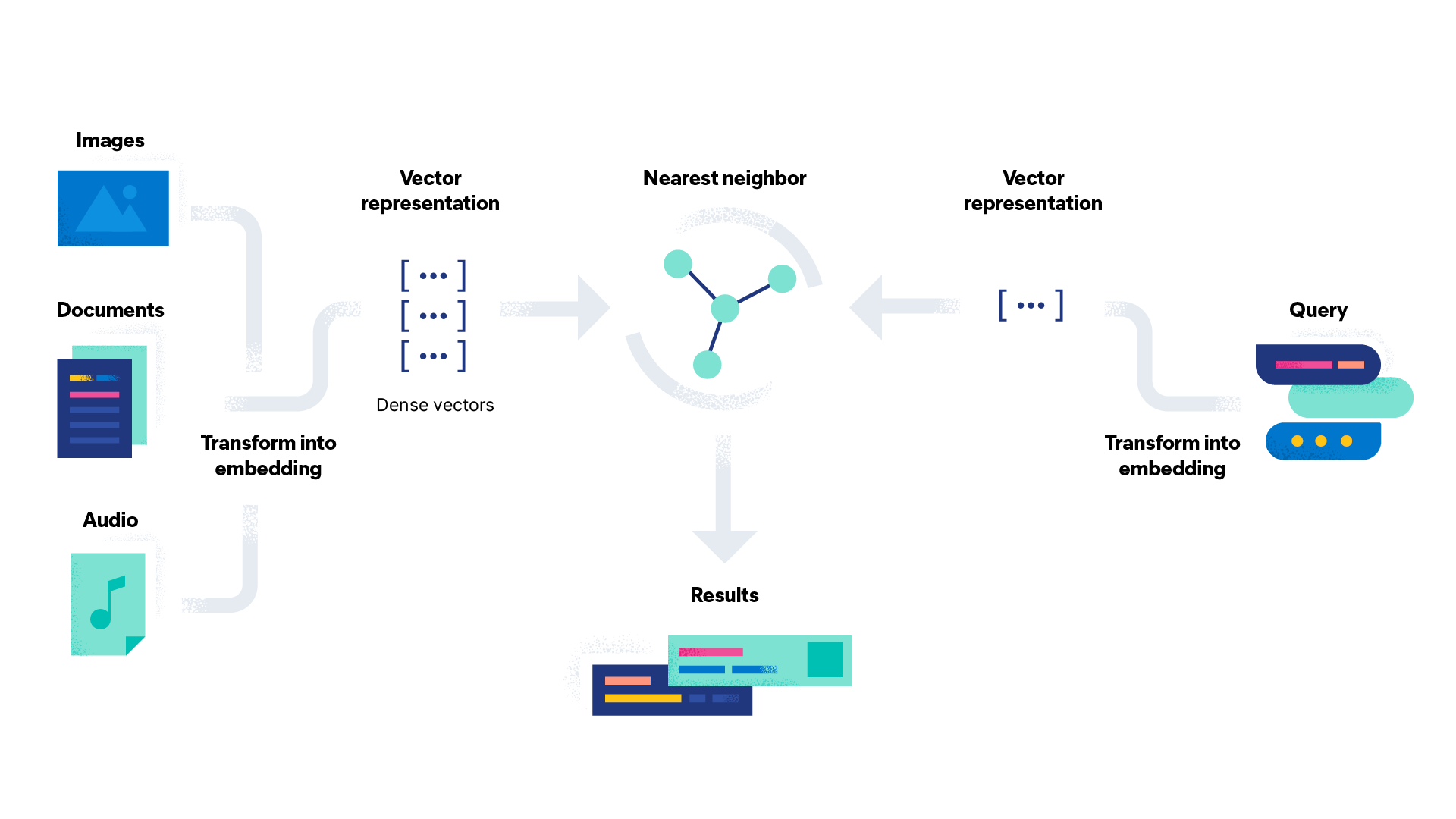
ELasticsearch:什么是语义搜索?
语义搜索定义 语义搜索是一种解释单词和短语含义的搜索引擎技术。 语义搜索的结果将返回与查询含义匹配的内容,而不是与查询中的单词字面匹配的内容。 语义搜索是一组搜索引擎功能,其中包括根据搜索者的意图及其搜索上下文理解单词。 此类搜索旨在通过…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...
