CCF 202104-2:邻域均值--C++
#include<iostream>
#include<bits/stdc++.h>using namespace std;int A[601][601];
int n;//长宽都为n个像素double FindNeighborSum(int i,int j,int r,int A[][601])
{int sum=0;//像素和 int gs=0;//领域 中的像素个数 for(int x=i-r;x<=i+r;x++)//找到每一个领域像素点 {for(int y=j-r;y<=j+r;y++){if(x>=0&&x<n){if(y>=0&&y<n){sum+=A[x][y];gs++;}}}}double result=(double)sum/gs;//要用double不能用int,不然等于t的数量会变多 return result;//
}int main()
{int L;//像素的取值范围int r;//领域的范围int t;//阈值,当领域内的均值小于或等于阈值t时是较暗区域cin>>n>>L>>r>>t;for(int i=0;i<n;i++){for(int j=0;j<n;j++)cin>>A[i][j];}int sum=0;//记录较暗区域个数 for(int i=0;i<n;i++){for(int j=0;j<n;j++)//对每一个像素点分析 {if(FindNeighborSum(i,j,r,A)<=t) sum++;}}cout<<sum;return 0;
}暴力求解:70分,要返回一个double类型的值,不然的话有些不是较暗区域的点也会被计为较暗区域
原本我想 分区域来运算,当邻域像素点个数为最大值(2*r+1)*(2*r+1)时用二维差分,否则用暴力
但是还是会超时
#include<iostream>
#include<bits/stdc++.h>using namespace std;int A[601][601];
int n;//长宽都为n个像素int d[601][601];//记录(i,j)点的前缀和 double FindNeighborSum(int i,int j,int r,int A[][601])
{int suml=0;//像素和 int gs=0;//领域 中的像素个数 for(int x=i-r;x<=i+r;x++)//找到每一个领域像素点 {for(int y=j-r;y<=j+r;y++){if(x>=0&&x<n){if(y>=0&&y<n){suml+=A[x][y];gs++;}}}}double result=(double)suml/gs;//要用double不能用int,不然等于t的数量会变多 return result;//
}int main()
{int L;//像素的取值范围int r;//领域的范围int t;//阈值,当领域内的均值小于或等于阈值t时是较暗区域memset(d,0,sizeof d);//将d清零 cin>>n>>L>>r>>t;for(int i=0;i<n;i++){for(int j=0;j<n;j++){cin>>A[i][j];d[i][j]=d[i][j-1]+d[i-1][j]-d[i-1][j-1]+A[i][j]; //cout<<d[i][j]<<endl;}}int sum=0;//记录较暗区域个数 int NeighborSum=0;//记录邻域中像素数值之和 double NeighborAvg=0;for(int i=0;i<n;i++){for(int j=0;j<n;j++)//对每一个像素点分析 { if(i-r>=0&&i+r<n&&j-r>=0&&j+r<n)//分区域来运算,当邻域像素点个数为最大值(2*r+1)*(2*r+1)时用差分,否则用暴力{NeighborSum=d[i+r][j+r]-d[i+r][j-r-1]-d[i-r-1][j+r]+d[i-r-1][j-r-1];NeighborAvg=(double)NeighborSum/((2*r+1)*(2*r+1));if(NeighborAvg<=t) sum++;}else{//邻域的上下左右有些地方不全 if(FindNeighborSum(i,j,r,A)<=t) sum++; } }}cout<<sum;return 0;
}从上面的分区域到下面的满分优化,关键是怎么得到邻域的像素点个数,上面的分区域方法如果所判断的像素点(i,j)的邻域没有缺少,即邻域像素点个数达到最大(2*r-1)*(2*r-1),如果(i,j)的邻域不完整,那就暴力的一个一个判断使得gs++来得到邻域中像素点的个数。
可以通过邻域的上下左右来求得邻域中像素点的个数
如图,如果此时红色笔圈起来的数7是当前判断到的像素,设为(i,j),r=2, 那么(i,j)的邻域就应该是如图画的正方形,红色直线=left=j-r; 橙色直线=right=j+r ,蓝色直线=top=i-r;绿色直线=buttom=i+r;
所以这个邻域中像素点的个数 等于 (right-left+1)*(buttom-top+1)
这是理想的情况,即邻域是完整的
当邻域不完整时,应该通过判断来调整上下左右的取值,但是像素点个数求法还是一样的
if(i-r<0)//上边不够
top=0;
else//上边够那么可能下边不够
{
if(i+r>=n)//下边不够
buttom=n-1;
}
if(j-r<0)//左边不够
left=0;
else
if(j+r>=n)//右边不够
right=n-1;
再用前缀和来求解一个区域中像素点的数值和

优化:用二维差分,记录一下我的第一次自己优化
#include<iostream>
#include<bits/stdc++.h>using namespace std;int A[601][601];
int n;//长宽都为n个像素int d[601][601];//记录(i,j)点的前缀和 int main()
{int L;//像素的取值范围int r;//领域的范围int t;//阈值,当领域内的均值小于或等于阈值t时是较暗区域memset(d,0,sizeof d);//将d清零 cin>>n>>L>>r>>t;for(int i=0;i<n;i++){for(int j=0;j<n;j++){cin>>A[i][j];d[i][j]=d[i][j-1]+d[i-1][j]-d[i-1][j-1]+A[i][j]; //cout<<d[i][j]<<endl;}}int sum=0;//记录较暗区域个数 int NeighborSum=0;//记录邻域中像素数值之和 double NeighborAvg=0;int Neighbor=0;//记录邻域中像素个数 int left=0,right=0,top=0,buttom=0;//记录邻域的上下左右,方便计数 for(int i=0;i<n;i++){for(int j=0;j<n;j++)//对每一个像素点分析 {//首先将邻域当作理想情况,后面通过判断再调整top=i-r;buttom=i+r;left=j-r;right=j+r;if(i-r<0)//上边不够top=0;else//上边够那么可能下边不够 {if(i+r>=n)//下边不够 buttom=n-1; }if(j-r<0)//左边不够left=0;else if(j+r>=n)//右边不够right=n-1; Neighbor=(buttom-top+1)*(right-left+1); //邻域中像素点个数 NeighborSum=d[buttom][right]-d[buttom][left-1]-d[top-1][right]+d[top-1][left-1];//cout<<NeighborSum<<endl;NeighborAvg=(double)NeighborSum/Neighbor;if(NeighborAvg<=t) sum++;} }cout<<sum;return 0;
}我自己的理解,之前看过一篇特别好的差分法的文章,可惜找不到了
差分法就是在输入的时候求得对应位置的前缀和,当你需要对某个区间或区域进行加减时不用一个一个加减,直接对前缀和数组操作
一维差分:
int n=10;
for(int i=0;i<n;i++)
{
cin>>A[i];
d[i]=d[i-1]+A[i];//前缀和数组,代表第i位以及前面所有数据的和
}//对[1,5]的数据全部加1
d[1]+=1;
d[5]-=1;//只需要对区间两端的前缀和数组进行操作即可
//A[i]=d[i]-d[i-1];//得到新的加一之和的值例题:非零段划分202109-2 非零段划分--C++-CSDN博客
二维差分:
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
cin>>A[i][j];
d[i][j]=d[i][j-1]+d[i-1][j]-d[i-1][j-1]+A[i][j];
}
}当i=3,j=3时,d[i][j]就是如图左上角的所有数之和

这样我们通过输入就可以得到每一个数的二维前缀和,当我们想要求一个区域的所有数之和(在本题中相对于求邻域中的所有数值之和),当我们想要求红色区域的所有数之和,可以用黄色区域所有数之和即d[4][5],减去蓝色区域所有数之和即d[4][2],再减去粉色区域所有数之和即d[1][5],重复减去的区域要加回来,加上d[2][2],就可以得到想要求的区域的所有数之和

差分法~超详细(公式+原理+例题)-CSDN博客
相关文章:

CCF 202104-2:邻域均值--C++
#include<iostream> #include<bits/stdc.h>using namespace std;int A[601][601]; int n;//长宽都为n个像素double FindNeighborSum(int i,int j,int r,int A[][601]) {int sum0;//像素和 int gs0;//领域 中的像素个数 for(int xi-r;x<ir;x)//找到每一个领域像素…...
基于JAVA+SpringBoot+Vue的前后端分离的医院信息智能化HIS系统
✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景介绍: 随着科技的不断发展&a…...

Kotlin Flow 操作符
前言 Kotlin 拥有函数式编程的能力,使用Kotlin开发,可以简化开发代码,层次清晰,利于阅读。 然而Kotlin拥有操作符很多,其中就包括了flow。Kotlin Flow 如此受欢迎大部分归功于其丰富、简洁的操作符,巧妙使…...
HarmonyOS4.0从零开始的开发教程08构建列表页面
HarmonyOS(六)构建列表页面 List组件和Grid组件的使用 简介 在我们常用的手机应用中,经常会见到一些数据列表,如设置页面、通讯录、商品列表等。下图中两个页面都包含列表,“首页”页面中包含两个网格布局ÿ…...

分布式环境下的session 共享-基于spring-session组件和Redis实现
1、问题概述 不是所有的项目都是单机模式的,当一个项目服务的局域比较广,用户体量比较大,数据量较大的时候,我们都会将项目部署到多台服务器上,这些个服务器都是分布在不同的区域,这样实现了项目的负载和并…...
docker基本管理和相关概念
docker是什么? docker是开源的应用容器引擎。基于go语言开发的。运行在Linux系统当中开源轻量级的“虚拟机”。 docker的容器技术可以在一台主机上轻松的为任何应用创建一个轻量级的,可移植的,自给自足的容器。 docker的宿主机是Linux系统…...
Linix服务器添加dns解析
Linix开通互联网域名地址出现,如下错误: 需要访问的服务器上添加dns解析 vim /etc/sysconfig/network-scripts/ifcfg-ens192 添加如下配置: DNS1202.96.134.13 重启网卡: systemctl restart network 注意如果是docker服务部署…...
llama.cpp部署(windows)
一、下载源码和模型 下载源码和模型 # 下载源码 git clone https://github.com/ggerganov/llama.cpp.git# 下载llama-7b模型 git clone https://www.modelscope.cn/skyline2006/llama-7b.git查看cmake版本: D:\pyworkspace\llama_cpp\llama.cpp\build>cmake --…...

STM32CubeMX+micro_ros_stm32cubemx_utils库
GitHub - micro-ROS/micro_ros_stm32cubemx_utils at humble 这个就是下载这个代码库以后的文件结构。其中sample_project.ioc就是平时STM32CubeMX的工程文件。类似于visual studio里面的项目文件 。打开以后是这个样子的: 可以看到跟本文后面的那些配置是几乎一模一…...

C语言有哪些预处理操作?
C语言的预处理是在编译之前对源代码进行处理的阶段,它主要由预处理器完成。预处理器是一个独立的程序,它负责对源代码进行一些文本替换和处理,生成经过预处理的代码。以下是C语言预处理的一些重要特性: 1,头文件包含 #…...

数据结构算法-希尔排序算法
引言 在一个普通的下午,小明和小森决定一起玩“谁是老板”的扑克牌游戏。这次他们玩的可不仅仅是娱乐,更是要用扑克牌来决定谁是真正的“大老板”。 然而,小明的牌就像刚从乱麻中取出来的那样,毫无头绪。小森的牌也像是被小丑掷…...

php使用vue.js实现省市区三级联动
参考gpt 有问题问gpt 实现效果 现省市区三级联动的方法可以使用PHP结合AJAX异步请求来实现。下面是一个简单的示例代码: HTML部分: <!DOCTYPE html> <html> <head><meta charset"UTF-8"><title>省市区三级联动…...

软件测试:测试用例八大要素模板
一、通用测试用例八要素 1、用例编号; 2、测试项目; 3、测试标题; 4、重要级别; 5、预置条件; 6、测试输入; 7、操作步骤; 8、预期输出 二、具体分析通用测试用例八要素 1、用例编号 一般是数字…...
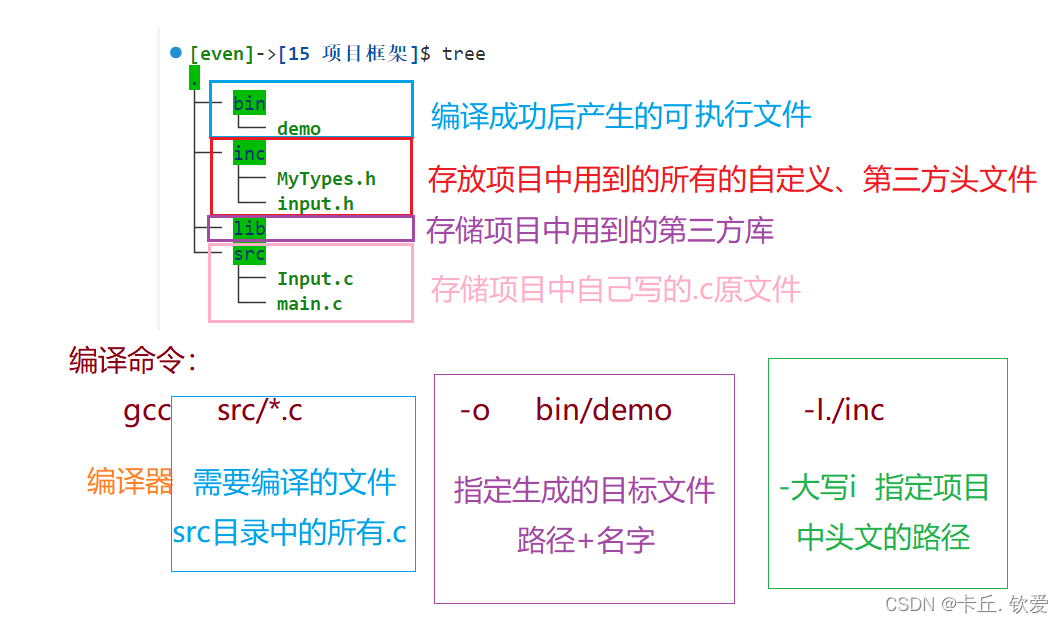
C语言进阶之路之顶峰相见篇
目录 一、学习目标 二、宏定义 预处理 宏的概念 带参宏 无值宏定义 三、条件编译 条件编译 条件编译的使用场景 四、头文件 头文件的作用 头文件的内容 头文件的基础语句: GCC编译器的4个编译步骤: 总结 一、学习目标 掌握宏定义含义和用…...
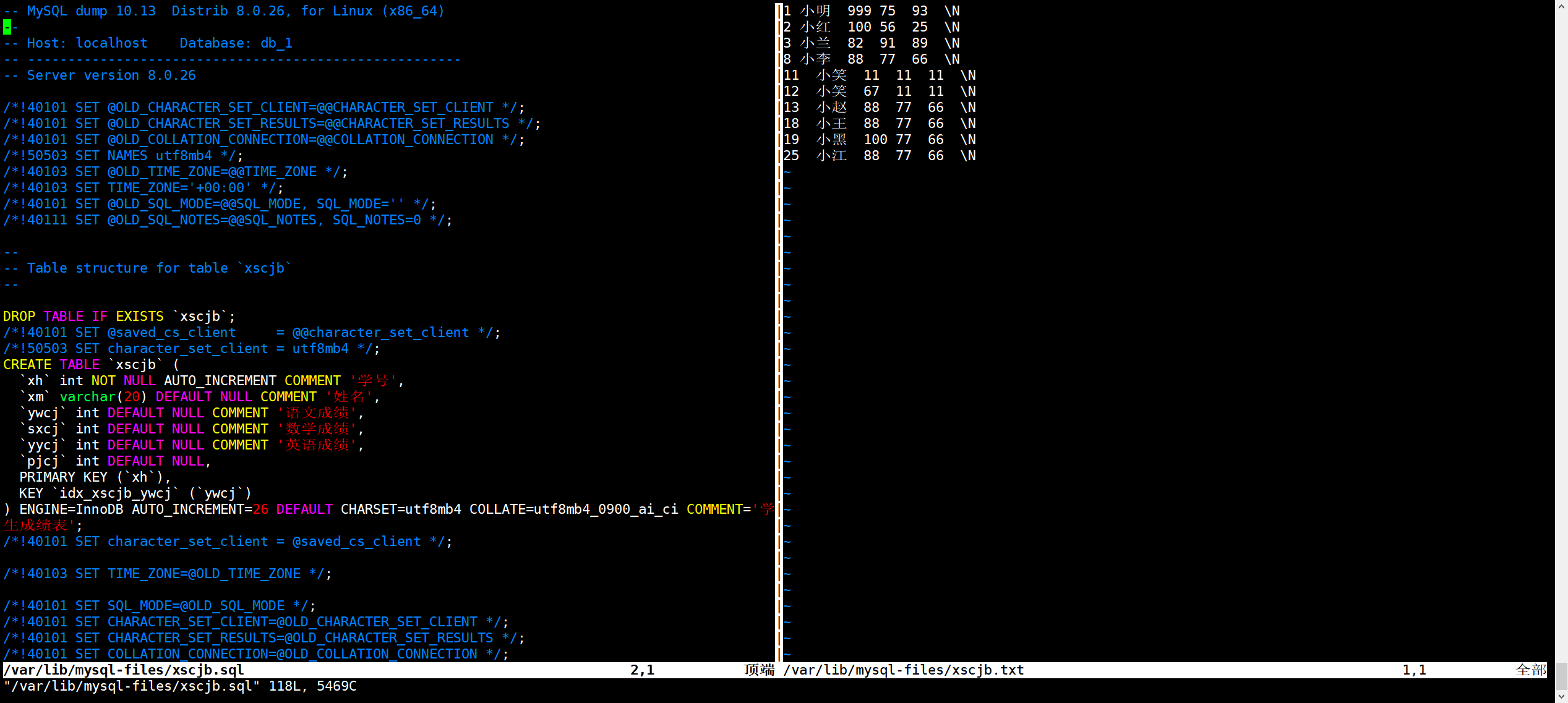
第76讲:MySQL数据库中常用的命令行工具的基本使用
文章目录 1.mysql客户端命令工具2.mysqladmin管理数据库的客户端工具3.mysqlbinlog查看数据库中的二进制日志4.mysqlshow统计数据库中的信息5.mysqldump数据库备份工具6.mysqllimport还原备份的数据7.source命令还原SQL类型的备份文件 MySQL数据库提供了很多的命令行工具&#…...

初级数据结构(二)——链表
文中代码源文件已上传:数据结构源码 <-上一篇 初级数据结构(一)——顺序表 | NULL 下一篇-> 1、链表特征 与顺序表数据连续存放不同,链表中每个数据是分开存放的,而且存放的位置尤其零散&#…...
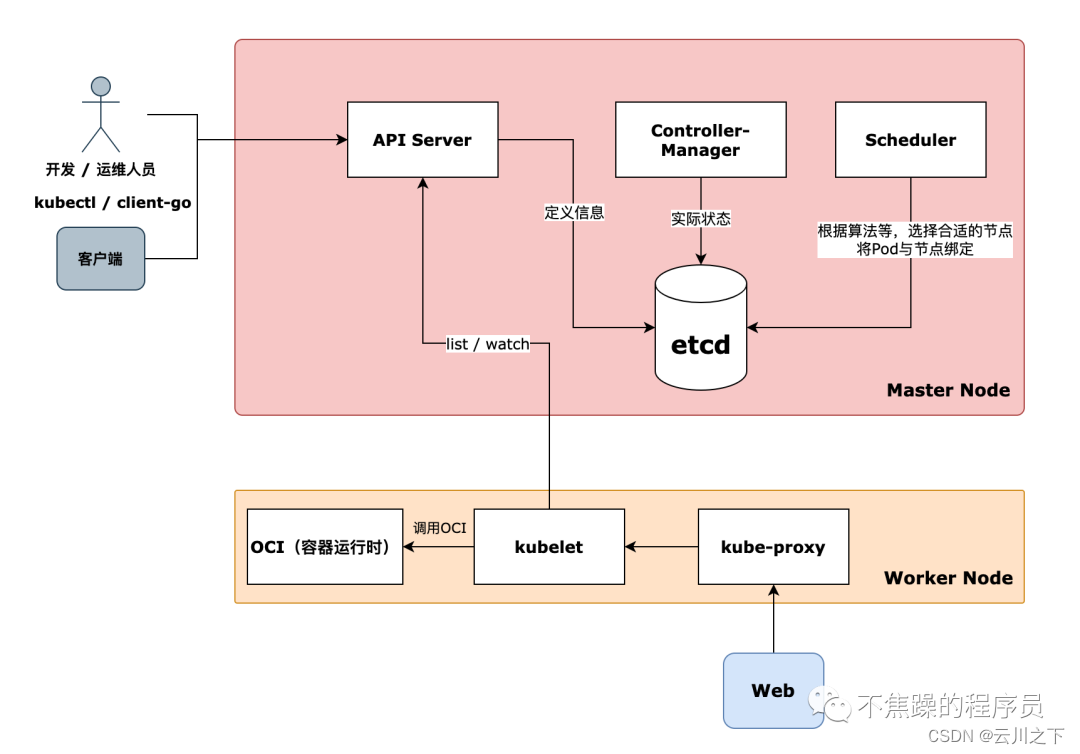
Kubernetes架构及核心部件
文章目录 1、Kubernetes集群概述1.1、概述1.2、通过声明式API即可 2、Kubernetes 集群架构2.1、Master 组件2.1.1、API Server2.1.2、集群状态存储2.1.3、控制器管理器2.1.4、调度器 2.2、Worker Node 组件2.2.1、kubelet2.2.2、容器运行时环境2.2.3、kube-proxy 2.3、图解架构…...

RAW和YUV的区别
RAW是指未经过任何压缩或处理的原始图像数据。在摄像头中,原始图像数据可以是来自图像传感器的未经处理的像素值。这些原始数据通常以一种Bayer模式的形式存在,其中每个像素仅包含一种颜色信息(红色、绿色或蓝色),需要…...
)
Linux常见问题-获取日志方法总结(Ubuntu/Debian)
1 日志基本路径和基础查看方法 在 Ubuntu 或 Debian 11 系统中,可以通过不同的日志文件来获取系统日志和内核日志。日志常见路径如下: /var/log/syslog:包含系统的整体日志,包括各种系统事件和服务日志。/var/log/auth.log&…...

【机器视觉技术栈】03 - 镜头
镜头 定焦镜头变焦镜头远心镜头 FA镜头与远心镜头的区别? 焦距越小畸变程度越大,精度要求不高的场景可以使用焦距大的FA镜头做尺寸测量,但焦距越大带来的问题就是整个机械设备越大。精度高的场景使用远心镜头进行尺寸测量。 光学基础知识…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

Java数组Arrays操作全攻略
Arrays类的概述 Java中的Arrays类位于java.util包中,提供了一系列静态方法用于操作数组(如排序、搜索、填充、比较等)。这些方法适用于基本类型数组和对象数组。 常用成员方法及代码示例 排序(sort) 对数组进行升序…...

MLP实战二:MLP 实现图像数字多分类
任务 实战(二):MLP 实现图像多分类 基于 mnist 数据集,建立 mlp 模型,实现 0-9 数字的十分类 task: 1、实现 mnist 数据载入,可视化图形数字; 2、完成数据预处理:图像数据维度转换与…...

基于Python的气象数据分析及可视化研究
目录 一.🦁前言二.🦁开源代码与组件使用情况说明三.🦁核心功能1. ✅算法设计2. ✅PyEcharts库3. ✅Flask框架4. ✅爬虫5. ✅部署项目 四.🦁演示效果1. 管理员模块1.1 用户管理 2. 用户模块2.1 登录系统2.2 查看实时数据2.3 查看天…...

大模型智能体核心技术:CoT与ReAct深度解析
**导读:**在当今AI技术快速发展的背景下,大模型的推理能力和可解释性成为业界关注的焦点。本文深入解析了两项核心技术:CoT(思维链)和ReAct(推理与行动),这两种方法正在重新定义大模…...
