Project Euler 865 Triplicate Numbers(线性dp)
题目

能通过每次消除3个一样的数字,最终把数字消成空的数字是合法的,
求串长度不超过n的,没有前导0的数字中,合法的数字的个数
n=10000,答案对998244353取模,只需要输出数字
思路来源
乱搞AC
题解
暴力先把n=9求出来,有了n=9和n=30,都对上之后就敢交n=1e4了
dp[i]表示长度为i的合法方案,显然i是3的倍数是才有合法方案
然后还要分有没有前导0,于是就多开了一维,虽然后来发现dp[i][0]没有用到
dp[i][0]表示没有前导0限制的方案数,dp[i][1]表示有前导0限制的方案数
考虑最后一个数是怎么填的,只有四种情况,
其中xxx的长度也需要满足3的倍数,
①xxx111
②1xxx11
③11xxx1
④1xxx1yyy1
此外,为了避免重复,
需要保证这三个1在这一段中是位置处于最后的,能被消掉的3个1
第一种情况显然满足,第二三四种情况,都需要保证,
中间的xxx、yyy不管怎么消,都不能有1漏在最左边或最右边
比如11001111,100011122211这些,下划线的3个1不是位于最后的3个1,就会计数重复
而101110011就是合法的,中间011100怎么消,都不会导致1出现在最左或最右,
只要和想消的3个1不相邻,就能构成一组唯一计数的方案
所以,定义f[i]用于辅助转移,
f[i]表示长度为i时,0-9随便填,能消完,
但是不管怎么消,中途1都不能出现在最左或最右的方案数
然后就分情况转移的四种情况讨论即可,
第一种情况转移是O(1)的,
第二三种情况1xxx11和11xxx1是可以合并成一种转移,给系数乘2的,转移是O(n)的,
第三种情况暴力转移是O(n^2)的,但可以一边求一边暴力维护卷积mul,这样转移就是O(n)的了
第二三种情况合并一下,那就是三种情况,
除去第一种情况O(1)转移外,都要考虑前导0的问题
每种情况填的数字分是否占据了第一个位置讨论一下,
填的是第一个位置时,只能填9个数字,否则能填10个数字
求了f、dp[i][0]、dp[i][1]三个数组,
所以,总的转移式子一共3*(1+2*2)个
答案是dp数组的前缀和
代码1(dp)
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
//#define int long long
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int N=1e4+10,M=10000,mod=998244353;
//dpi0:没前导0限制 dpi1:有前导0限制
//fi:两边只能填1-9,中间可以填0,两边不是0,且以任意顺序炸,0不会两边擦边的方案数
int t,f[N],dp[N][2],mul2[N],sum[N],ans;//ein,nit;
ll v;
int modpow(int x,int n,int mod){int res=1;for(;n;n>>=1,x=1ll*x*x%mod){if(n&1)res=1ll*res*x%mod;}return res;
}
void add(int &x,int y){x=(x+y)%mod;}
void sol(){//ein=8ll*modpow(9,mod-2,mod)%mod;//nit=9ll*modpow(10,mod-2,mod)%mod;dp[3][0]=10;dp[3][1]=9;sum[3]=f[3]=9;for(int i=6;i<=M;i+=3){add(f[i],9ll*f[i-3]%mod);//000-888add(dp[i][1],10ll*dp[i-3][1]%mod);//0-9add(dp[i][0],10ll*dp[i-3][0]%mod);//0-9//printf("i:%d dp:%d\n",i,dp[i]);for(int j=6;j<=i;j+=3){if(j==i){//只能填1-9//printf("j:%d dpj-3:%d\n",j,dp[j-3]);add(f[i],18ll*f[j-3]%mod);add(dp[i][1],18ll*f[j-3]%mod);//110001,100011 不能与相邻相同add(dp[i][0],20ll*f[j-3]%mod);//110001,100011 不能与相邻相同if(j>=9){add(f[i],9ll*mul2[j-3]%mod);add(dp[i][1],9ll*mul2[j-3]%mod);//100010001 不能与相邻相同add(dp[i][0],10ll*mul2[j-3]%mod);//100010001 不能与相邻相同}}else{//能填0-9add(f[i],18ll*f[j-3]%mod*f[i-j]%mod);add(dp[i][1],20ll*f[j-3]%mod*dp[i-j][1]%mod);//110001,100011 不能与相邻相同add(dp[i][0],20ll*f[j-3]%mod*dp[i-j][0]%mod);//110001,100011 不能与相邻相同if(j>=9){add(f[i],9ll*mul2[j-3]%mod*f[i-j]%mod);add(dp[i][1],10ll*mul2[j-3]%mod*dp[i-j][1]%mod);//100010001 不能与相邻相同add(dp[i][0],10ll*mul2[j-3]%mod*dp[i-j][0]%mod);//100010001 不能与相邻相同}}}for(int j=3;j<i;j+=3){//add(mul[i],1ll*ein*dp[j]%mod*ein%mod*dp[i-j]%mod);add(mul2[i],1ll*f[j]%mod*f[i-j]%mod);}//printf("i:%d dp0:%d dp1:%d mul:%d\n",i,dp[i][0],dp[i][1],mul2[i]);sum[i]=(sum[i-3]+dp[i][1])%mod;}
}
int main(){//sci(t);scanf("%lld",&v);v%=mod;printf("%d\n",(int)v);//cin>>t;sol();int m=M/3*3,ans=sum[m];printf("%d\n",ans);return 0;
}代码2(暴力打表)
打表知,T(6)=261,T(9)=9504
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
//#define int long long
typedef long long ll;
typedef double db;
typedef pair<ll,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define scll(a) scanf("%lld",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
const int N=1e4+10,M=9,mod=998244353;
int t,ans,stk[15],c,cnt;
int main(){sci(t);int l=1,r=1e9;rep(i,l,r-1){int c=0;for(int j=i;j;j/=10){int v=j%10;if(c>=2 && stk[c]==stk[c-1] && stk[c]==v)c-=2;else stk[++c]=v;}if(!c){//printf("i:%d\n",i);cnt++;//if(cnt==10)break;}}printf("%d\n",cnt);return 0;
}
//T(6)=261
//T(9)=9504相关文章:

Project Euler 865 Triplicate Numbers(线性dp)
题目 能通过每次消除3个一样的数字,最终把数字消成空的数字是合法的, 求串长度不超过n的,没有前导0的数字中,合法的数字的个数 n10000,答案对998244353取模,只需要输出数字 思路来源 乱搞AC 题解 暴力…...

计算机网络测试题第二部分
前言:如果没有做在线测试请自主独立完成,本篇文章只作为学习计算机网络的参考,题库中的题存在一定错误和不完整,请学习时,查找多方书籍论证,独立思考,如果存在疑虑可以评论区讨论。查看时,请分清…...
linux 15day apache apache服务安装 httpd服务器 安装虚拟主机系统 一个主机 多个域名如何绑定
目录 一、apache安装二、访问控制总结修改默认网站发布目录 三、虚拟主机 一、apache安装 [rootqfedu.com ~]# systemctl stop firewalld [rootqfedu.com ~]# systemctl disable firewalld [rootqfedu.com ~]# setenforce 0 [rootqfedu.com ~]# yum install -y httpd [rootqfe…...
Linux和Windows环境下如何使用gitee?
1. Linux 1.1 创建远程仓库 1.2 安装git sudo yum install -y git 1.3 克隆远程仓库到本地 git clone 地址 1.4 将文件添加到git的暂存区(git三板斧之add) git add 文件名 # 将指定文件添加到git的暂存区 git add . # 添加新文件和修改过的…...

Docker安装教程
docker官网 1.卸载旧版 yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotate \docker-engine2.配置Docker的yum库 安装yum工具 yum install -y yum-utils配置Docker的yum源 yum-config-ma…...

【PWN】学习笔记(二)【栈溢出基础】
课程教学 课程链接:https://www.bilibili.com/video/BV1854y1y7Ro/?vd_source7b06bd7a9dd90c45c5c9c44d12e7b4e6 课程附件: https://pan.baidu.com/s/1vRCd4bMkqnqqY1nT2uhSYw 提取码: 5rx6 C语言函数调用栈 一个栈帧保存的是一个函数的状态信息&…...

02-Nacos和Eureka的区别与联系
Nacos和Eureka的区别 联系 Nacos和Eureka整体结构类似: 都支持服务注册, 服务拉取, 采用心跳方式对服务提供者做健康监测的功能 区别 Nacos支持服务端主动检测服务提供者状态: 临时实例采用心跳模式,非临时实例采用主动检测模式但对服务器压力比较大(不推荐) 心跳模式: 服务…...

常见的Linux系统版本
在介绍常见的Linux系统版本之前,首先需要区分Linux系统内核与Linux发行套件系统的不同。Linux系统内核指的是一个由Linus Torvalds负责维护,提供硬件抽象层、硬盘及文件系统控制及多任务功能的系统核心程序。而Linux发行套件系统是我们常说的Linux操作系…...

基于JavaWeb+SSM+Vue微信小程序的科创微应用平台系统的设计和实现
基于JavaWebSSMVue微信小程序的科创微应用平台系统的设计和实现 源码获取入口Lun文目录前言主要技术系统设计功能截图订阅经典源码专栏Java项目精品实战案例《500套》 源码获取 源码获取入口 Lun文目录 1系统概述 1 1.1 研究背景 1 1.2研究目的 1 1.3系统设计思想 1 2相关技术…...
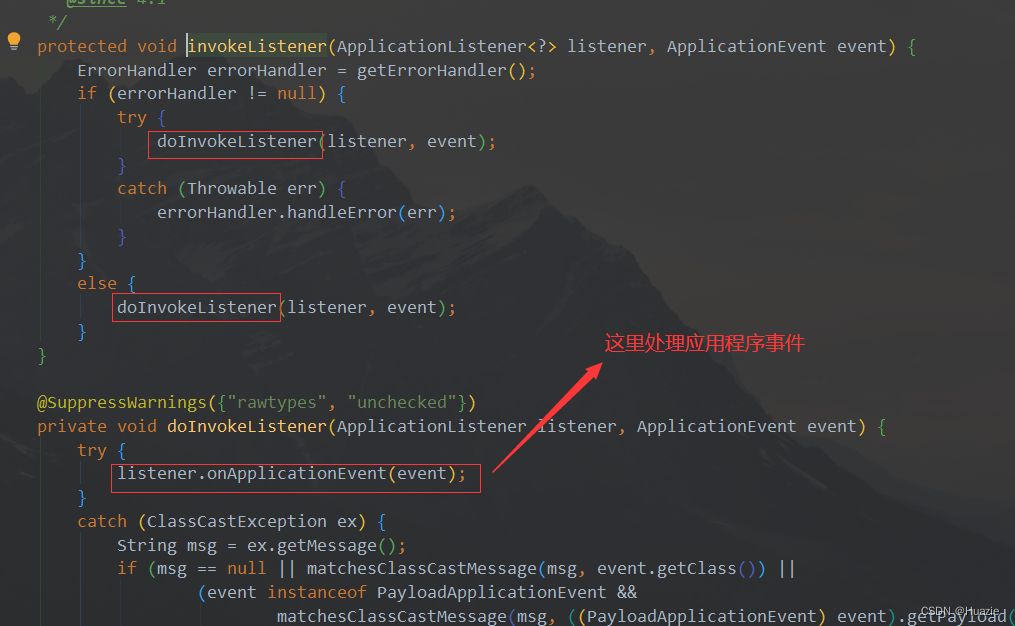
【Spring Boot 源码学习】ApplicationListener 详解
Spring Boot 源码学习系列 ApplicationListener 详解 引言往期内容主要内容1. 初识 ApplicationListener2. 加载 ApplicationListener3. 响应应用程序事件 总结 引言 书接前文《初识 SpringApplication》,我们从 Spring Boot 的启动类 SpringApplication 上入手&am…...

HCIP---RSTP/MSTP
文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 前言 STP协议虽然能够解决环路问题,但是收敛速度慢,影响了用户通信质量。IEEE于2001年发布的802.1w标准定义了快速生成树协议RSTP(Rapid Spanning-Tree Proto…...

探索开源游戏的乐趣与无限可能 | 开源专题 No.47
CleverRaven/Cataclysm-DDA Stars: 9.0k License: NOASSERTION Cataclysm:Dark Days Ahead 是一个回合制的生存游戏,设定在一个后启示录世界中。尽管有些人将其描述为 “僵尸游戏”,但 Cataclysm 远不止于此。在这个残酷、持久、程序生成的世…...

springboot_3.2_freemark_基础环境配置
springboot_3.2_freemark_基础环境配置 一、前言二、环境三、相关资料四、目标五、默认配置项六、构建springboot 3.2项目6.1 pom.xml 内容:6.2 启动类6.3 添加ftlh模板6.4 controller内容6.5 bootstrap.yml配置 七、总结 一、前言 FreeMarker 是一款模板引擎&…...

【MySQL】MySQL 在 Centos 7环境安装教程
文章目录 1.卸载不要的环境2.检查系统安装包3.获取mysql官方yum源4.安装mysql yum 源,对比前后yum源5.安装mysql服务6.查看配置文件和数据存储位置7.启动服务和查看启动服务8.登录9.配置my.cnf 1.卸载不要的环境 先检查是否有mariadb存在 ps ajx |grep mariadb如果…...

有病但合理的 ChatGPT 提示语
ChatGPT 面世一年多了,如何让大模型输出高质量内容,让提示词工程成了一门重要的学科。以下是一些有病但合理的提示词技巧,大部分经过论文证明,有效提高 ChatGPT 输出质量: 1️⃣ Take a deep breath. 深呼吸 ✨ 作用…...
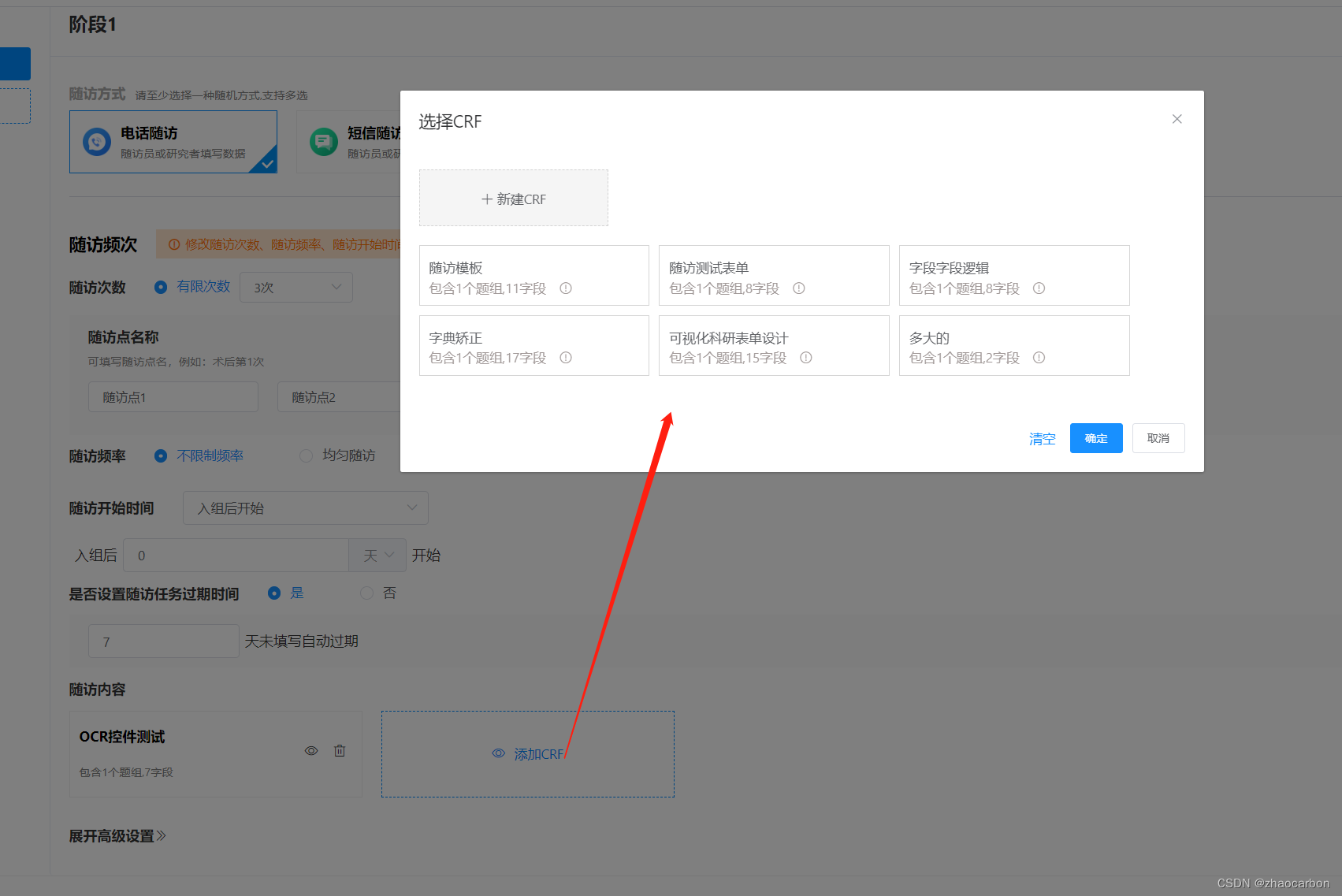
this.$emit(‘update:isVisible‘, false)作用
这个写是不是很新颖,传父组件传值!这是什么鬼。。。 假设你有以下逻辑业务。在A页面弹出一个组件B,A组件里面使用B组件,是否展示B组件你使用的是baselineShow变量控制! <BaselineData :isVisible.sync"basel…...

CnetSDK .NET OCR Library SDK Crack
CnetSDK .NET OCR Library SDK Crack CnetSDK .NET OCR Library SDK 是一款高精度 .NET OCR 扫描仪软件,用于从图像中识别字符,如文本、手写和符号。该.NET OCR库软件采用Tesseract OCR引擎技术,将字符识别准确率提高高达99%。通过将 .NET OC…...
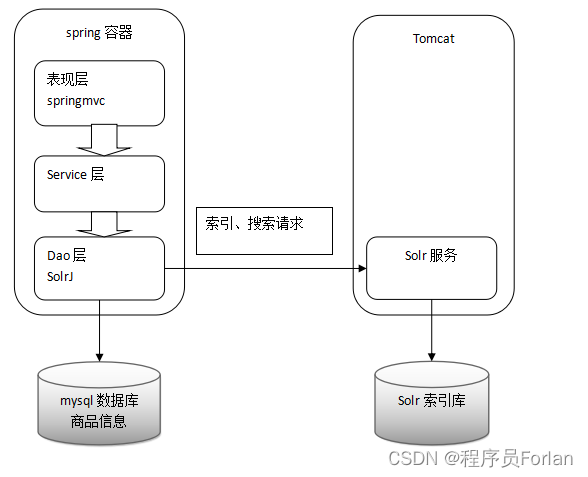
基于Solr的全文检索系统的实现与应用
文章目录 一、概念1、什么是Solr2、与Lucene的比较区别1)Lucene2)Solr 二、Solr的安装与配置1、Solr的下载2、Solr的文件夹结构3、运行环境4、Solr整合tomcat1)Solr Home与SolrCore2)整合步骤 5、Solr管理后台1)Dashbo…...
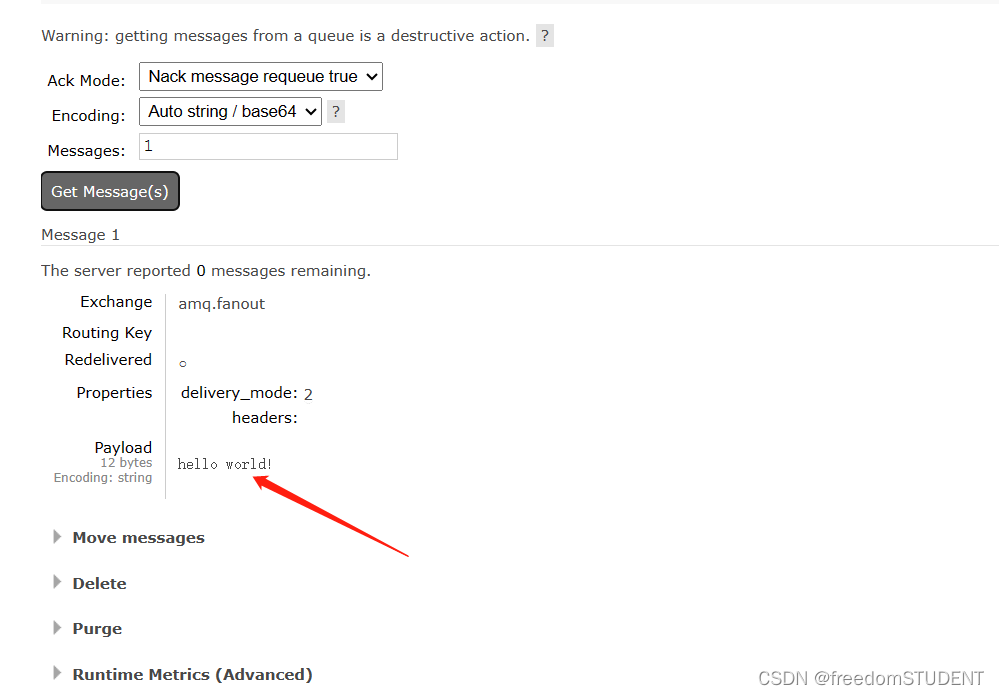
【rabbitMQ】rabbitMQ控制台模拟收发消息
目录 1.新建队列 2.交换机绑定队列 3.查看消息是否到达队列 总结: 1.新建队列 2.交换机绑定队列 点击amq.fonout 3.查看消息是否到达队列 总结: 生产者(publisher)发送消息,先到达交换机,再到队列&…...

Java NIO, IO 整理
NIO: IO多路复用: 参考: Redis(六)单线程I/O多路复用模型浅析_单线程多路复用-CSDN博客 Java NIO 详解_java nio详解_开发菜鸡的博客-CSDN博客 Java Socket 之 NIO - 掘金 答应我,这次搞懂 I/O 多路复用!_小林coding的博客-CS…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
