IDEA启动失败报错解决思路
IDEA启动失败报错解决思路
背景:在IDEA里安装插件失败,重启后直接进不去了,然后分析问题解决问题的过程记录下来。方便下次遇到快速解决。也是一种解决问题的思路,分享出去。
启动报错信息

Internal error. Please refer to https://jb.gg/ide/critical-startup-errorscom.intellij.diagnostic.PluginException: Key com.itangcent.idea.plugin.settings.xml.ApplicationSettingsComponent duplicated; existingAdapter: ServiceAdapter(descriptor=ServiceDescriptor(interface='null', serviceImplementation='com.itangcent.idea.plugin.settings.xml.ApplicationSettingsComponent', testServiceImplementation='null', headlessImplementation='null', overrides=false, configurationSchemaKey='null', preload=FALSE, client=null), pluginDescriptor=PluginDescriptor(name=EasyYapi, id=com.itangcent.idea.plugin.easy-yapi, descriptorPath=easy-yapi-java.xml, path=d:\user\wfq100426\Application Data\JetBrains\IdeaIC2023.2\plugins\easy-yapi, version=2.6.8.212.0, package=null, isBundled=false)); descriptor=com.itangcent.idea.plugin.settings.xml.ApplicationSettingsComponent, app=Application (containerState PRE_INIT) , current plugin=com.itangcent.idea.plugin.easy-apiat com.intellij.serviceContainer.ComponentManagerImpl.registerServices(ComponentManagerImpl.kt:566)at com.intellij.serviceContainer.ComponentManagerImpl.registerComponents(ComponentManagerImpl.kt:257)at com.intellij.openapi.client.ClientAwareComponentManager.registerComponents(ClientAwareComponentManager.kt:48)at com.intellij.ide.bootstrap.AppPreInitKt$initServiceContainer$2.invokeSuspend(appPreInit.kt:41)at com.intellij.ide.bootstrap.AppPreInitKt$initServiceContainer$2.invoke(appPreInit.kt)at com.intellij.ide.bootstrap.AppPreInitKt$initServiceContainer$2.invoke(appPreInit.kt)at kotlinx.coroutines.intrinsics.UndispatchedKt.startUndispatchedOrReturn(Undispatched.kt:78)at kotlinx.coroutines.BuildersKt__Builders_commonKt.withContext(Builders.common.kt:167)at kotlinx.coroutines.BuildersKt.withContext(Unknown Source)at com.intellij.diagnostic.TracerKt.subtask(tracer.kt:45)at com.intellij.diagnostic.TracerKt.subtask$default(tracer.kt:34)at com.intellij.ide.bootstrap.AppPreInitKt.initServiceContainer(appPreInit.kt:40)at com.intellij.ide.bootstrap.AppPreInitKt$initServiceContainer$1.invokeSuspend(appPreInit.kt)at kotlin.coroutines.jvm.internal.BaseContinuationImpl.resumeWith(ContinuationImpl.kt:33)at kotlinx.coroutines.UndispatchedCoroutine.afterResume(CoroutineContext.kt:270)at kotlinx.coroutines.AbstractCoroutine.resumeWith(AbstractCoroutine.kt:102)at kotlin.coroutines.jvm.internal.BaseContinuationImpl.resumeWith(ContinuationImpl.kt:46)at kotlinx.coroutines.DispatchedTask.run(DispatchedTask.kt:106)at kotlinx.coroutines.scheduling.CoroutineScheduler.runSafely(CoroutineScheduler.kt:584)at kotlinx.coroutines.scheduling.CoroutineScheduler$Worker.executeTask(CoroutineScheduler.kt:793)at kotlinx.coroutines.scheduling.CoroutineScheduler$Worker.runWorker(CoroutineScheduler.kt:697)at kotlinx.coroutines.scheduling.CoroutineScheduler$Worker.run(CoroutineScheduler.kt:684)-----
Your JRE: 17.0.8+7-b1000.22 amd64 (JetBrains s.r.o.)
C:\Program Files\JetBrains\IntelliJ IDEA Community Edition 2023.2.2\jbr
阅读报错信息并解决问题
报错类型:Internal error 内部错误
日志中说请看这个地址:https://jb.gg/ide/critical-startup-errors
com.intellij.diagnostic.PluginException: Key com.itangcent.idea.plugin.settings.xml.ApplicationSettingsComponent duplicated; existingAdapter:
插件异常,应用配置组件重复
那原因就是插件搞的报错导致启动失败
current plugin=com.itangcent.idea.plugin.easy-api
那就是easy-api这个插件搞的
再去看日志里提到的这个网址

这个网址讲述了这个启动错误可能的一些原因以及一些解决办法
我们这种插件异常符合第二种解决方案,直接去插件目录里删除这个问题插件
2. Delete the third-party plug-ins directory (idea.plugins.path in the user's home directory, depends on the OS and IDE version. Please be aware that default locations have changed in 2020.1 release). You can bisect the plug-ins to find the offending one and remove only that plug-in, keeping the working plug-ins.
这个第二点的 third-party plug-ins directory 这个文字是个超链接,点开地址 https://intellij-support.jetbrains.com/hc/en-us/articles/206544519
这里可以看到他们标明了各平台IDEA的一些文件存储的位置

我目前用的windows,plugins目录就是
%APPDATA%\JetBrains\IntelliJIdea2022.2\plugins
%APPDATA%是个APP数据目录的系统变量,在windows打开cmd输出看下我电脑实际路径是多少

复制这个路径拼接好插件路径进入这个目录

好的很啊,事情变得有趣了,手动进去APPDATA目录看看去


可以看到我已经手动找到了他们的Plugins目录,原因很简单,新版本的目录变了,文档的是根据IntelliJIdea2022.2版本的情况写的,所以这个地方灵活应变一下就可以解决了
我把这个easy-api(报错的)和easy-yapi(安装这个插件过程后重启IDEA启动报错)两个涉事嫌疑犯目录剪切出来放到最外面去(不要删除,防止又要放回去~)

再启动idea,成功!

我再重新安装easy-yapi去就可以了
安装成功

相关文章:

IDEA启动失败报错解决思路
IDEA启动失败报错解决思路 背景:在IDEA里安装插件失败,重启后直接进不去了,然后分析问题解决问题的过程记录下来。方便下次遇到快速解决。也是一种解决问题的思路,分享出去。 启动报错信息 Internal error. Please refer to https…...
密码学学习笔记(二十三):哈希函数的安全性质:抗碰撞性,抗第一原象性和抗第二原象性
在密码学中,哈希函数是一种将任意长度的数据映射到固定长度输出的函数,这个输出通常称为哈希值。理想的哈希函数需要具备几个重要的安全性质,以确保数据的完整性和验证数据的来源。这些性质包括抗碰撞性、抗第一原象性和抗第二原象性。 抗碰…...

STM32-GPIO编程
一、GPIO 1.1 基本概念 GPIO(General-purpose input/output)通用输入输出接口 --GP 通用 --I input输入 --o output输出 通用输入输出接口GPIO是嵌入式系统、单片机开发过程中最常用的接口,用户可以通过编程灵活的对接口进行控制,…...
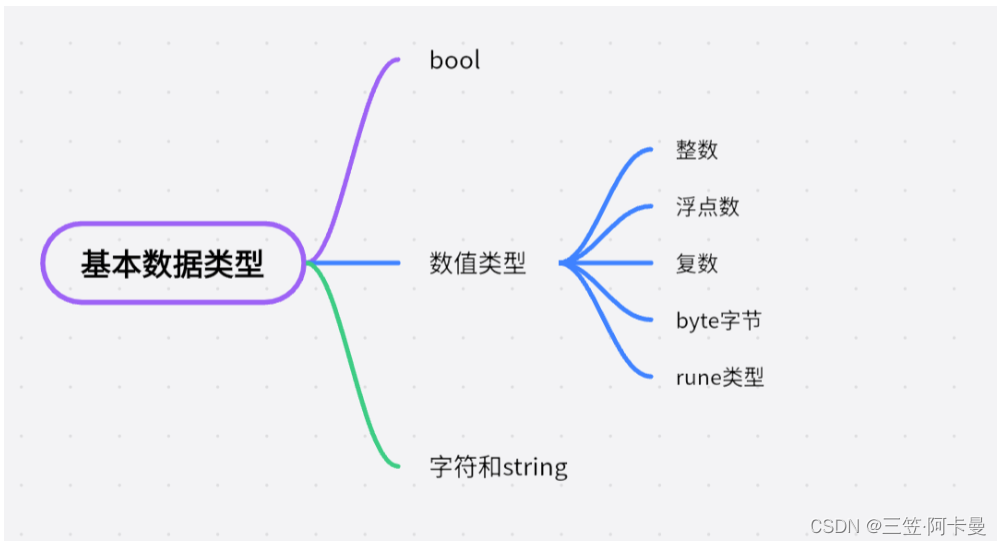
Go语言基础知识学习(一)
Go基本数据类型 bool bool型值可以为true或者false,例子: var b bool true数值型 类型表示范围int8有符号8位整型-128 ~ 127int16有符号16位整型-32768 ~ 32767int32有符号32位整型-2147783648 ~ 2147483647int64有符号64位整型uint8无符号8位整型0 ~ 255uint16…...

Vue 3项目的目录结构
使用vite创建完VUE项目后,使用VS Code编辑器打开项目目录,可以看到一个默认生成的项目目录结构 下图是目录结构: 详细介绍.vscode:存放VS Code编辑器的相关配置。 node_modules:存放项目的各种依赖和安装的插件。…...
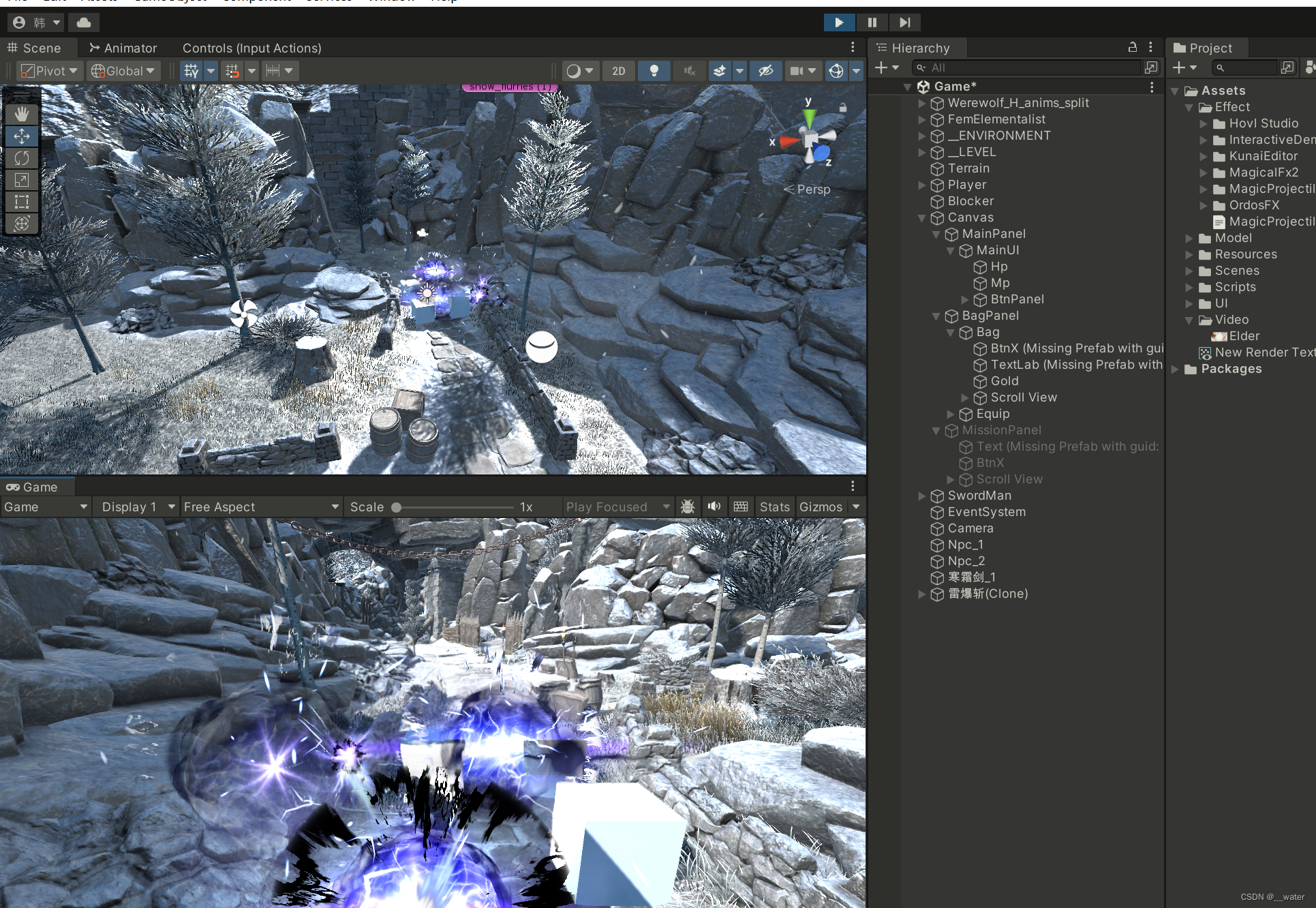
RPG项目01_技能释放
基于“RPG项目01_新输入输出”, 修改脚本文件夹中的SkillBase脚本: using System; using System.Collections; using System.Collections.Generic; using UnityEngine; using UnityEngine.Events; //回复技能,魔法技能,物理技能…...

Leetcode—209.长度最小的子数组【中等】
2023每日刷题(五十六) Leetcode—209.长度最小的子数组 实现代码 class Solution { public:int minSubArrayLen(int target, vector<int>& nums) {int left 0, right 0;int ans nums.size() 1, s 0;for(; right < nums.size(); righ…...
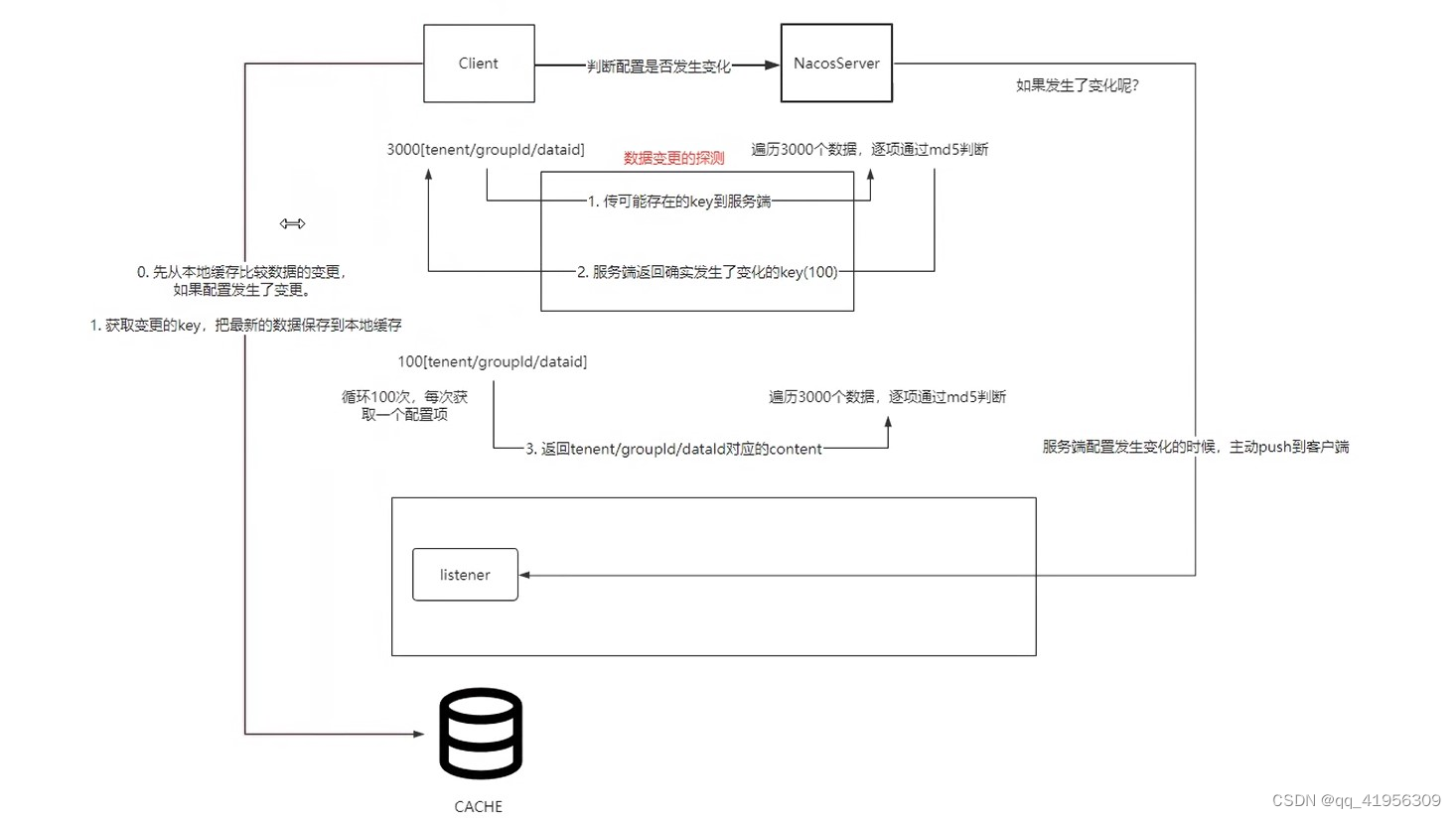
Nacos源码解读12——Nacos中长连接的实现
短连接 VS 长连接 什么是短连接 客户端和服务器每进行一次HTTP操作,就建立一次连接,任务结束就中断连接。 长连接 客户端和服务器之间用于传输HTTP数据的TCP连接不会关闭,客户端再次访问这个服务器时,会继续使用这一条已经建立…...
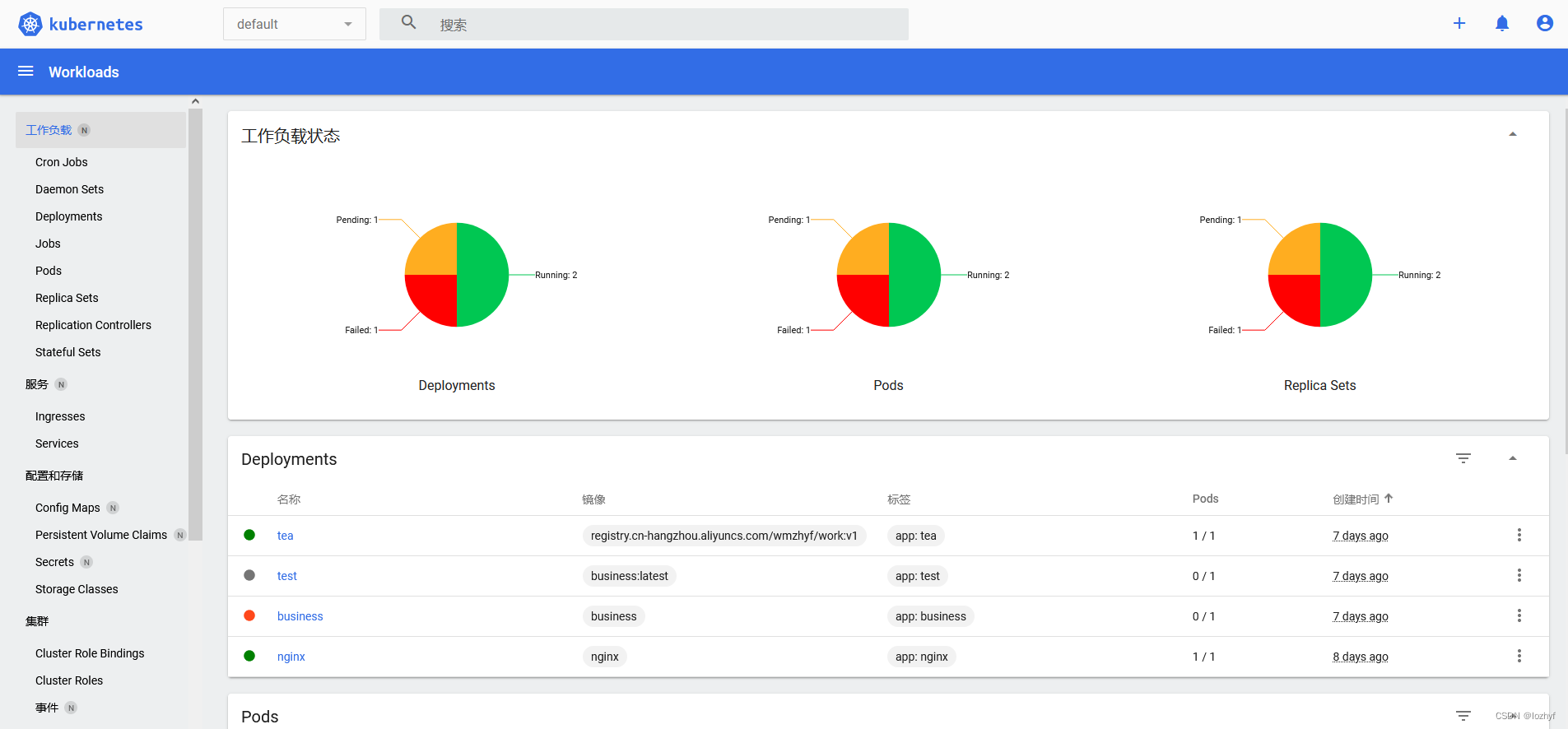
k8s 安装部署
一,准备3台机器,安装docker,kubelet、kubeadm、kubectl firewall-cmd --state 使用下面命令改hostname的值:(改为k8s-master01)另外两台改为相应的名字。 172.188.32.43 hostnamectl set-hostname k8s-master01 172.188.32.4…...
模型,IP和TCP到底在哪层?)
TCP/IP五层(或四层)模型,IP和TCP到底在哪层?
文章目录 前言一、应用层二.传输层三.网络层:四.数据链路层五.物理层:六.OSI七层模型:1.物理层(Physical Layer):2.数据链路层(Data Link Layer):3.网络层(Ne…...

STM32串口接收不定长数据(空闲中断+DMA)
玩转 STM32 单片机,肯定离不开串口。串口使用一个称为串行通信协议的协议来管理数据传输,该协议在数据传输期间控制数据流,包括数据位数、波特率、校验位和停止位等。由于串口简单易用,在各种产品交互中都有广泛应用。 但在使用串…...

LeetCode56. Merge Intervals
文章目录 一、题目二、题解 一、题目 Given an array of intervals where intervals[i] [starti, endi], merge all overlapping intervals, and return an array of the non-overlapping intervals that cover all the intervals in the input. Example 1: Input: interva…...

【华为OD题库-083】玩牌高手-Java
题目 给定一个长度为n的整型数组,表示一个选手在n轮内可选择的牌面分数。选手基于规则选牌,请计算所有轮结束后其可以获得的最高总分数。 选择规则如下: 1.在每轮里选手可以选择获取该轮牌面,则其总分数加上该轮牌面分数,为其新的…...

ARM day3
题目:实现3盏灯的流水 代码: .text .global _start _start: 设置RCC寄存器使能 LDR R0,0X50000A28 LDR R1,[R0] ORR R1,R1,#(0X1<<4) ORR R1,R1,#(0X1<<5) STR R1,[R0]设置PE10管脚为输出模式 LDR R0,0X50006000 LDR R1,[R0] BIC R1,R1,…...

[足式机器人]Part2 Dr. CAN学习笔记-自动控制原理Ch1-2稳定性分析Stability
本文仅供学习使用 本文参考: B站:DR_CAN Dr. CAN学习笔记-自动控制原理Ch1-2稳定性分析Stability 0. 序言1. 稳定的分类2. 稳定的对象3. 稳定的系统4. 系统稳定性的讨论5. 补充内容——Transfer Function(传递函数) - nonzero Initial Condition(非零初始…...
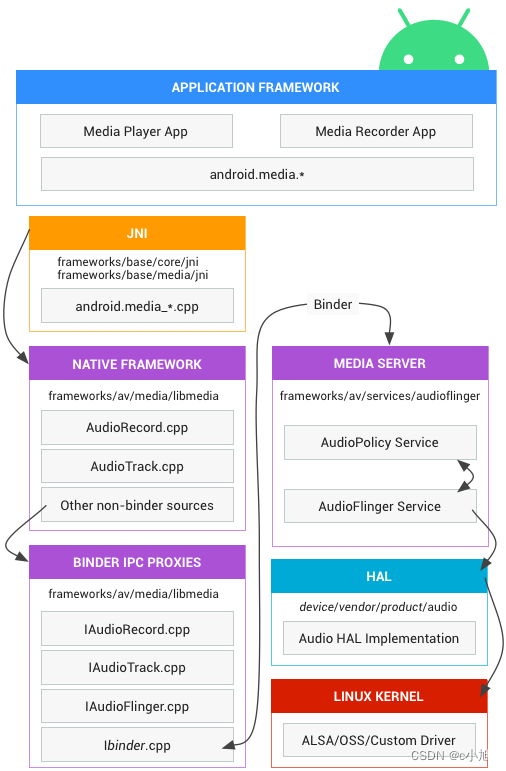
Android Audio实战——音频链路分析(二十五)
在 Android 系统的开发过程当中,音频异常问题通常有如下几类:无声、调节不了声音、爆音、声音卡顿和声音效果异常(忽大忽小,低音缺失等)等。尤其声音效果这部分问题通常从日志上信息量较少,相对难定位根因。想要分析此类问题,便需要对声音传输链路有一定的了解,能够在链…...

PHP基础 - 常量字符串
常量 在PHP中,常量是一个简单值的标识符,定义后默认是全局变量,可以在整个运行的脚本的任何地方使用。常量由英文字母、下划线和数字组成,但数字不能作为首字母出现。 PHP中定义常量的方式是使用define()函数,其语法如下: bool define( string $name, mixed $value [,…...
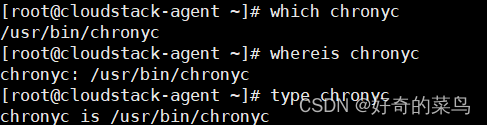
Linux查看命令的绝对路径
linux查看命令的绝对路径 在Linux中,可以使用以下命令来查看命令的绝对路径: 1、which 命令名 例如,要查看chronyc命令的绝对路径,可以运行: which chronyc 2、whereis 命令名 例如,要查看chronyc命令…...

Docker build 无法解析域名
### 报错 Docker build 无法解析域名 报错:ERROR [ 2/12] RUN curl -o /etc/yum.repos.d/CentOS-Base.repo https://mirrors.aliyun.com/repo/Centos-7.repo 解决Docker build无法解析域名 # 追加到 etc/docker/daemon.json,注意JSON的格式 {"dn…...
退稿论文重复率太高会怎么样【保姆教程】
大家好,今天来聊聊退稿论文重复率太高会怎么样,希望能给大家提供一点参考。 以下是针对论文重复率高的情况,提供一些修改建议和技巧: 退稿论文重复率太高会怎么样 在学术出版领域,论文的重复率是衡量其原创性和学术诚…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
