【C++】讲的最通透最易懂的关于结构体内存对齐的问题
目录
- 1. 内存对齐规则
- 2. 简单易懂的内存对齐示例
- 2.1 简单结构体
- 2.2 含位域的结构体
- 2.3 空类的大小
- 2.4 嵌套结构体
- 3. 为什么需要内存对齐?
- 4. 类型在不同系统下所占字节数
1. 内存对齐规则
- 第一个成员在与结构体变量偏移量为0的位置处。
- 其他成员变量要对齐到某个数字(对其数)的整数倍的地址处。对其数=编译器默认的一个对齐数与该成员大小的较小者。
vs中默认的值是8 Linux中默认的值是4 - 结构体总大小为最大对其数(每一个成员变量都有一个对其数)的整数倍。
- 如果嵌套了结构体对齐到自己的最大对其数是整数倍处,结构体的整体大小就是最大对齐数(含嵌套结构体的对齐数)的整数倍。
- 如对内存对齐有明确要求,可用
#pragma pack(n)指定(n必须是2的N次方),以n和结构体中最长数据成员长度中较小者为有效值
可能只看上面的描述你还是有点搞不懂,那么我们可以看一下具体的例子和视图讲解:
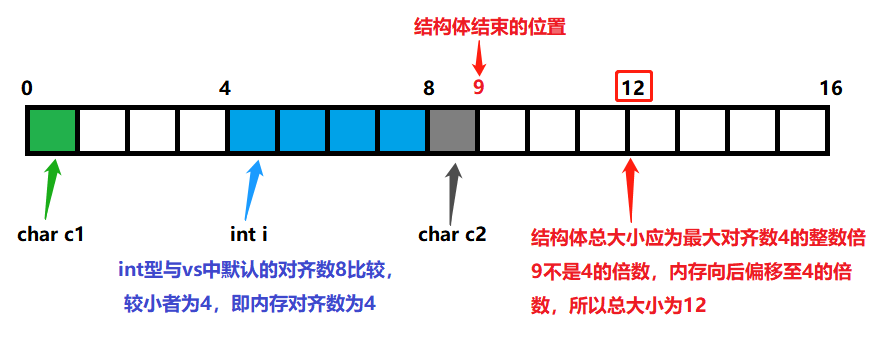
struct s1{char c1;int i;char c2;
};
//结构体总大小为:12
2. 简单易懂的内存对齐示例
2.1 简单结构体
struct s1
{char str; //1字节short x; //2字节int num; //4字节
};
// sizeof(s1) = 8 // (1+1) + 2 + 4 = 8 第2个加1处的内存是空的
2.2 含位域的结构体
一个位域必须存储在同一个字节中,不能跨两个字节。如一个字节所剩空间不够存放另一位域时,应从下一单元起存放该位域。
struct s2
{unsigned char a:7; //字段a占用了一个字节的7个bitunsigned char b:2; //字段b占用了2个bitunsigned char c:7; //字段c占用了7个bit
}s1;
// sizeof(s1) = 3 // 1 + 1 + 1 = 3
struct s3
{char t : 4; //4表示在一个字节中占4个比特位char k : 4;
};
// sizeof(s3) = 1 //0.5 + 0.5 = 1
struct s4
{char t : 4; //4表示在一个字节中占4个比特位char k : 4;unsigned short i : 8;char a;
};
// sizeof(s4) = 6 //(0.5 + 0.5 + 1) + 2 + (1+1) = 6
// 解释:0.5和0.5占一个字节,两个占4比特的刚好可以放在一个字节中,short为2字节,对齐数是2,所以0.5 + 0.5 + 1中加的1是空的
2.3 空类的大小
class A {};
// sizeof(A) = 1
空类,没有任何成员变量和成员函数,编译器是支持空类实例化对象的,对象必须要被分配内存空间才有意义,大小: 1Byte (字节)
2.4 嵌套结构体
class A {
private:double dd;int ii;int* pp;
};class Test {
private:int i;A a;double d;char* p;
};
int main()
{A a1;Test test;cout << sizeof(a1) << endl;cout << sizeof(test) << endl;
}
// x86(32位操作系统)平台运行结果:40
// x64(64位操作系统)平台运行结果:48
对其数 = 编译器默认的一个对齐数与该成员大小的较小者,vs中默认的值是8
-
x86:指针是4字节,类A的大小是16,8与16的较小者是8。内存大小为:8 + 16 + 8 + 4 = 36,又因为36不是最大对齐数8的倍数,所以内存向后偏移,大小为 40
-
x64:指针是8字节,类A大小为24,8与24的较小者是8。内存大小为:8 + 24 + 8 +8 = 48,48刚好是最大对齐数8的倍数,所以内存大小为48
3. 为什么需要内存对齐?
字节对齐主要是为了提高内存的访问效率
cpu一次能读取多少内存要看数据总线是多少位,如果是16位,则一次只能读取2个字节,如果是32位,则可以读取4个字节,并且cpu不能跨内存区间访问。
假设有这样一个结构体如下:
struct s
{char a;int b;
};
假设地址空间是类似下面这样的:

-
在没有字节对齐的情况下,变量a就是占用了
0x00000001这一个字节,而变量b则是占用了0x00000002~0x000000005这四个字节,那么cpu如果想从内存中读取变量b,首先要从变量b的开始地址0x00000002读到0x0000004,然后再读取一次0x00000005这个字节,相当于读一个int,cpu从内存读取了两次。 -
而如果进行字节对齐的话,变量a还是占用了
0x00000001这一个字节,而变量b则是占用了0x00000005~0x00000008这四个字节,那么cpu要读取变量b的话,就直接一次性从0x00000005读到0x00000008,就一次全部读取出来了。 -
所以说,字节对齐的根本原因其实在于cpu读取内存的效率问题,对齐以后,cpu读取内存的效率会更快。结构体的内存对齐是拿空间来换取时间的做法
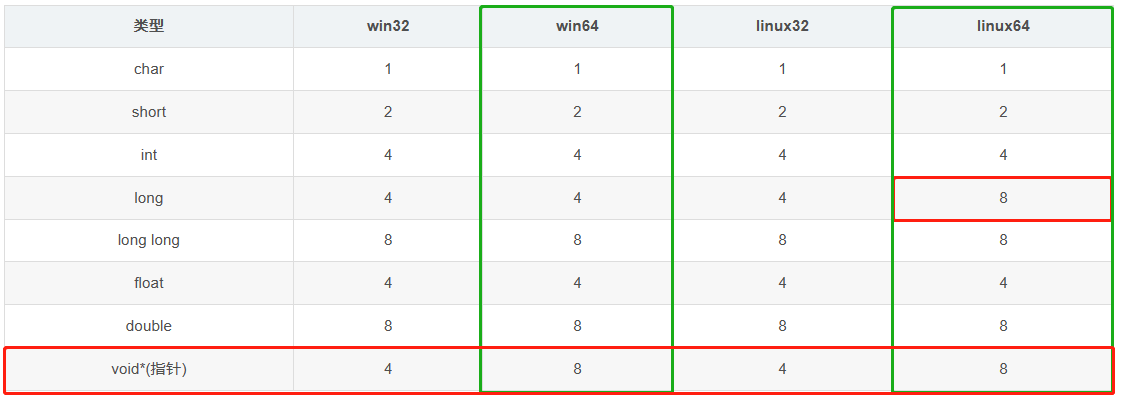
4. 类型在不同系统下所占字节数
| 类型 | win32 | win64 | linux32 | linux64 |
|---|---|---|---|---|
| char | 1 | 1 | 1 | 1 |
| short | 2 | 2 | 2 | 2 |
| int | 4 | 4 | 4 | 4 |
| long | 4 | 4 | 4 | 8 |
| long long | 8 | 8 | 8 | 8 |
| float | 4 | 4 | 4 | 4 |
| double | 8 | 8 | 8 | 8 |
| void*(指针) | 4 | 8 | 4 | 8 |
相关文章:

【C++】讲的最通透最易懂的关于结构体内存对齐的问题
目录1. 内存对齐规则2. 简单易懂的内存对齐示例2.1 简单结构体2.2 含位域的结构体2.3 空类的大小2.4 嵌套结构体3. 为什么需要内存对齐?4. 类型在不同系统下所占字节数1. 内存对齐规则 第一个成员在与结构体变量偏移量为0的位置处。其他成员变量要对齐到某个数字&a…...
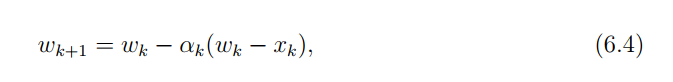
Stochastic Approximation 随机近似方法的详解之(一)
随机近似的定义:它指的是一大类随机迭代算法,用于求根或者优化问题。 Stochastic approximation refers to a broad class of stochastic iterative algorithms solving root finding or optimization problems. temporal-difference algorithms是随机近…...

软件自动化测试工程师面试题集锦
以下是部分面试题目和我的个人回答,回答比较简略,仅供参考。不对之处请指出 1.自我介绍 答:姓名,学历专业,技能,近期工作经历等,可以引导到最擅长的点,比如说代码或者项目 参考&a…...

智合同丨教你做一个懂AI的法律人
作为一名法律人,合同审核工作是日常工作中最基本也是必不可少的一项事务。我们知道,一般在企业,合同审批会涉及到众多部门和职务角色,最关键的一环其实在法务或者律师建议,其他部门给出的审批意见基本上都是基于自己部…...

如何判断自己使用的IP是独享还是共享?
在互联网上,我们常常听到独享IP和共享IP这两个概念。独享IP指的是一个IP地址只被一个用户或一个网站所使用,而共享IP则是多个用户或多个网站共用一个IP地址。那么,如何分辨IP是不是独享呢?接下来,我们将从几个方面来看。在这之前…...

跳石头
题目描述 一年一度的"跳石头"比赛又要开始了! 这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间,有 N 块岩石(不含起点和终点的岩石)。在比赛过程中,选手们将从起点出发,每一步跳…...
上传gitee教程,Gitee怎么上传代码到仓库
目录 第一步:配置git的用户名和邮箱 第二步:上传到远程仓库 第三步:将仓库的master分支拉取过来和本地的当前分支进行合并 第四步:将修改的所有代码添加到暂存区 第五步:将缓存区内容添加到本地仓库(…...

netstat命令详解
1、下载netstat命令对应的软件包 yum install net-tools -y2、netsta命令介绍 [rootvm01 ~]# man netstatNETSTAT(8) Linux System Administrators Manual NETSTAT(8)NAMEnetstat - Print network connections, routing t…...

数据库三范式
文章目录数据库三范式1. 第一范式(1NF)2. 第二范式(2NF)3. 第三范式(3NF)数据库三范式 第一范式:有主键,具有原子性,字段不可分割第二范式:完全依赖…...

K8S 1.20 弃用 Docker 评估之 Docker 和 OCI 镜像格式的差别
背景 2020 年 12 月初,Kubernetes 在其最新的 Changelog 中宣布,自 Kubernetes 1.20 之后将弃用 Docker 作为容器运行时。 弃用 Docker 带来的,可能是一系列的改变,包括不限于: 容器镜像构建工具容器 CLI容器镜像仓…...

Vue2和Vue3响应式的区别
数据响应式是什么? 所谓 数据响应式 就是建立 响应式数据 与 依赖(调用了响应式数据的操作)之间的关系,当响应式数据发生变化时,可以通知那些使用了这些响应式数据的依赖操作进行相关更新操作,可以是DOM…...

模型实战(6)之Alex实现图像分类:模型原理+训练+预测(详细教程!)
Alex实现图像分类:模型原理+训练+预测 图像分类或者检索任务在浏览器中的搜索操作、爬虫搜图中应用较广,本文主要通过Alex模型实现猫狗分类,并且将可以复用的开源模型在文章中给出!!!数据集可以由此下载:Data本文将从以下内容做出讲述: 1.模型简介及环境搭建2.数据集准…...

【大数据】最全的大数据Hadoop|Yarn|Spark|Flink|Hive技术书籍分享/下载链接,持续更新中...
这里写目录标题Hadoop大数据处理Hadoop技术内幕:深入解析YARN架构设计与实现原理Hadoop 技术内幕:深入解析Hadoop Common 和HDFS 架构设计与实现原理Spark SQL内核剖析Hadoop 应用架构深度剖析Hadoop HDFSHadoop实战Hive编程指南Hadoop大数据处理 本书以…...

RIG Exploit Kit 仍然通过 IE 感染企业用户
RIG Exploit Kit 正处于最成功的时期,每天尝试大约 2000 次入侵并在大约 30% 的案例中成功,这是该服务长期运行历史中的最高比率。 通过利用相对较旧的 Internet Explorer 漏洞,RIG EK 已被发现分发各种恶意软件系列,包括 Dridex…...
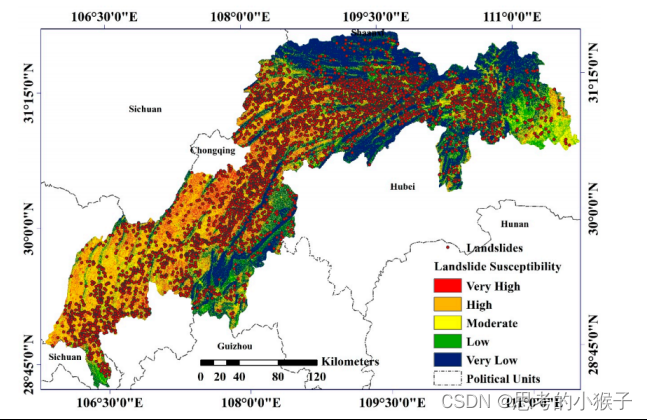
GIS在地质灾害危险性评估与灾后重建中的实践技术应用及python机器学习灾害易发性评价模型建立与优化进阶
地质灾害是指全球地壳自然地质演化过程中,由于地球内动力、外动力或者人为地质动力作用下导致的自然地质和人类的自然灾害突发事件。由于降水、地震等自然作用下,地质灾害在世界范围内频繁发生。我国除滑坡灾害外,还包括崩塌、泥石流、地面沉…...

SQL SERVER中SCHEMA的詳解
SQL SERVER中SCHEMA的講解1. Introduction1.1 優勢1.2 內置schema2. Create Schema2.1 Parameters2.2 Sql3.Awakening1. Introduction 1.1 優勢 数据库模式为我们提供了在数据库中创建逻辑对象组的灵活性。如果多个团队使用同一个数据库,我们可以设计各种模式来分組…...
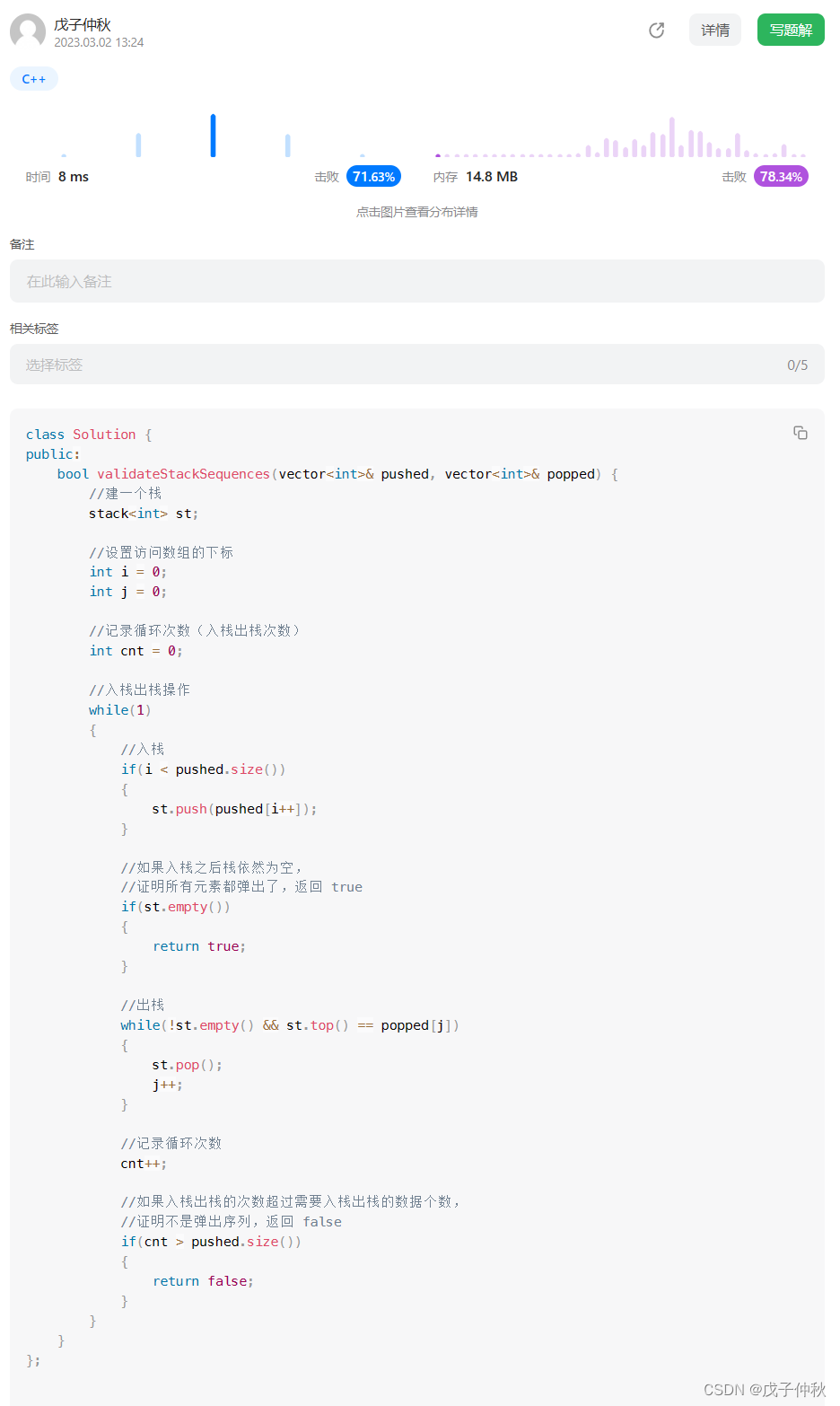
【LeetCode】剑指 Offer(13)
目录 题目:剑指 Offer 31. 栈的压入、弹出序列 - 力扣(Leetcode) 题目的接口: 解题思路: 代码: 过啦!!! 写在最后: 题目:剑指 Offer 31. 栈…...

帮助小型企业实现业务增长的7种数字营销策略
数字营销一直在不断地变化和发展,在过去的几年里我们已经见识到了其迅猛的发展速度。虽然我们在数字营销中看到了一些新的趋势,但对于小型企业来说很难利用并发挥其优势。相比较大型企业,小型企业的预算和资源通常有限,所以他们很…...

互联网行业的高级产品经理和普通产品经理有哪些区别?
普通产品经理的一天可能是这样的。 早上到公司想一想,这几天有哪些事情要处理。打开记事本,按照上面要求的任务一条一条开始做。 这里有个需求,是要给产品的聊天模块增加历史记录。嗯,看一下常见的几款社交工具 APP,他…...

aardio - 【库】简单信息框
昨晚得知aardio作者一鹤的妻子病情严重,深感悲痛。今日给一鹤捐赠少许,望其妻能挺过难关,早日康复。 aardio是一个很好的编程工具,我非常喜欢,这两年也一直在用。虽然未曾用其获利,但其灵活的语法ÿ…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

沙箱虚拟化技术虚拟机容器之间的关系详解
问题 沙箱、虚拟化、容器三者分开一一介绍的话我知道他们各自都是什么东西,但是如果把三者放在一起,它们之间到底什么关系?又有什么联系呢?我不是很明白!!! 就比如说: 沙箱&#…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...
