当前位置： 首页 > news >正文

UG NX二次开发(C#)-求曲线在某一点处的法矢和切矢

news 2026/2/10 20:31:50

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

文章目录

  • 1、前言
  • 2、在UG NX中创建一个曲线
  • 3、直接放代码
  • 4、测试案例

1、前言

最近确实有点忙了，好久没更新博客了。今天恰好有时间，就更新下，还请家人们见谅。
今天我们讲一下如何获取一条曲线上某一条曲线上的切向量和法向量。

2、在UG NX中创建一个曲线

如下图所示，这条曲线是样条曲线。
在这里插入图片描述
我们以这条曲线上的中点为例，计算此点处的切矢量和法矢量。

3、直接放代码

if(block == edge_select0

相关文章：

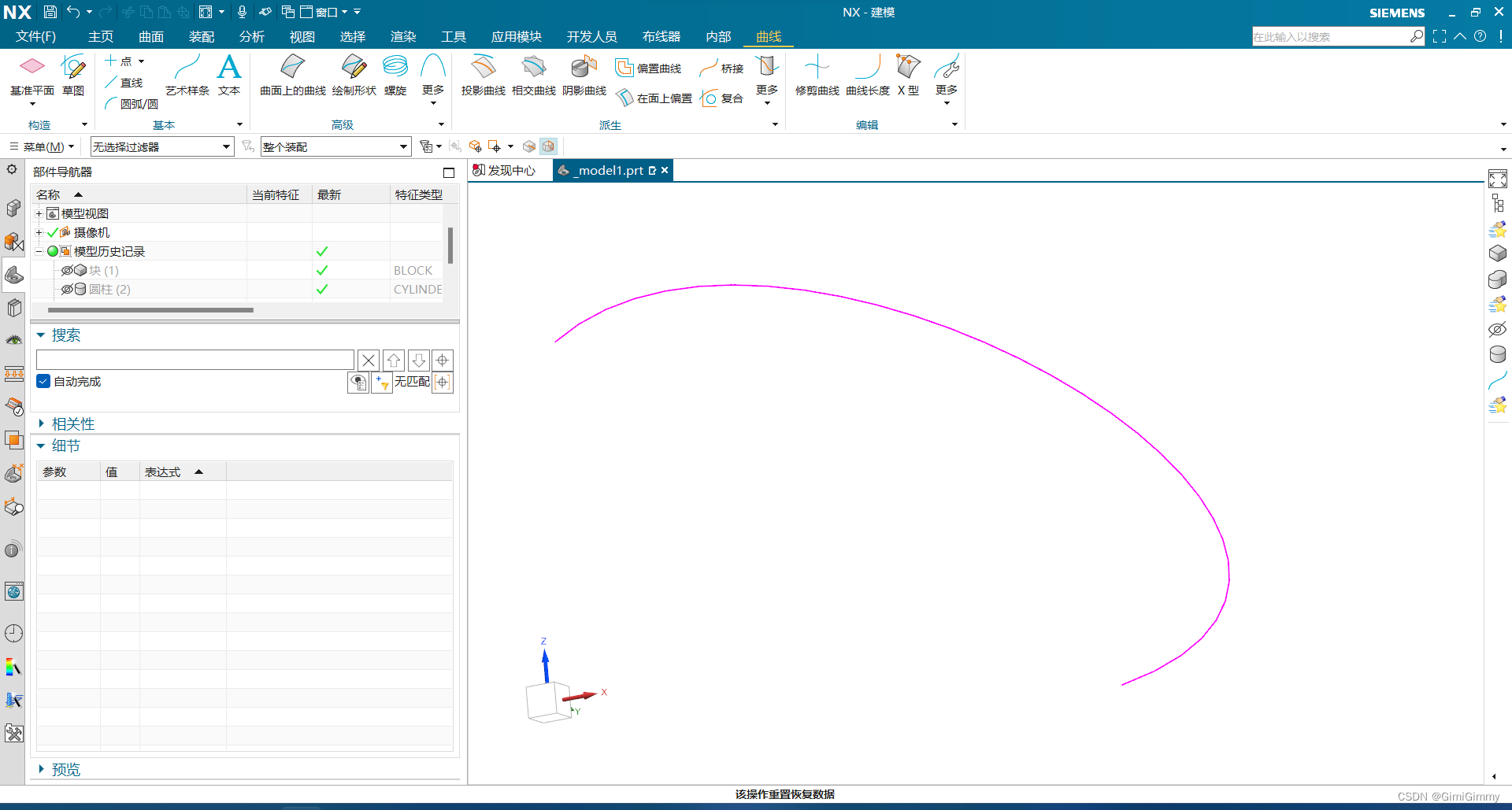
UG NX二次开发(C#)-求曲线在某一点处的法矢和切矢

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档 文章目录 1、前言2、在UG NX中创建一个曲线3、直接放代码4、测试案例1、前言 最近确实有点忙了，好久没更新博客了。今天恰好有时间，就更新下，还请家人们见谅。 今天我们讲一下如何获取一条曲线上某一条曲…...

编程日记 2023/12/12 1:07:30

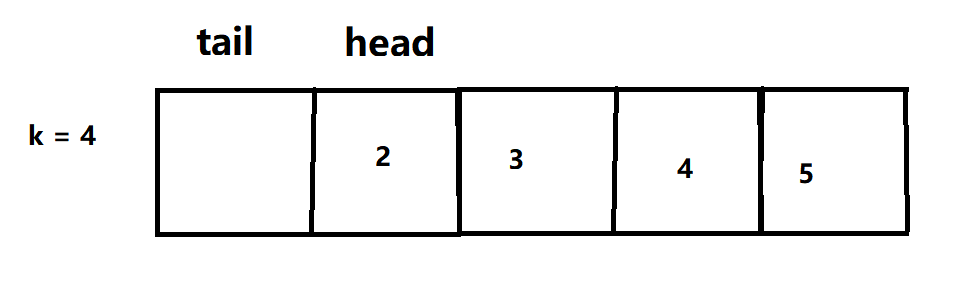
leetcode 622. 设计循环链表

这道题讲了两种方法，第一个代码是用数组实现的，第二个是用链表实现的，希望对你们有帮助 （最好在VS自己测试一遍，再放到 leetcode上哦） 下面的是主函数（作参考），静下心来…...

编程日记 2023/12/12 1:06:29

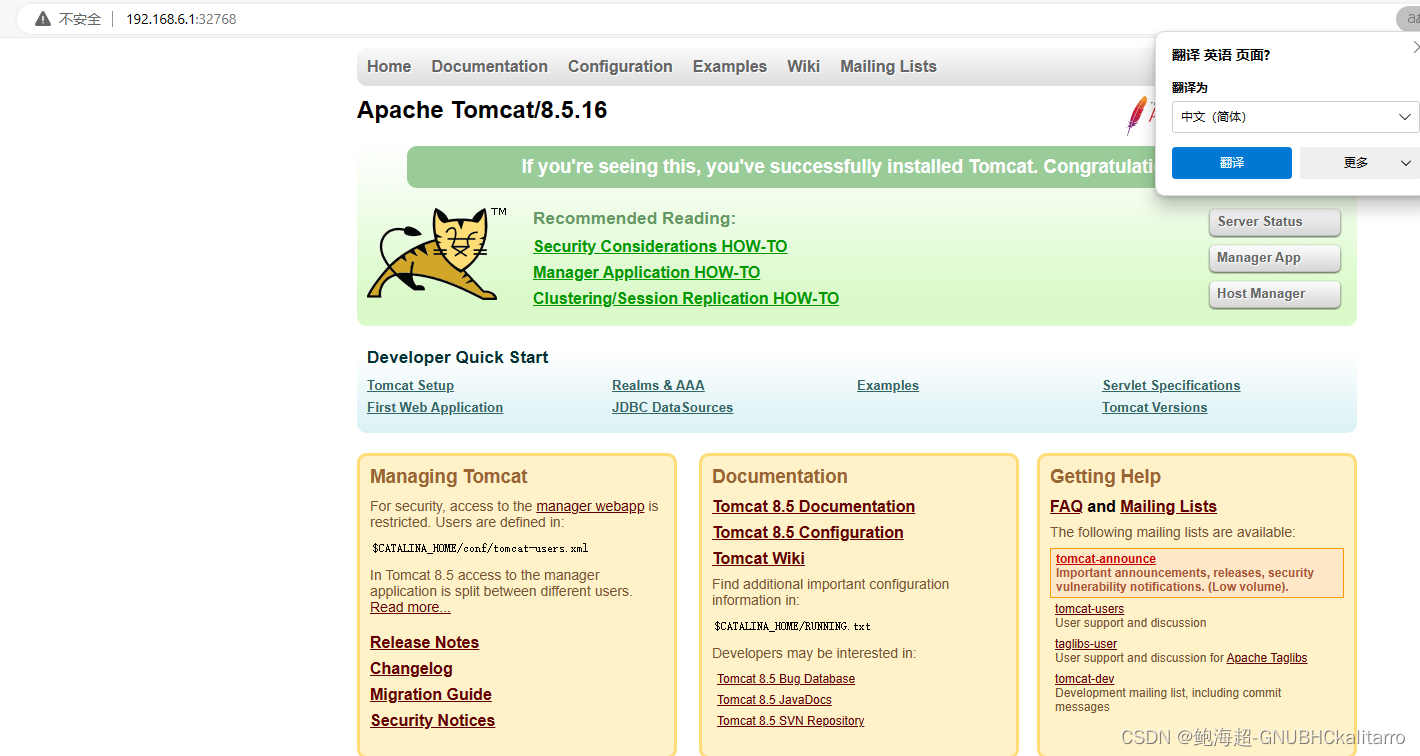
Linux：dockerfile编写搭建tomcat练习（9）

我使用的httpyum仓库 本地使用了5个文件，tomcat使用的官网解压直接用的包】 Dockerfile 主配置文件 基于centos基础镜像 jdk1.8.0_91 java环境 run.sh 启动脚本 centos.repo 仓库文件 tomcat 源码包 vim Dockerfile写入FROM centos MAINTAINER ta…...

编程日记 2023/12/12 1:03:27

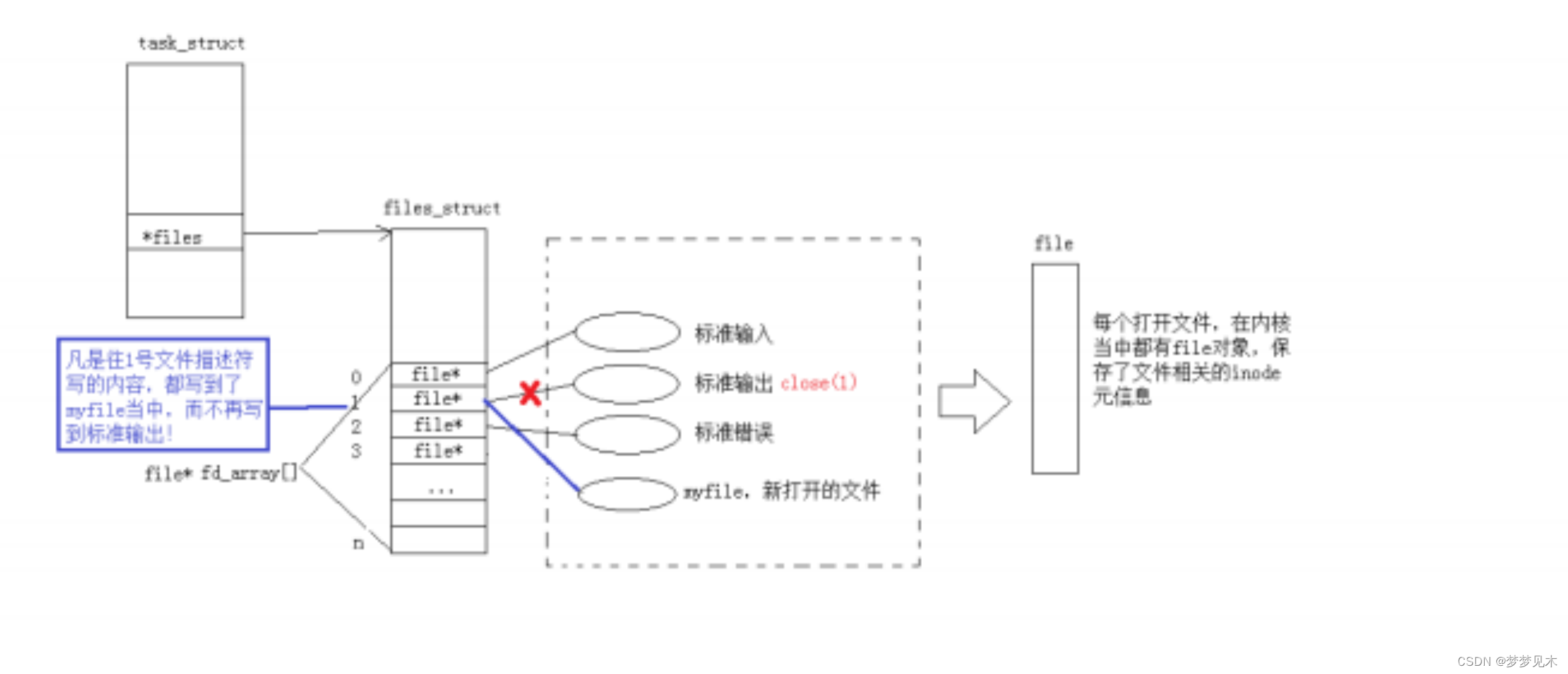
Linux 基础IO

文章目录 前言基础IO定义系统IO接口文件描述符重定向原理缓冲区刷新 前言 要知道每个函数/接口的全部参数和返回值建议去官网或者直接在Linux的man手册中查，这不是复制粘贴函数用法的文章。 C语言文件读写介绍链接 基础IO定义 IO是Input/Output的缩写&#xff0c…...

编程日记 2023/12/12 1:02:26

uniapp 打开文件管理器上传(H5、微信小程序、android app三端)文件

H5跟安卓APP 手机打开的效果图&#xff1a; Vue页面&#xff1a; <template><view class"content"><button click"uploadFiles">点击上传</button></view> </template><script>export default {data() {return…...

编程日记 2023/12/12 0:58:23

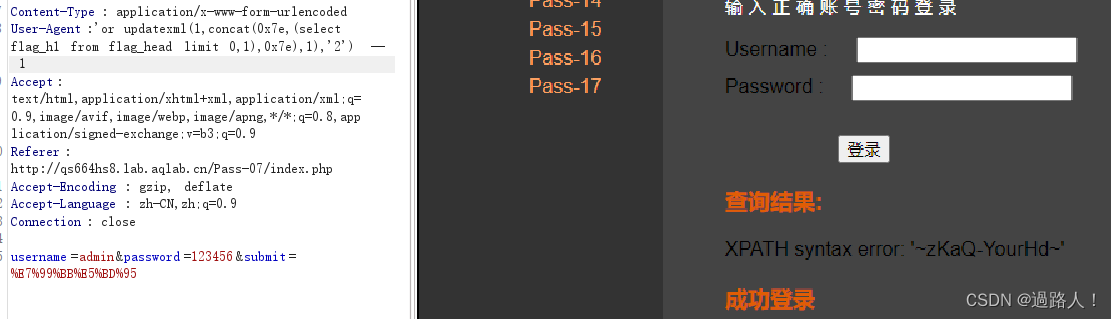
掌控安全 -- header注入

http header注入 该注入是指利用后端验证客户端口信息&#xff08;比如常用的cookie验证&#xff09;或者通过http header中获取客户端的一些信息&#xff08;比如useragent用户代理等其他http header字段信息&#xff09;&#xff0c;因为这些信息是会重新返回拼接到后台中的&…...

编程日记 2023/12/12 0:55:20

windows批处理脚本（.bat）如何激活Anconda Prompt虚拟环境

通过call 来调用激活脚本&#xff0c; activate myenv指的是要激活的环境&#xff0c;若省略&#xff0c;则激活的是base环境。 call : 从另一个批处理程序调用一个批处理程序&#xff0c;而不停止父批处理程序。 call C:\ProgramData\Anaconda3\Scripts\activate.bat activate…...

编程日记 2023/12/12 0:53:18

扩散模型实战（十四）：扩散模型生成音频

推荐阅读列表&#xff1a; 扩散模型实战&#xff08;一&#xff09;&#xff1a;基本原理介绍 扩散模型实战&#xff08;二&#xff09;&#xff1a;扩散模型的发展 扩散模型实战&#xff08;三&#xff09;&#xff1a;扩散模型的应用 扩散模型实战&#xff08;四&#xff…...

编程日记 2023/12/12 0:52:17

《微信小程序开发从入门到实战》学习四十七

4.4 云函数 4.4.5 云函数的定时触发 如果云函数需要定时执行&#xff0c;可以使用云函数定时触发器。配置了定时触发器&#xff0c;云函数会在相应时间点被自动触发。函数返回结果不会返回调用方 在需要添加触发器的云函数下新建文件config.json。格式如下&#xff1a; &quo…...

编程日记 2023/12/12 0:51:17

LeetCode刷题笔记之数组

一、二分查找 1. 704【二分查找】 题目&#xff1a; 给定一个 n 个元素 有序的&#xff08;升序&#xff09; 整型数组 nums 和一个目标值 target &#xff0c;写一个函数搜索 nums 中的 target&#xff0c;如果目标值存在返回下标&#xff0c;否则返回 -1。代码&#xff1a;…...

编程日记 2023/12/12 0:48:14

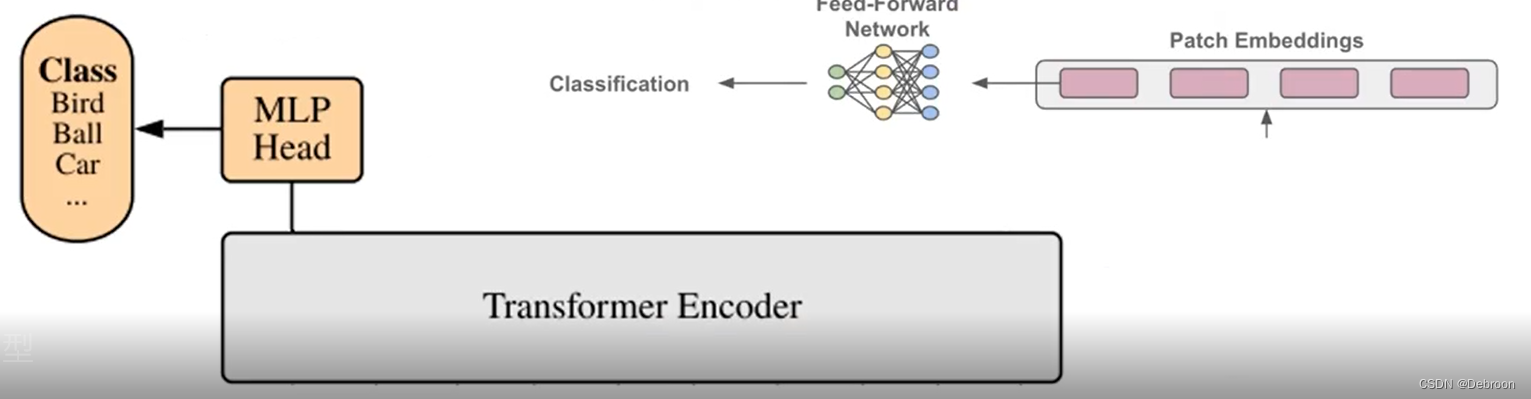
ViT：视觉 Transformer

ViT&#xff1a;视觉 Transformer 网络结构Transformer 编码器MLP 头CNN 和 Transformer 网络结构 Transformer 的优势&#xff1a;注意力机制相当于一个多标签检索系统&#xff0c;位置嵌入能知道每个单词的位置&#xff0c;而且适合并行。 尝试把 Transformer 迁移到视觉领…...

编程日记 2023/12/12 0:47:13

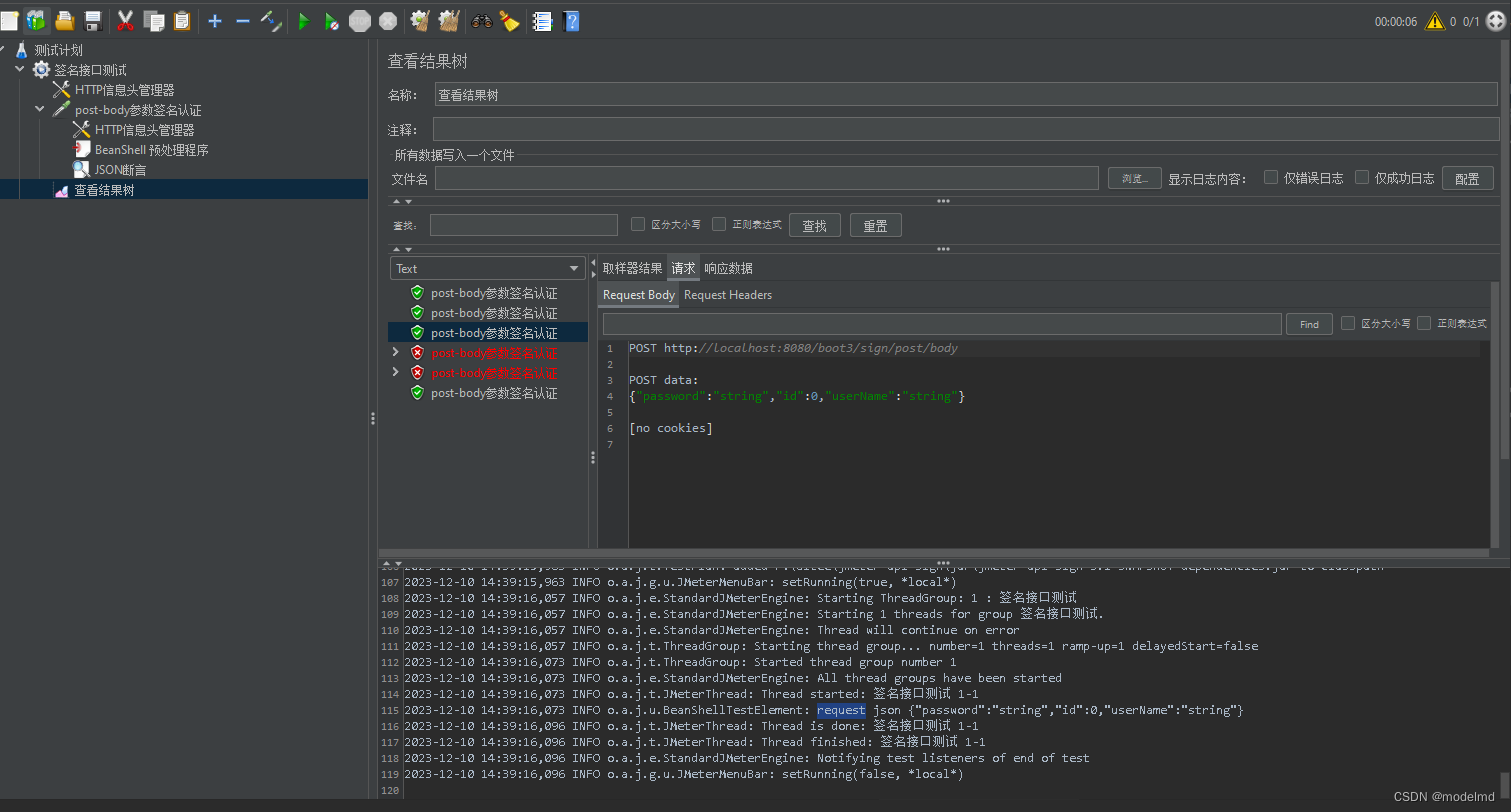
Jmeter 请求签名api接口-BeanShell

Jmeter 请求签名api接口-BeanShell 项目签名说明编译扩展jar包jmeter 使用 BeanShell 调用jar包中的签名方法 项目签名说明 有签名算法的api接口本地不好测试&#xff0c;使用BeanShell 扩展jar 包对参数进行签名&#xff0c;接口签名算法使用 sha512Hex 算法。签名的说明如下…...

编程日记 2023/12/12 0:46:12

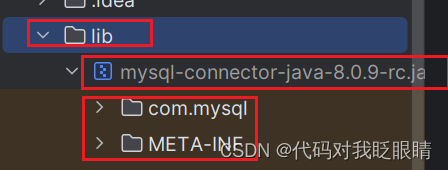
No suitable driver found for jdbc:mysql://localhost:3306（2023/12/7更新）

有两种情况&#xff1a; 压根没安装下载了但没设为库或方法不对 大多数为第一种情况&#xff1a; 一. 下载jdbc 打开网址选择一个版本进行下载 https://nowjava.com/jar/version/mysql/mysql-connector-java.html 二.安装jdbc 在项目里建一个lib文件夹 在把之前下载的jar文…...

编程日记 2023/12/12 0:42:09

word文档中数字格式转换（排版助手）

示例&#xff1a;李老师收入了234243.33元&#xff0c;产量3000公斤&#xff1b; 张老师收入了2324324元&#xff0c;产量45555公斤&#xff1b; 孙老师收入了600000元&#xff0c;产量2342公斤 王老师收入了1234443243元&#xff0c;产量1243142公斤。 1、数字批量转换成千…...

编程日记 2023/12/12 0:41:08

阿里云docker加速

文章目录 一、 阿里云镜像仓库配置二、配置加速1. CentOS2. Mac3. Windows注意 一、 阿里云镜像仓库配置 1.注册阿里云账号&#xff0c;并登陆到阿里云后台&#xff0c;进入控制台面板 2.进入控制台以后&#xff0c;找到左上方的三横的功能列表按钮&#xff0c;在弹出来的功能…...

编程日记 2023/12/12 0:40:06

Panalog 日志审计系统 sprog_deletevent.php SQL 注入漏洞复现

0x01 产品简介 Panalog大数据日志审计系统定位于将大数据产品应用于高校、 公安、 政企、 医疗、 金融、 能源等行业之中&#xff0c;针对网络流量的信息进行日志留存&#xff0c;可对用户上网行为进行审计&#xff0c;逐渐形成大数据采集、 大数据分析、 大数据整合的工作模式…...

编程日记 2023/12/12 0:39:05

openGauss学习笔记-152 openGauss 数据库运维-备份与恢复-物理备份与恢复之PITR恢复

文章目录 openGauss学习笔记-152 openGauss 数据库运维-备份与恢复-物理备份与恢复之PITR恢复152.1 背景信息152.2 前提条件152.3 PITR恢复流程152.4 recovery.conf文件配置**152.4.1 归档恢复配置****152.4.2 恢复目标设置** openGauss学习笔记-152 openGauss 数据库运维-备份…...

编程日记 2023/12/12 0:37:03

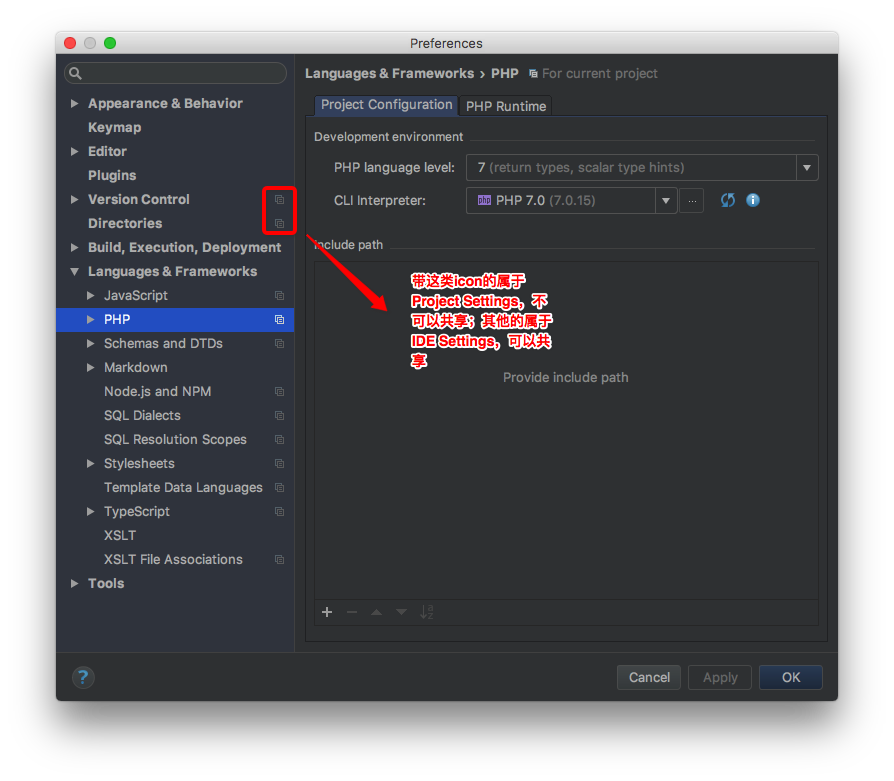
PhpStorm基本配置及常用快捷键

重要Preference配置 激活服务器 http://jetbrains.tencent.click/http://owo.helphttp://idea.imsxm.com/http://www.0-php.com:10172017.3以上版本 JetBrains IDE 2017.3以上版本&#xff0c;激活检测机制变成了动态封禁域名&#xff0c;导致大部分域名激活被屏蔽了&#xff0…...

编程日记 2023/12/12 0:35:02

Autosar通信实战系列05-CanNM模块进阶常见问题思考

本文框架 前言1. UDS 0x28服务控制Nm报文收发后对状态机有影响？2. 节点网络启动后第一帧是否必须是网络管理报文？3. 主动唤醒后发送的第一帧报文为NM报文如何配置？4. CanNmMsgCycleOffset的使用场景？5. 什么情况下CBV中RepeatMessageRequest Bit置位？6. 主动（本地）唤醒与…...

编程日记 2023/12/12 0:34:01

Java中多态的一些简单理解

什么是多态 1.面向对象的三大特性&#xff1a;封装、继承、多态。从一定角度来看&#xff0c;封装和继承几乎都是为多态而准备的。这是我们最后一个概念&#xff0c;也是最重要的知识点。 2.多态的定义&#xff1a;指允许不同类的对象对同一消息做出响应。即同一消息可以根据发…...

编程日记 2023/12/12 0:33:00

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)

题目&#xff1a;3442. 奇偶频次间的最大差值 I 思路 &#xff1a;哈希&#xff0c;时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况&#xff0c;哈希表这里用数组即可实现。 C版本&#xff1a; class Solution { public:int maxDifference(string s) {int a[26]…...

编程新知 2026/2/7 23:18:31

华为云AI开发平台ModelArts

华为云ModelArts&#xff1a;重塑AI开发流程的“智能引擎”与“创新加速器”&#xff01; 在人工智能浪潮席卷全球的2025年&#xff0c;企业拥抱AI的意愿空前高涨&#xff0c;但技术门槛高、流程复杂、资源投入巨大的现实&#xff0c;却让许多创新构想止步于实验室。数据科学家…...

编程新知 2026/2/8 4:37:19

【杂谈】-递归进化：人工智能的自我改进与监管挑战

递归进化&#xff1a;人工智能的自我改进与监管挑战 文章目录 递归进化&#xff1a;人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管&#xff1f;3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

编程新知 2025/12/9 0:22:01

iOS 26 携众系统重磅更新，但“苹果智能”仍与国行无缘

美国西海岸的夏天&#xff0c;再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至&#xff0c;这不仅是开发者的盛宴&#xff0c;更是全球数亿苹果用户翘首以盼的科技春晚。今年&#xff0c;苹果依旧为我们带来了全家桶式的系统更新&#xff0c;包括 iOS 26、iPadOS 26…...

编程新知 2026/2/8 20:41:56

.Net框架，除了EF还有很多很多......

文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

编程新知 2026/2/1 19:26:16

python如何将word的doc另存为docx

将 DOCX 文件另存为 DOCX 格式&#xff08;Python 实现&#xff09; 在 Python 中&#xff0c;你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是&#xff0c;.doc 是旧的 Word 格式&#xff0c;而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

编程新知 2025/12/13 22:42:30

python执行测试用例，allure报乱码且未成功生成报告

allure执行测试用例时显示乱码&#xff1a;‘allure’ &#xfffd;&#xfffd;&#xfffd;&#xfffd;&#xfffd;ڲ&#xfffd;&#xfffd;&#xfffd;&#xfffd;ⲿ&#xfffd;&#xfffd;&#xfffd;Ҳ&#xfffd;&#xfffd;&#xfffd;ǿ&#xfffd;&am…...

编程新知 2026/2/7 4:21:44

技术栈RabbitMq的介绍和使用

目录 1. 什么是消息队列&#xff1f;2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

编程新知 2026/2/10 6:20:58

【网络安全】开源系统getshell漏洞挖掘

审计过程&#xff1a; 在入口文件admin/index.php中&#xff1a; 用户可以通过m,c,a等参数控制加载的文件和方法&#xff0c;在app/system/entrance.php中存在重点代码&#xff1a; 当M_TYPE system并且M_MODULE include时&#xff0c;会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

编程新知 2026/1/31 2:59:25

什么是VR全景技术

VR全景技术&#xff0c;全称为虚拟现实全景技术&#xff0c;是通过计算机图像模拟生成三维空间中的虚拟世界&#xff0c;使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验&#xff0c;结合图文、3D、音视频等多媒体元素…...

编程新知 2026/2/5 19:40:10