【算法优选】 动态规划之路径问题——贰
文章目录
- 🎋前言
- 🌲[下降最小路径和](https://leetcode.cn/problems/minimum-path-sum/)
- 🚩题目描述
- 🚩算法思路:
- 🚩代码实现
- 🎍[最小路径和](https://leetcode.cn/problems/minimum-path-sum/)
- 🚩算法思路
- 🚩代码实现
- 🌴[地下城游戏](https://leetcode.cn/problems/dungeon-game/)
- 🚩题目描述
- 🚩算法思路
- 🚩代码实现
- ⭕总结
🎋前言
动态规划相关题目都可以参考以下五个步骤进行解答:
-
状态表⽰
-
状态转移⽅程
-
初始化
-
填表顺序
-
返回值
后面题的解答思路也将按照这五个步骤进行讲解。
🌲下降最小路径和
🚩题目描述
给你一个 n x n 的 方形 整数数组 matrix ,请你找出并返回通过 matrix 的下降路径 的 最小和 。
下降路径 可以从第一行中的任何元素开始,并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列(即位于正下方或者沿对角线向左或者向右的第一个元素)。具体来说,位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。
- 示例 1:
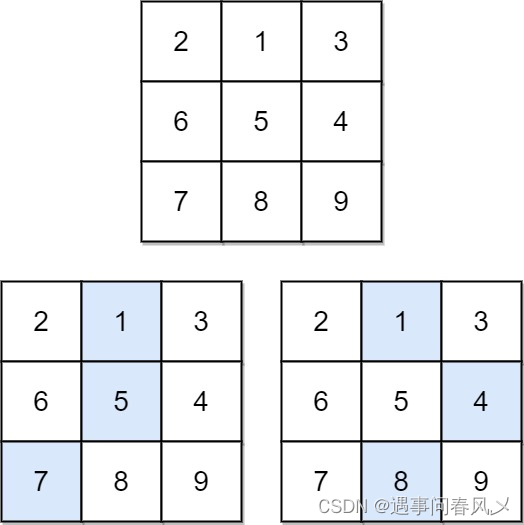
输入:matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出:13
解释:如图所示,为和最小的两条下降路径
- 示例 2:
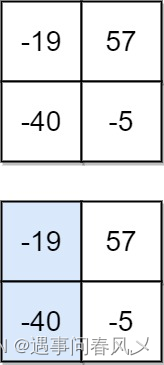
输入:matrix = [[-19,57],[-40,-5]]
输出:-59
解释:如图所示,为和最小的下降路径
class Solution {public int minFallingPathSum(int[][] matrix) {}
}
🚩算法思路:
关于这⼀类题,由于我们做过类似的,因此「状态表⽰」以及「状态转移」是⽐较容易分析出来的。
⽐较难的地⽅可能就是对于「边界条件」的处理。
- 状态表⽰:
对于这种「路径类」的问题,我们的状态表⽰⼀般有两种形式:- 从 [i, j] 位置出发,到达⽬标位置有多少种⽅式;
- 从起始位置出发,到达 [i, j] 位置,⼀共有多少种⽅式
这⾥选择第⼆种定义状态表⽰的⽅式:
dp[i][j] 表⽰:到达 [i, j] 位置时,所有下降路径中的最⼩和。
- 状态转移⽅程:
对于普遍位置 [i, j] ,根据题意得,到达 [i, j] 位置可能有三种情况:- 从正上⽅ [i - 1, j] 位置转移到 [i, j] 位置;
- 从左上⽅ [i - 1, j - 1] 位置转移到 [i, j] 位置;
- 从右上⽅ [i - 1, j + 1] 位置转移到 [i, j] 位置;
我们要的是三种情况下的「最⼩值」,然后再加上矩阵在 [i, j] 位置的值。于是 dp[i][j] = min(dp[i - 1][j], min(dp[i - 1][j - 1], dp[i - 1][j +1])) + matrix[i][j] 。
- 初始化:
可以在最前⾯加上⼀个「辅助结点」,帮助我们初始化。使⽤这种技巧要注意两个点:- 辅助结点⾥⾯的值要「保证后续填表是正确的」;
- 「下标的映射关系」。
在本题中,需要「加上⼀⾏」,并且「加上两列」。所有的位置都初始化为⽆穷⼤,然后将第⼀⾏初始化为0 即可。
-
填表顺序:
根据「状态表⽰」,填表的顺序是「从上往下」。 -
返回值:
注意这⾥不是返回 dp[m][n] 的值!
题⽬要求「只要到达最后⼀⾏」就⾏了,因此这⾥应该返回「dp表中最后⼀⾏的最⼩值」。
🚩代码实现
class Solution {public int minFallingPathSum(int[][] matrix) {// 1. 创建 dp 表// 2. 初始化// 3. 填表// 4. 返回结果int n = matrix.length;int[][] dp = new int[n + 1][n + 2];for(int i = 1; i <= n; i++) {dp[i][0] = dp[i][n + 1] = Integer.MAX_VALUE;}for(int i = 1; i <= n; i++){for(int j = 1; j <= n; j++) {dp[i][j] = Math.min(dp[i - 1][j], Math.min(dp[i - 1][j - 1],dp[i - 1][j + 1])) + matrix[i - 1][j - 1];}}int ret = Integer.MAX_VALUE;for(int j = 1; j <= n; j++) {ret = Math.min(ret, dp[n][j]);}return ret;}
}
🎍最小路径和
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
-
示例 1:
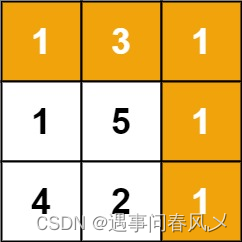
输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。 -
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
class Solution {public int minPathSum(int[][] grid) {}
}
🚩算法思路
像这种表格形式的动态规划,是⾮常容易得到「状态表⽰」以及「状态转移⽅程」的,可以归结到「不同路径」⼀类的题⾥⾯。
- 状态表⽰:
对于这种路径类的问题,我们的状态表⽰⼀般有两种形式:- 从 [i, j] 位置出发,一系列操作;
- 从起始位置出发,到达 [i, j] 位置,一系列操作。
这⾥选择第⼆种定义状态表⽰的⽅式:dp[i][j] 表⽰:到达 [i, j] 位置处,最⼩路径和是多少。
- 状态转移:
简单分析⼀下。如果 dp[i][j] 表⽰到达到达 [i, j] 位置处的最⼩路径和,那么到达[i, j] 位置之前的⼀⼩步,有两种情况:- 从 [i - 1, j] 向下⾛⼀步,转移到 [i, j] 位置;
- 从 [i, j - 1] 向右⾛⼀步,转移到 [i, j] 位置。
由于到 [i, j] 位置两种情况,并且我们要找的是最⼩路径,因此只需要这两种情况下的最⼩值,再加上 [i, j] 位置上本⾝的值即可。也就是: dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]
- 初始化:
可以在最前⾯加上⼀个「辅助结点」,帮助我们初始化。使⽤这种技巧要注意两个点:- 辅助结点⾥⾯的值要「保证后续填表是正确的」;
- 「下标的映射关系」。
在本题中,「添加⼀⾏」,并且「添加⼀列」后,所有位置的值可以初始化为⽆穷⼤,然后让dp[0][1] = dp[1][0] = 1 即可。
-
填表顺序:
根据「状态转移⽅程」的推导来看,填表的顺序就是「从上往下」填每⼀⾏,每⼀⾏「从左往后」。 -
返回值:
根据「状态表⽰」,我们要返回的结果是 dp[m][n]
🚩代码实现
class Solution {public int minPathSum(int[][] grid) {// 1. 创建 dp 表// 2. 初始化// 3. 填表// 4. 返回值int m = grid.length;int n = grid[0].length;int[][] dp = new int[m + 1][n + 1];for(int j = 0; j <= n; j++) {dp[0][j] = Integer.MAX_VALUE;}for(int i = 0; i <= m; i++) {dp[i][0] = Integer.MAX_VALUE;}dp[0][1] = dp[1][0] = 0;for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++) {dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j-1];}}return dp[m][n];}
}
🌴地下城游戏
🚩题目描述
恶魔们抓住了公主并将她关在了地下城 dungeon 的 右下角 。地下城是由 m x n 个房间组成的二维网格。我们英勇的骑士最初被安置在 左上角 的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快解救公主,骑士决定每次只 向右 或 向下 移动一步。
返回确保骑士能够拯救到公主所需的最低初始健康点数。
注意:任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
-
示例 1:
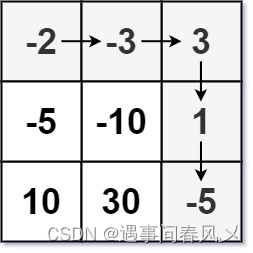
输入:dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
输出:7
解释:如果骑士遵循最佳路径:右 -> 右 -> 下 -> 下 ,则骑士的初始健康点数至少为 7 。 -
示例 2:
输入:dungeon = [[0]]
输出:1
class Solution {public int calculateMinimumHP(int[][] dungeon) {}
}
🚩算法思路
- 状态表⽰:
这道题如果我们定义成:从起点开始,到达 [i, j] 位置的时候,所需的最低初始健康点数。那么我们分析状态转移的时候会有⼀个问题:那就是我们当前的健康点数还会受到后⾯的路径的影响。也就是从上往下的状态转移不能很好地解决问题。
这个时候我们要换⼀种状态表⽰:从 [i, j] 位置出发,到达终点时所需要的最低初始健康点数。这样我们在分析状态转移的时候,后续的最佳状态就已经知晓。
综上所述,定义状态表⽰为:
dp[i][j] 表⽰:从 [i, j] 位置出发,到达终点时所需的最低初始健康点数。
- 状态转移⽅程:
对于 dp[i][j] ,从 [i, j] 位置出发,下⼀步会有两种选择(为了⽅便理解,设 dp[i] [j] 的最终答案是 x ):- ⾛到右边,然后⾛向终点
那么我们在 [i, j] 位置的最低健康点数加上这⼀个位置的消耗,应该要⼤于等于右边位置的最低健康点数,也就是: x + dungeon[i][j] >= dp[i][j + 1] 。通过移项可得: x >= dp[i][j + 1] - dungeon[i][j] 。因为我们要的是最⼩值,因此这种情况下的 x = dp[i][j + 1] - dungeon[i][j] ; - ⾛到下边,然后⾛向终点
那么我们在 [i, j] 位置的最低健康点数加上这⼀个位置的消耗,应该要⼤于等于下边位置的最低健康点数,也就是: x + dungeon[i][j] >= dp[i + 1][j] 。通过移项可得: x >= dp[i + 1][j] - dungeon[i][j] 。因为我们要的是最⼩值,因此这种情况下的 x = dp[i + 1][j] - dungeon[i][j] ;
- ⾛到右边,然后⾛向终点
综上所述,我们需要的是两种情况下的最⼩值,因此可得状态转移⽅程为:dp[i][j] = min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j]
但是,如果当前位置的 dungeon[i][j] 是⼀个⽐较⼤的正数的话, dp[i][j] 的值可能变成 0 或者负数。也就是最低点数会⼩于 1 ,那么骑⼠就会死亡。因此我们求出来的 dp[i][j] 如果⼩于等于 0 的话,说明此时的最低初始值应该为 1 。处理这种情况仅需让 dp[i][j] 与 1 取⼀个最⼤值即可:dp[i][j] = max(1, dp[i][j])
- 初始化:
可以在最前⾯加上⼀个「辅助结点」,帮助我们初始化。使⽤这种技巧要注意两个点:- 辅助结点⾥⾯的值要「保证后续填表是正确的」;
- 「下标的映射关系」。
在本题中,在 dp 表最后⾯添加⼀⾏,并且添加⼀列后,所有的值都先初始化为⽆穷⼤,然后让dp[m][n - 1] = dp[m - 1][n] = 1 即可。
-
填表顺序:
根据「状态转移⽅程」,我们需要「从下往上填每⼀⾏」,「每⼀⾏从右往左」。 -
返回值:
根据「状态表⽰」,我们需要返回 dp[0][0] 的值
🚩代码实现
class Solution {public int calculateMinimumHP(int[][] d) {// 1. 创建 dp 表// 2. 初始化// 3. 填表// 4. 返回值int m = d.length;int n = d[0].length;int[][] dp = new int[m + 1][n + 1];for(int j = 0; j <= n; j++) {dp[m][j] = Integer.MAX_VALUE;}for(int i = 0; i <= m; i++) {dp[i][n] = Integer.MAX_VALUE;}dp[m][n - 1] = dp[m - 1][n] = 1;for(int i = m - 1; i >= 0; i--) {for(int j = n - 1; j >= 0; j--) {dp[i][j] = Math.min(dp[i][j + 1], dp[i + 1][j]) - d[i][j];dp[i][j] = Math.max(dp[i][j], 1);}}return dp[0][0];}
}
⭕总结
关于《【算法优选】 动态规划之路径问题——贰》就讲解到这儿,感谢大家的支持,欢迎各位留言交流以及批评指正,如果文章对您有帮助或者觉得作者写的还不错可以点一下关注,点赞,收藏支持一下!
相关文章:

【算法优选】 动态规划之路径问题——贰
文章目录 🎋前言🌲[下降最小路径和](https://leetcode.cn/problems/minimum-path-sum/)🚩题目描述🚩算法思路:🚩代码实现 🎍[最小路径和](https://leetcode.cn/problems/minimum-path-sum/)&…...

从视频中截取指定帧图片
前言: 我们在很多时候需要对视频文件进行分析,或者对视频产生缩略图。因此视频截取技术必不可少。 从本地文件中读取视频帧 导包 <dependency><groupId>org.jcodec</groupId><artifactId>jcodec</artifactId><versio…...
全套教程2023年12月最新)
2023最新vue安装(npm,yarn,国内镜像,vue安装,vue导包)全套教程2023年12月最新
第一步(安装npm) 官网地址:https://nodejs.org/en/download windows安装yarn 详细教程_windows yarn-CSDN博客 第二步(yarn下载) windows 下需要下载msi文件 ,下载地址:https://yarnpkg.com/latest.msi npm install -g…...
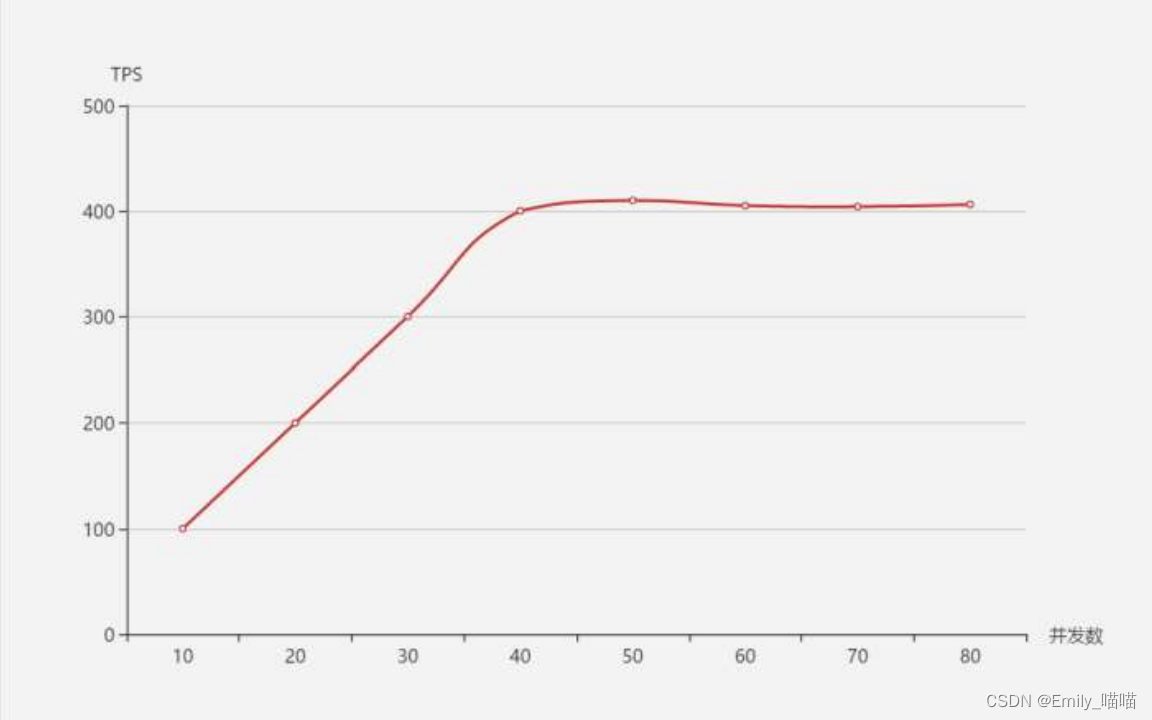
性能测试基础
性能测试分类 客户端性能:测试APP自身的性能,例如CPU、内存消耗;web页面元素渲染速度 服务端性能:测试服务端项目程序的支持的并发、处理能力、响应时间等,主要通过接口来做性能测试 性能测试指标 并发 同时向服务…...

算法与数据结构--最短路径Dijkstra算法
题目: 算法与数据结构实验题 10.20 迷路 ★实验任务 学长经常迷路,现在他又遇到问题了,需要求救。 假设他有一张地图,上面有N个点,M条路,他现在在编号为S的地方,想要去编号为E的地方&#x…...

ASP.NET Core 8 在 Windows 上各种部署模型的性能测试
ASP.NET Core 8 在 Windows 上各种部署模型的性能测试 我们知道 Asp.net Core 在 windows 服务器上部署的方案有 4 种之多。这些部署方案对性能的影响一直以来都是靠经验。比如如果是部署在 IIS 下,那么 In Process 会比 Out Process 快;如果是 Self Hos…...

跨框架解决方案-Mitosis【Context】
Context Mitosis的context必须是: 在自己的文件中创建文件名必须以context.lite.ts结尾默认导出必须是一个返回context对象的函数 // simple.context.lite.ts import { createContext } from builder.io/mitosis;export default createContext({foo: bar,get foo…...

有哪些重要的项目是用 Python 开发的?
请访问 https://www.python.org/about/success 查看使用了 Python 的项目列表。 阅览 历次 Python 会议 的日程纪要可以看到许多不同公司和组织所做的贡献。 高水准的 Python 项目包括 Mailman 邮件列表管理器 和 Zope 应用服务器。 多个 Linux 发行版,其中最著名的…...

【计算机网络】应用层电子邮件协议
一、电子邮件系统架构 电子邮件是一个典型的异步通信系统,发送方从UA,也就是邮件客户端,通过应用层SMTP协议,传输层tcp协议,发送给发送方的邮件服务器,比如使用的是163邮箱,163提供的SMTP服务器…...
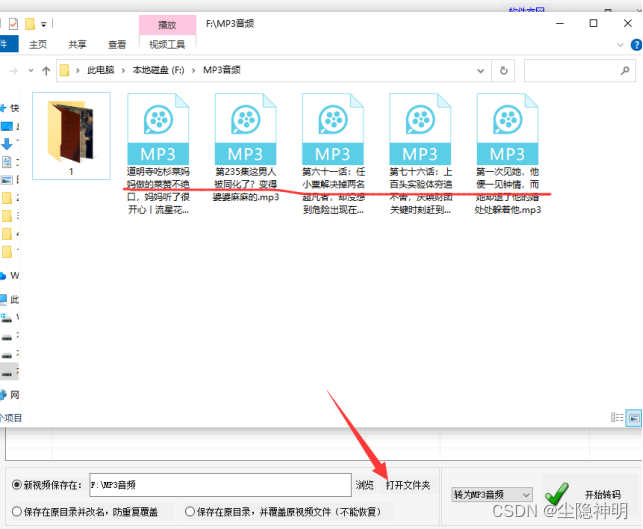
视频剪辑:视频转码实用技巧,批量将MP4转为MP3音频
随着数字媒体设备的普及,视频和音频文件已成为日常生活中的重要组成部分。有时,可能要将MP4视频文件转换为MP3音频文件,以提取其中的音频内容或者进行其他处理。这是耗费时间的任务,那要如何操作呢?本文详解云炫AI智剪…...
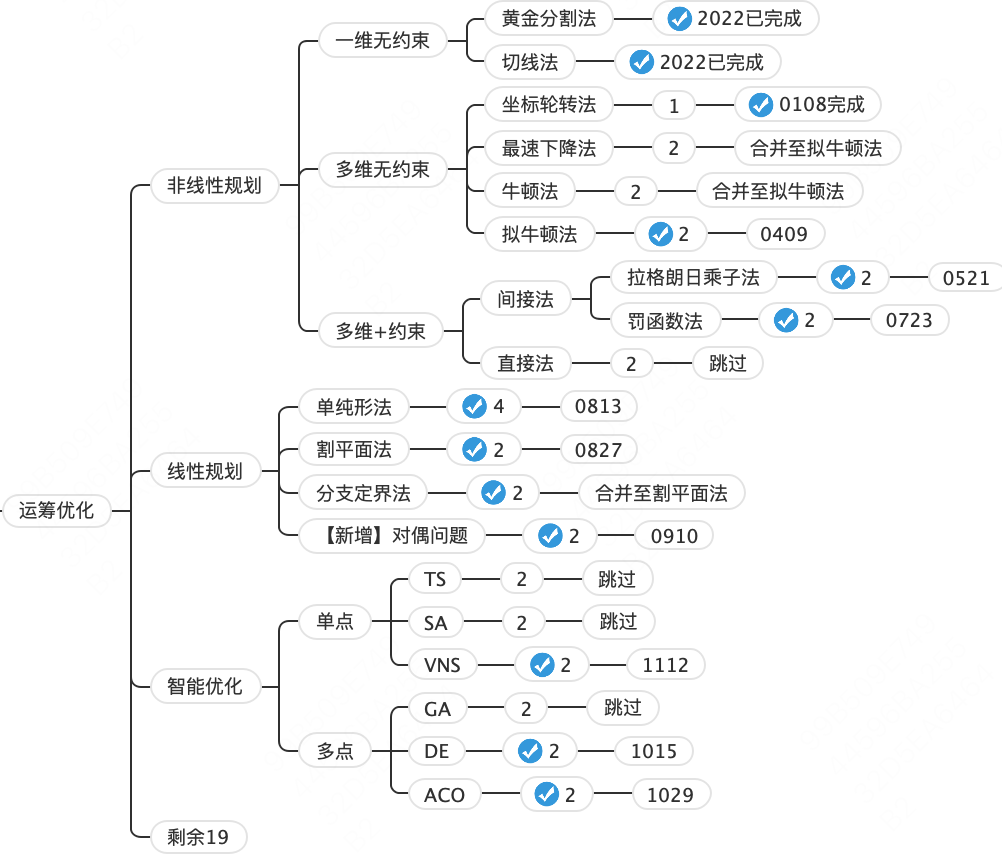
体系化学习运筹学基础算法的实践和总结
文章目录 引言目标设计目标实践文章汇总经验总结一则预告 引言 眨眼间已经12月了,眼看着2023年马上要过完了。 女朋友最近总说,工作以后感觉时间过的好快。事实上,我也是这么认为的。年纪越大,越会担心35岁危机的降临。所以&…...

【Java探索之旅】我与Java的初相识(一):Java的特性与优点及其发展史
🎥 屿小夏 : 个人主页 🔥个人专栏 : Java入门到精通 🌄 莫道桑榆晚,为霞尚满天! 文章目录 一. Java语言概述与优势1.1 Java的概述1.2 Java语言的优势 二. Java领域与发展史2.1 Java的使用领域2.…...

重写 AppiumService 类,添加默认启动参数,并实时显示启动日志
一、前置说明 在Appium的1.6.0版本中引入了AppiumService类,可以很方便的通过该类来管理Appium服务器的启动和停止。经过测试,使用该类的实例执行关闭server时,并没有释放端口号,会导致第二次启动时失败。另外,使用该…...

[方法论]allocation 空间内容分配
区分度 typeanalysisrecognitionconclusion type - 阅读 - 理解- 背诵- 听课 看 听 思考- reproduce/ 默写/ 应用- 背- 想- 写analysis 理解 和 背 是不占用现实空间的,可以在脑内不断消化,可以飞配给没有空间的时间块。 阅读 和 写是占用现实空间的…...

家电制造数字孪生5G智能工厂可视化系统,加速家电制造产业数字化转型
5G数字孪生、三维可视化与工业互联网的融合加速中国新型工业化进程,助推我国从制造大国迈进制造强国。家电行业是中国最具国际竞争力的产业之一,在企业数字化转型中,要求企业从生产设备到数字化系统,一系列的数字化、智能化改革已…...
)
Flink入门之部署(二)
三种部署模式 standalone集群,会话模式部署:先启动flink集群 web UI提交shell命令提交:bin/flink run -d -m hadoop102:8081 -c com.atguigu.flink.deployment.Flinke1_NordCount./Flink-1.0-SNAPSHOT.jar --hostname hadoop102 --port 8888 …...

SQL命令---修改字段名
介绍 使用sql语句修改字段名。 命令 alter table 表名 change 旧字段名 新字段名 新数据类型;例子 将a表id字段名改为id1 alter table a change id id1 int(12) NOT NULL;...

设计模式篇---代理模式
文章目录 概念结构实例静态代理动态代理 总结 概念 代理模式:给某一个对象提供一个代理或占位符,并由代理对象来控制对原对象的访问。 比如我们想从其他国家买东西,但我们无法直接联系外国的商家,可以找代理商,让他们…...

STM32单片机项目实例:基于TouchGFX的智能手表设计(2)UI交互逻辑的设计
STM32单片机项目实例:基于TouchGFX的智能手表设计(2)UI交互逻辑的设计 目录 一、UI交互逻辑的设计 1.1 硬件平台的资源 1.2 界面切换功能 1.3 表盘界面 1.4 运动界面 1.6 设置界面 1.7 应…...
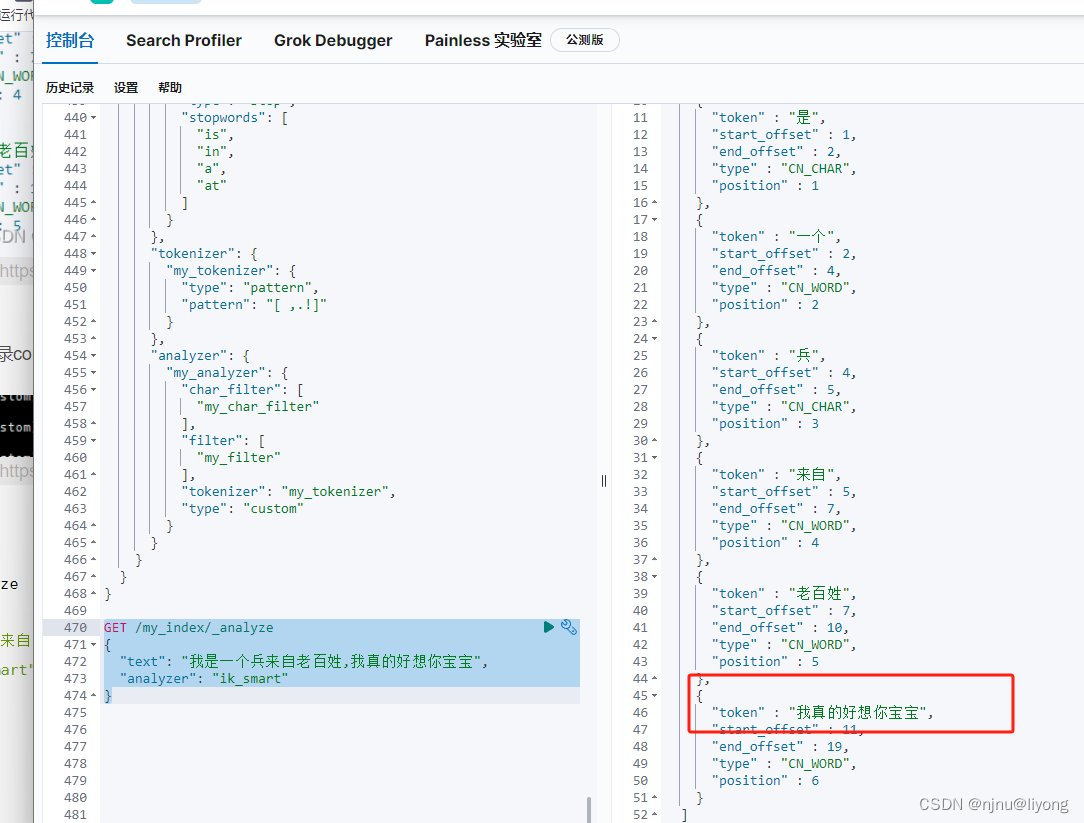
ES-分析器
分析器 两种常用的英语分析器 1 测试工具 #可以通过这个来测试分析器 实际生产环境中我们肯定是配置在索引中来工作 GET _analyze {"text": "My Moms Son is an excellent teacher","analyzer": "english" }2 实际效果 比如我们有下…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...
