排序算法——归并排序
归并排序(Merge Sort)是计算机科学中非常重要的排序算法之一。它不仅高效、稳定,而且是许多高级排序技术和算法思想的基础。在本文中,我们将深入探讨归并排序的原理、实现方法,以及它的优缺点。
1. 归并排序的原理
归并排序是基于分治法(Divide and Conquer)的排序算法。这种方法将大问题分解成小问题,解决小问题,再将小问题的解决方案组合起来解决大问题。
具体来说,归并排序将待排序的数组分成两部分,递归地对这两部分分别进行排序,然后将两个已排序的部分合并成一个整体。这个过程可以分为两个主要阶段:分割(Divide)和合并(Merge)。
分割
- 初始状态下,数组被视为一组无序的元素。
- 数组被递归地分成两半,直到每个子数组只包含一个元素或为空。
合并
- 逐步将小的子数组合并成大的子数组。
- 在合并过程中,子数组的元素会被排序。
2. 归并排序的实现
归并排序通常通过递归来实现。以下是归并排序的一个典型实现(使用 C++):
#include <vector>
using namespace std;void merge(vector<int>& nums, int left, int mid, int right) {vector<int> temp;int i = left, j = mid;while (i < mid && j < right) {if (nums[i] < nums[j]) {temp.push_back(nums[i++]);} else {temp.push_back(nums[j++]);}}while (i < mid) temp.push_back(nums[i++]);while (j < right) temp.push_back(nums[j++]);for (int k = 0; k < temp.size(); k++) {nums[left + k] = temp[k];}
}void mergeSort(vector<int>& nums, int left, int right) {if (left + 1 >= right) return;int mid = left + (right - left) / 2;mergeSort(nums, left, mid);mergeSort(nums, mid, right);merge(nums, left, mid, right);
}
在这段代码中,mergeSort 函数递归地将数组分为更小的部分,然后 merge 函数负责将这些部分合并成一个有序数组。
3. 归并排序的特点
优点
- 稳定性:归并排序是一种稳定的排序算法,不会改变相同元素的初始相对位置。
- 效率:对于大型数据集,归并排序提供了 O(n log n) 的时间复杂度,这是相当高效的。
缺点
- 空间复杂度:归并排序需要额外的存储空间(O(n)),这可能在内存受限的系统中成为问题。
- 递归:由于它基于递归实现,对于非常大的数据集,可能导致堆栈溢出。
4. 应用场景
归并排序非常适用于大规模数据集的排序,特别是在外部排序中表现出色,例如,当数据太大而不能全部加载到内存中时。由于其稳定性,归并排序也被广泛应用于那些需要维持元素原有顺序的场景中。
相关文章:

排序算法——归并排序
归并排序(Merge Sort)是计算机科学中非常重要的排序算法之一。它不仅高效、稳定,而且是许多高级排序技术和算法思想的基础。在本文中,我们将深入探讨归并排序的原理、实现方法,以及它的优缺点。 1. 归并排序的原理 归…...

2023 年安徽省职业院校技能大赛高职组“软件测试”赛项样题
2023 年安徽省职业院校技能大赛 高职组“软件测试”赛项样题 目录 任务一:功能测试(45 分) 1、测试计划(5 分) 2、测试用例(15 分) 3、Bug 清单(20 分) 4、测试报告&…...

Mysql8和Oracle实际项目中递归查询树形结构
背景: 项目升级,引入MySQL数据库,之前一直用的是Oracle数据,在做用户登录单位维护的时候,需要返回该用户所属单位下的所有子单位。下边是模拟项目数据实践的过程。 数据准备: 准备一张单位表,…...
docker mysql8 设置不区分大小写
docker安装Mysql8.0的坑之lower_case_table_names_docker mysql lower_case_table_names-CSDN博客https://blog.csdn.net/p793049488/article/details/108365929 docker run ‐di ‐‐nametensquare_mysql ‐p 33306:3306 ‐e MYSQL_ROOT_PASSWORD123456 mysql...
 代码学习—常见问题3)
Audio Siganl (MATLAB) 代码学习—常见问题3
问题描述 生成信号y1: 8000个样本,1000个周期,幅度为0.85的余弦信号。若信号的持续时间为1s,则采样频率和信号频率为多少。生成信号y2: 持续时间为1s,幅度为0.7,频率为500Hz,相位为 π / 4 \pi/4 π/4生成信号y:y_1+y_2绘制前200ms的y信号示意图计算y的DFT绘制频域示意图…...

【PTA题目】7-8 矩阵运算 分数 10
7-8 矩阵运算 分数 10 全屏浏览题目 切换布局 作者 C课程组 单位 浙江大学 给定一个nn的方阵,本题要求计算该矩阵除副对角线、最后一列和最后一行以外的所有元素之和。副对角线为从矩阵的右上角至左下角的连线。 输入格式: 输入第一行给出正整数n(…...

Ubuntu20.04创建并挂在zfs池
Ubuntu 下使用 ZFS [适用于中高级用户] 主磁盘上清洁安装带有ZFS的Ubuntu后,可以开始体验其特性。 所有ZFS配置过程都需要命令行。 我不知道有GUI工具。 创建一个 ZFS 池 本节仅适用于具有多个磁盘的系统。 如果只有一个磁盘,Ubuntu会在安装时自动创建…...
)
x的平方根算法(leetcode第69题)
题目描述: 给你一个非负整数 x ,计算并返回 x 的 算术平方根 。由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。…...

打破空间限制,畅享真实生活
直播已经成为了当今社会中非常流行的一种娱乐方式,也是人们获取信息和互动的重要渠道之一。而无绿幕直播,则是近年来兴起的一种特殊形式,它打破了以往直播的空间限制,让观众们能够更贴近主播,更真实地感受到直播背后的…...

Python基础期末复习 新手 2
虽然age 10在__init__方法中定义了一个局部变量age,但这个局部变量并不会影响类属性age的值。类属性是在类级别上定义的,不属于任何一个实例。因此,在创建实例s1和s2时,它们的age属性值都为类属性的初始值0。 尽管对类的属性值进…...

Java接入ChatGPT接口简单示例
我们定义了一个名为ChartGPTConfig的类,它有两个私有成员变量apiKey和apiUrl,分别表示ChartGPT的API密钥和API URL。 public class ChartGPTConfig {private final String apiKey;private final String apiUrl;public ChartGPTConfig(String apiKey, St…...

解决夜神模拟器与Android studio自动断开的问题
原因:夜神模拟器的adb版本和Android sdk的adb版本不一致 解决办法: 1.找到android的sdk (1)File--->Project Structure (2)SDK Location:记下sdk的位置 2.找到sdk中的adb文件 SDK-->platform-tools-->adb.exe 3.复制…...

利用C语言模拟实现堆的基本操作和调堆算法
利用C语言模拟实现堆的基本操作和调堆算法 文章目录 利用C语言模拟实现堆的基本操作和调堆算法前言一、堆的基本原理大根堆和小根堆的比较 二、实现堆的基本操作1)结构定义2)初始化堆(HeapInit)3)销毁堆(He…...

react hooks之useRef和useImperativeHandle
为什么这两个一起写,是因为这两个关联性很大,逐一介绍。 一:useRef 1、作用:用于在函数组件中创建一个持久化的引用变量。这个引用变量可以在组件的多次渲染之间保持不变,并且可以访问和修改 DOM 元素或其他组件实例…...

scala方法与函数
定义方法定义函数方法和函数的区别scala的方法函数操作 1.9 方法与函数 1.9.1 定义方法 定义方法的基本格式是: def 方法名称(参数列表):返回值类型 方法体 def add(x: Int, y: Int): Int x y println(add(1, 2)) // 3 //也…...
前端框架(Front-end Framework)和库(Library)的区别
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...
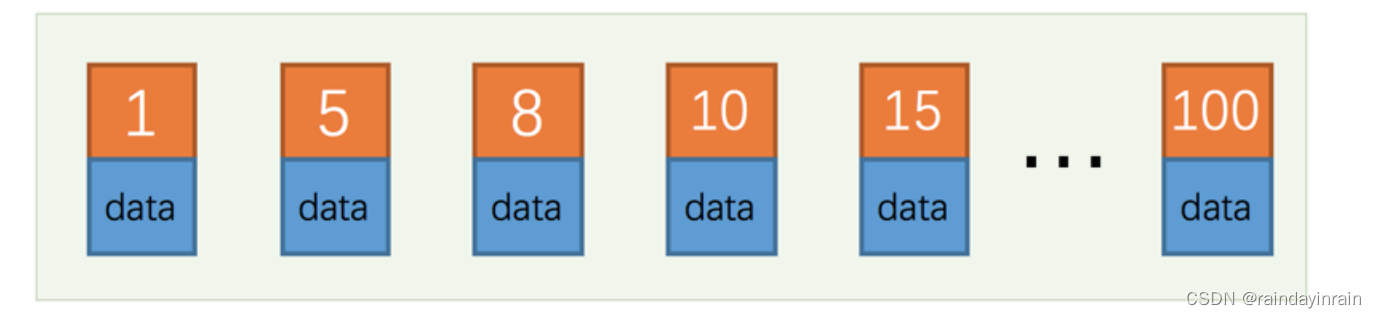
mysql原理--B+树索引的使用
1.索引的代价 在介绍如何更好的使用索引之前先要了解一下使用这玩意儿的代价,它在空间和时间上都会拖后腿: (1). 空间上的代价 这个是显而易见的,每建立一个索引都要为它建立一棵 B 树,每一棵 B 树的每一个节点都是一个数据页&…...

Android : Room 数据库的基本用法 —简单应用_三_版本
在实体类中添加了新字段: Entity(tableName "people") public class People {//新添加的字段private String email;public String getEmail() {return email;}public void setEmail(String email) {this.email email;}} 再次编译启动时会报错…...
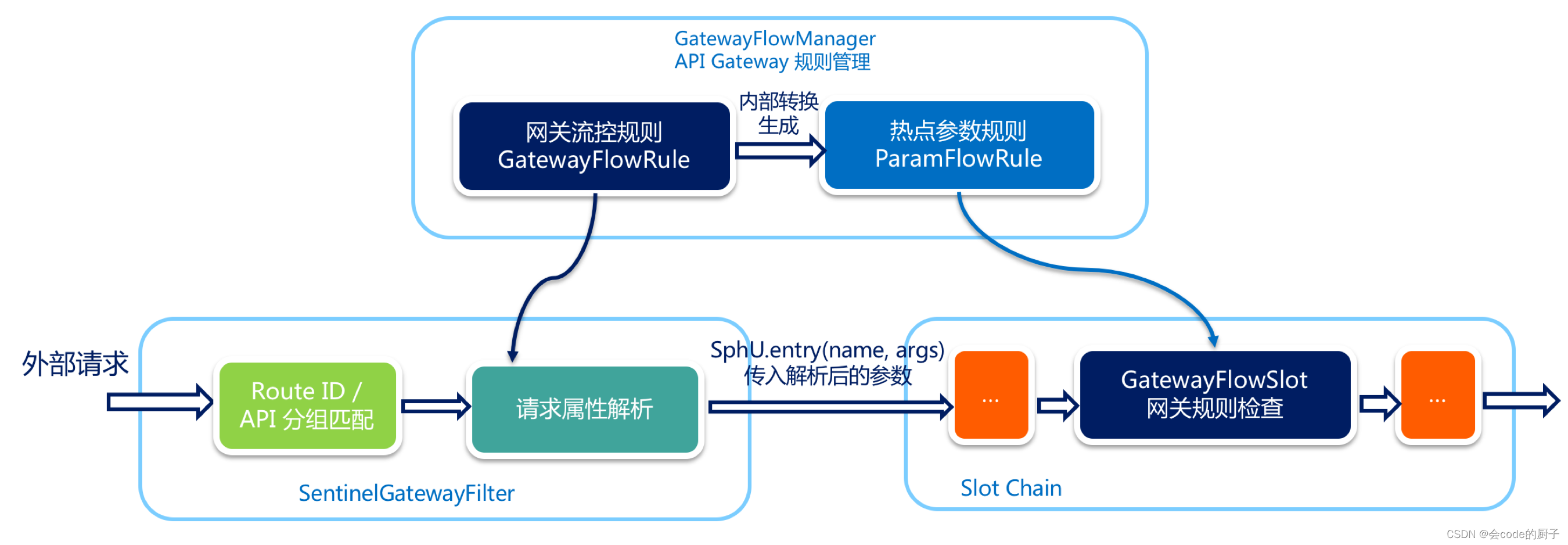
微服务网关组件Gateway实战
1. 需求背景 在微服务架构中,通常一个系统会被拆分为多个微服务,面对这么多微服务客户端应该如何去调用呢?如果根据每个微服务的地址发起调用,存在如下问题: 客户端多次请求不同的微服务,会增加客户端代码…...
)
目标检测YOLO系列从入门到精通技术详解100篇-【目标检测】三维重建(补充篇)
目录 前言 算法原理 三维重建意义 三维重建定义 常见的三维重建表达方式...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...

Pandas 可视化集成:数据科学家的高效绘图指南
为什么选择 Pandas 进行数据可视化? 在数据科学和分析领域,可视化是理解数据、发现模式和传达见解的关键步骤。Python 生态系统提供了多种可视化工具,如 Matplotlib、Seaborn、Plotly 等,但 Pandas 内置的可视化功能因其与数据结…...

mq安装新版-3.13.7的安装
一、下载包,上传到服务器 https://github.com/rabbitmq/rabbitmq-server/releases/download/v3.13.7/rabbitmq-server-generic-unix-3.13.7.tar.xz 二、 erlang直接安装 rpm -ivh erlang-26.2.4-1.el8.x86_64.rpm不需要配置环境变量,直接就安装了。 erl…...
