利用C语言模拟实现堆的基本操作和调堆算法
利用C语言模拟实现堆的基本操作和调堆算法
文章目录
- 利用C语言模拟实现堆的基本操作和调堆算法
- 前言
- 一、堆的基本原理
- 大根堆和小根堆的比较
- 二、实现堆的基本操作
- 1)结构定义
- 2)初始化堆(HeapInit)
- 3)销毁堆(HeapDestroy)
- 4)堆的调整算法
- (1)向上调堆算法
- (2)向下调堆算法
- 5)堆的插入操作(HeapPush)
- 6)堆的删除操作(HeapPop)
- 7)获取堆顶元素(HeapTop)
- 8)获取堆的大小(HeapSize)
- 9)判断堆是否为空(HeapEmpty)
- 10)打印堆(HeapPrint)
- 三、测试堆的功能
- 总结
前言
堆是一种重要而高效的数据结构,广泛应用于各种算法和数据处理场景。本篇博客将介绍如何使用C语言模拟实现堆的基本操作,包括初始化、插入、删除等,并通过回调函数和函数指针的灵活运用,实现大根堆和小根堆的不同调堆算法。
一、堆的基本原理
堆是一种特殊的树形数据结构,具有以下基本特点:
- 完全二叉树的结构,即除了最底层,其他层都是满的。
- 堆中的每个节点的值都必须大于等于或小于等于其子节点的值,根据此条件分为大根堆和小根堆。
堆常被用来实现优先队列等数据结构,其中最值的快速访问是堆的主要优势。
大根堆和小根堆的比较
大根堆和小根堆的不同之处在于调堆算法中的比较条件。在大根堆中,父节点的值必须大于子节点的值;而在小根堆中,父节点的值必须小于子节点的值。通过函数指针,我们可以根据用户的选择动态切换调堆算法,使代码更加灵活。
二、实现堆的基本操作
声明: 此处采用动态数组模拟实现堆(完全二叉树)
1)结构定义
定义了堆的结构,包括元素数组、大小、容量和标识是大根堆还是小根堆的字符。
typedef int HPDataType;typedef struct Heap {HPDataType* a;size_t size;size_t capacity;char RootBigOrSmall;
} HP;
2)初始化堆(HeapInit)
通过 HeapInit 函数初始化堆结构,用户可以选择大根堆(‘B’或’b’)或小根堆(‘S’或’s’)。
void HeapInit(HP* php)
{assert(php);printf("请挑选大根堆(big -> B)或小根堆(small -> S): 【输入首字母大小写】");char choose = ' ';choose = getchar();if (choose == 'B' || choose == 'S' || choose == 'b' || choose == 's') { php->RootBigOrSmall = choose; }else { printf("输入有误!"); return; }php->a = NULL;php->capacity = php->size = 0;
}
3)销毁堆(HeapDestroy)
释放堆内存和相关资源的 HeapDestroy 函数。
void HeapDestroy(HP* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}
4)堆的调整算法
(1)向上调堆算法
void adjustUpHeap(HPDataType* a, size_t child, bool (*cmp)(HPDataType _parent, HPDataType _child))
{size_t parent = (child - 1) / 2;if (child == 0) { parent = 0; }while (child > 0){if (cmp(a[parent], a[child])){HPDataType tmp = a[parent];a[parent] = a[child];a[child] = tmp;}child = parent;parent = (parent - 1) / 2;}
}
(2)向下调堆算法
void adjustDownHeap(HPDataType* a, HPDataType size, HPDataType parent,bool (*cmp)(HPDataType _parent, HPDataType _child))
{HPDataType child = parent * 2 + 1;while (child < size){if (child + 1 < size && cmp(a[child], a[child + 1])){child++;}if (cmp(a[parent], a[child])){HPDataType tmp = a[parent];a[parent] = a[child];a[child] = tmp;parent = child;child = child * 2 + 1;}else { break; }}
}
这里采用函数指针作为两种调堆算法的参数是因为通过此方法可实现运行后指定大根堆或小根堆从而影响相关控制堆的操作,比如 HeapPush和 HeapPop等操作。
5)堆的插入操作(HeapPush)
通过 HeapPush 函数插入元素,并通过向上调堆算法保持堆的性质。
void HeapPush(HP* php, HPDataType x)
{assert(php);// 检查扩容if (php->capacity == php->size){size_t new_capacity = (php->capacity == 0 ? 4 : php->capacity * 2);HPDataType* tmp = (HPDataType*)realloc(php->a, new_capacity * sizeof(HPDataType));if (!tmp) { perror("realloc of HeapPush"); return; }php->a = tmp;php->capacity = new_capacity;}php->a[php->size++] = x;// 调堆bool (*cmp)(HPDataType _parent, HPDataType _child) = NULL;if (php->RootBigOrSmall == 'B' || php->RootBigOrSmall == 'b'){cmp = bigRootHeap_cmp;}else{cmp = smallRootHeap_cmp;}adjustUpHeap(php->a, php->size - 1, cmp);
}
注意: 这里使用动态数组存储堆的节点,所以需要考虑空间扩容问题,当容量不足时利用 realloc() 函数从堆区申请额外空间。
6)堆的删除操作(HeapPop)
通过 HeapPop 函数删除堆顶元素,并通过调堆算法保持堆的性质。
void HeapPop(HP* php)
{assert(php);assert(php->a && php->size > 0);bool (*cmp)(HPDataType _parent, HPDataType _child) = NULL;if (php->RootBigOrSmall == 'B' || php->RootBigOrSmall == 'b'){cmp = bigRootHeap_cmp;}else{cmp = smallRootHeap_cmp;}// 去顶节点HPDataType tmp = php->a[0];php->a[0] = php->a[php->size - 1];php->a[php->size - 1] = tmp;php->size--;// 调堆adjustDownHeap(php->a, php->size, 0, cmp);
}
7)获取堆顶元素(HeapTop)
通过 HeapTop 函数获取堆顶元素。
HPDataType HeapTop(const HP* php)
{assert(php);assert(php->a && php->size > 0);return php->a[0];
}
8)获取堆的大小(HeapSize)
通过 HeapSize 函数获取堆的大小。
size_t HeapSize(const HP* php)
{assert(php);return php->size;
}
9)判断堆是否为空(HeapEmpty)
通过 HeapEmpty 函数判断堆是否为空。
bool HeapEmpty(const HP* php)
{assert(php);return php->size == 0;
}
10)打印堆(HeapPrint)
通过 HeapPrint 函数输出堆的内容。(测试时避免代码冗杂)
void HeapPrint(const HP* php)
{assert(php);for (int i = 0; i < php->size; i++){std::cout << php->a[i] << '\t';}std::cout << "\n";
}
三、测试堆的功能
测试代码:
int main()
{HP hp;HeapInit(&hp);HeapPush(&hp, 15);HeapPush(&hp, 18);HeapPush(&hp, 19);HeapPush(&hp, 25);HeapPush(&hp, 28);HeapPush(&hp, 34);HeapPush(&hp, 65);HeapPush(&hp, 49);HeapPush(&hp, 27);HeapPush(&hp, 37);HeapPrint(&hp);HeapPush(&hp, 30);HeapPrint(&hp);HeapPop(&hp);HeapPrint(&hp);HeapDestroy(&hp);return 0;
}
通过 HeapPrint可以将上面代码分为三部分,第一次 HeapPrint时,对应数组内元素为:

树状图:

第二次HeapPrint时:
经历了HeapPush功能,对应数组内元素为:

树状图:

第三次HeapPrint时:
经历HeapPop功能:(向下调整算法)

所得对应数组内元素为:

运行结果:

无内存泄漏,HeapDestroy符合设计需求。
总结
本文详细介绍了使用C语言模拟实现堆的基本操作和调堆算法。通过回调函数和函数指针,实现了大根堆和小根堆的灵活切换。堆是一种强大的数据结构,能够在很多应用中提供高效的解决方案。在实际编程中,理解和掌握堆的实现原理对于优化算法和提高代码效率至关重要。

相关文章:

利用C语言模拟实现堆的基本操作和调堆算法
利用C语言模拟实现堆的基本操作和调堆算法 文章目录 利用C语言模拟实现堆的基本操作和调堆算法前言一、堆的基本原理大根堆和小根堆的比较 二、实现堆的基本操作1)结构定义2)初始化堆(HeapInit)3)销毁堆(He…...

react hooks之useRef和useImperativeHandle
为什么这两个一起写,是因为这两个关联性很大,逐一介绍。 一:useRef 1、作用:用于在函数组件中创建一个持久化的引用变量。这个引用变量可以在组件的多次渲染之间保持不变,并且可以访问和修改 DOM 元素或其他组件实例…...

scala方法与函数
定义方法定义函数方法和函数的区别scala的方法函数操作 1.9 方法与函数 1.9.1 定义方法 定义方法的基本格式是: def 方法名称(参数列表):返回值类型 方法体 def add(x: Int, y: Int): Int x y println(add(1, 2)) // 3 //也…...
前端框架(Front-end Framework)和库(Library)的区别
聚沙成塔每天进步一点点 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 欢迎来到前端入门之旅!感兴趣的可以订阅本专栏哦!这个专栏是为那些对Web开发感兴趣、刚刚踏入前端领域的朋友们量身打造的。无论你是完全的新手还是有一些基础的开发…...
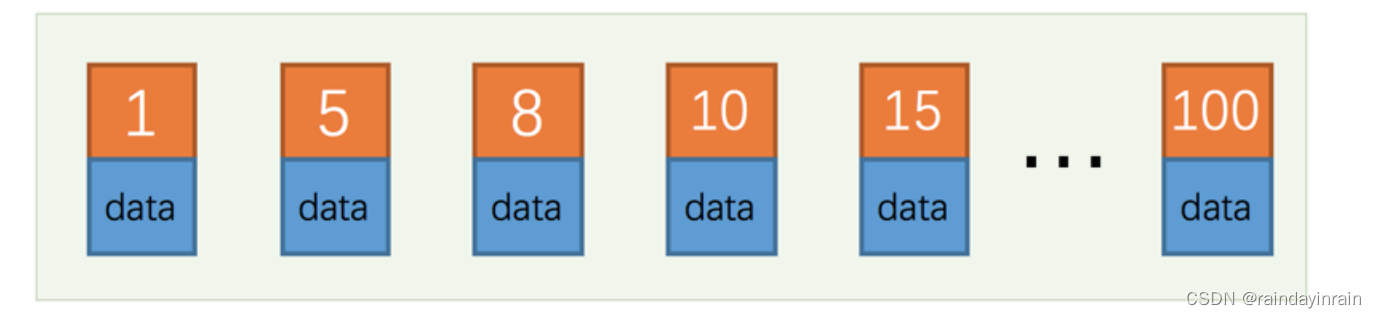
mysql原理--B+树索引的使用
1.索引的代价 在介绍如何更好的使用索引之前先要了解一下使用这玩意儿的代价,它在空间和时间上都会拖后腿: (1). 空间上的代价 这个是显而易见的,每建立一个索引都要为它建立一棵 B 树,每一棵 B 树的每一个节点都是一个数据页&…...

Android : Room 数据库的基本用法 —简单应用_三_版本
在实体类中添加了新字段: Entity(tableName "people") public class People {//新添加的字段private String email;public String getEmail() {return email;}public void setEmail(String email) {this.email email;}} 再次编译启动时会报错…...
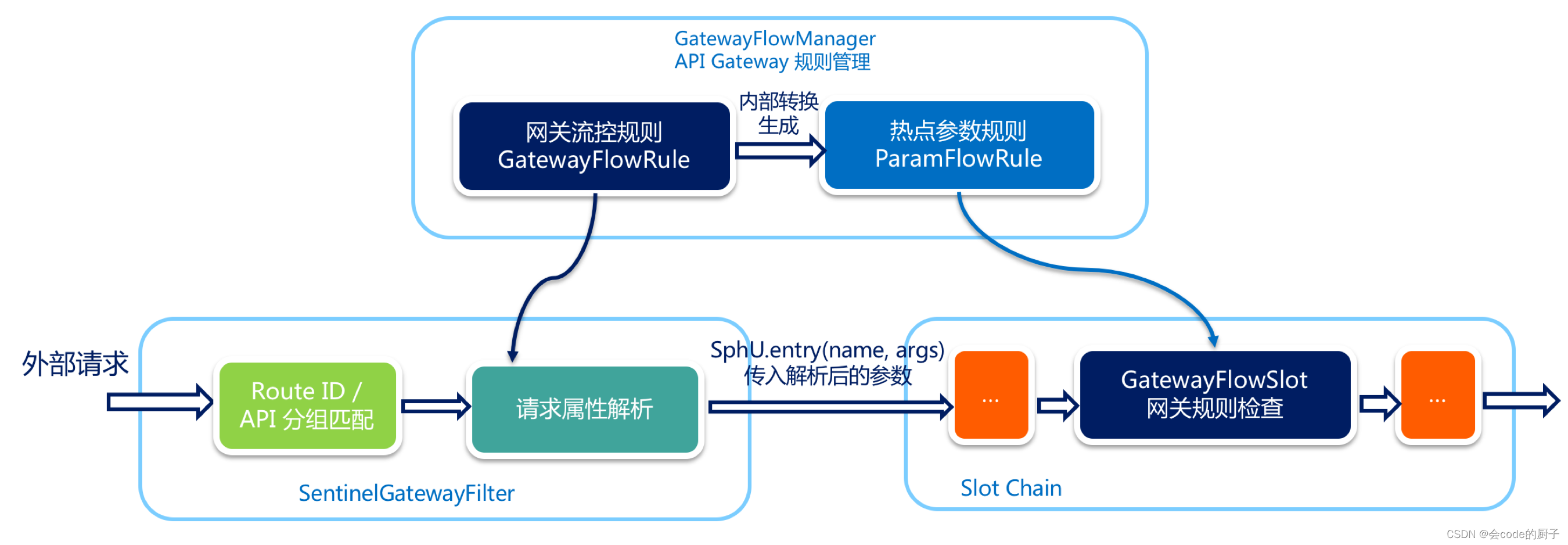
微服务网关组件Gateway实战
1. 需求背景 在微服务架构中,通常一个系统会被拆分为多个微服务,面对这么多微服务客户端应该如何去调用呢?如果根据每个微服务的地址发起调用,存在如下问题: 客户端多次请求不同的微服务,会增加客户端代码…...
)
目标检测YOLO系列从入门到精通技术详解100篇-【目标检测】三维重建(补充篇)
目录 前言 算法原理 三维重建意义 三维重建定义 常见的三维重建表达方式...

关于uniapp X 的最新消息
uni-app x 是什么? uni-app x,是下一代 uni-app,是一个跨平台应用开发引擎。 uni-app x 没有使用js和webview,它基于 uts 语言。在App端,uts在iOS编译为swift、在Android编译为kotlin,完全达到了原生应用的…...
一定数量的行)
spark从表中采样(随机选取)一定数量的行
在Spark SQL中,你可以使用TABLESAMPLE来按行数对表进行采样。以下是使用TABLESAMPLE的示例: SELECT * FROM table_name TABLESAMPLE (1000 ROWS);在这个示例中,table_name是你要查询的表名。TABLESAMPLE子句后面的(1000 ROWS)表示采样的行数…...
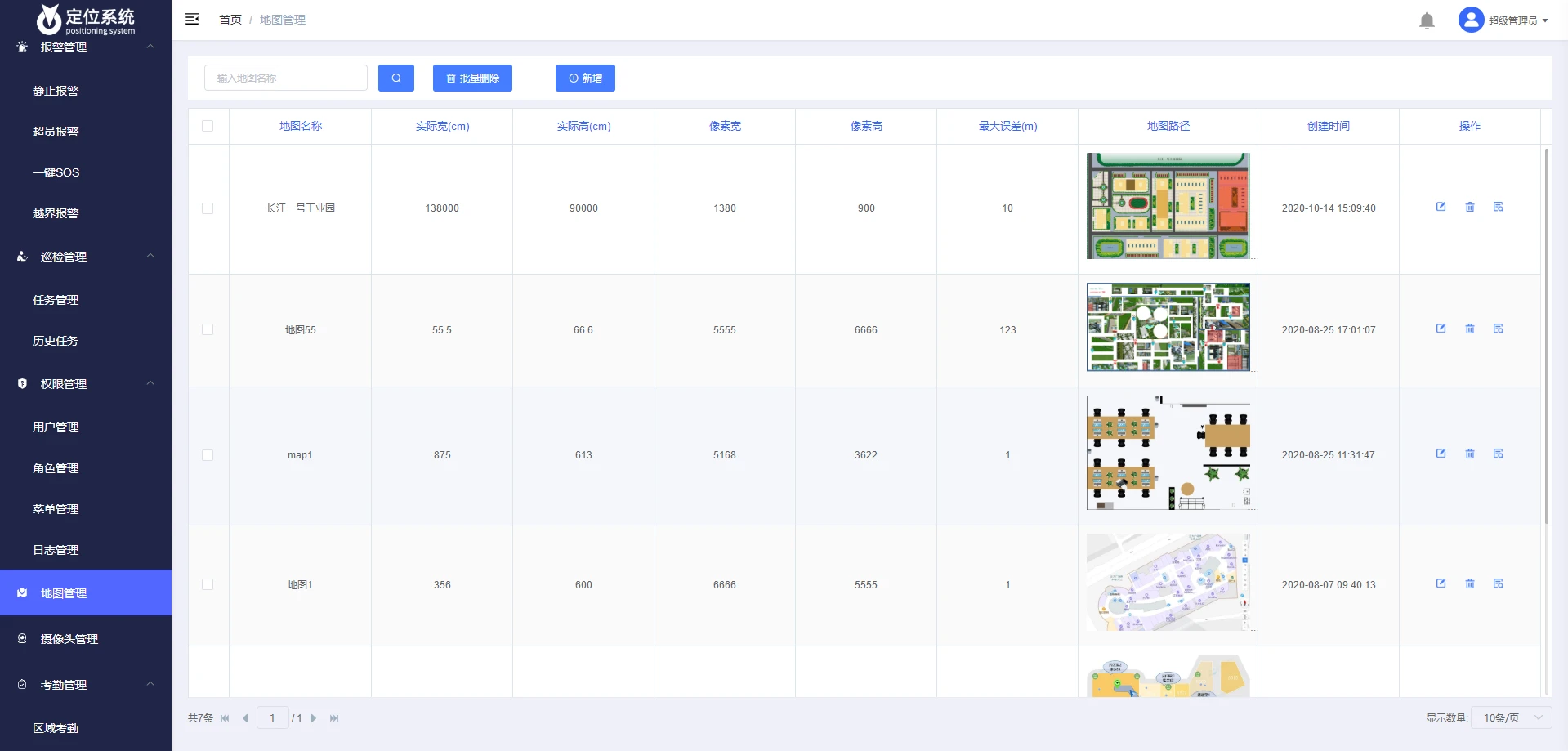
java定位系统源码,UWB技术的无线定位系统源码
UWB技术是一种传输速率高,发射功率较低,穿透能力较强并且是基于极窄脉冲的无线技术。UWB最优的应用环境是室内或者相对密闭的空间,有着厘米级的定位精度,不仅可以非常精准地进行位置跟踪,还可以快速地进行数据传输。 智…...

阿里云sls日志服务如何查某个具体字段的平均数
1: 需求: 查询线上某个接口(如:list_new)的成功率和时延 查接口时延的写法在网上找了一堆,都是语法错误,最后在阿里云官方api找到了正确的 2:贴一下阿里云官方文档: 聚…...

Java八股文面试全套真题【含答案】- Maven篇
以下是一些关于Maven的经典面试题以及它们的答案: 什么是Maven? Maven是一个项目管理工具,用于构建、发布和管理Java项目。它提供了一种标准化的项目结构、依赖管理和构建过程。Maven的核心概念是什么? Maven的核心概念包括POM文…...

从零构建属于自己的GPT系列6:模型本地化部署2(文本生成函数解读、模型本地化部署、文本生成文本网页展示、代码逐行解读)
🚩🚩🚩Hugging Face 实战系列 总目录 有任何问题欢迎在下面留言 本篇文章的代码运行界面均在PyCharm中进行 本篇文章配套的代码资源已经上传 从零构建属于自己的GPT系列1:数据预处理 从零构建属于自己的GPT系列2:模型训…...

不同品牌的手机如何投屏到苹果MacBook?例如小米、华为怎样投屏比较好?
习惯使用apple全家桶的人当然知道苹果手机或iPad可以直接用airplay投屏到MacBook。 但工作和生活的多个场合里,并不是所有人都喜欢用同一品牌的设备,如果同事或同学其他品牌的手机需要投屏到MacBook,有什么方法可以快捷实现? 首先…...

路由和网络周期
### 路由(Routing): 1. **路由的概念:** 路由是用于确定用户在网站或应用程序中所处位置的机制。它可以将不同的 URL 映射到对应的页面或视图组件,使得用户可以通过不同的 URL 访问不同的内容。 2. **路由器…...

【算法与数据结构】332、LeetCode重新安排行程
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:本题比较属于困难题目,难点在于完成机票、出发机场和到达机场之间的映射关系,再…...
)
阶段五:深度学习和人工智能(掌握使用TensorFlow或PyTorch进行深度学习)
掌握使用TensorFlow或PyTorch进行深度学习需要具备一定的编程基础和数学基础,包括编程语言、数据结构、算法、线性代数、概率论和统计学等方面的知识。以下是掌握使用TensorFlow或PyTorch进行深度学习的一些基本要求: 了解深度学习的基本概念和原理&…...
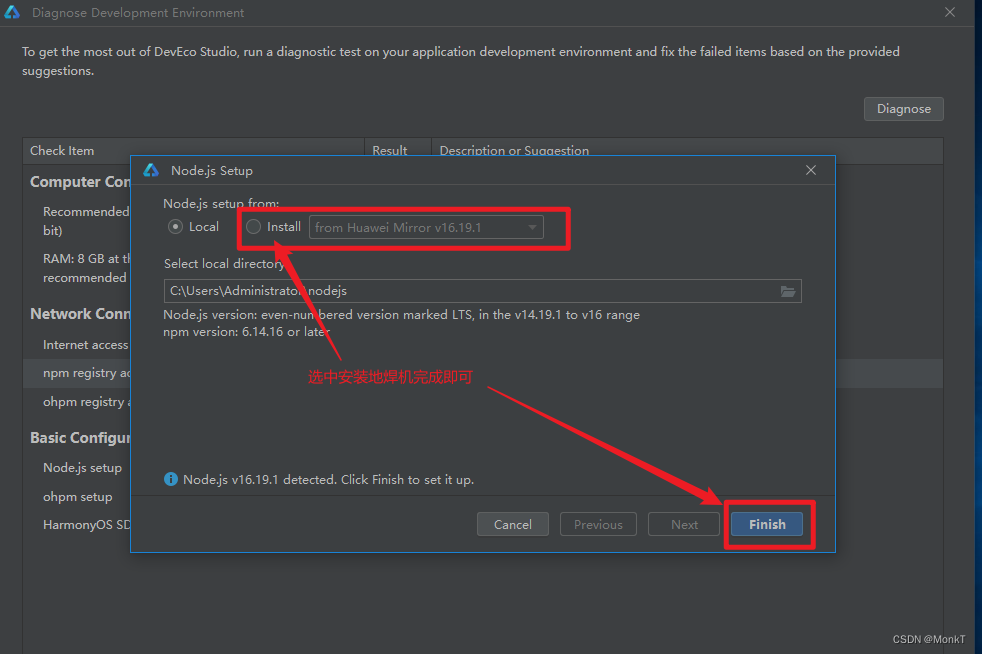
DevEco Studio IDE 创建项目时候配置环境
DevEco Studio IDE 创建项目时候配置环境 一、安装环境 操作系统: Windows 10 专业版 IDE:DevEco Studio 3.1 SDK:HarmonyOS 3.1 二、在配置向导的时候意外关闭配置界面该如何二次配置IDE环境。 打开IDE的界面是这样的。 点击Create Project进行环境配置。 点击OK后出现如…...

HTML面试题---专题二
文章目录 一、前言二、解释input标签中占位符属性的用途三、如何在 HTML 中设置复选框或单选按钮的默认选中状态?四、表单输入字段中必填属性的用途是什么?五、如何使用 HTML 创建表格?六、解释a标签中目标属性的用途七、如何创建一个点击后会…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

高防服务器价格高原因分析
高防服务器的价格较高,主要是由于其特殊的防御机制、硬件配置、运营维护等多方面的综合成本。以下从技术、资源和服务三个维度详细解析高防服务器昂贵的原因: 一、硬件与技术投入 大带宽需求 DDoS攻击通过占用大量带宽资源瘫痪目标服务器,因此…...

数据库——redis
一、Redis 介绍 1. 概述 Redis(Remote Dictionary Server)是一个开源的、高性能的内存键值数据库系统,具有以下核心特点: 内存存储架构:数据主要存储在内存中,提供微秒级的读写响应 多数据结构支持&…...
