动态规划学习——通符串匹配,正则表达式
目录
编辑
一,通符串匹配
1.题目
2.题目接口
3,解题思路及其代码
二,正则表达
1.题目
2.题目接口
3.解题思路及其代码
三,交错字符串
1.题目
2,题目接口
3.解题思路及其代码
一,通符串匹配
1.题目
给你一个输入字符串 (
s) 和一个字符模式 (p) ,请你实现一个支持'?'和'*'匹配规则的通配符匹配:
'?'可以匹配任何单个字符。'*'可以匹配任意字符序列(包括空字符序列)。判定匹配成功的充要条件是:字符模式必须能够 完全匹配 输入字符串(而不是部分匹配)。
示例 1:
输入:s = "aa", p = "a" 输出:false 解释:"a" 无法匹配 "aa" 整个字符串。示例 2:
输入:s = "aa", p = "*" 输出:true 解释:'*' 可以匹配任意字符串。示例 3:
输入:s = "cb", p = "?a" 输出:false 解释:'?' 可以匹配 'c', 但第二个 'a' 无法匹配 'b'。提示:
0 <= s.length, p.length <= 2000s仅由小写英文字母组成p仅由小写英文字母、'?'或'*'组成
2.题目接口
class Solution {
public:bool isMatch(string s, string p) {}
};3,解题思路及其代码
在做动态规划问题时一般都是按照以下几步来走的:
1.确定状态转移方程
像这种两个字符串的问题,一般都是定义二维的dp表按照两个字符串的第i和j下标位置来解决问题的。所以在这里定义dp[i][j]表示p在区间[1,j]中的字符是否存在能够匹配s在[1,i]中的字符。
2.状态转移方程
以s的第i个位置,p的第j个位置为研究对象来研究问题。此时分三种情况:1.s[i] == p[j],或者p[j] == '?',在这种情况下dp[i][j] = dp[i-1][j-1]。
2.p[j] == "*",在这种情况下就要看这个*可以顶替掉多少个s中的字符了:
顶替0个:dp[i][j] = dp[i][j-1]
顶替1个:dp[i][j] = dp[i-1][j-1]
顶替2个:dp[i][j] = dp[i-2][j-1]
顶替3个:dp[i][j] = dp[i-3][j-1]......
在以上i种情况下,我们只要找到一个为真便可以了。所以dp[i][j] = dp[i][j-1]||dp[i-1][j-1]||dp[i-2][j-1]||dp[i-3][j-1].....。但是这样表示的话就需要遍历一遍,所以我们必须要优化以上状态表达,优化成为dp[i][j] = dp[i][j-1]||dp[i-1][j]。通过数学推导得知(将dp[i][j-1]后面的表达式转为一个状态表示)。
3.s[i]!=p[j]并且不是以上情况,在这种条件下dp[i][j]直接就是false。
3.初始化:
1.在字符串问题里,我们一般会在字符串的开头加上一个' '。
2.因为*是可以匹配空的,所以当s字符串为空串时p为空串或者p全为*时也是可以匹配的。
初始化如下:
s = ' '+s; p = ' '+p;dp[0][0] = true; //初始化:当我的s是一个空串时,我的p都是* for(int i = 1;i<n+1;i++) if(dp[0][i-1]&&p[i] == '*') dp[0][i] = true;4.填表顺序
根据状态转移方程很容易得出dp表的填写顺序是从左到右,从上到下。
5.返回值
根据状态表示可知返回值是dp[m][n](m表示s的长度,n表示p的长度)
代码:
class Solution { public:bool isMatch(string s, string p) {int m = s.size();int n = p.size();vector<vector<bool>>dp(m+1,vector<bool>(n+1));//dp[i][j]表示s,p分别以i,j结尾能不能完全匹配s = ' '+s;p = ' '+p;dp[0][0] = true;//初始化:当我的s是一个空串时,我的p都是*for(int i = 1;i<n+1;i++) if(dp[0][i-1]&&p[i] == '*') dp[0][i] = true;//以i,j为结尾研究问题for(int i = 1;i<m+1;i++){for(int j = 1;j<n+1;j++){//分两种情况if(p[j] == s[i]||p[j] == '?'){dp[i][j] = dp[i-1][j-1];}else if(p[j] == '*'){//这颗*可以若干个字符,那可以配0个或者无数个得到的状态转移方程如下//如果不匹配dp[i][j] = dp[i][j-1]//如果匹配1个dp[i][j] = dp[i-1][j-1]//如果匹配两个dp[i][j] = dp[i-2][j-1]//.......//在上面的情况中我们只要找到一种便可以//dp[i][j] = dp[i][j-1]||dp[i-1][j-1]||dp[i-2][j-1]||dp[i-3][j-1]......//优化:将上面的i个表达式变成n个表达式表示:dp[i][j] = dp[i][j-1]||dp[i-1][j] dp[i][j] = dp[i-1][j]||dp[i][j-1];}}} return dp[m][n];} };
二,正则表达
1.题目
给你一个字符串
s和一个字符规律p,请你来实现一个支持'.'和'*'的正则表达式匹配。
'.'匹配任意单个字符'*'匹配零个或多个前面的那一个元素所谓匹配,是要涵盖 整个 字符串
s的,而不是部分字符串。示例 1:
输入:s = "aa", p = "a" 输出:false 解释:"a" 无法匹配 "aa" 整个字符串。示例 2:
输入:s = "aa", p = "a*" 输出:true 解释:因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。示例 3:
输入:s = "ab", p = ".*" 输出:true 解释:".*" 表示可匹配零个或多个('*')任意字符('.')。提示:
1 <= s.length <= 201 <= p.length <= 20s只包含从a-z的小写字母。p只包含从a-z的小写字母,以及字符.和*。- 保证每次出现字符
*时,前面都匹配到有效的字符
2.题目接口
class Solution {
public:bool isMatch(string s, string p) {}
};3.解题思路及其代码
但是这道题跟第一道题何其相似啊!!!'.'和'?'匹配规则是一样的,但是注意两个题目的'*'的匹配规则是是不一样的。所以在'*"和初始化处就要稍加改造了,改造如下:
初始化:
for(int i = 2;i<n+1;i+=2) if(dp[0][i-2]&&p[i] == '*') dp[0][i] = true;当遇到"*"时填表情况如下:
else if(p[j] == '*'){//按照题意在*前面一定有字符if(p[j-1] == '.')//无敌匹配{dp[i][j] = dp[i][j-2]||dp[i-1][j];}else//不是.{//判断后再匹配if(p[j-1] == s[i]){dp[i][j] = dp[i][j-2]||dp[i-1][j];}else{dp[i][j] = dp[i][j-2];}}解题代码如下:
class Solution { public:bool isMatch(string s, string p) {int m = s.size();int n = p.size();//经典加上空格s = ' '+s;p = ' '+p;//经典二维dp表vector<vector<bool>>dp(m+1,vector<bool>(n+1));dp[0][0] = true;//初始化:当s为空串时for(int i = 2;i<n+1;i+=2) if(dp[0][i-2]&&p[i] == '*') dp[0][i] = true;for(int i = 1;i<m+1;i++){for(int j = 1;j<n+1;j++){//分情况讨论if(p[j] == '.'||s[i] == p[j]){//i,j位置匹配上了就得看dp[i-1][j-1]dp[i][j] = dp[i-1][j-1];}else if(p[j] == '*'){//按照题意在*前面一定有字符if(p[j-1] == '.')//无敌匹配{dp[i][j] = dp[i][j-2]||dp[i-1][j];}else//不是.{//判断后再匹配if(p[j-1] == s[i]){dp[i][j] = dp[i][j-2]||dp[i-1][j];}else{dp[i][j] = dp[i][j-2];}}}}}return dp[m][n];} };
三,交错字符串
1.题目
给定三个字符串
s1、s2、s3,请你帮忙验证s3是否是由s1和s2交错 组成的。两个字符串
s和t交错 的定义与过程如下,其中每个字符串都会被分割成若干 非空 子字符串:
s = s1 + s2 + ... + snt = t1 + t2 + ... + tm|n - m| <= 1- 交错 是
s1 + t1 + s2 + t2 + s3 + t3 + ...或者t1 + s1 + t2 + s2 + t3 + s3 + ...注意:
a + b意味着字符串a和b连接。示例 1:
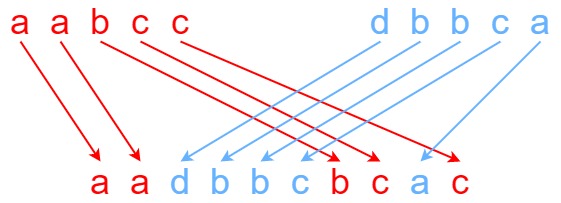
输入:s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac" 输出:true示例 2:
输入:s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc" 输出:false示例 3:
输入:s1 = "", s2 = "", s3 = "" 输出:true提示:
0 <= s1.length, s2.length <= 1000 <= s3.length <= 200s1、s2、和s3都由小写英文字母组成进阶:您能否仅使用
O(s2.length)额外的内存空间来解决它?
2,题目接口
class Solution {
public:bool isInterleave(string s1, string s2, string s3) {}
};3.解题思路及其代码
在看到三个字符串时,我就已经犯蒙了。感觉二维的dp表好像已经解决不了问题了,但是其实是可以解决问题的。解决步骤如下:
1,状态表示
仍然是开一个二维dp表dp[][]。仍然以s1的第i个位置和s2的第j个位置为研究对象研究问题。dp[i][j]表示s1的【1,i]区间和s2的【1,j】区间的字符能不能组成s3的【1,i+j】区间的字符。
2.状态转移方程
在这里我们也是分两种情况来讨论:
1,当s1[i] == s3[i+j]时,dp[i][j] = dp[i-1][j]。
2, 当s2[j] == s3[i+j]时,dp[i][j] = dp[i][j-1]。
3, 当以上两种情况都不成立的话,dp[i][j] = false。
所以dp[i][j] = (s1[i]==s3[i+j]&&dp[i-][j])&&(s2[j] == s3[i+j]&&dp[i][j-1])。
3,初始化
为了让下标对应所以得在每个字符的前面加上" "。
//加上空格,因为空格有意义s1 = " "+s1;s2 = " "+s2;s3 = " "+s3;当s1和s2都是空串时,能够组成空串
//初始化 dp[0][0] = true;当有一个串为空时,另一个串要和s3一一匹配
for(int i =1;i<m+1;i++)//代表s2为空串{if(s1[i] == s3[i]){dp[i][0] = true;}else {break;}}for(int i =1;i<n+1;i++)//代表s1为空串{if(s2[i] == s3[i]){dp[0][i] = true;}else{break;}}4,填表顺序
按照状态转移方程可知填表顺序为:从上到下,从左到右。
5,返回值
返回dp[m][n]
代码如下:
class Solution { public:bool isInterleave(string s1, string s2, string s3) {int m = s1.size();int n = s2.size();if(m+n!=s3.size()) return false;//二维数组表示以i,j位置为结尾能够组成s3的i+jvector<vector<bool>>dp(m+1,vector<bool>(n+1));//加上空格,因为空格有意义s1 = " "+s1;s2 = " "+s2;s3 = " "+s3;//初始化dp[0][0] = true;for(int i =1;i<m+1;i++)//代表s2为空串{if(s1[i] == s3[i]){dp[i][0] = true;}else {break;}}for(int i =1;i<n+1;i++)//代表s1为空串{if(s2[i] == s3[i]){dp[0][i] = true;}else{break;}}//经典以i,j位置为研究对象for(int i = 1;i<m+1;i++){for(int j = 1;j<n+1;j++){dp[i][j] = (s1[i] == s3[i + j] && dp[i - 1][j])|| (s2[j] == s3[i + j] && dp[i][j - 1]);}}return dp[m][n];} };
相关文章:
动态规划学习——通符串匹配,正则表达式
目录 编辑 一,通符串匹配 1.题目 2.题目接口 3,解题思路及其代码 二,正则表达 1.题目 2.题目接口 3.解题思路及其代码 三,交错字符串 1.题目 2,题目接口 3.解题思路及其代码 一,通符串匹配 1…...

【数据开发】Hive 多表join中的条件过滤与指定分区
1、条件过滤 left join 中 on 后面加条件 where 和 and 的区别 1、 on条件是在生成临时表时使用的条件,它不管and中的条件是否为真,都会保留左边表中的全部记录。2、where条件是在临时表生成好后,再对临时表进行过滤的条件。这时已经没有le…...
基于Java SSM框架实现高校人事管理系统项目【项目源码】计算机毕业设计
基于java的SSM框架实现高校人事管理系统演示 JSP技术介绍 JSP技术本身是一种脚本语言,但它的功能是十分强大的,因为它可以使用所有的JAVA类。当它与JavaBeans 类进行结合时,它可以使显示逻辑和内容分开,这就极大的方便了用户的需…...

[C++] 模板进阶(非类型模板参数,特化,分离编译)
文章目录 1、非类型模板参数2、模板的特化2.1 什么是模板特化2.2 函数模板特化2.3 类模板的实例化2.3.1 全特化2.3.2 偏特化 3、模板分离编译3.1 什么是分离编译3.2 模板的分离编译3.3 解决方法 4、模板总结 1、非类型模板参数 模板参数分类类型形参与非类型形参。 类型形参即…...
C++ this指针
通常情况下,类的成员函数都只涉及一个对象,即调用它的对象。但有时候方法可能涉及到两个对象,在这种情况就需要使用到C的this指针。 class Stock { private: ... double total_val; ... public: double total() const {return total_val;} }…...

解决Sortable拖动el-table表头时,由于选择列造成的拖拽顺序错乱的bug
原因 由于我的表头是由数组循环遍历生成的,而选择列不在数组内,只能在循环外定义el-table-column,造成拖动时索引错乱错误代码 <el-tableheader-dragend"headerDragend"id"out-table":data"state.sliceTable&quo…...
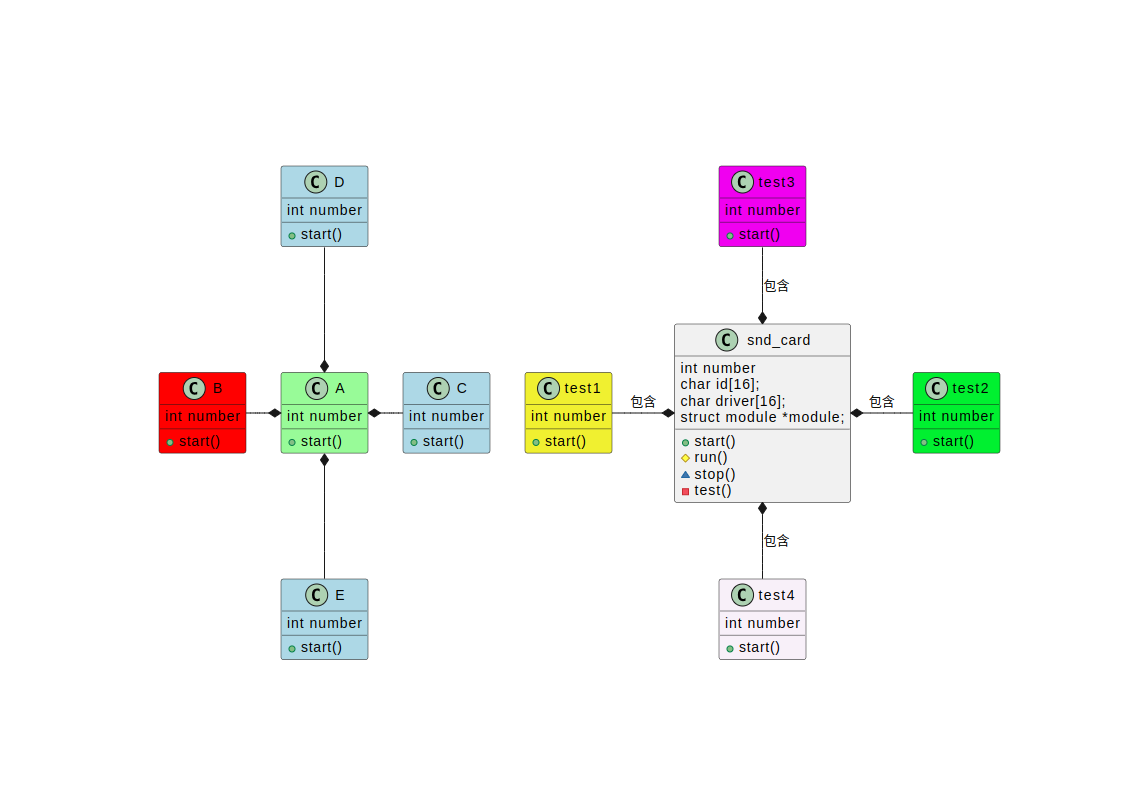
Plantuml之类图语法介绍(十六)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 优质专栏:多媒…...

深入Docker命令行:探索常用命令和实用技巧
Docker命令行界面是每个容器开发者的得力工具。在这篇文章中,将深入探讨一系列常用的Docker命令,以及一些实用技巧,通过更丰富的示例代码,帮助大家更全面地理解和运用Docker命令行工具。 1. Docker基本命令 1.1 镜像操作 深入了…...

qt 容器QVector,QMap,QHash的常见使用与该迭代器的简单介绍
一. QVector容器是一个动态数组,可以容纳任意数量的元素,在相邻的内存中存储给定的数据类型作为一组数据,在QVector前部或中间位置插入元素都会导致内存中大量的数据元素移动,这使得操作速度会减慢.可使用迭代器对这组数据进行访问. 和其他的容器类型类似,QVector…...

两线制无源 4-20mA 回路供电隔离变送器
两线制无源 4-20mA 回路供电隔离变送器 一入一出两线制无源 4-20mA 回路供电隔离变送器 概述:JSD TAW-1001D-100L-F 系列隔离变送器是 4-20mA 两线制回路供电的电流隔离变送配电器,该隔离变送器采用电磁隔离技术,并通过输入端馈电方式,给输入端两线制仪器仪表设备供…...
)
强化学习优质博客记录(随缘更新)
杂记 速成深度强化学习的人可能陷入的几个误区(2023-03更新) DQN DQN表现稳定提升和收敛的技巧集锦 TRPO 如何看懂TRPO里所有的数学推导细节? PPO The 37 Implementation Details of Proximal Policy Optimization强化学习算法中,PPO算法是不是就是加了重要…...
RabbitMQ-hello
0. pom文件 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0"xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0…...
案例044:基于微信小程序的消防隐患在线举报系统
文末获取源码 开发语言:Java 框架:SSM JDK版本:JDK1.8 数据库:mysql 5.7 开发软件:eclipse/myeclipse/idea Maven包:Maven3.5.4 小程序框架:uniapp 小程序开发软件:HBuilder X 小程序…...

MES系统需要具备哪些性能方面的需求?
MES系统需要具备哪些“性能需求”?关于这个问题,我觉得有必要先和大家解释一下,到底什么是性能需求?性能需求在MES系统的作用是什么?讲明白了这2点,问题自然而然就解决了。 什么是性能需求? 通…...

数据在内存中的存储(整型篇)
1.辨析原码反码补码: 1.原码:有32位(int类四个字节,一个字节八个比特位),第一位是符号位,0正1负,其余为二进制位。 2.计算一般是对原码进行计算,但在负数计算使用原码会导…...
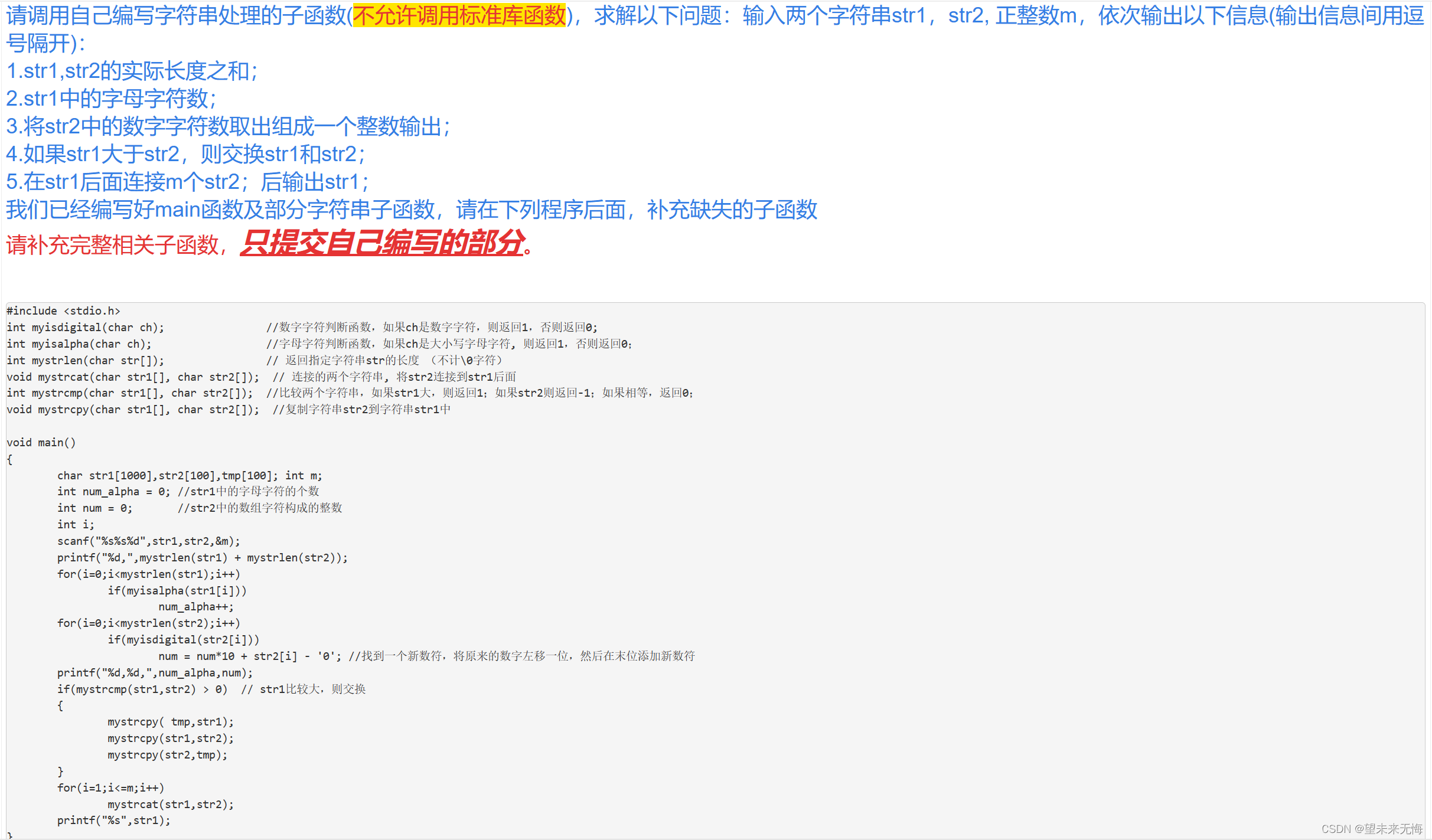
大一作业习题
第一题:答案: #include <stdio.h> void sort(int a[], int m) //将数组a的前m个元素(从小到大)排序 {int i 0;for (i 0; i < m - 1; i){int j 0;int flag 1;for (j 0; j < m - 1 - i; j){if (a[j] > a[j 1]){int t 0;t a[j];…...

Python大模型TensorFlow/PyTorch/Scikit-learn/Keras/OpenCV/Gensim
Python 作为一种高级编程语言,可以用于开发各种大小的模型。以下是一些常见的 Python 大模型,以及它们的优势、劣势和使用场景: TensorFlow: 优势:TensorFlow 是一个非常流行的深度学习库,具有高度的可扩…...

TCP 和 UDP 区别? 2、TCP/IP 协议涉及哪几层架构? 3、描述下 TCP 连接 4 次挥手的过程?为什么要 4 次挥手?
文章目录 1、TCP 和 UDP 区别?2、TCP/IP 协议涉及哪几层架构?3、描述下 TCP 连接 4 次挥手的过程?为什么要 4 次挥手?4、计算机插上电源操作系统做了什么?5、Linux 操作系统设备文件有哪些? 1、TCP 和 UDP …...
pyside/qt03——人机协同的编程教学—直接面向chatGPT实战开发(做中学,事上练)
先大概有个草图框架,一点点丰富 我纠结好久,直接用Python写UI代码 还是用designer做UI 再转Python呢, 因为不管怎么样都要转成Python代码, 想了想还是学一下designer吧,有个中介,有直观理解。 直接这样也可…...
swing快速入门(五)
注释很详细,直接上代码 上一篇 本篇新增内容: 1.布局管理器BorderLayout 2.自适应尺寸方法pack() import java.awt.*; public class swing_test_3 {public static void main(String[] args) {Frame framenew Frame("演示BorderLayout");//…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

Spring AOP代理对象生成原理
代理对象生成的关键类是【AnnotationAwareAspectJAutoProxyCreator】,这个类继承了【BeanPostProcessor】是一个后置处理器 在bean对象生命周期中初始化时执行【org.springframework.beans.factory.config.BeanPostProcessor#postProcessAfterInitialization】方法时…...

用递归算法解锁「子集」问题 —— LeetCode 78题解析
文章目录 一、题目介绍二、递归思路详解:从决策树开始理解三、解法一:二叉决策树 DFS四、解法二:组合式回溯写法(推荐)五、解法对比 递归算法是编程中一种非常强大且常见的思想,它能够优雅地解决很多复杂的…...

渗透实战PortSwigger Labs指南:自定义标签XSS和SVG XSS利用
阻止除自定义标签之外的所有标签 先输入一些标签测试,说是全部标签都被禁了 除了自定义的 自定义<my-tag onmouseoveralert(xss)> <my-tag idx onfocusalert(document.cookie) tabindex1> onfocus 当元素获得焦点时(如通过点击或键盘导航&…...

