算法拾遗二十五之暴力递归到动态规划五
算法拾遗二十七之暴力递归到动态规划七
- 题目一【数组累加和最小的】
- 题目二
- 什么暴力递归可以继续优化
- 暴力递归和动态规划的关系
- 面试题和动态规划的关系
- 如何找到某个问题的动态规划方式
- 面试中设计暴力递归的原则
- 知道了暴力递归的原则 然后设计
- 常见的四种尝试模型
- 如何分析有没有重复解
- 暴力递归到动态规划的套路
- 动态规划的进一步优化
- N皇后问题
题目一【数组累加和最小的】

找较小的集合最接近两个集合总和的一半:
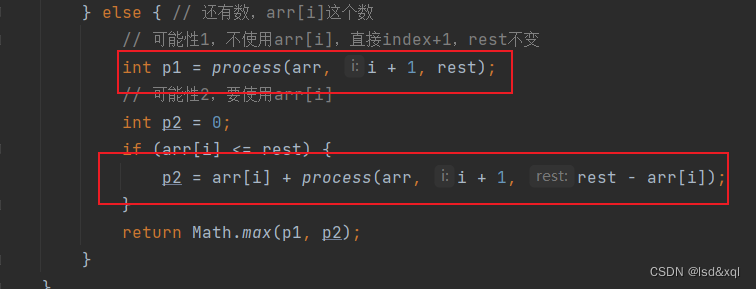
public static int right(int[] arr) {if (arr == null || arr.length < 2) {return 0;}//统计所有数的累加和int sum = 0;for (int num : arr) {sum += num;}return process(arr, 0, sum / 2);}// arr[i...]从i位置出发及其后面的数可以自由选择,// 请返回累加和尽量接近rest,但不能超过rest的情况下,最接近的累加和是多少?public static int process(int[] arr, int i, int rest) {if (i == arr.length) {return 0;} else { // 还有数,arr[i]这个数// 可能性1,不使用arr[i],直接index+1,rest不变int p1 = process(arr, i + 1, rest);// 可能性2,要使用arr[i]int p2 = 0;if (arr[i] <= rest) {p2 = arr[i] + process(arr, i + 1, rest - arr[i]);}return Math.max(p1, p2);}}
改dp,有两个可变参数:
i变化范围为0-N,rest变化范围,从0-sum/2,不会超过此范围。
先看basecase:
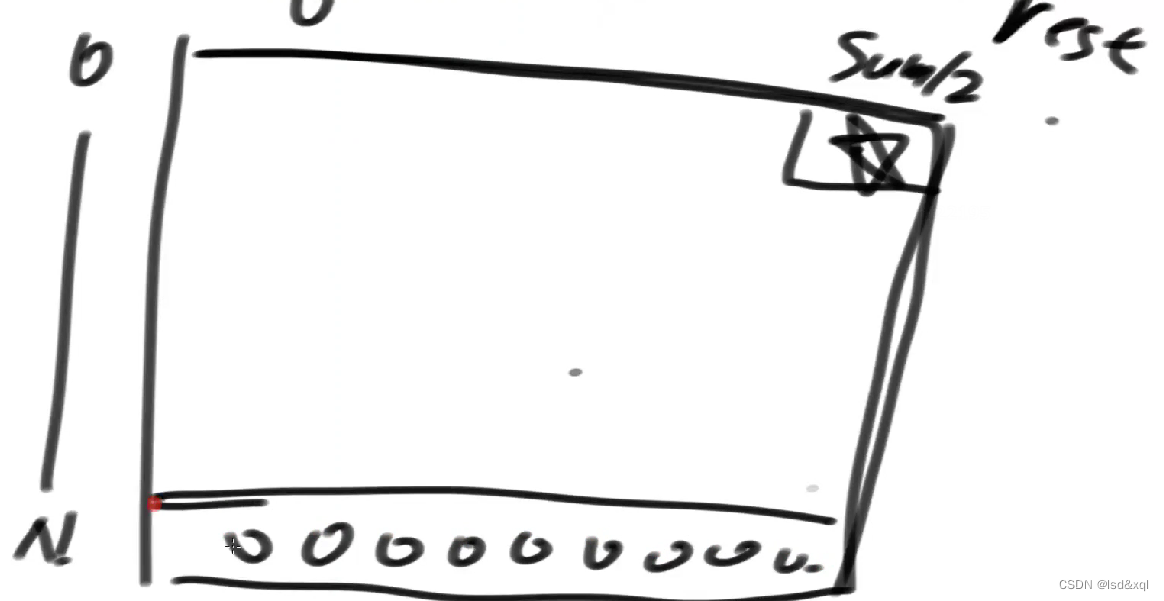
分析普遍位置依赖关系:
i位置依赖于i+1位置
public static int dp1(int[] arr) {if (arr == null || arr.length < 2) {return 0;}int sum = 0;for (int num : arr) {sum += num;}sum /= 2;int N = arr.length;int[][] dp = new int[N + 1][sum + 1];/*int p1 = process(arr, i + 1, rest);// 可能性2,要使用arr[i]int p2 = 0;if (arr[i] <= rest) {p2 = arr[i] + process(arr, i + 1, rest - arr[i]);}*/for (int i = N - 1; i >= 0; i--) {for (int rest = 0; rest <= sum; rest++) {int p1 = dp[i + 1][rest];int p2 = 0;if (arr[i] <= rest) {p2 = arr[i] + dp[i + 1][rest - arr[i]];}dp[i][rest] = Math.max(p1, p2);}}return dp[0][sum];}public static int[] randomArray(int len, int value) {int[] arr = new int[len];for (int i = 0; i < arr.length; i++) {arr[i] = (int) (Math.random() * value);}return arr;}public static void printArray(int[] arr) {for (int num : arr) {System.out.print(num + " ");}System.out.println();}public static void main(String[] args) {int maxLen = 20;int maxValue = 50;int testTime = 10000;System.out.println("测试开始");for (int i = 0; i < testTime; i++) {int len = (int) (Math.random() * maxLen);int[] arr = randomArray(len, maxValue);int ans1 = right(arr);int ans2 = dp1(arr);if (ans1 != ans2) {printArray(arr);System.out.println(ans1);System.out.println(ans2);System.out.println("Oops!");break;}}System.out.println("测试结束");}
题目二

public static int right1(int[] arr) {if (arr == null || arr.length < 2) {return 0;}int sum = 0;for (int num : arr) {sum += num;}if ((arr.length & 1) == 0) {return process1(arr, 0, arr.length / 2, sum / 2);} else {return Math.max(process1(arr, 0, arr.length / 2, sum / 2), process1(arr, 0, arr.length / 2 + 1, sum / 2));}}public static int process1(int[] arr, int i, int picks, int rest) {if (i == arr.length) {//没有数的情况,没法调返回一个-1表示这个过程不能使用return picks == 0 ? 0 : -1;} else {//还有数挑//第一种选择不挑当前数int p1 = process1(arr, i + 1, picks, rest);int p2 = -1;int next = -1;if (arr[i] <= rest) {next = process1(arr, i + 1, picks - 1, rest - arr[i]);}if (next != -1) {//如果后续是有效的才有可能性2p2 = arr[i] + next;}return Math.max(p1,p2);}}
改dp:三个可变参数可用一个三维dp解决
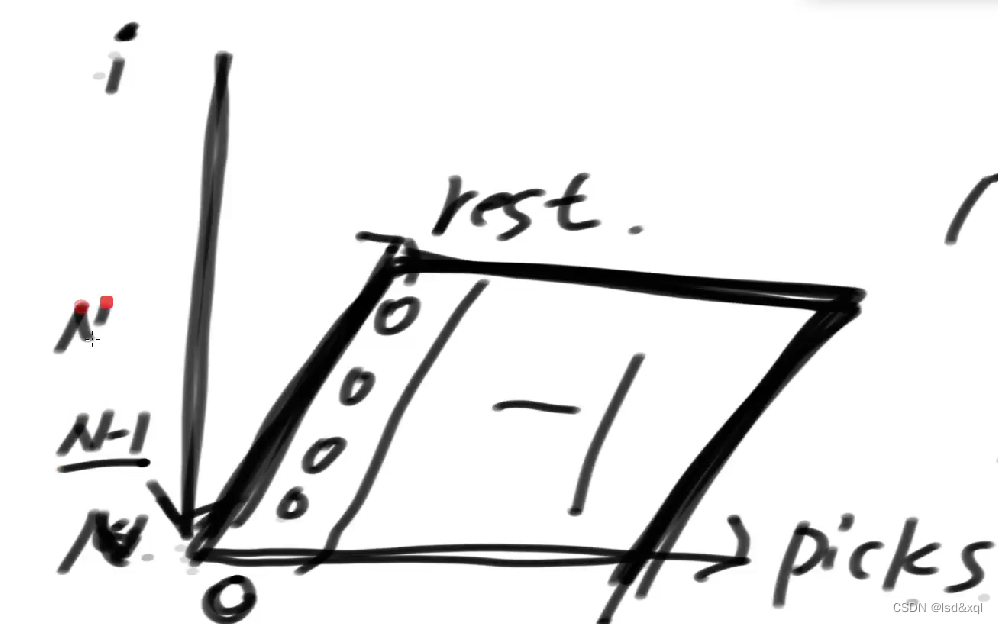
public static int dp4(int[] arr) {if (arr == null || arr.length < 2) {return 0;}int sum = 0;for (int num : arr) {sum += num;}sum /= 2;int N = arr.length;int M = (N + 1) / 2;int[][][] dp = new int[N + 1][M + 1][sum + 1];for (int i = 0; i <= N; i++) {for (int j = 0; j <= M; j++) {for (int k = 0; k <= sum; k++) {dp[i][j][k] = -1;}}}/* if (i == arr.length) {//没有数的情况,没法调返回一个-1表示这个过程不能使用return picks == 0 ? 0 : -1;}*/for (int rest = 0; rest <= sum; rest++) {dp[N][0][rest] = 0;}for (int i = N - 1; i >= 0; i--) {for (int picks = 0; picks <= M; picks++) {for (int rest = 0; rest <= sum; rest++) {/* //还有数挑//第一种选择不挑当前数int p1 = process1(arr, i + 1, picks, rest);int p2 = -1;int next = -1;if (arr[i] <= rest) {next = process1(arr, i + 1, picks - 1, rest - arr[i]);}if (next != -1) {//如果后续是有效的才有可能性2p2 = arr[i] + next;}return Math.max(p1, p2);*/int p1 = dp[i + 1][picks][rest];int p2 = -1;int next = -1;if (picks - 1 >= 0 && arr[i] <= rest) {next = dp[i + 1][picks - 1][rest - arr[i]];}if (next != -1) {p2 = arr[i] + next;}dp[i][picks][rest] = Math.max(p1,p2);}}}if ((arr.length & 1) == 0) {return dp[0][arr.length / 2][sum];} else {return Math.max(dp[0][arr.length / 2][sum], dp[0][(arr.length / 2) + 1][sum]);}}
什么暴力递归可以继续优化


暴力递归和动态规划的关系

面试题和动态规划的关系

如何找到某个问题的动态规划方式

面试中设计暴力递归的原则

知道了暴力递归的原则 然后设计

常见的四种尝试模型

如何分析有没有重复解

暴力递归到动态规划的套路

动态规划的进一步优化

N皇后问题

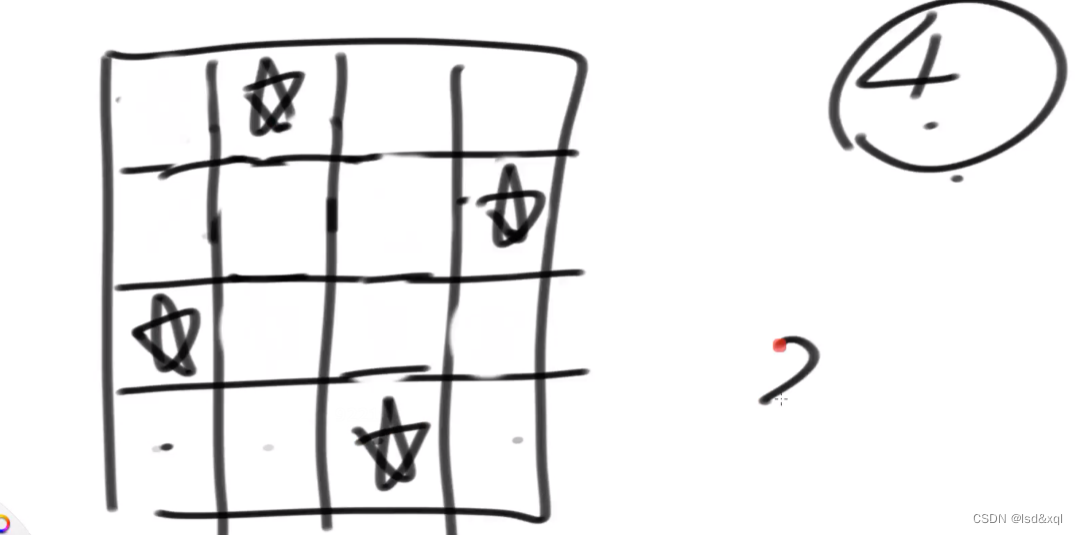
如上算是一种解,考虑皇后的时候一行一行的填入皇后,每一行填入一个皇后,这样就不用检查两个皇后是否共行了。
之前的某个皇后在(x,y),然后当前位置在(甲,乙)位置
如果y==乙或者甲减去x的绝对值等于y-乙的绝对值【共斜线】
复杂度为O(n的n次方)
每一行都有n种决策
public static int num1(int n) {if (n < 1) {return 0;}int[] record = new int[n];return process1(0, record, n);}// 当前来到i行,一共是0~N-1行// 在i行上放皇后,所有列都尝试// 必须要保证跟之前所有的皇后不打架// int[] record record[x] = y 之前的第x行的皇后,放在了y列上,一维数组的列号表示n皇后的行号// 返回:不关心i以上发生了什么,i.... 后续有多少合法的方法数public static int process1(int i, int[] record, int n) {//i来到n位置未发生打架if (i == n) {return 1;}int res = 0;// i行的皇后,放哪一列呢?j列,for (int j = 0; j < n; j++) {if (isValid(record, i, j)) {record[i] = j;res += process1(i + 1, record, n);}}return res;}/*** 判断是否发生打架** @param record* @param i* @param j* @return*/public static boolean isValid(int[] record, int i, int j) {// 0..i-1,检查0->i-1行的皇后是否发生打架for (int k = 0; k < i; k++) {if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {return false;}}return true;}
位运算优化常数时间:
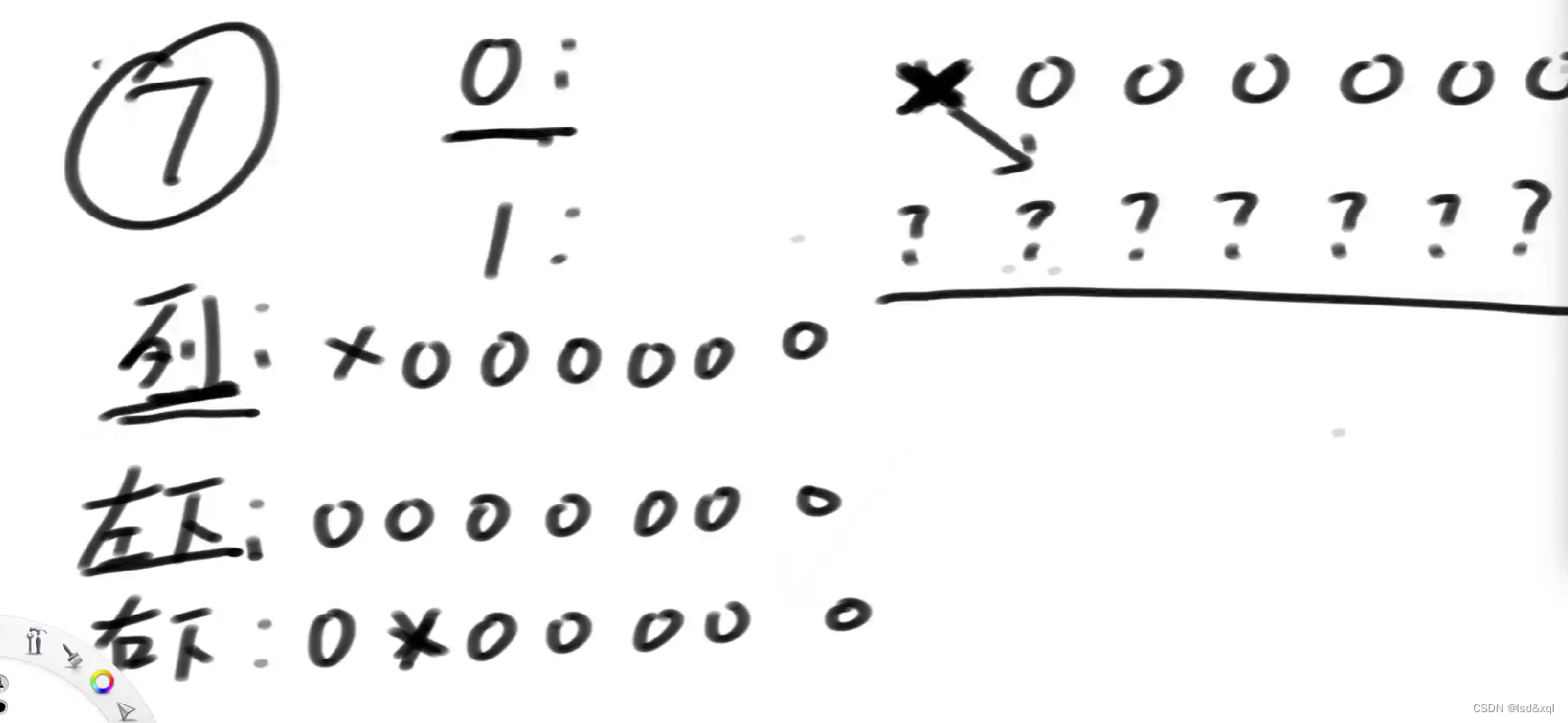
能选的位置是列或上左下与右下还是0的位置。
同理再定义一个第0行的x位置是皇后放置的位置,或出来三个方框的位置是第一行不能选的。
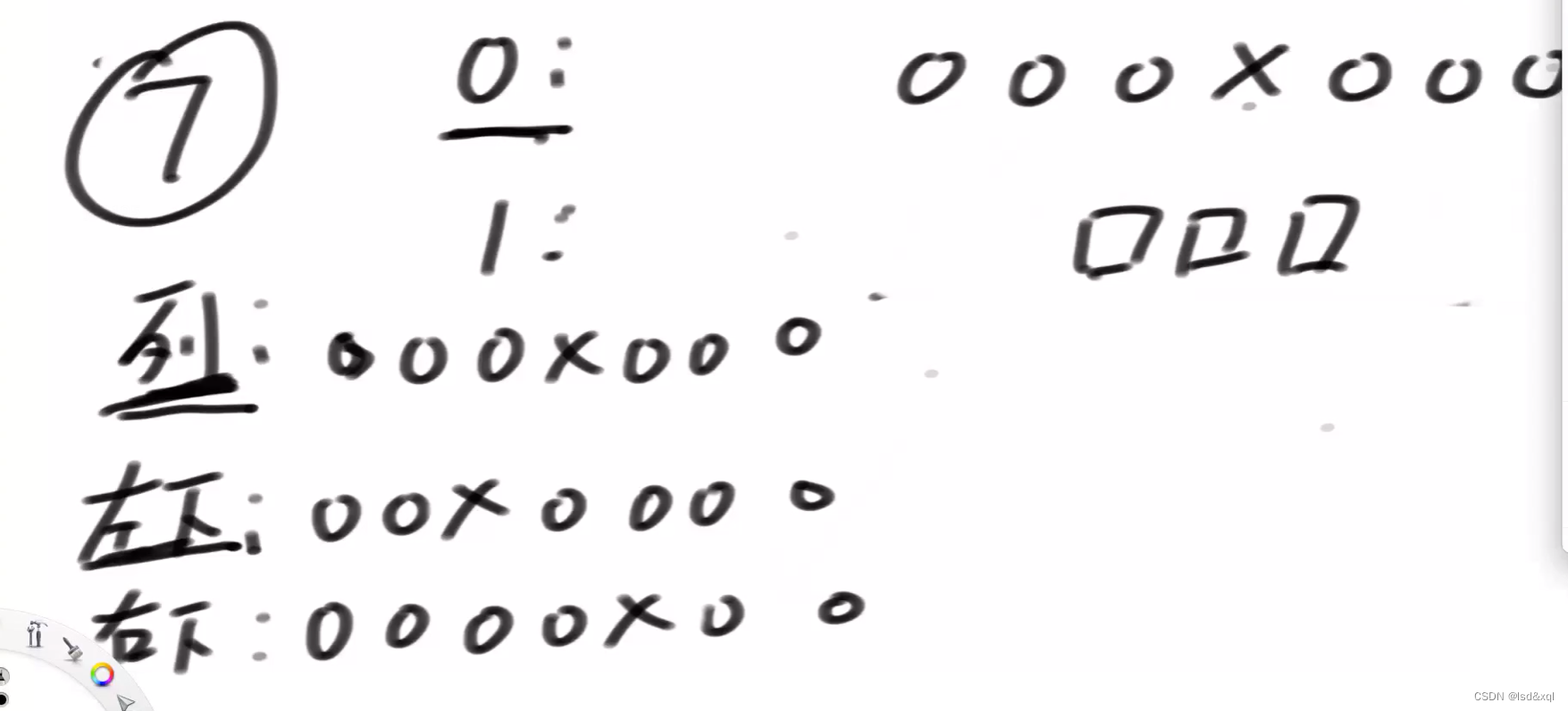
每次放一个皇后都要更新列限制,左下限制以及右下限制。
假设某个时刻是这样的:
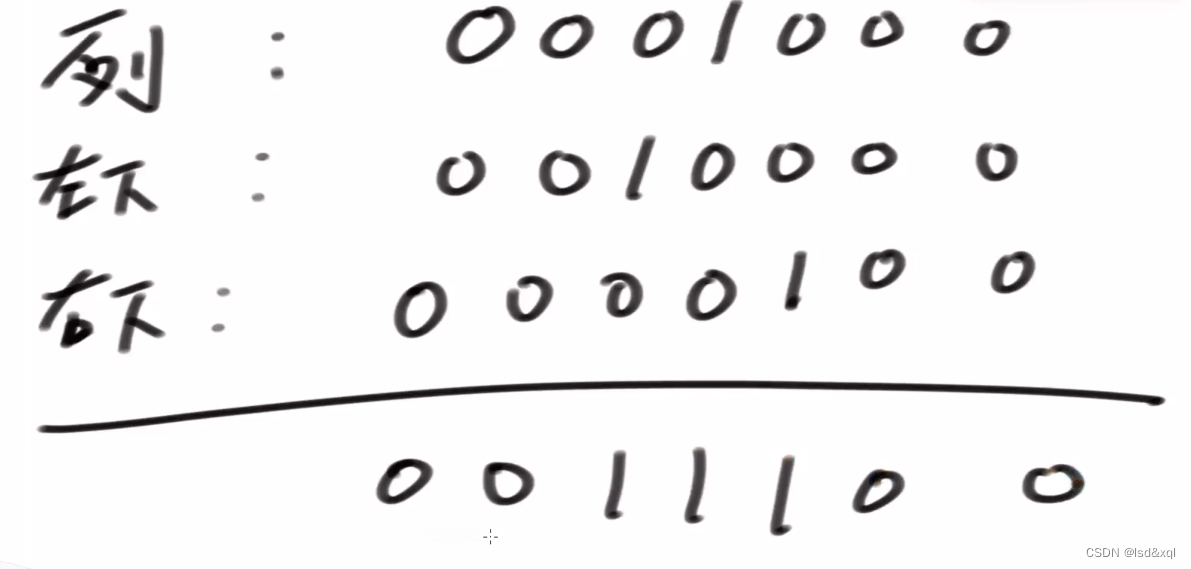
最后是1的不能放皇后是0的可以,然后整体取反变成其他的全1中间的三个1变成三个0
limit是0…011111110…0,然后与一下得到limit=1100011,其中1是能放n皇后的位置
// 请不要超过32皇后问题public static int num2(int n) {if (n < 1 || n > 32) {return 0;}// 如果你是13皇后问题,limit 最右13个1,其他都是0,通过整数的位来标记皇后int limit = n == 32 ? -1 : (1 << n) - 1;return process2(limit, 0, 0, 0);}// 7皇后问题// limit : 0....0 1 1 1 1 1 1 1// 之前皇后的列影响:colLim// 之前皇后的左下对角线影响:leftDiaLim// 之前皇后的右下对角线影响:rightDiaLimpublic static int process2(int limit, int colLim, int leftDiaLim, int rightDiaLim) {//列影响等于了limitif (colLim == limit) {return 1;}// pos中所有是1的位置,是你可以去尝试皇后的位置int pos = limit & (~(colLim | leftDiaLim | rightDiaLim));int mostRightOne = 0;int res = 0;while (pos != 0) {mostRightOne = pos & (~pos + 1);pos = pos - mostRightOne;res += process2(limit, colLim | mostRightOne, (leftDiaLim | mostRightOne) << 1,(rightDiaLim | mostRightOne) >>> 1);//无符号右移}return res;}
相关文章:

算法拾遗二十五之暴力递归到动态规划五
算法拾遗二十七之暴力递归到动态规划七题目一【数组累加和最小的】题目二什么暴力递归可以继续优化暴力递归和动态规划的关系面试题和动态规划的关系如何找到某个问题的动态规划方式面试中设计暴力递归的原则知道了暴力递归的原则 然后设计常见的四种尝试模型如何分析有没有重复…...

Linux进程的创建结束类系统调用总结
tags: Linux OS Syscall C 写在前面 总结一下Linux系统的进程创建/终止/等待等系统调用, 参考: Linux/Unix系统编程手册. 下面主要给出例子, 关于函数原型可以参考书中或者man 2 syscall(例如man 2 fork). 测试环境: Ubuntu 20.04 x86_64 gcc-9 进程创建: fork() 用于创建…...

Git分支的合并策略有哪些?Merge和Rebase有什么区别?关于Merge和Rebase的使用建议
Git分支的合并策略有哪些?Merge和Rebase有什么区别?关于Merge和Rebase的使用建议1. 关于Git的一些基本原理1.1 Git的工作流程原理2. Git的分支合并方式浅析2.1 分支是什么2.2 分支的合并策略2.2.1 Three-way-merge(三向合并原理)2…...
2022-2-23作业
一、通过操作Cortex-A7核,串口输入相应的命令,控制LED灯进行工作 1.例如在串口输入led1on,开饭led1灯点亮 2.例如在串口输入led1off,开饭led1灯熄灭 3.例如在串口输入led2on,开饭led2灯点亮 4.例如在串口输入led2off,开饭led2灯熄灭 5.例如在串口输…...
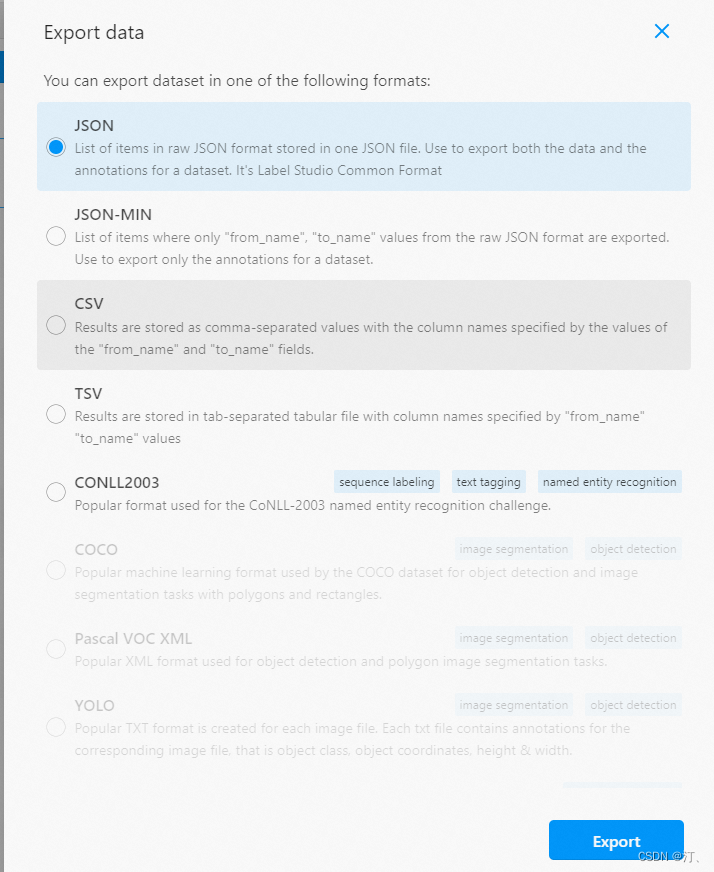
1.基于Label studio的训练数据标注指南:信息抽取(实体关系抽取)、文本分类等
文本抽取任务Label Studio使用指南 1.基于Label studio的训练数据标注指南:信息抽取(实体关系抽取)、文本分类等 2.基于Label studio的训练数据标注指南:(智能文档)文档抽取任务、PDF、表格、图片抽取标注等…...

“高退货率”标签引热议,亚马逊跨境电商是好是坏?
在多数卖家不知情的情况下,亚马逊“高退货率”标签上线,该消息已被官方证实,目的是为了践行以客户为中心的理念和推动卖家提升服务。 官方确认上线“高退货率”标签 近期,有亚马逊卖家发现产品详情页出现了“高退货率”标签&…...

Pinia2
一、入门案例 1、安装 npm i pinia -S 2、注册插件 //main.ts import { createPinia } from pinia app.use(createPinia()) 3、创建store/countStore.ts import { defineStore } from "pinia"; const useCounterStore defineStore(counterStore,{ state(){ return{…...
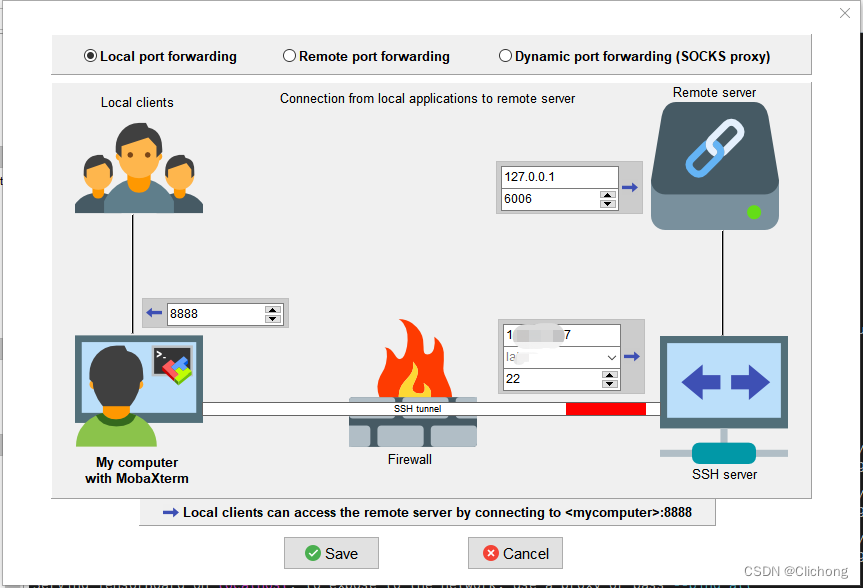
服务器配置 | 在Windows本地打开服务器端Tensorboard结果
文章目录方法1:直接cmd使用ssh登录远程服务器方法2:利用Xshell设置本地端口进行监听方法3:利用MobaXterm设置本地端口监听这里介绍三个方法,在在Windows本地打开服务器端Tensorboard结果 方法1:直接cmd使用ssh登录远程…...
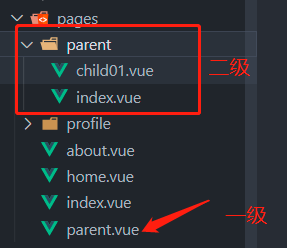
13 nuxt3学习(新建页面 内置组件 assets 路由)
新建页面 Nuxt项目中的页面是在 pages目录 下创建的 在pages目录创建的页面,Nuxt会根据该页面的目录结构和其文件名来自动生成对应的路由。页面路由也称为文件系统路由器(file system router),路由是Nuxt的核心功能之一 方式一…...
)
Linus命令记录(持续编辑版)
目录 一、前言 二、2023年2月查找Linus命令记录 1、竖线 |,双竖线 ||,&和&& 2、wc 3、free 和 top 4、c 库函数 strcpy() 5、c 库函数 memmove() 6、open 三、2023年3月查找Linus命令记录 1、sort 2、uniq 一、前言 有时候遇到不…...
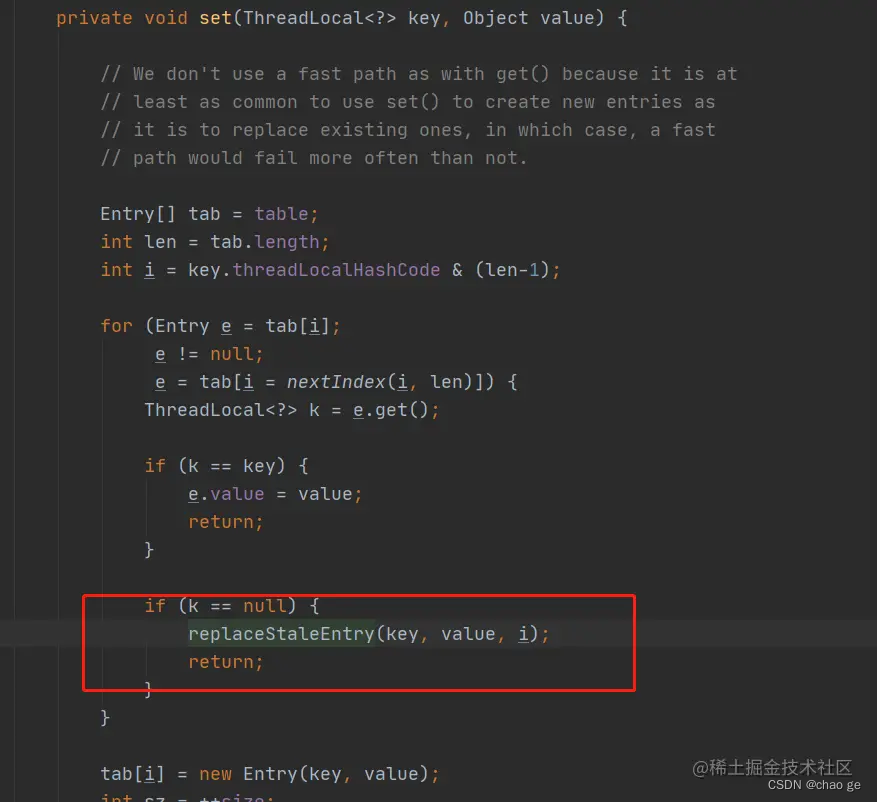
玩转ThreadLocal
前言 ThreadLocal想必都不陌生,当多线程访问同一个共享变量时,就容易出现并发问题,为了保证线程安全,我们需要对共享变量进行同步加锁,但这又带来了性能消耗以及使用者的负担,那么有没有可能当我们创建一个…...

亚马逊二审来袭,跨境电商传统验证算法真的靠谱吗?
多个大卖突遭二审 已有卖家账号被封 近期有不少卖家在论坛上反映称自己收到了亚马逊的二次视频验证邮件。 邮件上称: 卖家必须要完成额外的身份审查,才有资格在亚马逊继续销售商品;亚马逊要求卖家出示注册时提交的身份证原件和营业执照原件…...
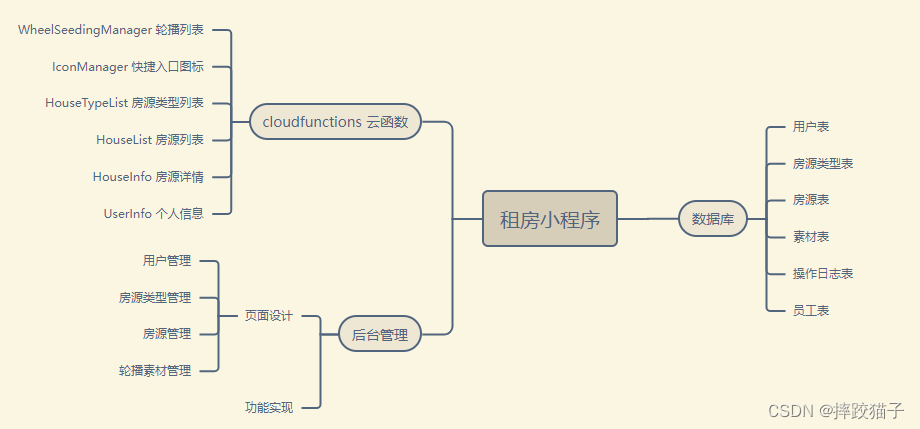
微信小程序|基于小程序+云开发制作一个租房小程序
经济发展的同时伴随着大批人群的流动,租房需求一直是持久不衰的话题,如何租好房,好租房,跟随此文一起制作一个租房小程序,让租房不再困难。 一、小程序1. 创建小程序2. 首页3. 房源列表页4. 房源详情页5. 个人中心页</...

2.4 群辉驱动:多网口,系统网络只能识别两个网口 解决教程
所需工具下载:链接:https://pan.baidu.com/s/1CMLl6waOuW-Ys2gKZx7Jgg?pwdchct提取码:chct安装的黑群晖华硕z490i主板自带一个i225 2.5G,后又插了一个4口8125B四口网卡,发现控制面板->网络->网络界面 只识别了其…...
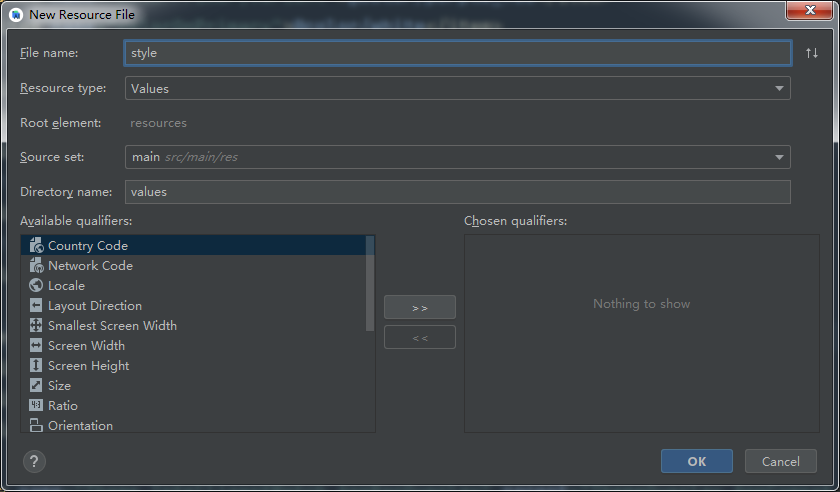
Android正确使用资源res文件
观看此文注意首先有的UI改颜色,没用,发现无法更改按钮背景颜色。我的AS下载的是最新版本,Button按钮的背景颜色一直都是亮紫色,无法更改。为什么呢?首先在你的清单文件中看你应用的是哪个主题。我现在用的是这个可能你…...

5分钟搭建第一个k8s集群
急速上手Minikube搭建单节点 k8s集群实战什么是Minikube?环境准备安装步骤一.安装Docker1.安装yml2.设置阿里云镜像3.查看可安装的docker版本4. 安装docker5. 查看docker版本6.配置docker开机自启动7. 启动docker, 查看docker 启动状态二.安装k8s1.配置镜像源2.安装kubectl3.安…...

【MySQL】查询操作(基础篇)
目录 1、查询操作(Retrieve) 1.1 全列查询 1.2 指定列查询 1.3 查询字段为表达式 1.4 别名 1.5 去重:DISTINCT 1.6 排序:ORDER BY 1.7 条件查询:WHERE 1.8 分页查询 1、查询操作(Retrieve) 查询操作算的上是 SQL 中最复杂的操作了…...

工程管理系统+spring cloud 系统管理+java 系统设置+二次开发
工程项目各模块及其功能点清单 一、系统管理 1、数据字典:实现对数据字典标签的增删改查操作 2、编码管理:实现对系统编码的增删改查操作 3、用户管理:管理和查看用户角色 4、菜单管理:实现对系统菜单的增删改查操…...

MyBatisPlus Study Notes
文章目录1 MyBatisPlus概述1.1 MyBatis介绍1.2 MyBatisPlus特性2 标准数据层开发2.1 MyBatisPlus的CRUD操作API2.2 分页功能接口实现2.2.1 config(配置层)拦截器实现2.2.2 Dao(Mapper)数据访问层(CRUD)操作2.2.3 Junit单元测试进行…...

【Vu3 测试篇】自动化测试
一、为什么需要测试 自动化测试能够预防无意引入的 bug,并鼓励开发者将应用分解为可测试、可维护的函数、模块、类和组件。这能够帮助你和你的团队更快速、自信地构建复杂的 Vue 应用。与任何应用一样,新的 Vue 应用可能会以多种方式崩溃,因…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

路由基础-路由表
本篇将会向读者介绍路由的基本概念。 前言 在一个典型的数据通信网络中,往往存在多个不同的IP网段,数据在不同的IP网段之间交互是需要借助三层设备的,这些设备具备路由能力,能够实现数据的跨网段转发。 路由是数据通信网络中最基…...
