【第38天】不同路径数问题 | 网格 dp 入门
学习指引
- 序、专栏前言
- 一、网格模型
- 二、【例题1】
- 1、题目描述
- 2、解题思路
- 3、模板代码
- 4、代码解析
- 5.原题链接
- 三、【例题2】
- 1、题目描述
- 2、解题思路
- 3、模板代码
- 4、代码解析
- 5.原题链接
- 三、推荐专栏
- 四、课后习题
序、专栏前言
本专栏开启,目的在于帮助大家更好的掌握学习Java,特别是一些Java学习者难以在网上找到系统地算法学习资料帮助自身入门算法,同时对于专栏内的内容有任何疑问都可在文章末尾添加我的微信给你进行一对一的讲解。
但最最主要的还是需要独立思考,对于本专栏的所有内容,能够进行完全掌握,自己完完全全将代码写过一遍,对于算法入门肯定是没有问题的。
算法的学习肯定不能缺少总结,这里我推荐大家可以到高校算法社区将学过的知识进行打卡,以此来进行巩固以及复习。
学好算法的唯一途径那一定是题海战略,大量练习的堆积才能练就一身本领。专栏的任何题目我将会从【题目描述】【解题思路】【模板代码】【代码解析】等四板块进行讲解。
一、网格模型
网格模型是一个很经典的模型,也可以称之为数字三角形模型。其一般形态就是在一个二维的网格中,以左上角为起点,到右下角为终点,只能往下走或者往右走。求得这个过程中可以获取的不同路径数或者权值最大最小问题,当然如何移动也要根据题意来分析,在转移时亦是如此。今天将带来两道最入门的网格dp入门题。
二、【例题1】
1、题目描述
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
2、解题思路
定义 f[i][j]f[i][j]f[i][j] 为走到 iii 行 jjj 列的不同路径数,显然 iii 行 jjj 列只能从i−1i-1i−1 行 jjj 列和iii 行 j−1j-1j−1 列走过来,那么具有转移方程:
f[i][j]=f[i−1][j]+f[i][j−1]f[i][j]=f[i-1][j]+f[i][j-1]f[i][j]=f[i−1][j]+f[i][j−1]
初始化时f[1][1]f[1][1]f[1][1]应该等于1,答案即是f[m][n]f[m][n]f[m][n]
3、模板代码
class Solution {public int uniquePaths(int m, int n) {int[][] f=new int[m+1][n+1];f[1][1]=1;for(int i=1;i<=m;++i){for(int j=1;j<=n;++j){if(i==1&&j==1) continue;f[i][j]=f[i-1][j]+f[i][j-1];}}return f[m][n];}
}
使用滚动数组优化:
class Solution {public int uniquePaths(int m, int n) {int[] f=new int[n+1];f[1]=1;for(int i=1;i<=m;++i){for(int j=1;j<=n;++j){if(i==1&&j==1) continue;f[j]+=f[j-1];}}return f[n];}
}
4、代码解析
滚动数组优化,也是二维dp里常用的优化方式,可以帮忙我们压缩一维空间,不太理解暂时不建议深究。
为了防止边界越界问题,这里大家 iii jjj 都从1开始,如果从0的话在转移时会出现越界。
5.原题链接
不同路径
三、【例题2】
1、题目描述
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
2、解题思路
转移方程和上面是相同的,不同由于存在障碍物,只有在 i,ji,ji,j 不是障碍物时,我们才进去转移才行,同样为了防止边界越界,我们 dp 时下标同样从1开始。
3、模板代码
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int m=obstacleGrid.length;int n=obstacleGrid[0].length;int[][] f=new int[m+1][n+1];if(obstacleGrid[0][0]==0)f[1][1]=1;for(int i=1;i<=m;++i){for(int j=1;j<=n;++j){if(i==1&&j==1) continue;if(obstacleGrid[i-1][j-1]==0)f[i][j]=f[i-1][j]+f[i][j-1];}}return f[m][n];}
}
4、代码解析
注意起点有可能有石头,初始化时需要进行判断。
5.原题链接
不同路径||

三、推荐专栏
四、课后习题
| 序号 | 题目链接 | 难度评级 |
|---|---|---|
| 1 | 最小路径和 | 3 |
相关文章:

【第38天】不同路径数问题 | 网格 dp 入门
本文已收录于专栏🌸《Java入门一百例》🌸学习指引序、专栏前言一、网格模型二、【例题1】1、题目描述2、解题思路3、模板代码4、代码解析5.原题链接三、【例题2】1、题目描述2、解题思路3、模板代码4、代码解析5.原题链接三、推荐专栏四、课后习题序、专…...
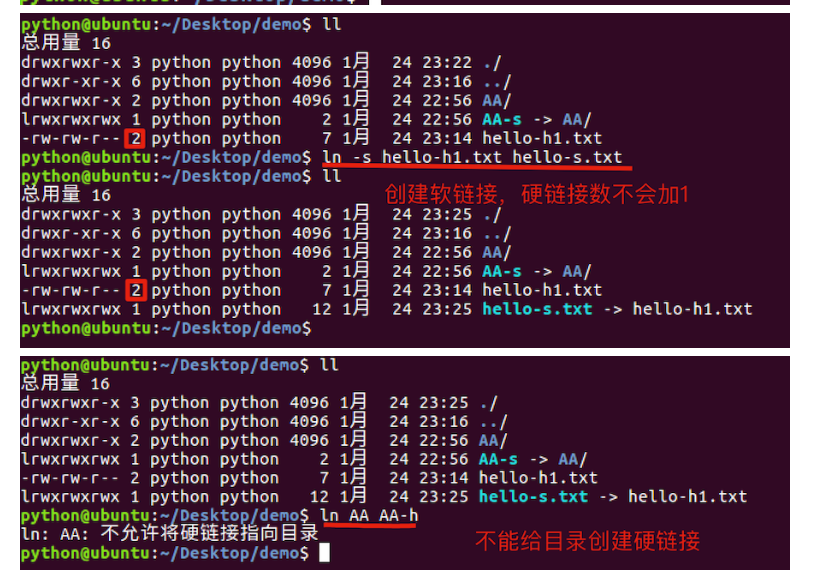
LINUX之链接命令
链接命令学习目标能够说出软链接的创建方式能够说出硬链接的创建方式1. 链接命令的介绍链接命令是创建链接文件,链接文件分为:软链接硬链接命令说明ln -s创建软链接ln创建硬链接2. 软链接类似于Windows下的快捷方式,当一个源文件的目录层级比较深&#x…...

1628_MIT 6.828 xv6_chapter0操作系统接口
全部学习汇总: GreyZhang/g_unix: some basic learning about unix operating system. (github.com) 这本书最初看名字以为是对早期unix的一个解读,但是看了开篇发现 不完全是,只是针对JOS教学OS系统来做的一些讲解。 Xv6是对UNIX v6的重新实…...

使用 Sahi 实现 Web 自动化测试
Sahi 是 Tyto Software 旗下的一个基于业务的开源 Web 应用自动化测试工具。Sahi 运行为一个代理服务器,并通过注入 JavaScript 来访问 Web 页面中的元素。Sahi 支持 HTTPS 并且独立于 Web 站点,简单小巧却功能强大。它相对于 Selenium 等自动化测试工具…...

天津菲图尼克科技携洁净及无菌防护服解决方案与您相约2023生物发酵展
BIO CHINA 生物发酵产业一年一度行业盛会,由中国生物发酵产业协会主办,上海信世展览服务有限公司承办,2023第10届国际生物发酵产品与技术装备展览会(济南)于2023年3月30-4月1日在山东国际会展中心(济南市槐…...
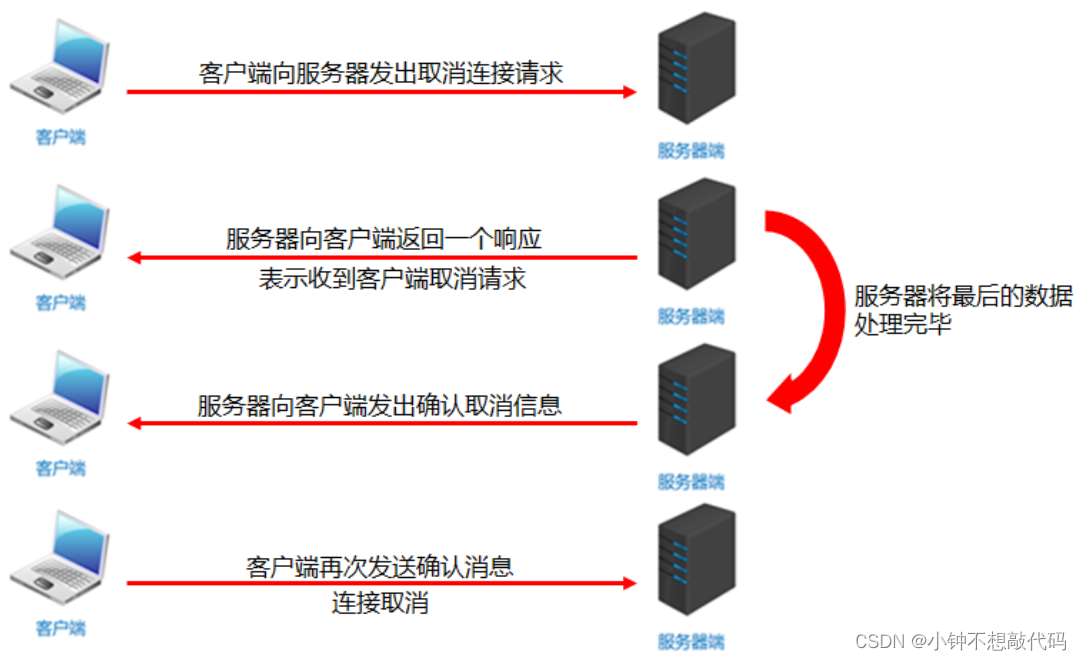
Java 网络编程详解
1、什么是网络编程 在网络通信协议下,不同计算机上运行的程序,可以进行数据传输。 应用场景: 1、即时通信 2、网游对战 3、邮件等等 Java中可以使用java.net包下的技术轻松开发出常见的网络应用程序 2、网络编程三要素 2.1 IP地址 要…...

Scratch少儿编程案例-几何形式贪吃蛇
专栏分享 点击跳转=>Unity3D特效百例点击跳转=>案例项目实战源码点击跳转=>游戏脚本-辅助自动化点击跳转=>Android控件全解手册点击跳转=>Scratch编程案例👉关于作者...

一定要收藏的面试思维导图,粉丝分享面试经验
一位粉丝分享面试经验:1.常见面试题有哪些?主要从以下一些知识点做了准备: 常用的分析方法、Excel、SQL、 A/B测试、产品分析。然后每份面试针对职位要求,还有前期和HR聊天一点点了解这个职位之后,定向准备。 Excel、S…...
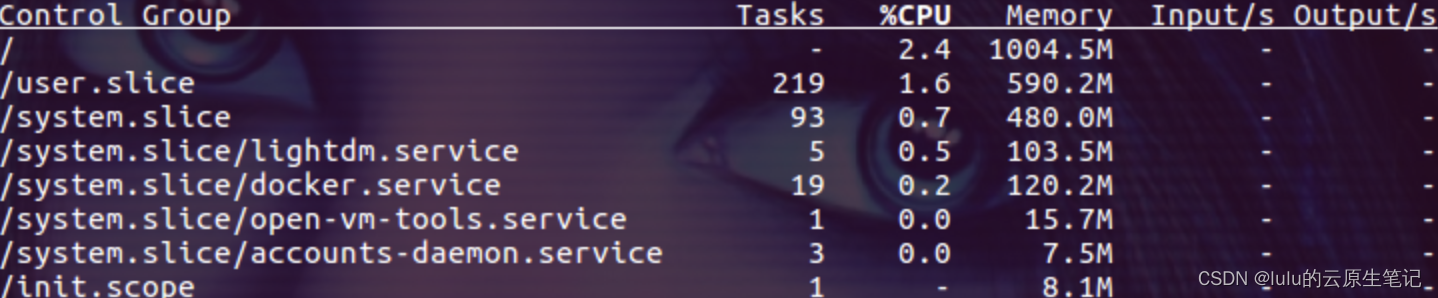
【博客615】通过systemd设置cgroup来限制服务资源争抢
通过systemd设置cgroup来限制服务资源争抢 1、场景 我们的宿主机上通常会用systemctl来管理一些agent服务,此时我们需要限制服务的cpu,memory等资源用量,以防止服务之前互相争抢资源,导致某些核心agent运行异常 2、systemd与cgro…...
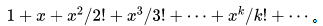
C语言经典编程题100例(21-40)
21、练习3-2 计算符号函数的值对于任一整数n,符号函数sign(n)的定义如下:请编写程序计算该函数对任一输入整数的值。输入格式:输入在一行中给出整数n。输出格式:在一行中按照格式“sign(n) 函数值”输出该整数n对应的函数值。输入样例1:10输出样例1:sig…...
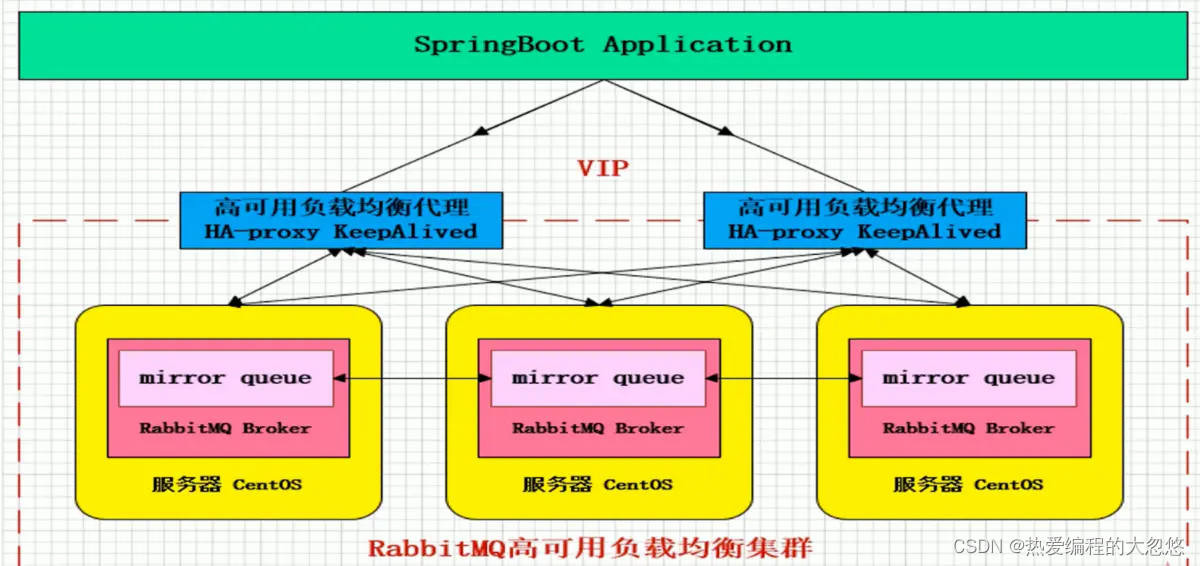
Rabbitmq业务难点
Rabbitmq业务难点1.消息生产者发送的消息无法路由到任何一个队列怎么处理?2.聊聊Rabbitmq的七种工作模式3.Rabbitmq的消息确认机制4.Rabbitmq的消息持久化5.发布确认模式如何确保生产者能够成功将消息投递到消息队列6. Rabbitmq基于队列设置消息过期时间和单独针对消息设置过期…...

服务器如何下载百度网盘文件?Linux服务器如何在百度网盘中连接、上传下载;在Linux服务器上下载百度云盘中的资料
前言 百度云提供Python包bypy进行远程服务器的对接然后下载: https://github.com/houtianze/bypy 可以通过pip直接下载,授权本人的百度云账号后,就可以直接使Linux电脑本地文件与百度网盘的apps(我的应用数据)/bypy目…...

Cesium-数字仿真-你总要了解
Cesium(专注于时空数据的实时可视化) cesium是一款三维地球开源框架(可以多平台、跨平台使用)cesium隶属于美国AGI公司(Analytical Graphics Incorporation),美国通用公司宇航部的工程师创始开源 周边产…...

原型、原型链、__proto__与prototype的区别、继承
一.什么是原型与原型链 根据MDN官方解释: JavaScript 常被描述为一种基于原型的语言——每个对象拥有一个原型对象[[Prototype]] ,对象以其原型为模板、从原型继承方法和属性。原型对象也可能拥有原型,并从中继承方法和属性,一层一层、以此类…...

前端 面经
1说一说cookie sessionStorage localStorage 区别?解题思路得分点 数据存储位置、生命周期、存储大小、写入方式、数据共享、发送请求时是否携带、应用场景 标准回答 Cookie、SessionStorage、 LocalStorage都是浏览器的本地存储。 它们的共同点:都是存储…...

[oeasy]python0080_设置RGB颜色_24bit_24位真彩色_颜色设置
RGB颜色 回忆上次内容 上次 首先了解了 索引颜色 \33[38;5;XXXm 设置 前景为索引色\33[48;5;XXXm 设置 背景为索引色 RGB每种颜色 可选0-5总共 6 级 想用 精确RGB值 真实地 大红色画个 大红桃心 ♥️ 有可能吗??🤔 rgb 模式 关于 RGB 模式…...
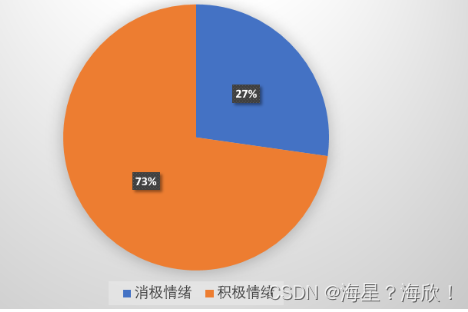
实战项目-用户评论数据情绪分析
目录1、基于词典的方法2、基于词袋或 Word2Vec 的方法2.1 词袋模型2.2 Word2Vec3、案例:用户评论情绪分析3.1 数据读取3.2 语料库分词处理3.3 Word2Vec 处理3.4 训练情绪分类模型3.5 对评论数据进行情绪判断目的:去判断一段文本、评论的情绪偏向在这里&a…...
文本编辑快捷键 发展史)
day02 DOS(续)文本编辑快捷键 发展史
day02课堂笔记 1、常用的DOS命令(续) 1.1、del命令,删除一个或者多个文件 删除T1.class文件 C:\Users\Administrator>del T1.class 删除所有.class结尾的文件,支持模糊匹配 C:\Users\Administrator>del *.class T1.classT1…...

arm64与aarch64
结论: 目前arm64和aarch64概念已合并,新版64位arm程序统称aarch64. 问题引入: 存在部分机器,安装arm版本ss,会报错,提示 rootlocalhost ~]# rpm -ivh senseshiel50 59130arm64.rpm Verifying... ########…...

QString详解
QString存储16位Qchar(Unicode)字符串 QString使用隐式共享(copy-on-write)来提高性能。 什么是Unicode? unicode是一种国际标准,支持当今使用的大多数操作系统,他是US-ASCII和Latin-1的超集(与子集相同字符编码相同…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
